文章编号: 1004-0609(2006)10-1689-09
异常晶粒长大的Monte Carlo模拟
张继祥1, 2, 关小军2
(1. 重庆交通大学 机电与汽车工程学院, 重庆 400074;
2. 山东大学 材料科学与工程学院, 济南 250061)
摘 要: 采用作者提出的Monte Carlo Potts新模型, 模拟研究了高纯铝在各向异性晶界能和晶界迁移率条件下晶粒长大的组织、 动力学和晶粒尺寸分布特征, 揭示初始组织织构强度对异常晶粒长大的影响规律。 结果表明: 各向异性晶界能和晶界迁移率使晶粒尺寸不均匀、 形状不规则, 降低了晶粒长大指数, 晶粒尺寸分布偏离对数正态分布; 异常晶粒长大只出现在中等强度的织构组织中, 而不会在太强或太弱织构组织中出现。 理论分析认为各向异性晶界能和晶界迁移率是异常晶粒长大的内因, 织构是引起异常晶粒长大的外因, 其强度决定了异常晶粒长大是否出现。
关键词: 异常晶粒; Monte Carlo; 模拟; 织构
中图分类号: TG111; O189 文献标识码: A
Simulation of abnormal grain growth by Monte Carlo
ZHANG Ji-xiang1, 2, GUAN Xiao-jun2
(1. School of Machine and Electronic,
Chongqing Jiaotong University, Chongqing 400074, China;
2. School of Materials Science and Engineering, Shandong University, Jinan 250061, China)
Abstract: Some grain growth behaviors of hign-pure Al, such as microstructure, kinetics, grain size distribution, etc were investigated on condition of anisotropic grain boundary energy and mobility, and the effect law of texture in microstructure on abnormal grain growth was revealed by a Modified Monte Carlo Potts model. The results show that the anisotropy of grain boundary energy and mobility induce grain size inhomogeneous, grain shape irregular, grain growth exponent decreasing, grain size distribution deviating from log-normal distribution. Abnormal grain growth occurs only in the microstructure with middle class intensity texture, but not in the microstructure with too high class or too low class intensity texture. Theoretical analysis shows that the anisotropic grain boundary energy and mobility are intrinsic factors that cause abnormal grain growth, and the texture is external factor whose intensity determines whether the abnormal grain growth appears.
Key words: abnormal grain; Monte Carlo; simulation; texture
正常晶粒长大是指晶粒尺寸保持相对均匀, 晶粒形状保持相对稳定, 平均晶粒尺寸平稳增加的晶粒长大过程; 异常晶粒长大是指组织中大部分晶粒的生长由于某种原因受阻, 只有极少数晶粒长大, 或者组织中大部分晶粒长大速度较慢, 而极少数晶粒在局部区域快速长大的现象[1]。 异常晶粒长大与正常晶粒长大的区别为: 极少数晶粒长大速度明显比基体晶粒快; 组织中最大晶粒直径Db与晶粒平均直径Dm的比值Db/Dm>2.5, 且Db/Dm随时间逐渐增大; 晶粒尺寸分布F(D/Dm)是非稳态的, 偏离对数正态分布。
实验研究发现, 引起基体晶粒异常长大的外部因素有: 薄试件中的晶粒表面能[2], 弥散分布的第二相粒子[3, 4], 组织织构[5-7]。 较多实验中发现了异常长大行为, 如Simpson等[8]提出金属冷变形织构诱导异常晶粒长大的观点; 舒龙卫等[9]在铝箔退火过程发现了异常晶粒长大现象, Park等[10]和Tomida等[11]分别在硅钢中发现织构引起异常晶粒长大现象, Stout等[12]在FeAl金属间化合物中也发现了织构引起的异常晶粒长大现象。 然而, 织构对异常晶粒长大的影响机理尚没有完全被揭示。
Monte Carlo Potts模型(以下简称MC Potts模型)是一种离散的、 基于概率统计理论的数值模拟模型, 它可以模拟退火再结晶和晶粒长大的所有特征, 而且在复杂组织(如具有织构、 二相粒子的组织)模拟方面具有其它模型无法比拟的优势, 因此, MC Potts模型逐渐成为组织模拟的首选模型。 美国Exxon 研究小组提出了再结晶、 晶粒长大MC Potts模型(简称Exxon模型)[13-17], 美国橡树岭国家实验室、 森地亚国家实验室、 德国以Raabe为首的研究组等分别采用Monte Carlo方法对再结晶、 晶粒长大等领域开展广泛的研究[18, 19]。 国内北京科技大学、 山东大学、 中科院金属所等已开始研究, 但研究领域和研究深度相对不够, 在异常晶粒长大方面的研究还是空白。 本文拟采用作者提出的改进MC Potts模型, 研究异常晶粒长大行为、 分析异常晶粒长大影响因素, 揭示织构对异常晶粒长大的影响机理。
1 模型的建立
1.1 体系点阵结构及初始微观状态
将组织对象离散成三角形网格体系, 总结点数为N, 每个结点代表组织的一个面积单元。 对体系中所有结点随机赋予一个正整数Si(1≤Si≤Q, Q为系统状态数, 这里指最大取向数, Q>2), 代表该结点所在晶粒的晶体学取向。 一个晶粒可看成取向数相同的相邻结点的集合; 晶界认为处于不同取向数的邻近结点之间。
经过赋值后的体系作为MC模拟的初始微观状态x0, 可描述为
1.2 结点取向数定义
为了便于晶界特征的精确描述, 本文将取向数与二维晶粒取向进行了对应, 让每一个取向数都指向实际的晶粒取向。 方法如下: 在直角坐标系中, 处于二维平面内的晶粒有0~360°的取向, 因为晶粒取向的特殊性, 一个晶粒取向与反向取向认为是相同的取向, 因此, 可以用0~180°描述二维空间的所有晶粒取向。 将0~180°取向均匀离散成180个取向, 并用180个取向数表示, 每个取向数代表一个对应的晶体取向, 例如1代表1°, 2代表2°,..., 180代表180°等, 如图1所示。
由以上取向数的物理定义, 晶界两侧晶粒G1、 G2取向差ΔθG2G1的计算公式为
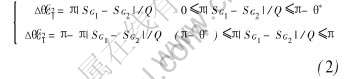
式中 SG1, SG2分别为晶界两侧晶粒G1, G2内结点的取向数; Q为总取向数; θ*为小角度晶界极限。
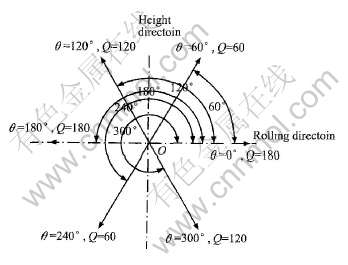
图1 取向数Q与二维晶粒取向的对应关系
Fig.1 Relation of orientation number Q and 2D grain orientation
1.3 能量Hamilton函数
晶粒长大的驱动力来源于晶界能, MC模型中将晶界能离散到结点上, 结点能量形式为
式中 n为结点i邻近结点数(n=6); Sj为结点i的第j个邻近结点的取向数; δSiSj为Kronecker符号; Jji为结点i的第j个邻近结点之间晶界能。 本文将晶界能Jji与晶粒间取向差Δθji相关性称为晶界能各向异性, 用Read-Shockley公式描述为[20]
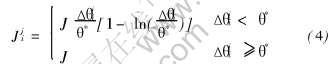
式中 Δθji为结点i的第j个邻近结点之间的取向差; Δθ*为小角度晶界极限, 本文取15°; J为大角度晶界晶界能, J/m2。
1.4 微观状态Markov链的构建
任选体系中一结点i, 尝试将其取向数Si改变为S′i, 得到一新的微观组织状态x1; 再随机选取另一结点, 尝试改变取向数, 得到另一新的微观组织状态x2; 重复以上步骤, 将产生一系列微观状态x1, x2, …, xM。 Markov过程规定每一步所达到的微观状态xs只与前一微观状态xr有关, 从该微观状态xr到下一微观状态xs的转换概率为w(xr→xs)。
1.5 结点再取向时新取向数S′i的选择方法
根据作者提出的“择优转换原则”[21], S′i选择使体系能量降幅最大的近邻结点的取向数。 结点“择优转换原则”物理本质是促使结点附近的晶界朝其曲率中心移动。
1.6 转换概率w(xr→xs)
基于晶界迁移Turnbull线性速率方程, 作者提出了新的结点概率转换公式[22], 其形式为
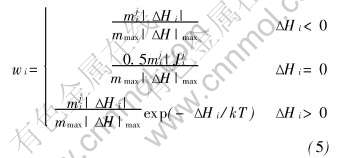
式中 mji为结点i和第j个邻近结点之间晶界的迁移率, m4/(s·J); mmax为在1MCs内体系中所有结点取向转换晶界迁移最大的晶界迁移率, m4/(s·J)(MCs为体系完成的一个MC模拟步); |ΔHi|为结点i取向转变前后的能量差, 是晶界迁移的驱动力, J/m3; |ΔH|max为体系中所有结点的最大晶界能, J/m3。
本文将晶界迁移率mji与取向差Δθji相关性称为晶界迁移率各向异性, 用Humphreys经验模型描述为[23]
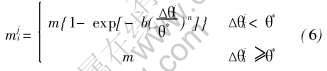
式中 常数b=5, n=4; m为大角度晶界迁移率, m4/(s·J)。
1.7 微观组织的演化
随机选取体系中一结点, 尝试改变其取向数, 得到一新的微观状态x1; 再随机选取另一结点, 尝试改变其取向数, 得到另一新的微观状态x2; 重复以上步骤, 将产生一系列微观状态x1, x2, …, xM, 系统的状态由初始微观状态出发转移向平衡状态靠拢。
每随机选取N次并按上述Markov过程进行微观状态转变后, 体系完成了一个MC模拟步(MCs), 每一个MC模拟步后的微观状态用xnN表示。
2 模拟条件
为了简化模型, 本文假设模拟初始组织是单一织构组织。 初始织构组织的生成方法是: ①将代表晶粒取向的结点取向数S集束到一取向数μ附近, 并使其呈正态分布; ②将按正态分布的取向数随机地赋予体系结点。 正态分布函数为
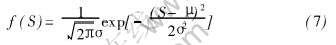
式中 σ, μ为正态分布函数的参数, σ>0; σ越大, 分布越分散, 表示织构越弱; σ越小, 分布越集中, 表示织构越强。
设织构类型为铝再结晶立方织构{001}〈100〉; 织构强度分别采用σ=2.5, 7.5, 15, 25, 40, 60, 90, 180; 晶界能γ=0.324J/m2, 扩散常数D0=1.71×10-4 m/s, 扩散激活能Qm=1.089×10-9 J, 模拟温度为T=573K; 最大取向数Q=180; 点阵常数dMC=5×10-6 m。
3 模拟结果与讨论
3.1 各向异性对晶粒长大特征的影响
3.1.1 组织演变
图2所示为采用各向异性条件模拟的组织形貌。 与文献[21]模拟结果对比可知: 由于采用了各向异性条件, 组织中出现较多形状不规则、 非等轴晶; 三晶界交角偏离120°; 除少部分大晶界边数大于6之外, 大部分晶界边数小于或等于5; 晶粒尺寸不均匀, 出现了部分相对较大晶粒。
3.1.2 晶粒长大动力学
图3所示为模拟的晶粒长大动力学曲线及其对数分析曲线。 可以看出, 在各向异性晶界能和迁移率条件下, 晶粒长大速度低于各向同性条件的速度; 晶粒长大指数nbe=0.36, 小于各向同性条件下模拟结果0.47, 也远远低于理论值。 以上结果说明, 各向异性晶界能和迁移率阻碍晶粒长大, 降低了nbe值。
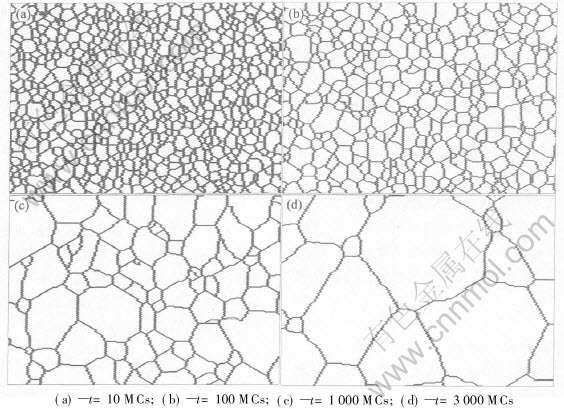
图2 各向异性晶界能和迁移率条件下模拟的晶粒长大微观组织演变
Fig.2 Microstructures evolution in grain growth with anisotropic grain boundary energy and mobility
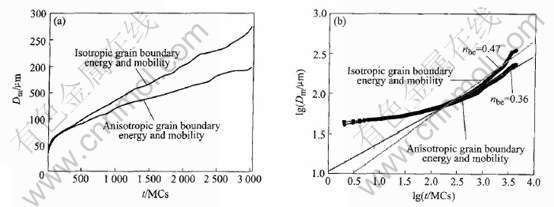
图3 各向异性晶界能和迁移率条件下的晶粒长大动力学曲线及其对数分析曲线
Fig.3 Curves of grain growth kinetics (a)and logarithm analysis (b) with anisotropic grain boundary energy and mobility
3.1.3 晶粒尺寸分布
图4所示为各向异性晶界能和迁移率条件下模拟的晶粒长大过程晶粒尺寸分布的演变。 可以看出: 随模拟时间增加, 晶粒尺寸分布明显地偏离对数正态分布, 卡方差x2变大, μ值降低, 峰值点左移; 分布曲线没有相似性, 随模拟时间增加, σ增大, 尺寸分布范围变宽; 某些组织内最大晶粒直径与平均晶粒直径比值Db/Dm大于2.5。
总之, 在各向异性晶界能和迁移率条件下, 组织中晶粒尺寸趋于非均匀、 形状趋于不规则; 晶粒长大速度慢于各向同性条件的晶粒长大速度, 晶粒长大指数小于各向同性下的晶粒长大指数, 远小于理论值0.5; 晶粒尺寸分布逐渐偏离对数正态分布; 晶粒尺寸分布范围变宽, 分布曲线不具备相似性。以上模拟结果说明, 采用各向异性条件使模拟的组织特征偏离正常晶粒长大特征。
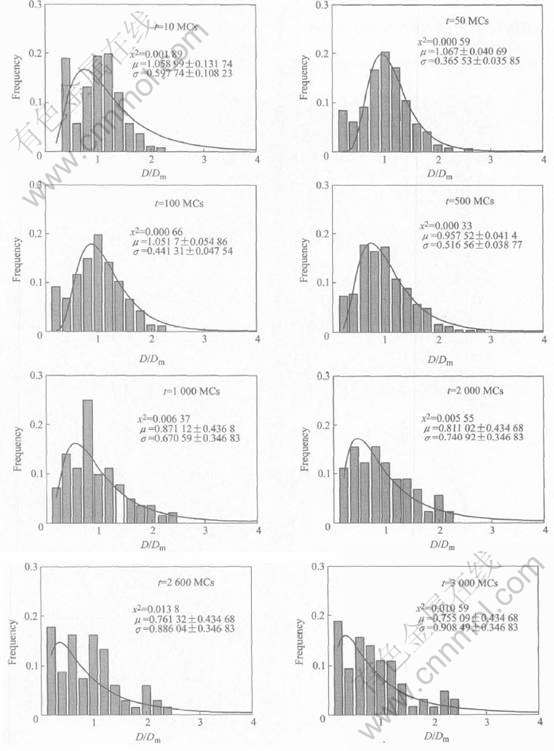
图4 各向异性晶界能和迁移率条件下模拟的晶粒尺寸分布演变
Fig.4 Simulated grain size distribution evolution with anisotropic grain boundary energy and mobility
3.2 初始组织织构强度对晶粒长大特征的影响
3.2.1 微观组织特征
图5所示为有织构初始组织模拟的晶粒长大组织。 可以看出: 初始组织织构越强, 平均晶粒度越小, 说明织构影响了晶粒长大; 在较强织构组织或较弱组织内, 晶粒尺寸相对均匀, 而在中等强度织构组织中(25≤σ≤60), 晶粒尺寸不均匀, 出现了异常长大的晶粒。
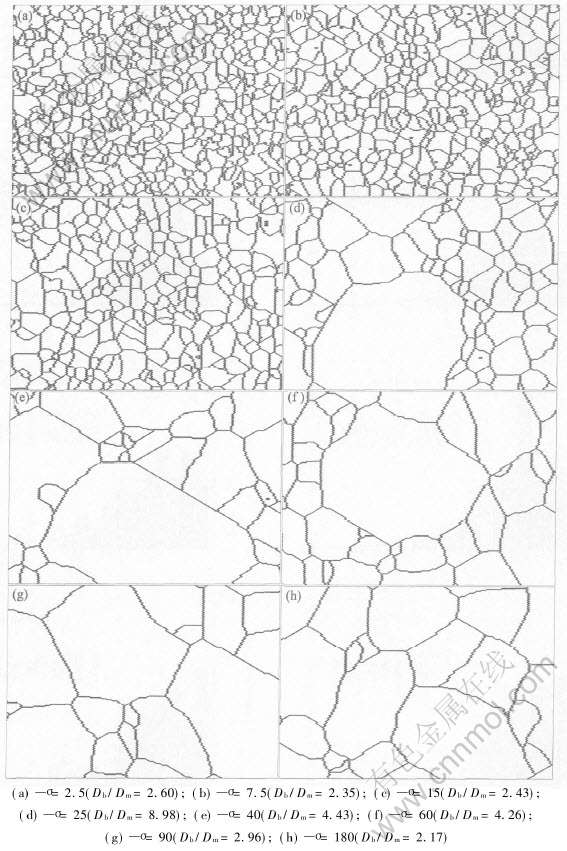
图5 织构强度对异常晶粒长大影响的模拟组织
Fig.5 Simulated microstructures describing effects of texture intensities on abnormal grain growth(tMC=3000MCs)
虽然人们在实验中经常看到织构材料的异常晶粒长大过程, 但从以上模拟结果来看, 并不是所有织构材料中都会出现异常晶粒长大。 下面研究Db/Dm的变化规律可进一步揭示织构强度对异常晶粒长大的影响规律。
3.2.2 Db/Dm的变化规律
从图6模拟结果来看, 在所有织构组织(包括无织构组织)中, Db/Dm都大于2.5, 即组织中都存在大晶粒, 然而, 只有在σ=25~60的组织中, Db/Dm超过4并逐渐增大, 完全符合异常晶粒长大特征; 而在σ〈15和σ>60范围内, Db/Dm在2.5~4之间波动, 不完全符合异常晶粒长大特征, 本文中将之定义为各向异性条件下的正常晶粒长大。
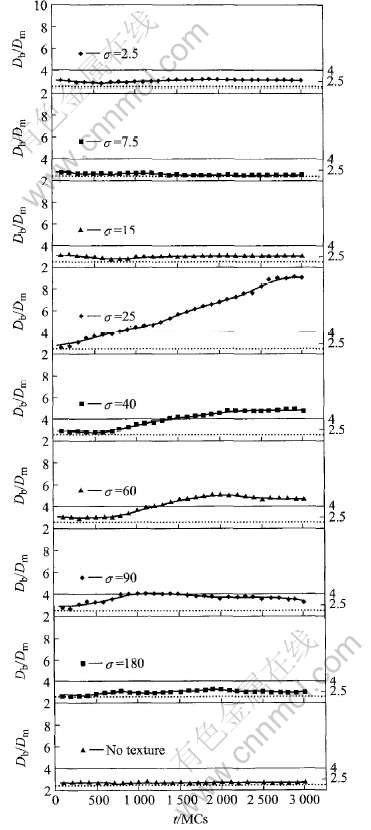
图6 织构强度对异常晶粒长大的影响
Fig.6 Effects of texture intensity on abnormal grain growing
总之, 异常晶粒长大出现在中等织构强度的组织中, 而不会在太强或太弱织构组织中出现。 太强或太弱织构组织中晶粒长大属于各向异性条件下的正常晶粒长大。
3.3 异常晶粒长大影响因素分析
为了从原理上说明晶界能和迁移率的各向异性对晶粒长大不均匀的影响, Rollett和Mullins设想了一个系统, 设一个单一晶粒A位于基体晶粒B中, 且边界AB与边界BB具有不同的能量和迁移率, 从而得到如下关系式[24]:
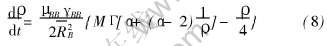
式中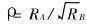 
, 表示晶粒A半径相对于基体B平均晶粒半径的比率; μBB为基体B内部晶界迁移率; γBB基体B内部晶界能; 
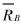B为基体中平均晶粒半径; Γ=γAB/γBB为晶界能的比率; M=μAB/μBB为晶界迁移率的比率; α为Γ的函数, α(Γ)=(6/π)×s sin-1(1/2Γ)。 当A晶粒晶界具有较小的晶界能和较大的迁移率(即Γ较小、 M较大)时, dρ/dt>0, 晶粒A比晶粒B更易于长大。
对于强织构组织, 晶粒取向大部分局限在一个小的角度范围, 组织中大都是小角度晶界, 晶界能和晶界迁移率的差别不大, 因此, 长大后的组织比较均匀, 不会出现异常晶粒长大; 对于弱织构及无织构组织, 组织中大都是大角度晶界, 晶界能和晶界迁移率的差别不大, 长大后的晶粒组织也相对均匀, 不会出现异常晶粒长大。 对于中等强度织构组织, 组织中大角度晶界和小角度晶界各占一定比例。 由于迁移率低, 具有小角度晶界的晶粒长大速度受阻, 而具有大角度晶界的晶粒有较大的长大速度, 容易快速长大。 因此, 组织中发生了异常晶粒长大。
从以上模拟和分析结果可知, 各向异性晶界能和晶界迁移率是异常晶粒长大的内因, 织构是引起异常晶粒长大的外因, 通过其强弱决定组织中的大角度晶界和小角度晶界的比例, 进而决定了异常晶粒长大是否出现。
4 结论
建立了一个新的MC Potts 模型, 在各向异性晶界能和晶界迁移率条件下, 模拟研究不同织构强度的初始组织晶粒长大特征, 得到以下结论:
1) 在各向异性晶界能和迁移率条件下, 组织特征偏离正常晶粒长大特征, 即组织中晶粒尺寸趋于非均匀、 形状趋于不规则; 晶粒长大速度慢于各向同性条件的晶粒长大速度, 晶粒长大指数小于各向同性下的晶粒长大指数, 远小于理论值0.5; 晶粒尺寸分布逐渐偏离对数正态分布; 晶粒尺寸分布范围变宽, 分布曲线不具备相似性。
2) 异常晶粒长大出现在中等织构强度的组织中, 而不会在太强或太弱织构组织中出现, 太强或太弱织构组织中晶粒长大属于各向异性条件下的正常晶粒长大。
3) 各向异性晶界能和晶界迁移率是异常晶粒长大的内因, 织构是引起异常晶粒长大的外因, 通过其强弱决定组织中大角度晶界和小角度晶界的比例, 进而决定了异常晶粒长大是否出现。
REFERENCES
[1]毛卫民, 赵新兵. 金属的再结晶和晶粒长大[M]. 北京: 冶金工业出版社, 1994. 218-219.
MAO Wei-ming, ZHAO Xin-bin. Metal recrystallization and grain growth[M]. Beijing: Metallurgical Industry Press, 1994. 218-219.
[2]Ma F, Zhang J M, Xu K W. Surface-energy-driven abnormal grain growth in Cu and Ag films[J]. Applied Surface Science, 2005, 242(1/2): 55-61.
[3]Straumal B B, Gust W, Dardinier L, et al. Abnormal grain growth in Al of different purity[J]. Materials and Design, 1997, 18(4/6): 293-295.
[4]Rios P R. Abnormal grain growth development from uniform grain size distributions in the presence of stable particles[J]. Scripta Materialia, 1998, 39(12): 1725-1730.
[5]Etter A L, Baudin T, Penelle R. Influence of the Goss grain environment during secondary recrystallisation of conventional grain oriented Fe-3%Si steels[J]. Scripta Materialia, 2002, 47(11): 725-730.
[6]Ivasishin O M, Shevchenko S V, Semiatin S L. Modeling of abnormal grain growth in textured materials[J]. Scripta Materialia, 2004, 50(9): 1241-1245.
[7]Ivasishin O M, Shevchenko S V, Vasiliev N L, et al. 3D Monte-Carlo simulation of texture-controlled grain growth[J]. Acta Materialia, 2003, 51(4): 1019-1034.
[8]Simpson C J, Aust K T, Winegard W C. Four stages of grain growth[J]. Met Trans, 1971, 2(4): 987-991.
[9]舒龙卫, 毛卫民, 冯惠平, 等. 冷轧低压电子铝箔退火加热过程中的再结晶和晶粒长大[J]. 中国有色金属学报, 2002, 12(1): 178-182.
SHU Long-wei, MAO Wei-ming, FENG Hui-ping, et al. Recrystallization and grain growth during annealing of cold rolled low voltage electronic aluminum foil[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(1): 178-182.
[10]Park J Y, Szpunar J A. Influence of the primary recrystallization texture on abnormal grain growth of goss grains in grain oriented electrical steels[J]. Materials Science Forum, 2002, 408-412(1): 821-826.
[11]Tomida T, Okamoto A, Takahashi M. Surface energy controlled abnormal grain growth in melt-quenched 6.6% silicon iron ribbons[J]. Tetsu-To-Hagane/Journal of the Iron and Steel Institute of Japan, 1988, 74(6): 1044-1051.
[12]Stout J J, Crimp M A, Abnormal grain growth in textured FeAl intermetallics[J]. Mater Sci Eng A, 1992, A152(1-2): 335-340.
[13]Srolovitz D J, Grest G S, Anderson M P. Computer simulation of recrystallization—Ⅰ: Homogeneous nucleation and growth[J]. Acta Metallurgica, 1986, 34(9): 1833-1845.
[14]Anderson M P, Srolovitz D J, Grest G S, et al. Computer simulation of grain growth—Ⅰ: Kinetics[J]. Acta Metallurgica, 1984, 32(5): 783-791.
[15]Srolovitz D J, Anderson M P, Grest G S, et al. Computer simulation of grain growth—Ⅲ: Influence of a particle dispersion[J]. Acta Metallurgica, 1984, 32(9): 1429-1438.
[16]Grest G S, Srolovitz D J, Anderson M P. Computer simulation of grain growth—Ⅳ: Anisotropic grain boundary energies[J]. Acta Metallurgica, 1985, 33(3): 509-520.
[17]Srolovitz D J, Grest G S, Anderson M P. Computer simulation of grain growth—Ⅴ: Abnormal grain growth[J]. Acta Metallurgica, 1985, 33(12): 2233-2247.
[18]Radhakrishnan B, Zacharia T. Simulation of curvature-driven grain growth by using a modified Monte Carlo algorithm[J]. Metall Mater Trans A, 1995, A26(1): 167-180.
[19]Rollett A D, Raabe D. A hybrid model for mesoscopic simulation of recrystallization[J]. Computational Materials Science, 2001, 21(1): 69-78.
[20]Wolf D. Read-Shockley model for high-angle grain boundaries[J]. Scripta Metallurgica, 1989, 23(10): 1713-1718.
[21]张继祥, 关小军, 孙胜. 一种改进的晶粒长大Monte Carlo模拟方法[J]. 金属学报, 2004, 40(5): 457-461.
ZHANG Ji-xiang, GUAN Xiao-jun, SUN Sheng. A modified monte carlo method in grain growth simulation[J]. Acta Metallurgica Sinica, 2004, 40(5): 457-461.
[22]张继祥, 关小军, 孙胜, 等. 晶粒长大过程微观组织演变Monte Carlo方法模拟[J]. 山东大学学报(工学版), 2004, 35(4): 1-5.
ZHANG Ji-xiang, GUAN Xiao-jun, SUN Sheng, et al. Monte Carlo simulation of microstructure evolution during grain growth[J]. Journal of Shandong University(Engineering Science), 2004, 35(4): 1-5.
[23]Humphreys F J. Unified theory of recovery, recrystallization and grain growth, based on the stability and growth of cellular microstructures—Ⅰ: The basic model[J]. Acta Materialia, 1997, 45(12): 4231-4240.
[24]Rollett A D, Mullins W W. On the growth of abnormal grains[J]. Scripta Materialia, 1997, 36(9): 975-980.
(编辑陈爱华)
基金项目: 山东省自然科学基金资助项目(Y2003F03)
收稿日期: 2006-04-01; 修订日期: 2006-07-05
通讯作者: 关小军, 教授; 电话: 0531-88396587; E-mail: xjguan@sdu.edu.cn
