Robust simultaneous tracking and stabilization of wheeled mobile robots not satisfying nonholonomic constraint
来源期刊:中南大学学报(英文版)2007年第4期
论文作者:祝晓才 董国华 蔡自兴 胡德文
文章页码:537 - 537
Key words:wheeled mobile robot; robust control; Lie group; transverse function; Lyapunov redesign
Abstract: A robust unified controller was proposed for wheeled mobile robots that do not satisfy the ideal rolling without slipping constraint. Practical trajectory tracking and posture stabilization were achieved in a unified framework. The design procedure was based on the transverse function method and Lyapunov redesign technique. The Lie group was also introduced in the design. The left-invariance property of the nominal model was firstly explored with respect to the standard group operation of the Lie group SE(2). Then, a bounded transverse function was constructed, by which a corresponding smooth embedded submanifold was defined. With the aid of the group operation, a smooth control law was designed, which fulfills practical tracking/stabilization of the nominal system. An additional component was finally constructed to robustify the nominal control law with respect to the slipping disturbance by using the Lyapunov redesign technique. The design procedure can be easily extended to the robot system suffered from general unknown but bounded disturbances. Simulations were provided to demonstrate the effectiveness of the robust unified controller.
基金信息:the National Natural Science Foundation of China
J. Cent. South Univ. Technol. (2007)04-0537-09
DOI: 10.1007/s11771-007-0104-2![]()
ZHU Xiao-cai(祝晓才)1, DONG Guo-hua(董国华)1, CAI Zi-xing(蔡自兴)2, HU De-wen(胡德文)1
(1. College of Mechatronic Engineering and Automation, National University of Defense Technology,Changsha 410073, China;
2. School of Information Science and Engineering, Central South University, Changsha 410083, China)
____________________________________________________________________________________________
Abstract:A robust unified controller was proposed for wheeled mobile robots that do not satisfy the ideal rolling without slipping constraint. Practical trajectory tracking and posture stabilization were achieved in a unified framework. The design procedure was based on the transverse function method and Lyapunov redesign technique. The Lie group was also introduced in the design. The left-invariance property of the nominal model was firstly explored with respect to the standard group operation of the Lie group SE(2). Then, a bounded transverse function was constructed, by which a corresponding smooth embedded submanifold was defined. With the aid of the group operation, a smooth control law was designed, which fulfills practical tracking/stabilization of the nominal system. An additional component was finally constructed to robustify the nominal control law with respect to the slipping disturbance by using the Lyapunov redesign technique. The design procedure can be easily extended to the robot system suffered from general unknown but bounded disturbances. Simulations were provided to demonstrate the effectiveness of the robust unified controller.
Key words: wheeled mobile robot; robust control; Lie group; transverse function; Lyapunov redesign
____________________________________________________________________________________________
1 Introduction
Lots of interest has been devoted to the control of wheeled mobile robots over the past decades. As pointed out by BROCKETT[1], nonholonomic systems, including wheeled mobile robots, cannot be asymptotically stabilized by any smooth time- invariant state feedback law. To overcome this technical obstacle, researchers have proposed three types of control laws, i.e., the smooth time-varying control laws, the discontinuous time-invariant control laws, and the hybrid control laws. Besides the stabilization problem, another basic control problem is trajectory tracking, which has also been heavily studied. For an in-depth overview of the control of nonholonomic systems, one can refer to Refs.[2-3].
In view of the existing references, it seems that, from a theoretic viewpoint, the problem of controlling wheeled mobile robots has been virtually solved. Nevertheless, there are still some issues deserving further attention. One of them is to design a unified controller that can simultaneously solve the tracking and stabilization problem. In general, the tracking and stabilization problems were studied separately. Therefore it is necessary to use two different controllers for the two tasks, and switching scheme between the two controllers is needed. Whereas in some practical occasions, e.g. the docking maneuver, such a switching is undesired, thus motivates the need of a unified controller for both stabilization and tracking. The research on unified controller design has received less attention. In Ref.[4], discontinuous controllers suitable for both stabilization and trajectory tracking were constructed based on dynamic feedback stabilization technique. The Lyapunov approach and backstepping technique were utilized in Ref.[5], in which the actuator saturation was also taken into account. DO et al[6] designed a unified controller using output-feedback approach, which is a more realistic way when the whole state of the system is not available.
Another issue, which has often been overlooked, is the control of wheeled mobile robots not satisfying ideal nonholonomic constraints. In most of the existing literatures, it is assumed that the wheels of the mobile robots are rolling on the ground without slipping. Although the ideal assumption is a reasonable approximation of the practical case when the robots move on hard ground at a low speed, it no longer works in some other real-world situations, especially when the ground is loose, and/or the speed of the wheeled mobile robots is fast. Compared with the abundant results of controlling wheeled mobile robots in ideal cases, fewer results have been reported when the slipping effect is considered. The pioneer research on stabilization in non-ideal cases was carried out in Ref.[7]. In Ref.[8], a singular perturbation approach was given for tracking control of wheeled mobile robots not exactly fulfilled velocity constraints. Time-varying tracking controller based on linear quadratic theory was proposed in Ref.[9]. MOTTE et al[10] used a slow manifold approach to design tracking control laws when there is slipping in the wheel/ground contact zones. DIXON et al[11-13] proposed robust tracking and stabilization controller for wheeled mobile robots with kinematic disturbances and parameters uncertainty using a brand-new dynamic oscillator approach.
From the aforementioned discussion, an open problem is to design a single controller that can solve both tracking and stabilization for wheeled mobile robots when the ideal nonholonomic constraint is destroyed. In this paper, a unified robust controller was proposed, which fulfills the practical tracking and stabilization of wheeled mobile robots when there are slips during the motion, through a systematic design process. The robust controller was designed based on the combination of the transverse function method[14-18] and the Lyapunov redesign technique[19]. The design procedure was facilitated with the aid of the nice structure of the Lie group SE(2). What’s more, no additional constraints were put on the reference trajectory; even the widely used “persistent excitation” assumption about the reference trajectory is no longer needed in the design process.
2 Problem formulation
2.1 Model of robot with slippingConsider a differential driven unicycle-type wheeled mobile robot not satisfying the ideal rolling without slipping assumption. Its kinematic model is given as follows[7]:
![]() (1)
(1)
where ![]() , q=(x, y, θ)T,
, q=(x, y, θ)T, ![]() is the coordinate of the center of the mass of the wheeled mobile robot; θ is the orientation with respect to the x-axis of the inertial reference frame. The input matrix B(q) is defined as follows:
is the coordinate of the center of the mass of the wheeled mobile robot; θ is the orientation with respect to the x-axis of the inertial reference frame. The input matrix B(q) is defined as follows:
 (2)
(2)
and the kinematic input u is
u=(v ω)T (3)
where v is the translational velocity of the center of mass, ![]() is the angular velocity around the vertical axis of the body frame. The corresponding nominal system is
is the angular velocity around the vertical axis of the body frame. The corresponding nominal system is
![]() (4)
(4)
which is controllable in nonlinear context[20], whereas it does not meet the Brockett’s necessary condition.
Denote the slipping effect by a unknown but bounded time-varying function ρ(t) with known positive bound ζ, i.e., ![]() ≤ξ. When the ideal nonholonomic constraints are satisfied, the equation
≤ξ. When the ideal nonholonomic constraints are satisfied, the equation ![]() =0 holds. If the ideal constraint is violated, the “scale” of the slipping can be expressed as
=0 holds. If the ideal constraint is violated, the “scale” of the slipping can be expressed as
![]() (5)
(5)
Note that ρ(t) is independent of the system states in general, thus Eqn.(5) is only a result of the slipping phenomenon, not the cause. Obviously, the corresponding disturbance introduced by the slipping is unmatched disturbance, and plays the role of nonvanishing perturbation.
The reference trajectory qr(t) is assumed to be generated by a reference system given as
![]() (6)
(6)
qr=(xr, yr, θr)T is the reference state, ur is the reference inputs. Throughout this paper, it is assumed that ur is piecewise continuous and bounded function. Note that the dimension of ur is not necessarily equal to that of u, hence the reference trajectory may not be a solution of the nominal system.
2.2 Existence of unified controllerFrom Section 1 we know that for nonholonomic systems, asymptotic stabilization cannot be achieved by any smooth static state feedback. That is, the system’s states cannot be asymptotically stabilized to any equilibrium point, i.e. constant trajectory that is not persistently exciting (PE). Nevertheless, the system’s state can be asymptotically stabilized to any PE reference trajectory. The persistent excitation condition that has become a standard assumption when asymptotic trajectory tracking problem is considered, rules out constant reference trajectory. For example, let Br(qr)=B(qr), ur=(vr, ωr)T, and the input error variables as ![]() ,
, ![]() . Define the state tracking error as
. Define the state tracking error as
 (7)
(7)
then the tracking error system is
 (8)
(8)
It’s easy to check that the controllability Gramian of the above system is nonsingular if and only if either ![]() or
or ![]() are nonzero. Thus it seems that there is no unified controller. Actually, as proven in Ref.[21], there does not exist any piecewise continuous feedback that can solve both tracking and stabilization problems in the sense of “asymptotic”, even time-varying feedback is used. In turn, relaxing the convergence requirement is theoretically justified in unified controller design process.
are nonzero. Thus it seems that there is no unified controller. Actually, as proven in Ref.[21], there does not exist any piecewise continuous feedback that can solve both tracking and stabilization problems in the sense of “asymptotic”, even time-varying feedback is used. In turn, relaxing the convergence requirement is theoretically justified in unified controller design process.
On one hand, it is obvious that the linearization of the nominal system (4) has an uncontrollable eigenvalue at the origin. From the classic linear system theory[22], it is known that the nominal system cannot be exponentially stabilized by any smooth control law. Moreover, it does not meet the Brockett’s necessary condition, thus it is not asymptotically stabilizable by any smooth static control law. These make the asymptotic stabilization problem of wheeled mobile robots nontrivial. As pointed out in Ref.[16], the classical asymptotic stabilization is too restrictive and too constraining to some extent, thus settling for practical stabilization other than asymptotic stabilization may be a more realistic control object to pursue.
On the other hand, if the slipping function ρ(t) is not identically zero, then the corresponding disturbance acts as a nonvanishing perturbation to the nominal system. In this case, the origin may not be an equilibrium point of the nominal system. So, it is no sense to study the stability of the origin as an equilibrium point, nor should one expect the solution of the nominal system to approach the origin as t→∞. The best hope is that if the perturbation is small in some sense, then the system states will be ultimately bounded by a small bound[19]. As for the trajectory tracking case, because the tracking problem is usually treated as an equivalent stabilization problem of the corresponding tracking error system, when there is nonvanishing perturbation, the best we can hope for is the tracking error variables being ultimately bounded.
Thus, in real-world applications, the following practical stabilization/tracking problem may be more realistic and easily attained. That’s one of the motivations that this paper pursues unified stabilization and tracking in the sense of “practical”.
2.3.1 Practical tracking control problem
Find robust control laws for ν and ω, such that the wheeled mobile robot with the perturbed kinematic model (1) follows a reference trajectory qr(t) generated by the reference system (6) up to a given tracking error bound δ>0. That is, for some suitably defined error variable ![]() , there is a positive constant T0 such that
, there is a positive constant T0 such that
![]() (9)
(9)
2.3.2 Practical stabilization control problem
Find robust control laws for ν and ω, such that the wheeled mobile robot with the perturbed kinematic model (1) is driven to a vicinity of the origin up to a given error bound δ>0. That is, for the system states q(t), there exists a positive constant T0 such that
![]() (10)
(10)
Note that it is not explicitly described here what kind of error variable definition is suitable. In what follows, it will take advantage of a particular invariance property of the nominal system in the definition. Furthermore, one will see that when ur=0, the practical tracking control problem is reduced to the practical stabilization case. With the aid of transverse function, the unified tracking and stabilization control can be solved in the sense of “practical”, despite the reference trajectory is PE or not.
3 Controller synthesis
3.1 Left-invariance of nominal systemThe nominal system (4) can be viewed as a system on the Lie group SE(2), i.e., R2×S1. The natural group operation ![]() is defined by
is defined by
 (11)
(11)
where the matrix R(θ1) represents the rotation of angle θ1 in R2. Obviously, under the group operation, the unit element of the Lie group is e=(0, 0, 0)T, and the right-inverse of q is defined as the unique element q-1∈SE(2) satisfying![]() .
.
One of the reasons for the concept of Lie group is introduced in the design procedure is that, as a system on Lie group, the nominal system has a special intrinsic geometric structure, which endows the system with a particular invariance property with respect to the group operation[23]. The left-invariance property of the system is stated as follows.
Proposition 1: The nominal system (4) is left- invariant with respect to the group operation (11).
The proof is trivial, thus it is leaved out here.
3.2 Transverse function and dynamic augmentationThe existence of bounded transverse function is vital for the design, which is ensured by the controllability of the nominal system [16].
Proposition 2[14]: For![]() , the mapping f? S-1→SE(2) defined as follows is a transverse function:
, the mapping f? S-1→SE(2) defined as follows is a transverse function:
 (12)
(12)
Define the “transversality matrix” H(θ) as
![]() (13)
(13)
where Xi(i=1,…,m) are the vector fields of a corresponding system, then the coordinate-dependent version of the transversality condition is
![]() (14)
(14)
The transverse function defines a submanifold of the state space. The submanifold M=f(S1) is essentially a smooth embedding of 1-torus (or the circle) S1=R/(2πZ) into the Lie group SE(2), and its size is determined by a positive parameter ε, which can be arbitrarily predetermined. A sufficiently small ε will make the submanifold M close enough to the origin. Augment the nominal system by an element α∈T that is directly controlled by an additional input ζ as
 (15)
(15)
In the subsequent control design, the additional state ![]() and the additional input ζ act as “freedoms” of control. This is the main difference between the transverse function method and the classic time-varying algorithm.
and the additional input ζ act as “freedoms” of control. This is the main difference between the transverse function method and the classic time-varying algorithm.
How to suitably define error variables is important because “good” definition will bring convenience to the control design. There are two error variables to be defined in the design framework, one is denoted by ![]() that is the trajectory tracking error of the robot between the actual states and the reference states; the other is denoted by z that is the error between the just obtained
that is the trajectory tracking error of the robot between the actual states and the reference states; the other is denoted by z that is the error between the just obtained ![]() and the embedded submanifold M. Noticing that the nominal system is left-invariant with respect to the group operation of SE(2), one can take advantage of this property in the sequel. Hence, instead of defining the tracking error vector in a “traditional” way such as
and the embedded submanifold M. Noticing that the nominal system is left-invariant with respect to the group operation of SE(2), one can take advantage of this property in the sequel. Hence, instead of defining the tracking error vector in a “traditional” way such as![]()
![]() , it is done in the manner of group operation as
, it is done in the manner of group operation as
![]() (16)
(16)
and the other error vector z as
![]() (17)
(17)
Differentiating the above equation we get
![]() (18)
(18)
Because![]() , and
, and
![]() (19)
(19)
the time derivative of ![]() is
is
![]()
 (20)
(20)
With the aid of the left-invariance property of the nominal system, Eqn.(18) can be rewritten as

 (21)
(21)
further calculation shows that
![]()
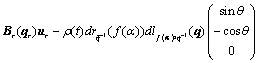 (22)
(22)
i.e.
![]()
![]() (23)
(23)
where the matrix H(α) is exactly the nonsingular “transverse matrix” given in Eqn.(13). Then, after the augmentation in the previous subsection, the z-system now becomes full-actuated, no longer underactuated as in Eqn.(1).
3.4 Robust controller designFirstly, assuming that there is no slipping in the motion, design nominal stabilizing control laws for the nominal error system, i.e.![]() (24)
(24)
Obviously, the matrix ![]() is nonsingular, and its inverse is given by
is nonsingular, and its inverse is given by
![]() (25)
(25)
Define
![]() (26)
(26)
if the control laws are constructed as
 (27)
(27)
where K is any positive-definite matrix. The resulted
closed-loop system is
![]() (28)
(28)
A candidate Lyapunov function for the above resulted linear system is V1=zTz/2, under the control laws (27), the derivative ![]() is negative- definite. Therefore the nominal error system (24) is exponentially stabilized.
is negative- definite. Therefore the nominal error system (24) is exponentially stabilized.
Obviously, in nominal control laws (27), the information of the reference trajectory is included in the term τ. The matrices H-1(α) and ![]() are not singular, no matter the reference trajectory qr(t) is PE or not. It is this property that gets rid of the PE constraint, thus allows the stabilization and tracking problems be solved in an unified framework.
are not singular, no matter the reference trajectory qr(t) is PE or not. It is this property that gets rid of the PE constraint, thus allows the stabilization and tracking problems be solved in an unified framework.
Now, construct the robust tracking control laws based on the control laws (27). Define
![]() (29)
(29)
then the error system (18) is rewritten as
![]() (30)
(30)
Define λ=(λ1, λ2, λ3)T, add an additional term to the nominal control laws as
 (31)
(31)
Then, the derivative of the candidate Lyapunov function ![]() is given as
is given as
![]()
![]() (32)
(32)
Choose
![]() (33)
(33)
then
![]()
![]() (34)
(34)
Hence, under robust control laws (31)-(33), the error system (23) is asymptotically stable, and the error vector z→0. Consequently, we know that ![]() , i.e. the tracking error converges to the embedded submanifold M. Because the distance between the submanifold M and the origin is predetermined by the positive parameter ε, and f(α)→0 when ε→0, thus from the definition of
, i.e. the tracking error converges to the embedded submanifold M. Because the distance between the submanifold M and the origin is predetermined by the positive parameter ε, and f(α)→0 when ε→0, thus from the definition of ![]() it is known that q(t)→qr(t) when t→∞, ε→0, i.e. the actual trajectory q(t) of the robot system (1) is confined in a “belt” about the reference trajectory qr(t). Therefore, the proposed robust tracking controller achieves “practical” trajectory tracking subjected to slipping effect. To increase the control precision one can decrease the parameter ε of the transverse function. However, smaller
it is known that q(t)→qr(t) when t→∞, ε→0, i.e. the actual trajectory q(t) of the robot system (1) is confined in a “belt” about the reference trajectory qr(t). Therefore, the proposed robust tracking controller achieves “practical” trajectory tracking subjected to slipping effect. To increase the control precision one can decrease the parameter ε of the transverse function. However, smaller ![]() results in stronger oscillation, thus greater control effort is needed because the parameter
results in stronger oscillation, thus greater control effort is needed because the parameter ![]() also appears in the denominator of the control law.
also appears in the denominator of the control law.
Remark 1: From Eqn.(28) one can see that the nominal error system (24) is linearized by the control laws (27), and will be decoupled if the matrix K is a diagonal matrix. Such kind of linearization is called “practical linearization”. The common points which it shares with the dynamic feedback linearization are that the linearization results are both exact, and they all experience a dynamic augmentation procedure. The difference is that for wheeled mobile robots, there is a potential singularity in dynamic feedback linearization algorithm, and it is an intrinsic obstacle of the nonholonomic system, whereas there is no singularity in the practical linearization algorithm.
3.5 Posture stabilizationThere are qr(t)≡0 and ur(t)≡0 in the stabilization case. The purpose of the practical stabilization is to render the system’s state near the origin, i.e. the constant reference trajectory qr(t)≡0 in view of the tracking control framework. Similar to the error definition in tracking case, define the state error variable in group operation manner as
![]() (35)
(35)
Recall e=(0, 0, 0)T, thus qr(t)≡e. Therefore, the origin is actually the unit element of the Lie group SE(2). Because
![]() (36)
(36)
then Eqn.(35) becomes
![]() (37)
(37)
which is the same as Eqn.(17). Note that in the tracking case the standard PE condition is no longer needed, then the stabilization problem is naturally covered by the trajectory tracking problem, and then the control laws (31)-(33) are able to solve both the stabilization and trajectory tracking problems. In the stabilization problem, under the unified controller, the state of system (1) converges to the embedded submanifold M, i.e. q→f(α). Thus the system’s state q can be rendered arbitrarily close to the origin, and the practical stabilization is achieved.
4 Extending to general disturbance
It is trivial to extend the above procedure to the unified control of wheeled mobile robots subjected to general bounded disturbances. Consider a unicycle robot suffered from unknown disturbance, the kinematic model of the robot is given as
![]() (38)
(38)
with ρi(t)(i=1,2,3) is some unknown but bounded functions. Assume that the known bounds are
![]() ≤ξi, i=1, 2, 3 (39)
≤ξi, i=1, 2, 3 (39)
where ξi are positive. Such kind of disturbance covers both matched/unmatched disturbances and vanishing/nonvanishing perturbations. Following the same routine of the tracking case, one can get the error system as:
![]()
 (40)
(40)
Define
![]() (41)
(41)
and choose
![]() (42)
(42)
then, under the control law (31)-(42) the derivative of the candidate Lyapunov function is
 ≤-zTKz-
≤-zTKz-![]() ≤-zTKz (43)
≤-zTKz (43)
Through the similar analysis it can be shown that the practical tracking/stabilization is achieved.
5 Simulations and discussion
5.1 Trajectory tracking
In the simulations of trajectory tracking, the slipping effect was given as
ρ(t)=0.1[H(t-8)-H(t-12)] (44)
where H(?) is the standard Heaviside step function. The expression means that when t∈[8, 12], slipping occurs in the motion of the wheeled mobile robot, and the amplitude of the slipping is 0.1. The matrix K was set to diag(1, 1, 1), and ![]() was assigned to be
was assigned to be ![]() . The initial state was (4, 3, π/6, 0). Let Br(qr)=B(qr), and set νr=1, ωr=0.2. The simulation lasted for 25 s, hence the reference trajectory was an arc which was approximately
. The initial state was (4, 3, π/6, 0). Let Br(qr)=B(qr), and set νr=1, ωr=0.2. The simulation lasted for 25 s, hence the reference trajectory was an arc which was approximately ![]() of a circle.
of a circle.
Fig.1 shows the practical tracking of the arc trajectory. The dotted arc is the reference trajectory, and the solid line is the actual trajectory of the mobile robot. The tracking errors defined as the traditional way (q-qr) are depicted in Fig.2. The two figures show that although there is slipping in the motion, the reference trajectory is still successfully tracked by the mobile robot, thus the theoretic analysis is verified. Fig.3 shows the evolution of the augmented kinematic control inputs (ν, ω, ζ) that remain bounded. From Fig.4 one can see that the error variables zi, (i=1, 2, 3) converge to zero, as a result, the state of the robot system is stabilized to the embedded submanifold M. Fig.5 illustrates the evolution of the additional state α. The value the additional state α converges to is not concerned, whereas what we concern is whether it converges and whether the corresponding additional input ζ remains bounded. It is obvious that α does converge from Fig.5, and ζ does remain bounded from Fig.3.

Fig.1 Actual and reference trajectories of mobile robot

Fig.2 Traditional tracking error
(a) x-xr; (b) y-yr; (c) θ-θr

Fig.3 Time plots of augmented control input (ν, ω, ζ)
(a) ν; (b) ω; (c) ζ

Fig.4 Evolutions of error vector z: (a) z1; (b) z2; (c) z3

Fig.5 Evolution of additional state α
5.2 Posture stabilizationIn the stabilization simulations, the slipping effect was given as
ρ(t)=-0.1[H(t-2)-H(t-6)] (45)
thus when t∈[2, 6] there exists slipping with amplitude 0.1. The initial state is(10, 8, π/3, 0).
Figs.6 and 7 show the evolution of the augmented system state(x, y, θ, α). It can be seen that all of the states converge to some value respectively, and they all remain bounded. From Fig.6 one can see that at first, the convergent speed is high: the robot is almost stabilized to the origin at t=2 s, then the slipping happens. In what follows, oscillations appear in the robot’s motion. After t=18 s, the effect of the slipping is dominated by the robust control laws, thus the oscillations disappear. The boundedness of the augmented kinematic control input is depicted in Fig.8. It is obvious from Fig. 9 that the error variable z converge to zero, then the states of the robot system are stabilized to the submanifold M. Fig.10 illustrates the Cartesian trajectory of the robot subjected to slipping effect. The oscillation in the trajectory near the origin is mainly caused by the slipping effect, as shown in Fig.6. The mobile robot is eventually stabilized to the vicinity of the origin, thus coincides with the theoretic analysis.
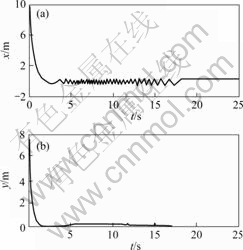
Fig.6 Time plot of states x(a) and y(b)
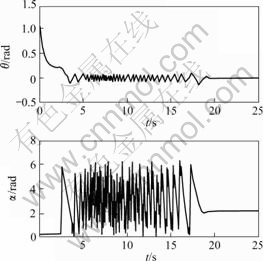
Fig.7 Time plot of states θ and α

Fig.8 Evolution of augmented control input
(a) ν; (b) ω; (c) ζ

Fig.9 Evolution of error vector z=(z1, z2, z3)

Fig.10 Cartesian trajectory of mobile robot
6 Conclusions
1) Robust control laws were proposed for the unified practical tracking and stabilization control problem of wheeled mobile robots not satisfying ideal nonholonomic constraints.
2) The transverse function method is a systematic control design method, and its ability of fulfilling the linearization of the corresponding error system makes it easily cooperated with some Lyapunov-based techniques such as integrator backstepping and Lyapunov redesign.
3) There are no additional constraints put on the reference trajectory, and the widely used “persistent excitation” assumption on the reference trajectory is not required in the design process, thus allowing the simultaneously tracking and stabilization control problem to be solved in an elegant way. Moreover, the reference trajectory is neither assumed to satisfy the nonholonomic constraints, nor to be a solution of the original system equation. Therefore, the robot is endowed with the ability to practically tracking any reference trajectory.
References
[1] BROCKETT R W. Asymptotic stability and feedback stabilization[C]// BROCKETT R W, MILLMAN R S, SUSSMANN H J. Differential Geometric Control Theory. Boston: Birkhauser, 1983: 181-191.
[2] KOLMANOVSKY I, MCCLAMROCH N H. Developments in nonholonomic control systems[J]. IEEE Control System Mag, 1995, 15(6): 20-36.
[3] LUCA A D, ORIOLO G, VENDITTELLI M. Control of wheeled mobile robots: An experimental overview[C]// NICOSIA S, SICILIANO B, BICCHI A, et al. RAMSETE—Articulated and Mobile Robotics for Services and Technologies. Berlin: Springer, 2001: 181-226.
[5] LEE T C, SONG K T, LEE C H, et al. Tracking control of unicycle-modeled mobile robots using a saturation feedback controller[J]. IEEE Transactions on Control Systems Technology, 2001, 9(2): 305-318.
[7] de CANUDAS WIT C, KHENNOUF H. Quasi-continuous stabilizing controllers for nonholonomic systems: Design and robustness considerations[C]// Proc 3rd Euro Contr Conf Rome, Italy: IEEE Press, 1995: 2630-2635.
[8] D’ANDREA-NOVEL B, CAMPION G, BASTIN G. Control of wheeled mobile robots not satisfying ideal velocity constraints: A singular perturbation approach[J]. International Journal of Robust and Nonlinear Control, 1995, 5(2): 243-267.
[9] LEROQUAIS W, D’ANDREA-NOVEL B. Modeling and control of wheeled mobile robots not satisfying ideal velocity constraints: the unicycle case[C]// Proc 35th Conf Decision Control. Kobe, Japan: IEEE Press, 1996: 1437-1442.
[10] MOTTE I, CAMPION G. A slow manifold approach for the control of mobile robots not satisfying the kinematic constraints[J]. IEEE Transactions on Robotics and Automation, 2000, 16(6): 875-880.
[11] DIXON W, DAWSON D, ZHANG F, et al. Global exponential tracking control of mobile robot system via a PE condition[J]. IEEE Trans Syst Man Cybern B, 2000, 30(1): 129-142.
[12] DIXON W E, DOWSON D M, ZERGEROGLU E, et al. Robust tracking and regulation control for mobile robots[J]. International Journal of Robust and Nonlinear Control, 2000, 10(2): 199-216.
[13] DIXON W E, de QUEIRROZ M S, DOWSON D M, et al. Adaptive tracking and regulation of a wheeled mobile robot with controller/update law modularity[J]. IEEE Transactions on Control Systems Technology, 2004, 12(1): 138-147.
[14] MORIN P, SAMSON C. Practical stabilization of a class of nonlinear systems: Application to chain systems and mobile robots[C]// Proc 39th IEEE Conf Decision Contr. Sydney, Australia: IEEE Press, 2000: 2989-2994.
[15] MORIN P, POMET J B, SAMSON C. Design of homogeneous time-varying stabilizing control laws for driftless controllable systems via oscillatory approximation of Lie brackets in closed loop[J]. SIAM Journal on Control and Optimization, 2000, 38(1): 22-49.
[16] MORIN P, SAMSON C. Practical stabilization of driftless systems on Lie groups: The transverse function approach[J]. IEEE Transactions on Automatic Control, 2003, 48(9): 1496-1508.
[17] MORIN P, SAMSON C. A characterization of the Lie algebra rank condition by transverse periodic functions[J]. SIAM Journal on Control and Optimization, 2002, 40(4): 1227-1249.
[18] MORIN P, SAMSON C. Practical and asymptotic stabilization of chained systems by the transverse function control approach[J]. SIAM Journal on Control and Optimization, 2004, 43(1): 32-57.
[19] KHALIL H K. Nonlinear Systems[M]. 2nd ed. Upper Saddle River: Prentice-Hall, 1996.
[20] ISIDORI A. Nonlinear Control Systems[M]. 3rd ed. Berlin: Springer-Verlag, 1995.
[21] LIZARRAGA D A. Obstructions to the existence of universal stabilizers for smooth control systems[J]. Mathematics of Control, Signals, and Systems, 2003, 16: 255-277.
[22] ZHENG Da-zhong. Linear System Theory[M]. 2nd ed. Beijing: Tsinghua University Press, 2002. (in Chinese)
[23] SPIVAK M. A Comprehensive Introduction to Differential Geometry[M]. 2nd ed. vol. I. Houston: Perish Inc, 1979.
__________________________
Foundation item: Project (60234030) supported by the National Natural Science Foundation of China; Project supported by the TRAPOYT of Ministry of Education of China
Received date: 2007-01-11; Accepted date: 2007-03-27
Corresponding author: ZHU Xiao-cai, PhD; Tel: +86-731-4574977; E-mail: zhuxiaocai@163.com

