DOI: 10.11817/j.issn.1672-7207.2016.09.015
直驱式主动前轮转向电液位移系统双滑模控制
黄开启1, 2,陈荣华2,迟永滨1
(1. 华南理工大学 机械与汽车学院,广东 广州,510640;
2. 江西理工大学 机电工程学院,江西 赣州,341000)
摘要:针对直驱容积式主动前轮转向位移伺服系统存在参数时变、外界干扰以及滑模抖振问题,设计一种汽车液压助力主动转向集成系统,结合神经网络和自适应控制算法,提出一种活塞杆位移与电机转速双滑模控制策略。活塞杆位移采用等效加切换控制律,选用积分形式的快速收敛滑模面设计电机速度等效控制律,利用神经网络对控制律的变化在线估测,并结合自适应算法进行补偿,以抑制传统滑模控制律幅值过大的正负高频切换信号导致的系统抖振,根据Lyapunov理论分析系统的稳定性。研究结果表明:与传统的滑模控制相比,所提出的控制策略不仅能实现对期望位移的准确跟踪,而且能有效削弱系统抖振,增强系统的鲁棒性。
关键词:主动前轮转向;永磁同步电机;容积控制;神经网络;自适应;双滑模控制
中图分类号:TP273 文献标志码:A 文章编号:1672-7207(2016)09-3011-09
Double sliding mode control for direct-drive hydraulic servo active front steering system
HUANG Kaiqi1, 2, CHEN Ronghua2, CHI Yongbin1
(1. School of Mechanical and Automotive Engineering, South China University of Technology,
Guangzhou 510640, China;
2. School of Mechanical and Electrical Engineering, Jiangxi University of Science and Technology,
Ganzhou 341000, China)
Abstract: A type of hydraulic power and active steering system for vehicle was designed for dealing with the parameter uncertainties, external disturbance and sliding mode chattering exited in the direct-driven active front steering hydraulic servo system. And a control strategy of piston-rod displacement and motor-speed double sliding-mode control was proposed combined with neural network and self-adaptation control algorithm. The equivalent control and switch control were designed for the piston-rod displacement control law, and the motor speed equivalent control law was designed based on the fast convergence sliding surface of integral form. In order to restrain the system chattering caused by the traditional sliding-mode controller with plus-minus high frequency switching signal of excessive amplitude, the neural network online estimation for the control law change and self-adaptation control algorithm was adopted. Furtherly, Lyapunov theory was used to prove its stability. The results show that the control strategies can not only track the expected displacement accurately, but also weaken the chattering and enhance the robustness of system effectively.
Key words: active front steering; permanent magnet synchronous motor; volume control; neural network; self-adaptation control; double sliding mode control
力矩与角位移传递特性是转向系统重要的性能指标,直接关系到汽车的舒适性、操纵稳定性和行车安全。助力转向(power steering,PS)控制力矩传递特性,通过助力、回正和阻尼控制,满足汽车转向轻便性和“路感”要求[1-2]。主动前轮转向(active front steering,AFS) 控制角位移的传递特性,通过变传动比和直接转向干预,优化轮胎力及其力矩分布,补偿轮胎侧偏刚度摄动和抵抗外界干扰,提高了横摆角速度增益水平,改善了汽车转向灵敏性、操纵稳定性和主动安全性,是一种重要的汽车主动安全技术[3-4]。电动双行星齿轮AFS结构复杂,体积大,机构产生的反作用力影响了转向手感[5-6]。线控转向(steer-by-wire,SBW)取消了方向盘与转向前轮之间的机械连接,其可靠性仍待提高[7-8]。力矩与角位移分工与协同控制研究是提高汽车舒适性、操纵稳定性和主动安全的关键技术。目前,PS与AFS多为独立的2个子系统,结构复杂,安装成本高,难以实现力矩与角位移的协同控制[9-10]。电动液压助力转向系统具有出力大、吸振、可靠性高和“路感”清晰等独特优点,是中、高级乘用车和各种大型车辆转向系统的最佳实现方案[11-12]。为提升转向系统性能指标,充分发挥其对汽车操纵稳定性的作用,在电动液压助力转向系统的基础上,将PS与AFS集成于双伸缩缸转向器,结合永磁同步电机(permanent magnet synchronous motor,PMSM)动态特性好和控制精度高等优点及齿轮泵结构简单、抗污染能力强等特点,设计了一种新型电动液压直驱容积式主动转向伺服系统[13-14]。直驱容积式位移伺服系统参数随工况变化而变化,同时还存在负载扰动、非线性摩擦及子系统之间的力与位移耦合等问题[15-17],为此,本文作者提出一种活塞杆位移与电机速度双闭环滑模控制策略,以增强系统的鲁棒性。由于实际执行机构存在时间上延迟和空间上滞后,而传统滑模控制器幅值较大的高频正负切换输出使滑动模态难以准确发生在设定的理想切换流形面上,容易引起系统抖振[18]。利用神经网络万能逼近能力在线估测控制律的变化,并结合自适应控制算法对变化律进行补偿,以削弱传统滑模固有的抖振,提高系统的综合品质。
1 新型转向系统设计与工作模式
1.1 新型转向系统设计
新型电动液压转向集成系统如图1所示,包括双伸缩缸转向器、电机齿轮泵、传感器、车辆ECU (electronics control unit)、电机控制器、转阀、换向阀及液压辅助元件等。
一级油缸用于主动转向,压油经活塞杆1(转向横拉杆)的空心油路进入油缸,推动活塞杆1进行主动前轮转向。二级油缸用于助力转向,缸筒5的外圆中间段制有齿条2并与转向小齿轮4啮合,缸筒5装于壳体6的内两侧并活套在活塞杆1上,缸筒5与壳体6之间为助力油腔,方向盘转动驱动齿条2和缸筒5移动,同时打开转阀使压油进入助力油腔,实现助力转向。
工作时,车辆ECU需检测车速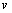 、方向盘转角
、方向盘转角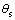 和转矩Te。电机控制器检测活塞杆1的位移xp并输出电机泵转速
和转矩Te。电机控制器检测活塞杆1的位移xp并输出电机泵转速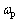 和电磁阀开关信号sv。
和电磁阀开关信号sv。
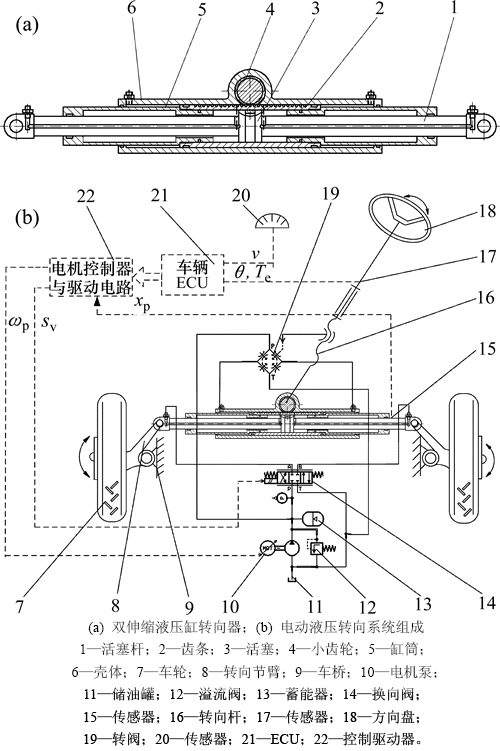
图1 新型电动液压转向集成系统
Fig. 1 New intergrated electro-hydraulic steering system
1.2 工作模式
该系统有以下3种工作模式。
1) 助力转向模式。助力转向单独工作时,换向阀14闭合,AFS油缸成为一刚性连杆。此模式与普通电动液压助力转向系统相同。
2) 主动前轮转向模式。方向盘无转向输入,转阀19闭合,缸筒5和活塞杆1无相对位移,形成一刚性杆件。通过控制电机转速和换向阀动作,压油经活塞杆1空心油路进入主动转向油缸,推动活塞杆1移动,并驱动转向节臂8进行主动转向。此模式用于汽车受外界扰动、危险工况或驾驶员转向操作不到位的情况,通过直接转向干预对汽车进行操纵稳定性主动控制。
3) 变传动比模式。方向盘转向时,活塞杆1一侧进油,推动活塞杆1相对于缸筒5轴向移动,此时,活塞杆1的位移为齿条驱动缸筒5的位移和活塞杆1相对于缸筒5的位移的叠加,实现变传动比控制,提高汽车的转向灵敏性和操纵稳定性。
双伸缩缸高度集成PS和AFS,具有结构紧凑、液压元件少、安装成本低、可靠性高等优点,能方便实现对力矩与角位移的分工与协同控制,有效改善了转向系统的综合性能。
2 控制系统设计
2.1 控制系统方案
AFS电液位移控制系统采用双闭环控制,即活塞杆位移外环控制和电机转速内环控制,其中,电流采用PI控制,系统结构如图2所示。
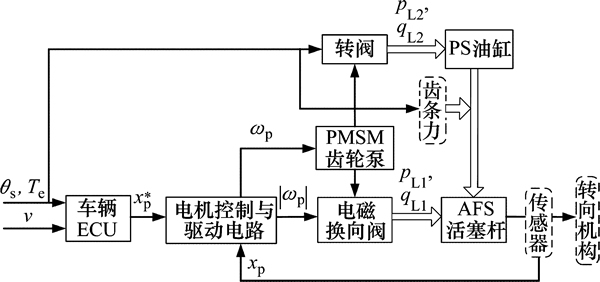
图2 控制系统总体方框图
Fig. 2 General block diagram of control system
系统采用分层结构设计,顶层车辆ECU实时检测方向盘输入和车速等工况参数,根据汽车操纵稳定性控制算法决策出前轮转角,换算成横拉杆位移后并送至底层控制器,利用本文设计的控制算法,底层控制器通过控制电机转速并驱动换向阀动作,为系统提供压油,实现对横拉杆位移的准确跟踪。
2.2 控制系统建模
液压缸流量平衡方程为
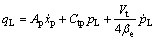 (1)
(1)
液压缸负载力平衡方程为
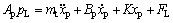 (2)
(2)
式中:Ap为液压缸活塞有效面积;qL为负载流量,pL为负载压降,即图2中的qL1和pL1,为了区别,PS系统的负载流量和负载压降为qL2和pL2;Ctp为液压缸总泄漏系数;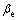 为油液体积模量;Vt为液压缸总压缩容积;xp为活塞杆位移;mt为活塞杆的等效质量;Bp为黏性系数;K为弹性刚度系数;FL为作用在活塞上的外负载力。
为油液体积模量;Vt为液压缸总压缩容积;xp为活塞杆位移;mt为活塞杆的等效质量;Bp为黏性系数;K为弹性刚度系数;FL为作用在活塞上的外负载力。
汽车在原地转向时,负载力为车轮与地面间的摩擦阻力;在行驶过程中,车轮转角小于3°~5°,当侧向加速度不超过0.4g时,负载力主要为轮胎侧偏形成的回正力矩,负载刚度等效成轮胎侧偏刚度[19]。
电机齿轮泵流量qp为
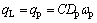 (3)
(3)
式中:Dp为齿轮泵排量;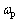 为电机泵的转速;C为容积效率。
为电机泵的转速;C为容积效率。
将式(3) 2边同除以Dp,得
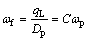 (4)
(4)
式中: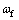 为广义转速[14]。电机泵的负载转矩TL为
为广义转速[14]。电机泵的负载转矩TL为
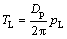 (5)
(5)
考虑系统参数时变、非线摩擦和外界干扰,结合式(1)、式(2)和式(4),AFS活塞杆位移模型为
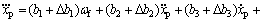
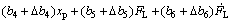 (6)
(6)
式中: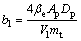 ;
;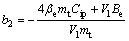 ;
;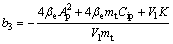 ;
;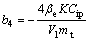 ;
;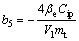 ;
;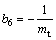 ;△b1,△b2,△b3,△b4,△b5和△b6为参数变化部分;
;△b1,△b2,△b3,△b4,△b5和△b6为参数变化部分;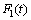 为液压系统总的不确定部分,
为液压系统总的不确定部分,
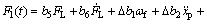
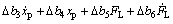 (7)
(7)
则液压伺服系统动力学方程为
 (8)
(8)
式中: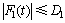 ,D1为干扰界。
,D1为干扰界。
永磁同步电机旋转坐标系的数学模型[20]为
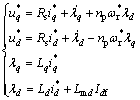 (9)
(9)
式中: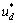 和
和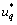 分别为d和q坐标下的定子电压;
分别为d和q坐标下的定子电压;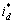 和
和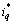 分别为d和q坐标下的定子电流;
分别为d和q坐标下的定子电流;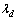 和
和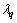 分别为d和q坐标下的定子磁链;
分别为d和q坐标下的定子磁链;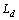 和
和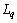 分别为d和q坐标下的电感分量;
分别为d和q坐标下的电感分量;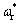 为电机给定转速;
为电机给定转速;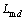 为定子相电感;
为定子相电感;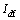 为等效电流;
为等效电流;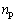 为定子磁极对数;
为定子磁极对数;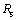 为定子电阻。
为定子电阻。
电磁转矩Te方程和动力平衡方程为:
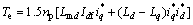 (10)
(10)
 (11)
(11)
式中:Bm为摩擦因数;J为转动惯量;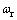 为电机实际转速,由于电机输出轴与油泵输入轴直接连接,因此,
为电机实际转速,由于电机输出轴与油泵输入轴直接连接,因此,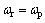 。应用矢量控制的动力方程为
。应用矢量控制的动力方程为
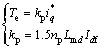 (12)
(12)
式中: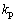 为电磁转矩增益。
为电磁转矩增益。
将式(12)代入式(11),可得
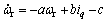 (13)
(13)
式中: ;
;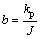 ;
;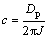 。
。
考虑系统参数变化和外界干扰,上式可改写成
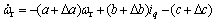 (14)
(14)
式中:△a,△b和△c为电机系统不确定部分。
2.3 活塞杆位移控制器
将AFS活塞杆位移模型改写成典型的n阶SISO非线性系统标准形式[14],即
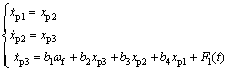 (15)
(15)
式中:xp2与xp3分别为xp1的一阶导数和二阶导数。
位移控制器的目标是通过控制输入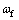 的调节,使AFS活塞杆的位移
的调节,使AFS活塞杆的位移 快速跟踪指令位移
快速跟踪指令位移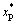 ,定义位移误差信号e1为
,定义位移误差信号e1为
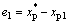 (16)
(16)
分别用e2和e3表示e1的一阶和二阶导数,则有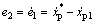 ,
,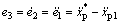 。
。
切换函数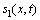 设计为
设计为
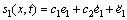 (17)
(17)
式中:c1和c2为滑模控制器参数。
令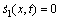 ,并将式(15)代入式(17),得
,并将式(15)代入式(17),得
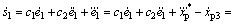
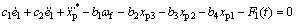 (18)
(18)
等效控制律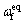 设计为
设计为
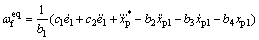 (19)
(19)
为了保证滑模到达条件成立,即
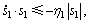 常数
常数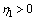 (20)
(20)
设计切换律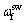 为
为
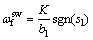 (21)
(21)
式中: 。
。
综合式(19)和式(21),得活塞杆位移控制律 为
为
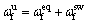 (22)
(22)
2.4 PMSM控制器
电机控制器的设计目的就是找到合适的控制律,使系统输出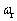 能快速地跟随期望输入
能快速地跟随期望输入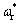 。定义速度误差:
。定义速度误差: 。对其求导得
。对其求导得
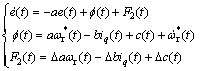 (23)
(23)
式中:iq(t)为定子电流;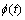 为电流和速度的响应值;a为积分系数;F2(t)为系统干扰及参数变化。
为电流和速度的响应值;a为积分系数;F2(t)为系统干扰及参数变化。
假设满足
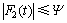 (24)
(24)
式中: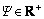 。
。
为减小动态误差,选择积分切换流形面s2:
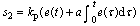 (25)
(25)
式中: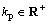 为滑模面增益。
为滑模面增益。
控制律的设计必须保证系统在任意初始状态都能到达滑模态,采用等效控制律设计方法。
对式(25)求导,可得
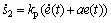 (26)
(26)
将式(23)代入式(26),则
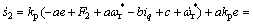
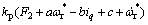 (27)
(27)
考虑没有扰动的情况下(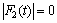 ),令式(27)等于0,可得滑模等效控制律
),令式(27)等于0,可得滑模等效控制律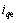 为
为
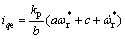 (28)
(28)
采用以下的切换控制律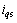 :
:
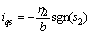 (29)
(29)
式中:常数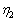 >
>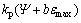 。
。
综合上述式(28)与式(29)得滑模控制律为
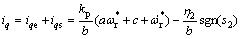 (30)
(30)
由于实际系统执行机构在时间上存在延迟和空间滞后,滑模控制律输出幅值过大的正负高频信号容易产生抖振。设计如下控制律以抑制系统的抖振:
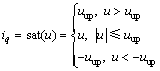 (31)
(31)
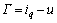 (32)
(32)
式中:uup为边界层值;u为控制器输出电流;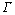 为实际输出电流与控制器输出电流的偏差。为削弱系统产生抖动,需根据系统参数变化和外界干扰对uup进行调节。利用RBF神经网络具有对任意非线性函数的逼近能力在线调整uup。
为实际输出电流与控制器输出电流的偏差。为削弱系统产生抖动,需根据系统参数变化和外界干扰对uup进行调节。利用RBF神经网络具有对任意非线性函数的逼近能力在线调整uup。
神经网络的输入输出如下:
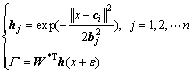 (33)
(33)
式中:x为网络输入的系统速度跟随误差;i为网络输入层的第i个输入;j为网络隐含层第j个网络输入的系统实际速度;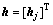 是高斯基函数的输出向量,hj为神经网络的输入向量;ci和bj分别为第j个隐层的中心向量和基宽;向量W*是网络的理想权值;ε为理想神经网络逼近
是高斯基函数的输出向量,hj为神经网络的输入向量;ci和bj分别为第j个隐层的中心向量和基宽;向量W*是网络的理想权值;ε为理想神经网络逼近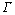 的误差,
的误差,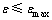 ;
;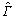 为网络输出的电机在直角坐标下的电流分量;向量
为网络输出的电机在直角坐标下的电流分量;向量 为网络的估计权值。
为网络的估计权值。
选取式(32)中的参数u作为神经网络的输入,即x=u,则神经网络的输出为
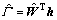 (34)
(34)
取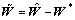 ,则有
,则有
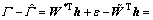
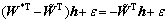 (35)
(35)
因此,控制律式(32)改写为
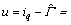
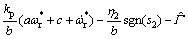 (36)
(36)
2.5 稳定性分析
选取如下Lyapunov函数:
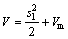 (37)
(37)
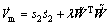 (38)
(38)
针对式(38),将式(32)代入式(27),得
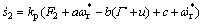 (39)
(39)
将式(36)代入式(39)得
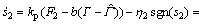
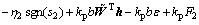 (40)
(40)
将式(40)代入式(38),有
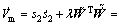
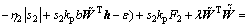
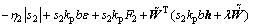 (41)
(41)
设计以下自适应控制律:
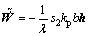 (42)
(42)
则有
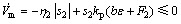 (43)
(43)
将式(22)代入式(19),并结合式(43)和式(37),得
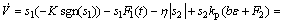
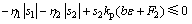 (44)
(44)
系统满足Lyaunov稳定性条件。
3 仿真与结果分析
为验证控制策略的可行性和有效性,利用AMESim和Simlink建立联合仿真模型,如图3所示。根据比例与微分环节,选取滑模控制器参数c1=4 000,c2=10,其他标称参数见表1。
对AFS直接转向干预和变传动比2种工作模式分别进行仿真。
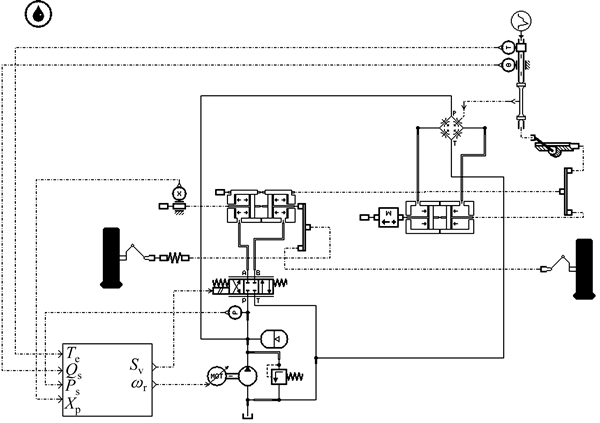
图3 新型电动液压转向系统联合仿真模型
Fig. 3 Co-simulation model of new electro-hydraulic steering system
表1 仿真参数
Table 1 Simulation parameters
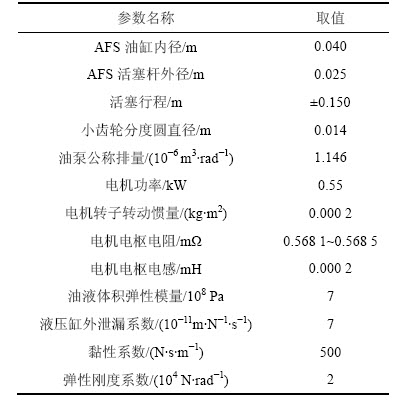
1) 直接转向干预。此模式用于车辆操纵稳定性的主动控制,当车速超过20 m/s时AFS才会动作。主动转角指令一般为阶跃信号,由于轮胎侧偏力具有饱和特性,其叠加的前轮转角不大于5°,由转向系统角传动比可计算出横拉杆位移为10.5 mm。仿真结果如图4~7所示,为进行对比,图中同时给出了传统滑模控制仿真结果。
由图4~7可以看出:2种控制器的动态跟踪性能均较好,且基本相同。稳态误差控制在0.02 mm以内,跟踪精度完全满足转向系统要求,到达指令位移的响应时间小于0.1 s,优于方向盘人工体学转向速度1 r/s的标准。对比表明,传统滑模控制的电机具有抖振现象,系统的压力和流量也产生了脉动,利用神经网络对边界层进行估计与补偿控制后,滑模控制器有效削弱了抖振,提高了系统的稳定性。由于电机速度在活塞杆接近期望位置时快速下降,因而产生了1个压力脉冲。
2) 变传动比模式。实际转向操纵多为斜坡输入,且斜坡信号能更好地表现出系统的动态特性和跟踪精度。不失一般性,针对原地转向时,方向盘以30 r/min匀速正反转动,方向盘转角斜坡信号如图8所示。采用增加1倍的传动比模式,即在2 s内助力活塞杆位移为44 mm,主动活塞杆位移88 mm,仿真结果如图9~12所示。
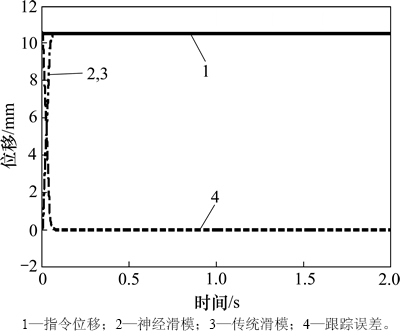
图4 直接转向干预模式下AFS活塞杆位移跟踪曲线
Fig. 4 Displacement tracking curves of AFS piston rod with direct steering intervention mode
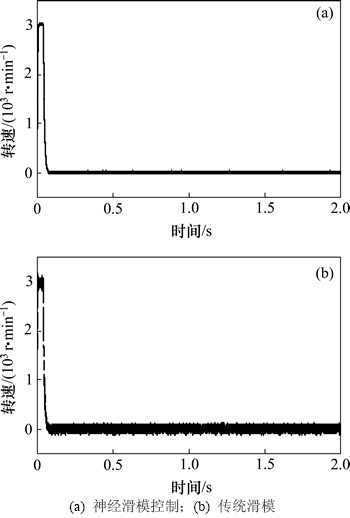
图5 直接转向干预模式下电机泵转速变化曲线
Fig. 5 Speed curves of motor pump with direct steering intervention mode
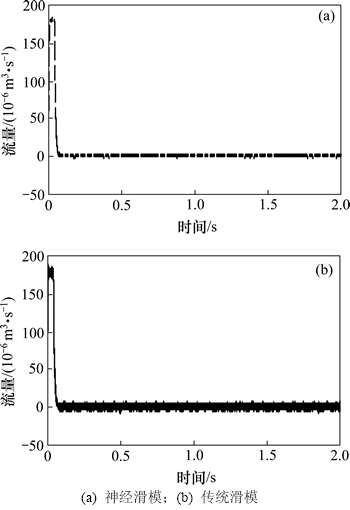
图6 直接转向干预模式下AFS油缸右腔流量变化曲线
Fig. 6 Flow curves of AFS cylinder right cavity with direct steering intervention mode
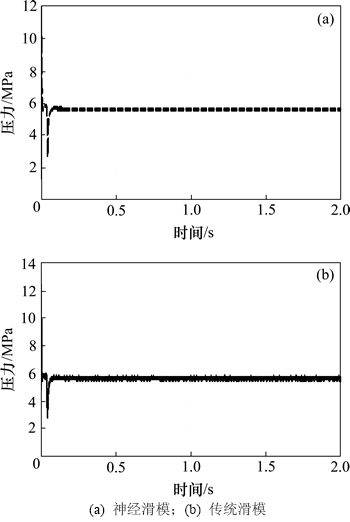
图7 直接转向干预模式下油缸右腔压力变化曲线
Fig. 7 Pressure curves of cylinder right cavity with direct steering intervention mode
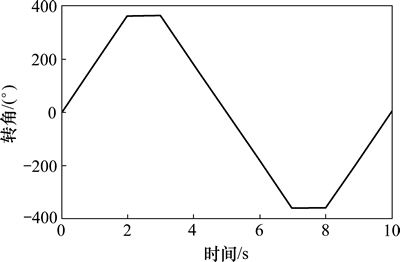
图8 直接转向干预模式下方向盘转角变化曲线
Fig. 8 Angle curve of steering wheel with direct steering intervention mode
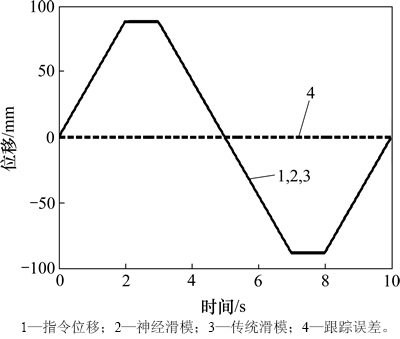
图9 变传动比模式下AFS活塞位移跟踪特性曲线
Fig. 9 Displacement tracking curves of AFS piston rod with variable ratio mode
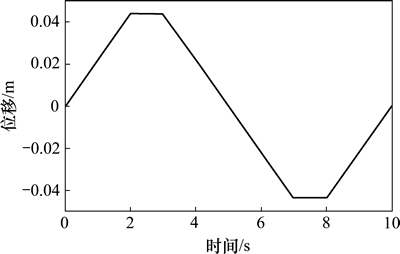
图10 变传动比模式下助力活塞杆位移曲线
Fig. 10 Displacement curve of PS piston rod with variable ratio mode
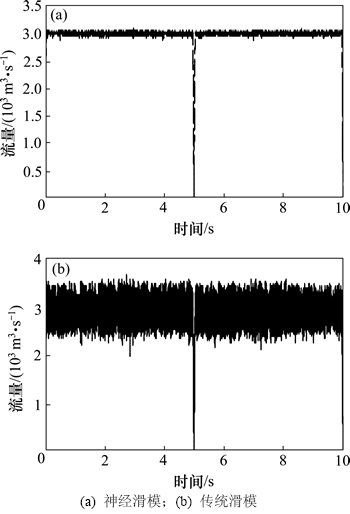
图11 变传动比模式下电动泵转速变化曲线
Fig. 11 Speed curves of motor pump with variable ratio mode
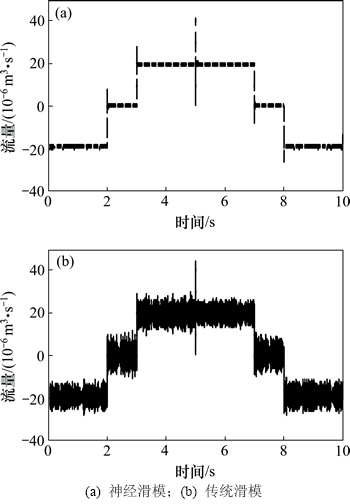
图12 变传动比模式下AFS油缸右腔流量变化曲线
Fig. 12 Flow curves of AFS cylinder right cavity with variable ratio mode
从图9~12可以看出:虽然2种控制器的位移跟踪误差均控制在0.1 mm之内。由于在变传动比工作过程中,助力油缸与主动转向油缸之间既有力的相互作用,又有位移的叠加,是一个动态变化的过程。由仿真结果发现:传统滑模的电机转速产生了±500 r/min高频抖振,并使系统稳态流量脉动达到了±10-5 m3/s。而神经滑模控制器能有效地抑制电机转速的抖振现象,其抖振幅值控制在±30 r/min之内,转速变化曲线平滑,大大改善了系统的综合控制性能。
4 结论
1) 设计了一种新型PMSM直驱齿轮泵容积式电动液压伺服转向系统,利用双伸缩液压缸集成了PS与AFS,方便了对转向力矩与角位移的分工与协同控制,有效提升了转向系统的综合性能指标,为实现汽车转向轻便性、操纵稳定性与主动安全性的协调统一提供了一种可行的解决方案。
2) 针对电动液压位移伺服系统存在参数时变、负载干扰、子系统耦合以及传统滑模的抖振问题,提出了一种双闭环滑模控制算法。联合仿真结果表明:与传统滑模控制方法相比,虽然2种控制器的位移跟踪性能都能满足系统要求,但神经网络滑模控制算法具有更优的动态特性和较强的鲁棒性,有效削弱了传统滑模控制器存在的电机转速严重抖振问题,系统的综合品质得到了明显改善。
3) 无论何种工作模式,转向系统的外负载均为转向阻力,因此,采用匹配与对称结构设计助力转向油缸与主动转向油缸,以满足力与位移耦合控制的一致性,提高了直驱容积式电动液压伺服系统的协同能力。
参考文献:
[1] GUPTE V V, WILLIAMS D, SHERWIN K. Electrically powered hydraulic steering on medium duty truks[J]. SAE International Journal of Commercial Vehicles, 2010, 3(1): 1-8.
[2] ZHAO Wanzhong, SHI Guobiao, LIN Yi. A strategy to enhance the tracking performance of electric power steering system[J]. Chinese Journal of Mechanical Engineering, 2011, 24(4): 585-590.
[3] 王春燕, 崔滔文, 赵万忠, 等. 基于理想传动比的主动前轮转向控[J]. 农业工程学报, 2015, 31(4): 85-90.
WANG Chunyan, CUI Taowen, ZHAO Wanzhong, et al. Active front wheel steering control based on ideal transmission ratio[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(4): 85-90.
[4] 白玉, 桑楠. 基于自抗扰技术的汽车变传动比转向控制[J]. 南京理工大学学报, 2015, 39(4): 452-459.
BAI Yu, SANG Nan. Vehicle variable ratio steering control based on active disturbance rejection technology[J]. Journal of Nanjing University of Science and Technology, 2015, 39(4): 452-459.
[5] 向丹, 迟永滨, 徐炜, 等. 新型主动转向系统的控制及仿真研究[J]. 计算机测量与控制, 2012, 20(9): 2402-2404.
XIANG Dan, CHI Yongbin, XU Wei, et al. Control and simulation of a new active front steering system[J]. Computer Measurement & Control, 2012, 20(9): 2402-2404.
[6] 迟永滨. 一种汽车液压助力主动转向器: CN201110221507.6 [P]. 2012-01-25.
CHI Yongbin. A hydraulic power steering and active steering device of automobile: CN201110221507.6 [P]. 2012-01-25.
[7] 郑宏宇, 王祥, 宗长富, 等. 力控和位置反馈型线控转向系统双向控制策略[J]. 农业机械学报, 2014, 45(6): 9-14.
ZHENG Hongyu, WANG Xiang, ZONG Changfu, et al. Bilateral control strategy of steer-by-wire system using force control and position deviation feedback[J]. Transactions of the Chinese Society Agricultural Machinery, 2014, 45(6): 9-14.
[8] 于蕾艳, 吴宝贵, 伊剑波. 汽车线控转向系统转向控制研究[J]. 江苏大学学报(自然科学版), 2014, 35(3): 267-273.
YU Leiyan, WU Baogui, YI Jianbo. Survey on steering control of automobile steer by wire system[J]. Journal of Jiangsu University(Nature Science Edition), 2014, 35(3): 267-273.
[9] YANG Xiujian, WANG Zengcai, PENG Weili. Coordinated control of AFS and DYC for vehicle handling and stability based on optimal guaranteed cost theory[J]. Vehicle System Dynamics, 2009, 47(1): 57-79.
[10] TJONNAS J, JOHANSEN T A. Stabilization of automotive vehicles using active steering and adaptive brake control allocation[J]. IEEE Transactions on Control Systems Technology, 2010, 18(3): 545-558.
[11] MCCANN R, LE A. Gain schduling control in commercial vehicle with electrohydraulic steering[J]. SAE International Journal of Commercial Vehicles, 2009, 1(1): 481-487.
[12] 宋健, 吕连杰, 禤文伟, 等. 蓄能式商用车电动液压助力转向系统[J]. 清华大学学报(自然科学版), 2014, 54(9): 1209-1214.
SONG Jian, L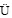 Lianjie, XUAN Wenwei, et al. Electro-hydraulic power steering system for commercial vehicle[J]. Journal of Tsinghua University(Science and Technology), 2014, 54(9): 1209-1214.
Lianjie, XUAN Wenwei, et al. Electro-hydraulic power steering system for commercial vehicle[J]. Journal of Tsinghua University(Science and Technology), 2014, 54(9): 1209-1214.
[13] ZHAO Wanzhong, ZHAO Ting, LI Yijun, et al. Integration optimization of novel electric power steering system based on quality engineering theory[J]. Journal of Central South University, 2013, 20(6): 1519-1526.
[14] 王洪斌, 王思文, 王跃灵, 等. 直驱式液压伺服系统建模及变增益滑模控制[J]. 电机与控制学报, 2013, 17(11): 110-116.
WANG Hongbin, WANG Siwen, WANG Yueling, et al. Modeling and variable gain sliding mode control for a direct drive hydraulic servo system[J]. Electric Machines and Control, 2013, 17(11): 110-116.
[15] 刘军龙, 姜继海, 欧进萍, 等. 直驱容积控制电液伺服系统模型与动态特性[J]. 哈尔滨工业大学学报, 2011, 43(7): 61-65.
LIU Junlong, JIANG Jihai, OU Jinping, et al. Theoretical model and dynamic performance of direct drive volume control electro-hydraulic servo system[J]. Journal of Harbin Institute Technology, 2011, 43(7): 61-65.
[16] GUO Kai, WEI Jianhua, TIAN Qiyan. Nonlinear adaptive position tracking of an electro-hydraulic actuator[J]. Journal of Mechanical Engineering Science, 2015, 229(17): 3252-3265.
[17] 李元春, 王蒙, 盛立辉, 等. 液压机械臂基于反演的自适应二阶滑模控制[J]. 吉林大学学报(工学版), 2015, 45(1): 193-201.
LI Yuanchun, WANG Meng, SHENG Lihui, et al. Adaptive second order sliding mode control for hydraulic manipulator based on backstepping[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(1): 193-201.
[18] 刘金锟. 滑模变结构控制Matlab仿真[M]. 2版. 北京: 清华大学出版社, 2012: 4-5.
LIU Jinkun. Sliding mode control design and Matlab simulation[M]. 2nd ed. Beijing: Tsinghua Press, 2012: 4-5.
[19] 王军, 陈勇. 基于AMESim的电动液压助力转向系统的仿真研究[J]. 盐城工学院学报(自然科学版), 2012, 23(4): 53-57.
WANG Jun, CHEN Yong. Simulation studies of electro hydraulic power steering based on AMESim[J]. Journal of Yancheng Institute of Technology(Natural Science Edition), 2012, 23(4): 53-57.
[20] KEMMETMULLER W, FAUSTNER D, KUGI A, et al. Optimal torque control of permanent magnet synchronous machines using magnetic equivalent circuits[J]. Mechatronics, 2015, 32: 22-33.
(编辑 刘锦伟)
收稿日期:2015-09-21;修回日期:2015-12-05
基金项目(Foundation item):国家自然科学基金资助项目(61105085);江西省科技厅资助项目(20123BBE50085) (Project(61105085) supported by the National Natural Science Foundation of China; Project(20123BBE50085) supported by the Project of Department of Science and Technology of Jiangxi Province)
通信作者:黄开启,博士,副教授,从事机电液系统设计、汽车动力学与控制研究;E-mail: kaiqi.huang@163.com