考虑交通管理策略的交叉口信号控制多目标优化
龙琼1, 2,胡列格2,张谨帆1,周昭明1,彭烁2
(1. 湖南城市学院 土木工程学院,湖南 益阳,413000;
2. 长沙理工大学 交通运输工程学院,湖南 长沙,410004)
摘要:面向复杂多变的交通系统控制需求,提出一种考虑交通管理策略的交叉口信号控制多目标优化模型及算法,其步骤为:首先,构建城市道路交叉口多目标优化模型;然后,引入交通管理者的交通控制策略,基于模糊分析法确定各优化指标权重;最后,考虑Q学习算法简单方便且具有快速收敛性,基于Q学习算法对多目标优化模型进行求解,从而实时产生考虑交通管理者策略的交叉口信号控制方案。仿真结果表明,所提出的方法不仅能够充分反映交通管理者的控制策略,而且能够有效提高交叉口通行效率,相比传统方法具有缩短排队长度、降低延误时间和减少停车次数的优势,并且这种优势随着交通流量的增大而更加明显。
关键词:多目标优化;交通管理策略;交叉口;信号控制;模糊分析法;Q学习算法
中图分类号:U491.4 文献标志码:A 文章编号:1672-7207(2014)07-2503-06
Multi-objective optimization based on traffic management strategy for intersection signal controlling
LONG Qiong1, 2, HU Liege2, ZHANG Jinfan1, ZHOU Zhaoming1, PENG Shuo2
(1. School of Civil Engineering, Hunan City University, Yiyang 413000, China;
2. School of Traffic and Transportation, Changsha University of Science & Technology, Changsha 410004, China)
Abstract: A multi-objective optimization model and its algorithm aimed at the intricate demand of traffic system controlling were presented. The procedures were as follows. The traffic controlling strategy was drawn into the model after the model was built. The weight of optimization index was determined based on fuzzy analytic process. The solutions of the multi-objective optimization model were obtained by Q-algorithm, based on the fact that the Q-algorithm is fast constrained and convenient. The program of intersection signal controlling based on traffic management strategy was real-time produced. The simulation results show that the method can not only fully reflect the control strategies of traffic managers, but also improve the travelling efficiency at intersection. Compared with the traditional method, it has some advantages such as the queue length shortened, the time delayed and the number of parking reduced. These advantages are more obvious with the increase of the traffic flow.
Key words: multi-objective optimization; traffic controlling strategy; intersection; signal controlling; fuzzy analytic process; Q-algorithm
随着城市人口数量的不断增长和人们物质生活水平的逐渐提高,机动车保有量迅猛增长,进而使道路交通需求急剧增加,交通拥堵问题日益凸显。针对交通拥堵问题,仅仅通过加强交通基础设施的建设是难以解决的,而根据实际交通状况实时优化交通信号控制方案是一种有效缓解交通拥堵的手段。交叉口作为城市交通网络中的重要组成部分,是城市交通拥挤的主要发生地,所以,针对城市道路交叉口交通信号控制问题开展研究,对于改善城市道路交通拥堵状况、提高道路通行能力、减少交通事故、减少交通环境污染等方面具有十分重要的现实意义。交通信号控制是调控路网交通流运行的主要交通管理措施之一,应体现安全、通畅、高效等多方面的控制意图[1]。在优化交通信号协调控制参数时,需要考虑交通管理策略,权衡平均延误时间、排队长度、通过流量等指标[2-3],因此,交通信号控制问题是一个考虑交通管理策略的多目标优化问题。近年来,采用多目标优化方法研究城市道路交通信号控制问题已成为研究热点。早期的多目标优化是Akcelik[4]在F-B 法的基础上引入停车补偿系数,结合车辆延误时间参数,共同评价信号配时的优化程度。Vincent等[5]以TRANSYT 系统为对象,将延误时间和停车次数转换为燃油消耗指标,基于爬山法和遗传算法对模型求解。常健等[6]建立了车辆排队延误和路段行程时间的加权线性组合优化模型,求解获得控制参数,并定性地探讨了权重系数与优化目标之间的变化关系。Zeng等[7]基于元胞传输模型,模拟车流在道路交叉口的运行规律,建立了以平均延误和通行能力为优化目标的多目标优化模型,采用MOGA多目标遗传算法进行了模型求解。曹成涛等[8]引入交通控制饱和度约束,建立了以机动车流的平均延误、平均停车次数和总通过流量为优化目标的加权组合优化模型,基于遗传算法对模型进行求解。高云峰等[1]以交叉口群为对象,建立了交通信号协调控制参数的多目标优化模型,基于非支配排序遗传算法设计了相应的多目标优化算法求解模型。但是,由于实际交通系统的复杂性和多变性,交通状况难以精确描述,多目标优化模型往往通过简单加权来转化为单目标优化模型进行求解,忽略了交通管理者对交通流疏导的策略和意图,因而,这类多目标优化模型往往难以适应实际复杂多变的城市道路交通系统控制需求。为此,本文作者面向复杂多变的交通系统控制需求,充分考虑交通管理者对交通疏导的控制策略,基于模糊分析法(fuzzy analytic process,FAP)设计了一种城市道路交叉口信号控制多目标优化模型,同时,考虑Q学习算法具有快速收敛特性的同时,无需过多顾及环境指标的动态变化,基于Q学习算法对多目标优化模型进行求解,从而实时产生考虑交通管理者策略的交叉口信号控制方案。
1 基于FAP的多目标优化模型
1.1 交叉口优化模型
交叉口交通信号控制优化模型的评价指标一般为单位时间内通过的车流量最大、车辆总延误时间最短、车辆排队长度最短、车辆在交叉路口的平均停车次数最少等,控制模型根据交通控制目标构造评价函数,结合交通管理者的控制意图,对交叉口进行优化控制。以典型的平面十字交叉城市道路口为例,本文选用排队长度l、延误时间d和停车次数n作为模型优化评价指标,构建综合评价指标函数为
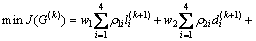
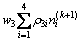 (1)
(1)
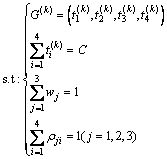
式中:G(k)表示第k个控制周期内的控制函数,即四相位绿灯时长分别为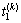 ,
,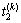 ,
,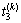 ,
,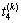 ;C为控制周期时长;
;C为控制周期时长;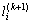 为第k+1个控制周期开始时的第i相位的车辆排队长度;
为第k+1个控制周期开始时的第i相位的车辆排队长度;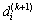 为第k+1个控制周期开始时第i相位排队车辆的平均延误时间;
为第k+1个控制周期开始时第i相位排队车辆的平均延误时间;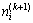 为第k+1个控制周期开始时的第i相位排队车辆的平均停车次数;wj为第j个指标在综合评价指标函数中的权重;
为第k+1个控制周期开始时的第i相位排队车辆的平均停车次数;wj为第j个指标在综合评价指标函数中的权重;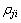 为第j个指标在第i个相位的权重。
为第j个指标在第i个相位的权重。
值得说明的是:在模型(1)中,排队长度l、延误时间d和停车次数n的量纲不同,在实际操作过程中,需要经过统一归一化处理。同时,在模型中,w j和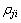 体现了交通管理者对指标和相位的重视程度,而交通管理者的认识本身具有主观性和模糊性,增加了模型求解的复杂程度。本文考虑引入模糊分析法(FAP)对这些权重系数进行量化,从而简化交通管理者判断交通优化指标相对重要性的复杂过程,解决交通指标优化排序过程中的一致性问题,使优化模型更好地反映交通管理者的控制需求。
体现了交通管理者对指标和相位的重视程度,而交通管理者的认识本身具有主观性和模糊性,增加了模型求解的复杂程度。本文考虑引入模糊分析法(FAP)对这些权重系数进行量化,从而简化交通管理者判断交通优化指标相对重要性的复杂过程,解决交通指标优化排序过程中的一致性问题,使优化模型更好地反映交通管理者的控制需求。
1.2 基于FAP的权重系数确定
实际问题往往具有复杂性和模糊性,用模糊数表示判断的结果能够更好地反映事物的客观本质。因此,本文在权重确定过程中引入模糊数学理论,即应用模糊分析法对交通优化模型进行权重确定。与一般方法相比,模糊分析法简化了人们判断评价相对重要性的复杂程度,解决了权重确定过程中的一致性问题。
基于模糊分析法进行权重确定的基本过程是[9-10]:在构建交叉口优化模型的基础上,以矩阵形式表达各单项优化指标的相对重要性,从而建立相应的模糊矩阵:
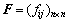 (2)
(2)
其矩阵元素按如下的模糊逻辑确定:
 (3)
(3)
对模糊矩阵F进行一致化处理,构成模糊一致矩阵:
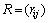 (4)
(4)
其中,rij按照如下方式确定:
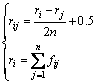 (5)
(5)
然后进行权重确定,即根据模糊一致矩阵计算对于交通管理者而言的指标重要性相对权重(不含自身比较):
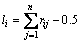 (6)
(6)
进行归一化后可得
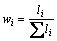 (7)
(7)
基于上述思想,对于交叉口优化模型(1),交通管理者根据交通管理策略,仅需确定排队长度l、延误时间d和停车次数n等指标的相对重要性,就可确定相应的指标权重wj (j=1, 2, 3)。同理,对于各优化指标在不同相位的权重系数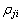 ,亦可以通过类似方法确定,由此可以看出:基于模糊分析方法,交通管理者仅需两两比较优化指标的相对重要性,大大降低了交通管理者根据自身意图来设置指标权重的复杂程度,且该方法还能够有效保证权重确定过程中的一致性问题。
,亦可以通过类似方法确定,由此可以看出:基于模糊分析方法,交通管理者仅需两两比较优化指标的相对重要性,大大降低了交通管理者根据自身意图来设置指标权重的复杂程度,且该方法还能够有效保证权重确定过程中的一致性问题。
2 基于Q学习的模型优化
2.1 Q学习算法
Q学习算法最早在1989年由Watkins等提出[11],是模拟动物学习行为的一种强化学习算法,该算法因操作简单且收敛性好而受到研究者的重视。Q学习算法通过从环境中得到奖惩的方法来获得不同状态下的最优策略。Q学习的积累回报函数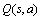 是指在状态s执行完动作a后希望获得的积累回报,它取决于当前的立即回报和期望的延时回报。
是指在状态s执行完动作a后希望获得的积累回报,它取决于当前的立即回报和期望的延时回报。
在Q学习算法中,模型通过不断反射学习优化1个可以迭代计算的Q函数提高学习能力,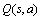 函数的初始值可任意给定,其学习规则为[12]
函数的初始值可任意给定,其学习规则为[12]
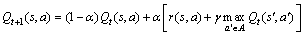 (8)
(8)
式中: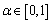 为学习速率;
为学习速率;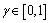 为折扣因子;a为所有可供选择的动作的集合;
为折扣因子;a为所有可供选择的动作的集合;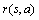 为回报函数值;
为回报函数值;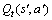 为在下一个状态s’时系统选择任何行为
为在下一个状态s’时系统选择任何行为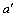 的Q函数值。
的Q函数值。
Q学习算法不同于其他学习算法[13]的是不需要建立面向外部状态环境变化的模型,适合于在线学习。近年来,Q学习在人工智能、机器学习等领域取得了诸多研究成果,在此,本文采用Q学习算法用于求解交叉口的信号控制优化问题。
2.2 基于Q学习的交叉口模型优化
根据交叉口模型(1),控制参数集和决策参数集可以分别表达为:
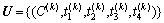 (9)
(9)
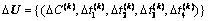 (10)
(10)
其中: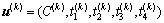 为第k个周期的控制向量;
为第k个周期的控制向量;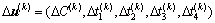 (满足约束条件
(满足约束条件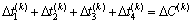 )为第k个周期的决策向量;
)为第k个周期的决策向量;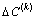 ,
,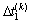 ,
,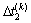 ,
,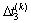 和
和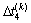 分别为第k个周期的控制周期时长改变量和各相位绿灯时间改变量。在一般情况下,控制周期时长固定,即
分别为第k个周期的控制周期时长改变量和各相位绿灯时间改变量。在一般情况下,控制周期时长固定,即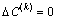 ,则控制参数
,则控制参数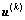 和决策参数
和决策参数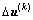 可简化为:
可简化为:
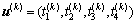 (11)
(11)
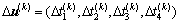
(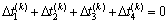 ) (12)
) (12)
同时,在实际交通信号控制中,信号灯时间通常以秒(s)为单位计时,因而,控制参数集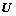 和决策参数集
和决策参数集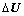 均为有限可数集合。这给Q学习算法的应用带来了方便。
均为有限可数集合。这给Q学习算法的应用带来了方便。
根据模型(1),设计收益函数如下:
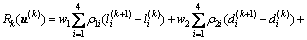
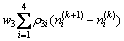 (13)
(13)
在权重系数wj和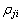 确定后,下面参照文献[14]并作以改进,设计获得相应的交通信号控制策略。
确定后,下面参照文献[14]并作以改进,设计获得相应的交通信号控制策略。
2.2.1初始控制参数
初始控制参数的确定依据
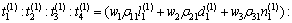
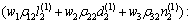
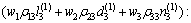
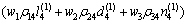 (14)
(14)
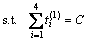
求解相应的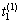 ,
,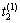 ,
,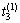 ,
,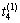 ,从而获得相应的
,从而获得相应的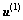 。
。
2.2.1 过程控制策略
在第k+1个周期个控制周期,控制策略设计如下。
(1) 若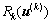 <0,则说明控制系统趋于收敛,交通状况渐趋通畅,
<0,则说明控制系统趋于收敛,交通状况渐趋通畅,
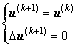 (15)
(15)
(2) 若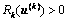 ,则说明控制系统趋于发散,交通状况渐趋恶化。令
,则说明控制系统趋于发散,交通状况渐趋恶化。令
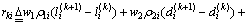
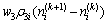 (16)
(16)
若对所有相位i=1, 2, 3, 4,均有rki>0,则说明交通流量逐渐增大而导致交通系统整体恶化,此时,重新调整控制策略,依据下式
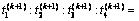
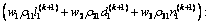
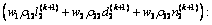
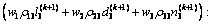
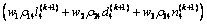 (17)
(17)
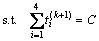
求解相应的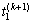 ,
,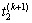 ,
,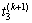 和
和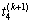 ,从而获得相应的
,从而获得相应的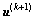 和
和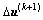 。
。
若控制系统只在部分相位恶化,而在其他相位有向好的趋势,记趋势向好的相位集合为A,其他相位集合为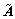 ,则对于有
,则对于有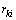 <0(
<0(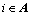 )的相位,
)的相位,
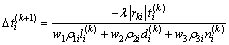 (18)
(18)
式中: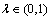 为保守因子。记
为保守因子。记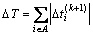 ,则对于其他相位(
,则对于其他相位(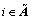 ),有
),有
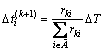 (19)
(19)
由此获得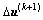 ,从而可求得第k+1个周期的控制量
,从而可求得第k+1个周期的控制量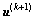 。与文献[14]相比,本文在此引入了保守因子
。与文献[14]相比,本文在此引入了保守因子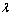 ,避免了对交通恶化相位的过度反应,保证了渐趋通畅相位的收敛性。
,避免了对交通恶化相位的过度反应,保证了渐趋通畅相位的收敛性。
(3) 若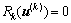 ,则说明交通整体状况没有发生变化,此时,对应的交叉口交通状况是:部分相位恶化,部分相位向好(理论上存在所有相位交通状况均没有变化的情况),参照情况(2)进行研究微调。
,则说明交通整体状况没有发生变化,此时,对应的交叉口交通状况是:部分相位恶化,部分相位向好(理论上存在所有相位交通状况均没有变化的情况),参照情况(2)进行研究微调。
3 实验仿真
为了验证本文方法的有效性,以典型的十字交叉路口为例,针对如下2种想定情况进行仿真实验,并与传统的定时控制方法进行对比。
(1) 情况1:不考虑交通管理策略。
在不考虑交通控制策略的情况下,交通管理者对各优化指标和相位无偏好,因此,在模型(1)中,权重系数取值为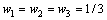 ,
,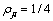 ( j=1, 2, 3; i=1, 2, 3, 4)。
( j=1, 2, 3; i=1, 2, 3, 4)。
(2) 情况2:考虑交通管理策略。
假设交通管理者面向大区域交通系统需求,设置其优化指标的相对重要性为:排队长度相对重要性>延误时间相对重要性=停车次数相对重要性。
同时,大区域交通环境要求优先保障处于第1和第2相位的车辆通过,同时兼顾第3和第4相位车辆,则相位相对重要性设置为:第1相位相对重要性=第2相位相对重要性>第3相位相对重要性=第4相位相对重要性。
根据前面的权重系数确定方法,求得
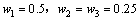
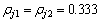 ,
,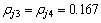 ;j=1, 2, 3
;j=1, 2, 3
取控制周期C=120 s,保守因子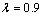 ,在不同交通流量下获得的仿真结果如图1~3所示。
,在不同交通流量下获得的仿真结果如图1~3所示。
从图1~3可以看出:本文所提出的多目标优化控制算法能够较大幅度地缩短排队长度、延误时间和减少停车次数,与传统定时控制方法相比具有明显的优势,这种优势随着交通流量的增大更加明显。
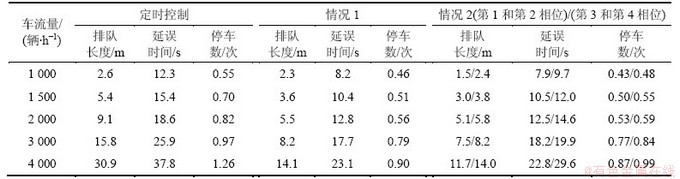
表1所示为各种控制模型的各种具体控制结果。从表1可以看出:在不同车流量条件下,采用本文方法能够有效减小排队长度、延误时间和停车次数,大大提高了交通系统的运行效率。特别地,根据情况2获得的实验结果,与第3和第4相位相比,第1和第2相位更加通畅,尤其是在不同车流量下,第1和第2相位的排队长度较短,较好地体现了交通管理者的控制意图。
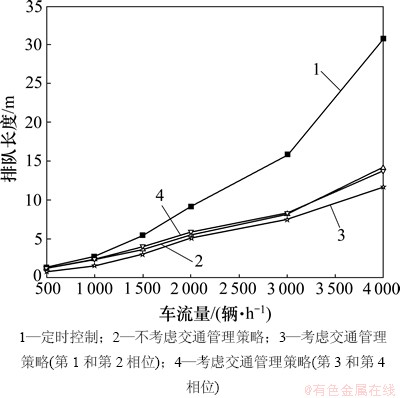
图1 不同车流量条件下的排队长度对比
Fig. 1 Comparison of queue length at different traffic conditions
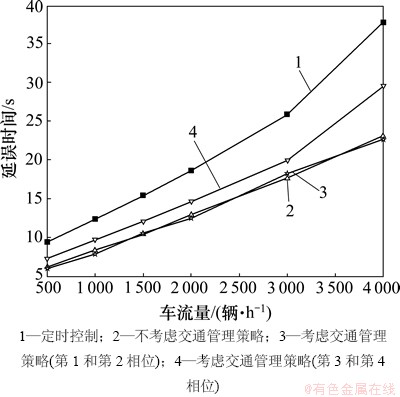
图2 不同车流量条件下的延误时间对比
Fig. 2 Comparison of delay time at different traffic conditions
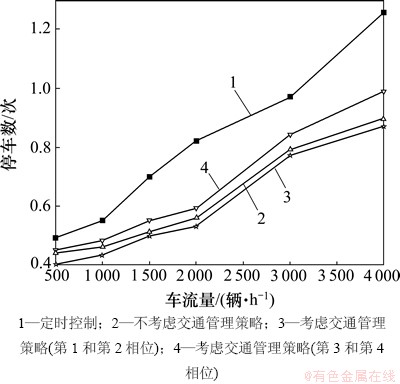
图3 不同车流量条件下的停车次数对比
Fig. 3 Comparison of number of parking at different traffic conditions
表1 不同车流量条件下的仿真结果比较
Table 1 Comparision of simulation results at different traffic conditions
4 结论
面向复杂多变的交通系统控制需求,基于模糊分析法设计了一种城市道路交叉口信号控制多目标优化模型,并基于Q学习算法对多目标优化模型进行求解,该方法具有如下特点:
(1) 在建模过程中,充分考虑了交通管理者对交通疏导的控制策略,有利于保持与大区域交通环境的一致性。
(2) 引入模糊分析法确定优化指标权重系数,简化了人们判断评价相对重要性的复杂程度,解决了权重确定过程中的一致性问题。
(3) 构建了交叉口多目标最优模型,克服了以往优化方法目标单一的缺点。仿真结果表明该模型能够兼顾多种优化指标,获得折中解。
(4) 基于Q学习算法对多目标优化模型进行求解,简化了求解过程,保证了求解结果的收敛性。
参考文献:
[1] 高云峰, 胡华, 韩皓, 等. 城市道路交叉口群信号协调控制多目标优化与仿真[J]. 中国公路学报, 2012, 25(6): 129-135.
GAO Yunfeng, HU Hua, HAN Hao. Multi-objective optimization and simulation of groups of intersections’ signal coordinate control[J]. China Journal of Highway and Transport, 2012, 25(6): 129-135.
[2] DAI Yujie, ZHAO Dongbin. A traffic signal control algorithm for isolated intersections based on adaptive dynamic programming[C]// Proceedings of 2010 International Conference on Networking, Sensing and Control (ICNSC 2010). Chicago, USA, 2010: 255-260.
[3] Abdulhai B. Reinforcement learning for true adaptive traffic signal control[J]. ASCE Journal of Transportation Engineering, 2003, 129( 3) : 278-285.
[4] Akcelik R. Traffic signals: Capacity and timing analysis, ARR No.123[R]. Vermont South, Australia: ARRB Transport Research Ltd, 1981: 26-29.
[5] Vincent R A, Mitchell A I, Robertson D I. User guide of transport, Version 8, TRRL Report LR888[R]. Crowthorne, UK: Transport and Road Research Labortory, 1980: 356-361.
[6] 常健, 吴大为. 多目标交叉口信号控制模型[J]. 大连理工大学学报, 2000, 40(6): 653-656.
CHANG Jian, WU Dawei. Multi-objective model of intersection signal control[J]. Journal of Dalian University of Technology, 2000, 40(6): 653-656.
[7] Zeng J Q, Wang J J, Liu K, et al. CTM-MOGA based crossroad traffic signal control[J]. Journal of University of Science and Technology of China, 2005, 35(2): 284-290.
[8] 曹成涛, 徐建闽. 单交叉口交通多目标控制方法[J]. 计算机工程与应用, 2010, 46(16): 20-22.
CAO Chengtao, XU Jianmin. Multi-objective control method at single intersection[J]. Computer Engineering and Applications, 2010, 46(16): 20-22.
[9] XU Runing, ZHAI Xiaoyan. Extention of the analytic hierarchy process in fuzzy environment[J]. Fuzzy Sets and Systems, 1992, 52: 29-32.
[10] 汪培庄. 模糊集合论及其应用[M]. 上海: 上海科学技术出版社, 1986: 329-332.
WANG Peizhuang. Fuzzy set theory and its applications[M]. Shanghai: Shanghai Science and Technology Press, 1986: 329-332.
[11] Watkins C, Dayan P. Technical note: Q-learning machine learning[M]. Kluwer Academic Publishers, Boston, 1992: 279-292.
[12] 魏赟, 邵清. 基于Q-学习和粒子群算法的区域交通控制模型[J]. 系统仿真学报, 2011, 23(10): 2108-2111.
WEI Yun, SHAO Qing. Regional traffic control model based on Q-learning and particle swarm optimization[J]. Journal of System Simulation, 2011, 23(10): 2108-2111.
[13] 席燕辉, 叶志成, 彭辉. 一种基于自适应粒子滤波的多层感知器学习算法[J]. 中南大学学报(自然科学版), 2013, 44(4): 1397-1402.
XI Yanhui, YE Zhicheng, PENG Hui. An algorithm for MLPs training based on adaptive particle filter[J]. Journal of Central South University (Science and Technology), 2013, 44(4): 1397-1402.
[14] 崔吉峰, 乞建勋, 杨尚东. 基于粒子群改进BP神经网络的组合预测模型及其应用[J]. 中南大学学报(自然科学版), 2009, 40(1): 190-194.
CUI Jifeng, QI Jianxun, YANG Shangdong. Combined forecasting model based on BP improved by PSO and its application[J]. Journal of Central South University (Science and Technology), 2009, 40(1): 190-194.
[15] 马跃峰, 王宜举. 一种基于Q学习的单路口交通控制方法[J]. 数学的实践与认识, 2011, 41(24): 102-106.
[16] MA Yuefeng, WANG Yiju. A traffic control method for single intersection based on Q-learning algorithm[J]. Mathematics in Practice and Theory, 2011, 41(24): 102-106.
(编辑 陈灿华)
收稿日期:2013-09-10;修回日期:2014-11-25
基金项目:国家自然科学基金资助项目(51278068);湖南省科技厅资助项目(2012GK3069);湖南省自然科学基金资助项目(07jj6093)
通信作者:龙琼(1967-),女,湖南长沙人,长沙理工大学访问学者,硕士,高级工程师,从事交通管理与控制研究;电话:0737-4628998;E-mail: longqiong@126.com