Microstructures and hardness of Ti-6Al-4V alloy staging castings under centrifugal field

SUI Yan-wei(隋艳伟)¹, LI Bang-sheng(李邦盛)¹, LIU Ai-hui(刘爱辉)¹,

NAN Hai(南 海)², GUO Jing-jie(郭景杰)¹, FU Heng-zhi(傅恒志)¹

1. School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China

2. Beijing Institute of Aeronautical Materials, Beijing 100095, China

Received 10 May 2007; accepted 13 September 2007

Abstract: By means of induction melting technology, Ti-6Al-4V alloy staging casting was made with the same rotation velocity and centrifugal radius. The effects of casting modulus on the grain size, the thickness of lamellar α+β phase, and the Vickers hardness, as well as the relationships between Vickers hardness, grain size and thickness of lamellar α+β phase were investigated. The results show that the greater the modulus, the larger the grain size and the thickness of lamellar α+β phase, and the less the Vickers hardness. The relationship between Vickers hardness and grain size meets the Hall-Petch equation: Hv=353.45+74.17. The relationship between the Vickers hardness and the thickness of lamellar α+β phase is expressed as Hv=

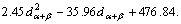
Key words: Ti-6Al-4V alloy; centrifugal field; modulus; microstructure; hardness

1 Introduction

Ti-6Al-4V alloy is the typical two-phase titanium alloy with the most extensive and mature application. For its low density, high specific modulus and strength, excellent corrosion resistance and creep resistance[1-5], Ti-6Al-4V alloy has got the wide applications in spaceflight, aviation, and biomedicine fields where special structural components are urgently needed. These special structure components are not only complex in structures and shapes, but also strict in requirements for microstructure and mechanical property. However, Ti-6Al-4V alloy is prone to generate porosity because of its high chemical reactivity and poor flowability at high temperature. In order to significantly increase the filling and feeding ability of liquid metal during the solidification, decrease shrinkage cavity, shrinkage porosity, and porosity to obtain sound castings with high density, enhance freezing rate to make castings obtain excellent microstructure and mechanical properties which can not obtained in the gravity field, Ti-6Al-4V alloy must be poured and shaped in the centrifugal field [6-12].

Up to now, studies on the solidified structures and properties of Ti-6Al-4V alloy mainly focus on the conventional gravity field[13-14], and little research has been done on the centrifugal field. Meanwhile, the special structure components for practical application have different wall thicknesses, resulting in considerable changes of modulus and cooling velocity. Thus under the centrifugal field, the study on the microstructure and property of Ti-6Al-4V alloy in the different cooling velocities is the important base to the effective application of titanium alloy. Therefore, this work aims to study the effects of casting modulus on microstructure and hardness of Ti-6Al-4V alloy staging castings under the centrifugal field, and the relationship between microstructure and hardness so as to further optimize microstructure and property of Ti-6Al-4V alloy.

2 Experimental

The experimental materials are pure Al, commercial pure Ti, and Al-V intermediate alloy. Ti-6Al-4V alloy was prepared by means of the vacuum induction melting technology. The vacuum degree was 0.1 Pa, the power was 350 kW, and the preheating temperature of ceramic mould was 200 ℃. Under the centrifugal force, the liquid Ti-6Al-4V alloy was poured into the ceramic mould from the bottom, with the rotation velocity of 220 r/min, and centrifugal radius of 500 mm. Fig.1 shows the apparatus used to conduct experiment. The staging sample is shown in Fig.2.

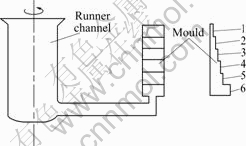
Fig.1 Schematic diagram of experimental apparatus

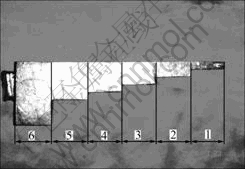
Fig.2 Centrifugal staging castings

Specimens were cut from six positions of Ti-6Al-4V alloy staging casting, as shown in Fig.2. The dimension of the specimens is 20 mm×20 mm×6 mm. The specimens preparation for metallographic observation included grinding using SiC papers from 220 up to 1200 grit, diamond paste polishing, ultrasonic cleaning for 5 min, and etching (2%HF-2%HNO₃-H₂O, volume fraction). An optical microscope (OLYMPUS BH2-UMA) was used for the real-time observation of the specimens. On the basis of the transversal method, the grain sizes were measured by the optical microscope. By means of a scanning electron microscopy (S-4700SEM), the microstructures were analyzed and the thicknesses of laminar α+β phase were measured. In addition, the average Vickers hardnesses of six specimens with different modulus were investigated in a microhardness tester. Testing load was 0.98 N, and loading duration was 15 s. At the same time, based on the modulus equal to the ratio of liquid metal to radiating surface area, the modulus for six positions was calculated. The radiating surface area for every position is the contact area between liquid metal and mould, which does not include the contact area among six positions.

3 Results and discussion

3.1 Effect of modulus on microstructure

In Fig.3, optical micrographs of six specimens are presented and their grain sizes d_G are measured by means of the transversal method. Fig.4 shows the SEM images of six specimens and the thicknesses of the laminar α+β phases, d_α+β, at six specimens are measured. The grain sizes, modulus, and d_α+β of six specimens are listed in Table 1.

Fig.3 Metallographs of specimens with different modulus: (1) 2.2 mm; (2) 3.7 mm; (3) 4.8 mm; (4) 5.7 mm; (5) 6.3 mm; (6) 8.0 mm

Table 1 Grain size and thickness of lamellar α+β phase of specimens with different modulus

Fig.4 SEM images of specimens with different modulus: (1) 2.2 mm; (2) 3.7 mm; (3) 4.8 mm; (4) 5.7 mm; (5) 6.3 mm; (6) 8.0 mm

The relationship between casting modulus and grain size obtained from the data listed in Table 1 is presented in Fig.5. By polynomial fitting, the relationship between casting modulus M and grain size d_G can be expressed:

d_G=2.625-8.205exp(-0.617M)                   (1)

Fig.5 Relationship between grain size and modulus

Similarly, Fig.6 shows the relationship between the thickness of α+β phase, d_α+β, and modulus, M, which can be extended as follows:

d_α+β=2.87-6.982exp(-0.552M)                  (2)

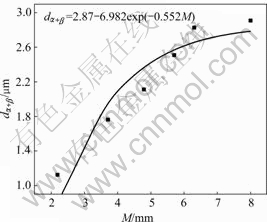
Fig.6 Relationship between thickness of α+β phase and modulus

From Eqns.(1) and (2), it can be noted that the grain size and thickness of α+β phase increase with increasing casting modulus. The variations of grain size at six positions of Ti-6Al-4V casting can be explained thermodynamically and kinetically. From thermo- dynamic viewpoint, as the specimen has small modulus, the cooling velocity is great, and the degree of supercooling of the alloy melt is also great, resulting in the high nucleation rate and nucleating density. From the kinetic aspect, from Ref.[15], the relationship between freezing time and modulus is

t=CM²                                      (3)

where  C is proportion factor, M is modulus, t is freezing time. From Eqn.(3), it can be seen that the smaller the modulus, the shorter the freezing time. Therefore, when the modulus is small, the growing time for every grain is short, and the grain was difficult to grow up. In addition, the grain number increases owing to thermodynamic factor, and the competitive level of liquid atoms rises. The co-action of the above two aspect factors makes the grain size increase with the modulus.

For Ti-6Al-4V alloy staging casting, the phase transformation from β phase to α+β phase belongs to solid-state phase change and the new phases are formed by nucleating and growing[16-17]. With the increase of cooling rate, the increase of nucleation ratio[18], but the decrease of diffusion, the new phases are difficult to grow up[19-20]. Therefore, the smaller the modulus of specimens, the greater the cooling rate, and the less the thickness of laminar α+β phase formed in solid-state phase changes of Ti-6Al-4V alloy.

With increasing modulus, the increasing tendency of grain size and thickness of lamellar α+β phase decreases gradually. The increasing amplitude of grain size becomes slow with the modulus increasing. Consequently, the relationship between freezing thickness and time follows

                                   (4)

where  K is proportion factor, t is freezing time. Thus the freezing rate can be formulated by

                              (5)

Freezing acceleration is

＜0                    (6)

As shown in Eqns.(5) and (6), with time t increasing, the freezing velocity R and the amplitude of variation of freezing rate R both get smaller and smaller. From Eqn.(3), it can be concluded that although the modulus increment elongates the freezing time t, the increasing amplitude of grain size reduces with time.

For laminar α+β phase, the thickness of laminar α+β phase decreases with increase of cooling rate. And because the cooling rate is proportional to the freezing rate, the cooling rate and its amplitude of variation decrease gradually with the increase of freezing time. In similar manner, there is the same law in solid-state phase changes. Hence the increasing amplitude of lamellar α+β phase with modulus is smaller and smaller.

3.2 Relationship between microhardness and modulus, grain size, lamellar α+β phase thickness

The Vickers hardness of six specimens was measured systematically and respectively. Ten places were selected to carry out the microhardness test at every specimen, and then the average value was acted as the hardness value of this measured specimen. Thus the curve of the Vickers hardness(Hv) vs modulus(M) was obtained, as shown in Fig.7. It can be seen that the Vickers hardness decreases gradually and tends to be a constant with modulus increasing.

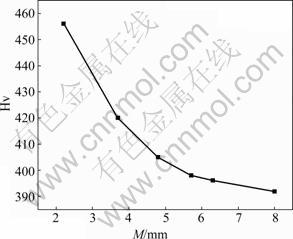
Fig.7 Relationship between Vickers hardness and casting modulus

Fig.8 and Fig.9 present the relation curves between Vickers hardness and  the thickness of laminar α+β phase d_α+β, respectively. It can be seen that the Vickers hardness decreases with grain size and d_α+β increasing. By fitting, the expression for relationship between Vickers hardness and grain size is written as

                      (7)

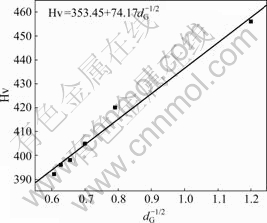
Fig.8 Relationship between microhardness and grain size

Fig.9 Relationship between microhardness and d_α+β

The above equation is in accordance with the form of Hall-Petch equation.

By means of the same fitting method, the fitted formula for relationship between the Vickers hardness and d_α+β was obtained: Hv=2.45-35.96d_α+β+476.74                (8)

Based on analysis in this paragraph, the smaller the casting modulus, the smaller the grain size and the thickness of laminar α+β phase, which enhances the effects of grain boundary intensity and phase boundary reinforcement. Moreover, the Vickers hardness is positively proportional to strength of alloy. Therefore, the Vickers hardness decreases with grain size and the thickness of laminar α+β phase increasing.

In the calculation of grain size and thickness of laminar α+β phase, when using the transversal method to measure the grain size, there is certain error due to the random-shaped grains of Ti-6Al-4V alloy. In addition, because of the crystal fixed phase of Ti-6Al-4V alloy, the selected milling faces in experience are not always perpendicular to the α+β phases. When the milling faces are at a certain angle to the α+β phases, the measured thickness of laminar α+β phases is larger than the real one. Only when they are perpendicular to each other, is the measured thickness of laminar α+β phases equal to the real one. This paper selects grains and α+β phases as many as possible to calculate their average value in order to reduce experimental error.

4 Conclusions

1) The grain size, d_G, and the thickness of laminar α+β phase, d_α+β, increase with casting modulus M. And the increasing tendency of grain size, d, and thickness of laminar α+β phase, d_α+β, decrease gradually with modulus M.

2) The Vickers hardness decreases with grain size and thickness of laminar α+β phase d_α+β increasing.

References

[1] AHMED T, FLOWER H M. Partial isothermal section of Ti-Al-V ternary diagram [J]. Materials Science and Technology, 1994, 10: 272.

[2] DIMIDUK D M, MIRACLE D B, WARD C H. Development of intermetallic materials for aerospace systems [J]. Materials Science and Technology, 1992, 8(3): 367-375.

[3] LEE D G, LEE Y H, LEE C SS, LEE S. Effects of volume fraction of tempered martensite on dynamic deformation properties of a Ti-6Al-4V alloy having a bimodal microstructure [J]. Metallurgical and Materials Transactions A, 2005, 36A: 741-748.

[4] LEE H, SHANKAR M, WILLIAM A. Fretting fatigue behavior of shot-peened Ti-6Al-4V under seawater environment [J]. Materials Science and Engineering A, 2006, 420(1/2): 72-78.

[5] KELLY S M, BABU S S, DAVID S A, ZACHARIA T, KAMPE S L. A thermal and microstructure model for laser deposition of Ti-6Al-4V [C]// Cost-Affordable Titanium, Dedicated to Professor Harvey Flower. Charoltte: Minerals, Metals and Materials Society, 2004: 45-52.

[6] SUZUKI K I, NISHIKAWA K, WATAKABE S. Mold filling and solidification during centrifugal precision casting of Ti-6Al-4V alloy [J]. Materials Transactions JIM, 1996, 37(12): 1793-1801.

[7] RAO Ping-gen, LWASA M, TAKAHIRO T, KONDOH I. Centrifugal casting of Al₂O₃-15ZrO₂ ceramic composites [J]. Ceramics International, 2003, 29(2): 209-212.

[8] WATANABE K, MIYAKAWA Q, TAKADA Y, OKUNO O, OKABE T. Casting behavior of titanium alloys in a centrifugal casting machine [J]. Biomaterials, 2003, 24(10): 1737-1743.

[9] HALVAEE E A, TALEBI A. Effect of process variables on microstructure and segregation in centrifugal casting of C92200 alloy [J]. Journal of Materials Processing Technology, 2001, 118(1/3): 123-127.

[10] MESQUITA R A, LEIVA D R, LEMOULEC A, YAVARI A R, BOTTA F W J. Rapidly solidified bulk Al alloys from a new centrifugal force casting [J]. Materials Science Forum, 2002, 403: 21-26.

[11] YEH Jien-wei. JONG Shang-haw, LIU Wen-pin. The improved microstructures and properties of 7075 alloys produced by a water-cooling centrifugal casting method [J]. Metallurgical and Materials Transactions A, 1996, 27(7): 1933-1944.

[12] YEH Jien-wei, JONG Shang-haw. The cast structure of a 7075 alloy produced by a water-cooling centrifugal casting method [J]. Metallurgical and Materials Transactions A, 1994, 25(3): 643-650.

[13] SEMIATIN S L, BIELER T R. Effect of texture changes on flow softening during hot working of Ti-6Al-4V [J]. Metallurgical and Materials Transactions A, 2001, 32A: 1871-1875.

[14] LEE D G, KIM S, LEE S, LEE C S, HUR S. Effects of microstructural morphology on quasi-static and dynamic deformation behaviors of Ti-6Al-4V alloy [J]. Metallurgical and Materials Transactions A, 2001, 34(2): 315-324.

[15] FLEMINGS M C, GUAN Yu-long, TU Bao-hong. Solidification process [M]. Beijing: Metallurgical Industry Press, 1987: 50-120. (in Chinese)

[16] ZHOU Yan-bang. Conspectus of titanium alloys casting [M]. Beijing: Aviating Industry Press, 2000: 83-86. (in Chinese)

[17] AHMED T, RACK H J. Phase transformations during cooling in alpha+beta titanium alloys [J].Mater Sci Eng, 1998, A243(1/2): 206-211.

[18] SUN Zhen-yan, LIU Chun-ming. Diffusion and phase transformation in alloys [M]. Shenyang: Northeastern University Press, 2002: 95-125. (in Chinese)

[19] JIN Yun-xue, ZENG Song-yan, WANG Hong-wei. Changes of carbides morphology in the alloy Ti15Al7C during heat treatment [J]. Rare Metal Materials and Engineering, 2002, 31(5): 358-362. (in Chinese)

[20] XU Zu-yao. Diffusion and growth in solid-state phase transformation [J]. Shanghai Metal, 1981, 2(4): 1-10. (in Chinese)

Foundation item: Project(50434030) supported by the National Natural Science Foundation of China

Corresponding author: SUI Yan-wei; Tel: +86-451-86412198; E-mail: suiyanwei@tom.com

(Edited by YANG Bing)