大直径气动潜孔锤动力学过程分析

訚耀保¹，黄帅¹，王康景¹，郭传新²

(1. 同济大学 机械与能源工程学院，上海，200092；

2. 北京建筑机械化研究院，北京，100007)

摘要：建立大直径气动潜孔锤的数学建模，通过动态过程数值模拟分析不同供气压力下气动潜孔锤结构参数对性能的影响。结果表明：过大的供气压力将使活塞超出设定行程，过小的供气压力无法形成较大的冲击频率。活塞低速时进气腔出现压力波动现象，这是由于进气量和容腔变化量相互作用引起的，可通过增大进气通道面积，减少压力波动。

关键词：大直径潜孔锤；数值仿真；压力波动；入岩；气动

中图分类号：TH47            文献标志码：A         文章编号：1672-7207(2014)03-0721-06

Analysis of kinetic process of large pneumatic down-the-hole hammer

YIN Yaobao¹, HUANG Shuai¹, WANG Kangjing¹, GUO Chuanxin²

(1. College of Mechanical Engineering, Tongji University, Shanghai 200092, China;

2. Beijing Institute of Construction Mechanization, Beijing 100007, China)

Abstract: The large pneumatic DTH (down-the-hole) hammer was designed. The working principle was analyzed and the mathematical model was built. With programming and numerical simulation of the dynamic process in MATLAB, the simulation results were compared under different input air pressures. The results show that the overlarge input pressure made the piston exceed the range and too low input pressure was unable to generate a proper impact frequency. The phenomenon of pressure oscillation happening in the inlet chamber during the process of dynamic simulation is caused by interaction of flowing gas and changing chamber. The pressure oscillation can be decreased by means of increasing the flow area.

Key words: large DTH hammer; programming simulation; pressure oscillation; entering-rock; pneumatics

在硬岩层及卵砾石土层上建设高层建筑、厂房、港口码头、公路、铁路、桥梁、水利水电枢纽等大型工程时，由于传统的桩锤无法实现入岩钻进，常采用大直径气动潜孔锤进行施工^[1-2]，钻进工艺为正循环钻进^[3]。目前国内使用的潜孔锤主要以直径300 mm以下的居多，直径 300 mm以上的钻孔属于大直径潜孔锤钻进范围^[4]，国内尚不多，大多依赖进口。大直径气动潜孔锤钻进过程的主要难点有：钻进直径大、钻孔地层复杂，钻孔垂直度施工要求高，灌注质量要好，孔位不能移动。这些特点及要求给大直径钻孔施工带来一定难度。通常情况下，大直径气动潜孔锤适用于上部为填土层或松散层，下部为中风化甚至新鲜基岩的地层^[5]；另一种情况是软层或松散层中夹大孤石、漂石，硬岩或大孤石钻进的工作量虽然在钻孔中只占总进尺的10%左右，但钻进效率很低，其钻进时间占总钻进时间的50%以上^[6]。大直径潜孔锤在工程应用中岩石坚硬致密，抗压强度大，孔径大，钻进效率低，常规低风压型空压机将无法配套使用；另外由于钻孔直径大，所需要大尺寸的潜孔锤冲击器，大尺寸设备在制造、装配的难度也直接影响该技术的推广应用。如何解决空压机匹配和结构优化这2个方面的要求，使其满足驱动冲击器碎岩功率的要求，这是研制大直径潜孔锤的关键^[7-9]。针对这些技术难点，本文作者采用新结构大直径气动潜孔锤并进行动力学分析，为其匹配合适的进气压力(空压机出口风压)，并分析和优化进气腔内的压力波动现象。

1  气动潜孔锤冲击器原理

1.1  所研制的潜孔锤的结构及原理

图1所示为所设计的大直径气动潜孔锤结构示意图。潜孔锤活塞采用二环面结构，构造较为简单，有利于降低制造成本。其工作原理如下：高压气体经过上接头1中心通孔，顶开逆止阀2进入潜孔锤内部。再依次经过配气座3上的轴向孔、内缸4与外缸5围成的通道、活塞6上的轴向槽，进入到前气室，后气室由活塞6中心通孔排气，活塞6在上下压力作用下往上加速，此过程为第1阶段；当活塞6上端面越过配气座3下端面时，后气室封闭压缩，前气室进气，活塞6向上加速，此过程为第2阶段；当活塞6运动至前气室的进气通道被堵后，前后气室都处于封闭状态，但前气室压力大于后气室压力，活塞仍向上加速，此过程为第3阶段；活塞6继续往上运动，将后气室的进气通道打开，气体进入到后气室，此时后气室压力超过前气室压力，活塞由向上加速运动变为向上减速运动，但速度未减为0 m/s，此过程为第4阶段；当活塞下端面越过排气阀7上端面时，下气室排气，上气室依然进气，活塞继续减速，直至速度减为0 m/s，此过程为第5阶段。以上5个阶段构成活塞6的回程运动，之后活塞6将向下做冲程运动，同样经历上述5个阶段，但顺序相反，最后活塞6撞击钻头9，产生冲击功；同时回转电机的动力经过上接头1、外缸5、下接头8传递给钻头9，实现钻头的回转运动。

由工作原理可知：潜孔锤单次循环可分为2个部分、10个阶段，其中回程部分分为：前气室进气、后气室排气阶段；前气室进气、后气室封闭阶段；前、后气室封闭阶段；前气室封闭、后气室进气阶段；前气室排气、后气室进气阶段。冲程部分分为：前气室排气、后气室进气阶段；前气室封闭、后气室进气阶段；前、后气室封闭阶段；前气室进气、后气室封闭阶段；前气室进气、后气室排气阶段。

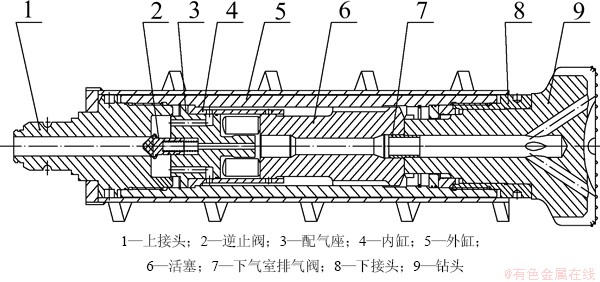
图1  气动潜孔锤结构示意图

Fig. 1  Structure diagram of pneumatic DTH hammer

1.2  气动潜孔锤数学模型

图2所示为潜孔锤的数学模型图。建模主要涉及热力学及动力学理论，具体包括：按照活塞运动微分方程, 求解活塞在此时间步长内的加速度、速度和位移以及前后气室的容积等参数。利用气体流动方程计算进入、排出前后气室气体质量；根据质量的变化，利用气体能量平衡方程计算前后气室内气体压力及温度的变化^[10-11]。

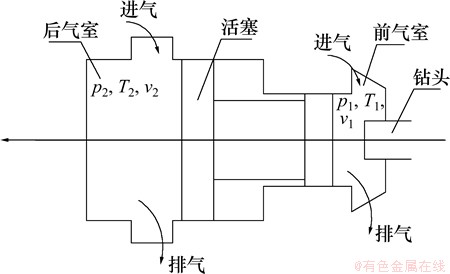
图2  气动潜孔锤数学模型图

Fig. 2  Mathematical model diagram of pneumatic DTH hammer

气体状态方程为：

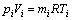                 (1)

式中：p_i为前后气室内气体的绝对压力；V_i为前后气室容积；m_i为前后气室内气体质量；R为摩尔气体常数；T_i为前后气室内气体的热力学温度。

活塞加速度微分方程为：

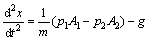           (2)

活塞速度微分方程为：

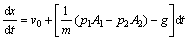        (3)

活塞位移微分方程为：

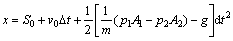    (4)

式中：x为活塞位移；m为活塞质量；p₁和p₂分别为前后气室内气体压力；A₁和A₂分别为前后气室活塞有效作用面积；v₀为活塞初速度；S₀为活塞初始位移；g为重力加速度。

气体流动方程为：

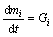                (5)

式中：m_i为前后气室气体质量；G_i为单位时间气体质量。

当计算流入或排出前后气室气体流量时，必须首先计算流经节流口处的风速，判断是属于何种音速，然后选择相应的计算公式。设气室的进排气过程为绝热膨胀过程，音速类别可由临界压力比ε判定：

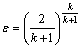              (6)

当p₂/p₁=ε时，气体流速等于音速；当1≥p₂/p₁≥ε时，气体流速小于第一速，即亚音速；当0≤p₂/p₁＜ε时，按超音速计算。

亚音速计算公式：

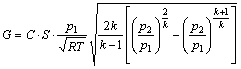    (7)

超音速计算公式：

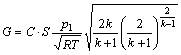        (8)

式中：k为绝热过程指数；S为进排气口截面积；p₁和p₂分别为气室内进、排气口处压力；η为气体流动阻力系数；T_i为前后气室内气体热力学温度。

考虑气体能量平衡方程，气室内气体压力变化量计算式：

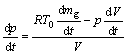            (9)

式中：dp为气室内压力变化量；V为前后气室容积；T₀为气源热力学温度；dm_g为气室内气体质量变化量；dV为气室体积变化量。

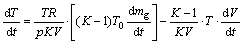    (10)

式中：dT为温度变化量。

2  结果分析

基于上述数学模型，利用有限差分原理，以matlab平台进行程序设计^[12-15]。数值计算过程中所用到的参数包括配气行程参数，气室通道面积，活塞质量、两端面积，前后气室的初始压力、体积、温度，活塞的初始位移、速度、加速度。针对所设计的600 mm钻孔直径的气动潜孔锤的活塞，大端直径为285 mm，小端直径为235 mm，质量为230 kg；潜孔锤冲击器的后气室排气长度为21 mm，前气室进气长度为28 mm，前气室进气+后气室封闭长度为58 mm，前气室进气+封闭长度为68 mm，活塞最大行程为170 mm；前气室进、排气通道面积分别4.55×10^-3和3.32×10^{-3 m2}，后气室进、排气通道面积分别为1.76×10^-3和5.02×10^{-3 m2}。在大直径钻孔过程中需要高风压以克服高抗压阻力，为本设计的潜孔锤匹配1.6 MPa出风压力的空压机^[16]，打开逆止阀损失0.2 MPa，忽略沿程阻力损失，则冲击器的入口压力为1.4 MPa，设定仿真步长为1 ms。

2.1  全工作过程结果分析

设定回程方向为正，冲程方向为负。图3所示为活塞的速度-位移关系曲线，活塞从静止向上做回程运动，最大速度为5.67 m/s，最大位移为164.1 mm；之后活塞开始做冲程运动，速度为负(向下)，当位移为0 mm时(即活塞撞击钻头时)，速度为7.07 m/s，整个过程所经历时间0.915 s，根据上述计算结果，可获得潜孔锤钻进频率和钻进功率等重要参数。图4所示为前后气室的压力-时间曲线。前气室在单循环中先后经历进气、封闭、排气，再到封闭、进气，压力p₁从进气压力1.4 MPa下降至大气压再上升至进气压力，后气室压力p₂则经历相反的过程。

2.2  不同进气压力下的潜孔锤性能参数对比

进气压力p₀是决定冲击功以及冲击频率的重要因素，因而也是影响钻速的主要参数，在复杂地层的大直径钻进中，应选择合适的供气压力以实现钻进效率。针对本文中所设计的大直径潜孔锤冲击器，初选与之匹配的冲击器进气压力为1.4 MPa，活塞的位移与速度随时间变化曲线如图5所示。

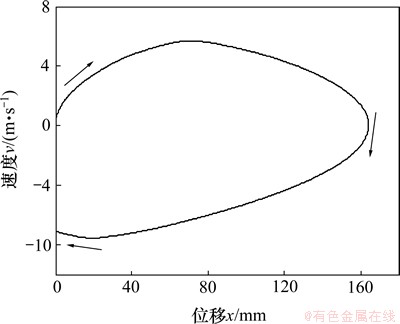
图3  活塞的速度-位移曲线

Fig. 3  Velocity-displacement curve of piston

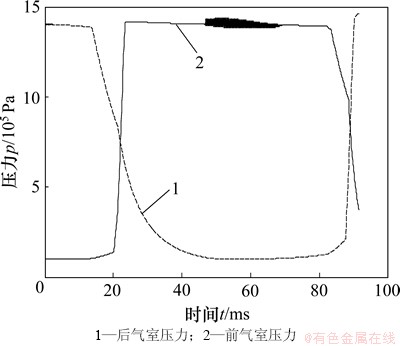
图4  前后气室压力-时间曲线

Fig. 4  Pressure-time curve of front and back air chamber

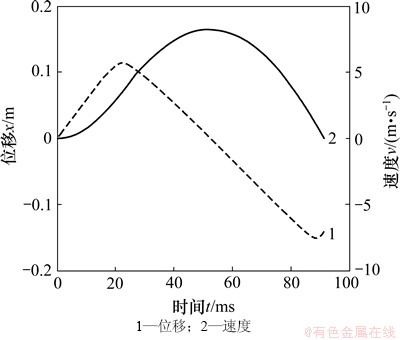
图5  进气压力1.4 MPa下活塞的位移与速度-时间曲线

Fig.5  Displacement and velocity-time curves of piston under inlet pressure of 1.4 MPa

在图5中，活塞在回程时(速度为正)，速度在第4阶段(前气室封闭、后气室进气)末达到最大，在第5段结束时回程位移达到最大，未超出行程范围(设计的最大行程为170 mm)，选择的进气压力符合要求。冲程时(速度为负)，活塞在第9阶段(前气室进气、后气室封闭阶段)末始时速度达到最大，之后速度开始下降，在第10阶段末撞击钻头。

为对所设计的大直径气动潜孔锤选择最合理的进气压力p₀，分别比较p₀为1.7，1.4，1.1和0.8 MPa时的潜孔锤冲击器性能。

图6所示为不同进气压力时的活塞速度曲线对比。由图6可见：当进气压力p₀为1.7 MPa时，活塞的运动曲线在回程运动的末尾处中断，这说明活塞的回程位移已经达到所设计的最大行程，活塞撞击了冲击器上端的配气座。其余3种进气压力下，潜孔锤具体的性能参数如表1所示(计算冲击功取活塞质量为230 kg)。在活塞回程位移不超过最大行程的条件下，进气压力越大活塞冲击功以及冲击频率都越大，钻进效果越好。

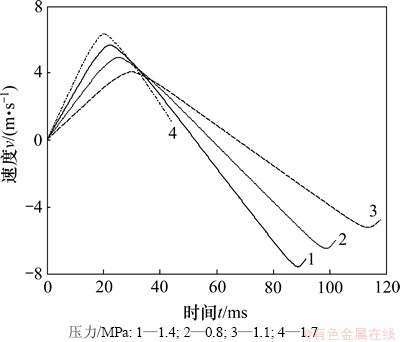
图6  不同进气压力时的活塞速度曲线对比

Fig. 6  Velocity-time curve comparison of 1.7, 1.4, 1.1 and 0.8 MPa inlet pressure

2.3  压力波动现象分析及参数优化

从冲击器的仿真结果可以看出，前后气室的压力在活塞处于低速时会出现波动现象，图7所示为回程运动起始时前气室的压力曲线。可见，压力在活塞开始运动时出现短暂的波动；图8所示为活塞运动至上止点附近，第5阶段结束第6阶段刚开始时的后气室压力，可以看出：此处的波动幅度更大，时间更长，占整个周期的1/4。

分析原因，由式(9)可见，气室内气体压力的变化率随气室的气体质量的变化量dm_g/dt增加而增加，随气室体积变化率dV/dt增加而减小。当活塞运动速度较低时，气室的体积变化率比较小，dV/dt对压力变化dp/dt的影响力与dm_g/dt相当，dp/dt在这2个因素的作用下时正时负，因此压力会出现波动，当活塞速度增大后dV/dt也增大，这时dV/dt对dp/dt起决定作用，进气室的压力沿一个方向变化，不会出现波动的现象。

表1  不同进气压力下潜孔锤冲击器的性能参数

Table 1  Performance parameters of hammer under different inlet pressures

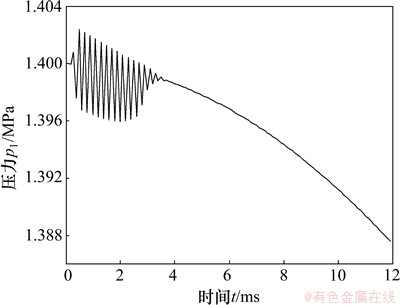
图7  回程刚开始阶段前气室压力-时间曲线

Fig. 7  Pressure-time curve of front air chamber at beginning of return stage

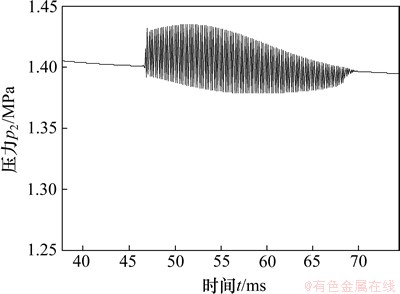
图8  回程结束冲程开始阶段后气室压力波动

Fig. 8  Pressure oscillation in back air chamber at end of return stage and beginning of stroke stage

前气室的压力波动持续时间极短且波动幅度小，可以忽略其影响，后气室压力波动持续时间长并波动幅值较大，会对潜孔锤的施工产生隐患。研究发现，增大后气室的进气通流面积可大幅度地减小此压力波动，图9所示为样机后气室的进气通道，它是4个开在冲击器内缸内壁上的槽，环向均匀分布。在加工槽时，增大槽的深度，将通流面积从原来的1.76×10^{-3 m2}增大到3.34×10^{-3 m2}，则增大了活塞低速时后气室的进气量，对后气室压力的稳定起到了作用。图10所示为增大通流面积后的回程结束冲程开始阶段后气室的压力，压力波动的振幅从原来的4×10⁴ Pa降为1.5× 10⁴ Pa，达到了比较好的优化效果。

图9  样机的内缸内表面上的后气室进气通道

Fig. 9  Inlet channel of back chamber on inner surface of inner casing of prototype

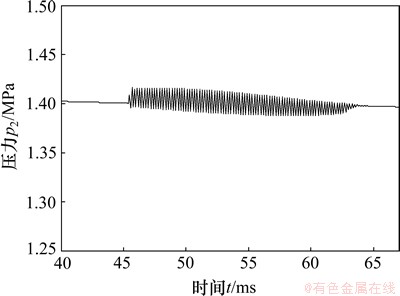
图10  增大通流面积后的后气室压力波动

Fig. 10  Pressure oscillation in back chamber after increasing flow area

3  结论

(1) 气动潜孔锤的动力学模型需要考虑热力学过程对气体状态的影响，可以通过数学建模和程序设计，进行大直径潜孔锤动态过程的数值模拟和关键结构参数设计。

(2) 对于所设计的大直径气动潜孔锤，过大的供气压力会使活塞运动超出最大行程，过小则无法产生钻进所需要的冲击功。在活塞不超出最大行程的条件下，选择的供气压力越大，钻进性能越好。

(3) 在活塞低速情况下进气气室会出现压力波动现象，特别是在行程末端这种波动持续时间较长，这种波动是低速情况下不可避免的现象，但通过增大气室通流面积的方法可大幅度的减小这种波动，这种方法在工艺上比较容易实现。本文分析结果对大直径气动潜孔锤设计理论和钻进技术拓展具有参考作用。

参考文献：

[1] 訚耀保, 梁之超, 黄帅, 等. 液压气动复合锤的快速下降过程分析[J]. 流体传动与控制, 2012, 51(2): 10-13.

YIN Yaobao, LIANG Zhichao, HUANG Shuai, et al. Analysis of fast dropping process of hydraulic-pneumatic hammer[J]. Fluid Power Transmission & Control, 2012, 51(2): 10-13.

[2] Chiang L E, Elias D A. Modeling impact in down-the-hole rock drilling[J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(4): 599-613.

[3] Lyons W C, GUO Bayum, Seidel F A. Air and gas drilling manual[M]. New York: The McGraw-Hill Companies, 2001: 232-233.

[4] 赵伟, 吴旭君, 郑平, 等. 大直径风动潜孔锤引孔技术在含漂石砾砂层预制桩施工中的应用与研究[J]. 广州建筑, 2009, 37(5): 70-72.

ZHAO Wei, WU Xujun, ZHENG Ping, et al. The application and research of the large diameter air operated down hole hammer in Guiding-hole for pile-sinking at the layer of gravel and boulders mixed together[J]. Guangzhou Architecture, 2009, 37(5): 70-72.

[5] Yue Z Q, Lee C F, Law K T, et al. Automatic monitoring of rotary-percussive drilling for ground characterization-illustrated by a case example in Hong Kong[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(4): 573-612.

[6] 杨国春, 尹洪峰, 傅丰均. 大直径硬岩钻进技术的探讨[J]. 长春工程学院学报(自然科学版), 2005, 6(3): 7-9.

YANG Guochun, YIN Hongfeng, FU Fengjun. Discussion of large diameter hard rock drilling technology[J]. Journal of Changchun Institute of Technology (Natural Sciences Edition), 2005, 6(3): 7-9.

[7] 郭传新. 中国桩工机械现状及发展趋势[J]. 建筑机械化, 2011, 32(8): 16-21.

GUO Chuanxin. The actuality and trend of China piling machinery[J].Construction Mechanization, 2011, 32(8): 16-21.

[8] Kahraman S, Bilgin N, Feridunoglu C. Dominant rock properties affecting the penetration rate of percussive drills[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(5): 711-723.

[9] Benamar A. Dynamic pile response using two pile-driving techniques[J]. Soil Dynamics and Earthquake Engineering, 2000, 20(4): 243-247.

[10] 徐小荷. 冲击凿岩的理论基础与电算方法[M]. 沈阳: 东北工学院出版社, 1986: 12-14.

XU Xiaohe. Theoretical basis and computing method of percussive drilling[M]. Shenyang: Northeast Institute of Technology Press, 1986: 12-14.

[11] 张国忠. 气动冲击设备及其设计[M]. 北京: 机械工业出版社, 1991: 102-110.

ZHANG Guozhong. Pneumatic impact equipment and its design[M]. Beijing: China Machine Press, 1991: 102-110.

[12] 熊青山, 殷琨. 气动潜孔锤仿真电算软件开发与应用[M]. 北京: 石油工业出版社, 2011: 8-54.

XIONG Qingshan, YIN Kun. The development and application of the computing software of pneumatic DTH hammer[M]. Beijing: Petroleum Industry Press, 2011: 8-54.

[13] QU Yegao, BU Changgen, LIU Baolin, et al. Numerical solution for dynamics of pneumatic DTH hammer system[J]. Exploration Engineering (Rock & Soil Drilling and Tunneling), 2009(S1): 170-176.

[14] 訚耀保. 高速气动控制理论和应用技术[M]. 上海: 上海科学技术出版社, 2014: 344-388.

YIN Yaobao. High speed pneumatic theory and technology[M]. Shanghai: Shanghai Scientific & Technical Publishers, 2014: 344-388.

[15] Chiang L E, Elia D A. A 3D FEM methodology for simulating the impact in rock-drilling hammers[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(5): 701-711.

[16] Kahraman S. Correlation of TBM and drilling machine performances with rock brittleness[J]. Engineering Geology, 2002, 65(4): 269-283.

(编辑  陈爱华)

收稿日期：2013-02-28；修回日期：2013-05-30

基金项目：国家科技支撑计划(“973”计划)项目(2011BAJ02B06)；国家自然科学基金资助项目(51175378，51275356)；航空科学基金资助项目(20120738001，20128038003)

通信作者：訚耀保(1965-)，男，湖北麻城人，博士，教授，博士生导师，从事极限环境下的流体传动与控制基础理论、飞行器能源与舵机和高速气动控制研究；电话：021-69589735；E-mail: y-yin@tongji.edu.cn