
ARTICLE
J. Cent. South Univ. (2019) 26: 1077-1088
DOI: https://doi.org/10.1007/s11771-019-4072-0
Three-dimensional analysis of natural convection in nanofluid-filled parallelogrammic enclosure opened from top and heated with square heater
Abdullah A.A.A AL-RASHED1, Walid HASSEN2, Lioua KOLSI2, 3,Hakan F. OZTOP4, 5, Ali J. CHAMKHA6, 7, Nidal ABU-HAMDEH5
1. Department of Automotive and Marine Engineering Technology, College of Technological Studies,
the Public Authority for Applied Education and Training, Kuwait;
2. Unité de Métrologie et des Systèmes  nergétiques,
nergétiques,  cole Nationale d’Ingénieurs, Monastir,University of Monastir, Tunisia;
cole Nationale d’Ingénieurs, Monastir,University of Monastir, Tunisia;
3. College of Engineering, Mechanical Engineering Department, Hail University, Hail City, Saudi Arabia;
4. Dept. Mech. Engineering, Technology Faculty, Firat University, TR-23119, Elazig, Turkey;
5. Department of Mechanical Engineering, King Abdulaziz University, Jeddah, Saudi Arabia;
6. Mechanical Engineering Department, Prince Sultan Endowment for Energy and Environment,
Prince Mohammad Bin Fahd University, Al-Khobar 31952, Saudi Arabia;
7. RAK Research and Innovation Center, American University of Ras Al Khaimah, P.O. Box 10021,Ras Al Khaimah, United Arab Emirates
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: A numerical study based on the finite volume method has been performed to study the three-dimension natural convection in a parallelogrammic top side opened cavity filled nanofluid with partially heated square at the bottom side. Results are obtained for different governing parameters such as nanoparticle concentration (f) from 0 to 0.05, inclination angle of the back and front walls (α) from 5° to 75°, Rayleigh number from 103 to 105, and length of heater changer from 0.1 to 1. The main finding from the obtained result showed that the inclination angle and nanoparticle volume fraction affect the flow structure and enhance the heat transfer.
Key words: 3D analysis; open enclosure; partial heating; parallelogram; nanofluids
Cite this article as: Abdullah A.A.A AL-RASHED, Walid HASSEN, Lioua KOLSI, Hakan F. OZTOP, Ali J. CHAMKHA, Nidal ABU-HAMDEH. Three-dimensional analysis of natural convection in nanofluid-filled parallelogrammic enclosure opened from top and heated with square heater [J]. Journal of Central South University, 2019, 26(5): 1077–1088. DOI: https://doi.org/10.1007/s11771-019-4072-0.
1 Introduction
Natural convection in open cavities can be encountered in several applications, such as mechanical engineering, thermofluid science, cooling of electronic components and cooling or heating of buildings. These applications have fully or partially heated as given in Ref. [1]. This situation can be applied to different shaped enclosures [2]. Nowadays, due to the technological advances all the electric and electronic components and devices tend to be more and more miniature. This size reduction represents a great challenge for engineers and researchers working on the development of the cooling techniques of these devices. One of the most innovative techniques is the use of nanofluids as cooling fluid.HUSSEIN et al [3] solved a problem to investigated convective heat transfer in open parallelepedic cavity filled with Cu nanoparticles dispersed in water. They showed that the inclination angle affects temperature filed. In another work of HUSSEIN [4], hemodeled the natural convection in a parallelogrammic cavity with hot concentric circular moving cylinder. He observed that Nusselt number decreases when the cylinder moves upward, while it increases when the cylinder moves downward. JAGADEESHA et al [5] studied the double diffusive natural convection in an inclined parallelogrammic porous closed space. They found that the inclination angle of the enclosure has significant influence on convective flow, heat and mass transfer characteristics. BAIRI [6] studied the natural convection in parallelogrammic enclosures in the presence of isothermal hot wall and he obtained correlations for different parameters for the studied geometry. COSTA et al [7] performed a work on double-diffusive natural convection in parallelogrammic closed spaces filled with moist air. He found that the high potential of the parallelogrammic enclosures most complete and even complex efficient heat and/or mass transfer systems. He found that geometrical parameters make the most important effect on heat and fluid flow. HAN et al [8] numerically studied the natural convection in a parallelogrammic shaped enclosure filled with a porous medium. Their results show that enhancement of heat transfer through the cavity is more pronounced as the inclination angle of the non-vertical sidewall increases. MAR A et al [9] proposed new correlations for natural convection in air-filled parallelogrammic cavities. They observed that heat transfer depends on inclination angle and Rayleigh number. VILLENEUVE et al [10] studied the thermal diode in a vertical stack for parallelogrammic closed spaces. Other interesting results related to the subject can be found in Ref. [11–21].
A et al [9] proposed new correlations for natural convection in air-filled parallelogrammic cavities. They observed that heat transfer depends on inclination angle and Rayleigh number. VILLENEUVE et al [10] studied the thermal diode in a vertical stack for parallelogrammic closed spaces. Other interesting results related to the subject can be found in Ref. [11–21].
The main aim of this computational study is to present the results of natural convection in a parallelogrammic open enclosure with a square heater filled with Al2O3-water nanofluid. Based on the above literature survey, there is no three-dimensional analysis in open literature for the studied geometry. Thus, the study will bring new results to literature to understand the heat and fluid flow characteristics.
2 Model definition
The computational model is defined in Figure 1. The cavity has a square heater on the bottom side and remaining part in bottom wall is considered adiabatic while top side is completely open. The cavity is parallelogrammic cavity with inclined front and back walls. Temperature of remaining walls is lower than that of heater.
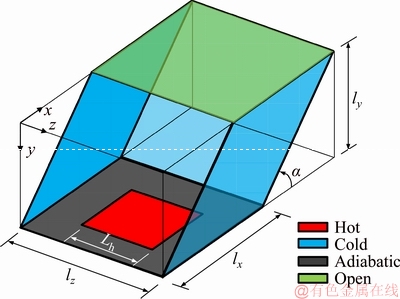
Figure 1 Studied configuration
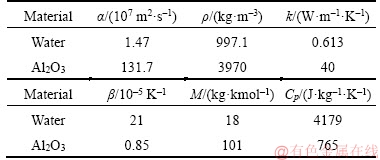
The nanofluid is considered incompressible and the flow is laminar. The thermo-physical properties of the base fluid and Al2O3 nanoparticles are presented in Table 1 (All properties are taken from Ref. [22] except the molar mass is taken from Ref. [23]).
Table 1 Properties of water and Al2O3 nanoparticle [22, 23]
3 Governing equations
Vorticity and vector potential are defined respectively by the following two expressions [24, 25]:
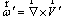 (1)
(1)
and
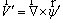 (2)
(2)
Using the dimensionless variables; equations governing the phenomenon are written as:
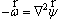 (3)
(3)
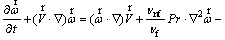
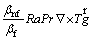 (4)
(4)
 (5)
(5)
with
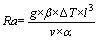 and
and 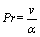 (6)
(6)
 (7)
(7)
The molecular weight, effective density and the specific heat and are expressed respectively as:
 (8)
(8)
 (9)
(9)
 (10)
(10)
The effective thermal conductivity is expressed as [23]:
 (11)
(11)
CHANDRASEKAR et al [23] determined experimentally the exponents a, b and c: a=–0.023, b=1.358 and c=0.126
FUSEGI et al [26] proposed an expression of the effective viscosity as follows:
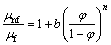 (12)
(12)
In the case of Al2O3/water nanofluid, the coefficients ‘‘b” and ‘‘n” were calculated experimentally by NONI et al [27] as 1631 and 2.8, respectively,The considered boundary conditions are:
Temperature:
T=1 for y=1 and
and
 (13)
(13)
 for y=1,
for y=1,  and
and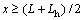
and  and
and 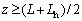 ) (14)
) (14)
 if n·V<0 and
if n·V<0 and  ,
,
if n·V≥0 at y=0 (open boundary) (15)
T=0 on all other walls (16)
Velocity:
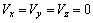 on all walls (17)
on all walls (17)
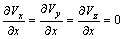 At open boundary (18)
At open boundary (18)
The local and average Nusselt numbers are defined as follows:
 (19)
(19)
 (20)
(20)
The blocked-off-region method [28] is used to follow the irregular shape of the geometry.
The grid dependency test is presented in Table 2 for α=30°, Ra=105, Lh=0.1 and f=0.05. The tests were conducted for spatial meshes of (81×61×71), (91×71×81), (101×81×91), and (110×91×101). The average Nusselt number was selected as a sensitive parameter. The incremental increase in the percentage of Nuav for grids of (91×71×81) to (101×81×91) is only 0.441%. Hence, considering the computational economy and accuracy, a spatial mesh size of (91×71×81) was chosen for the present study.
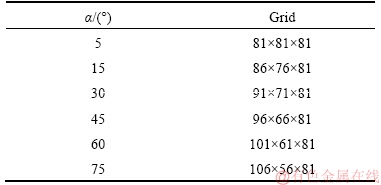
The grid is varied according to α as presented in Table 3.
The time step is fixed at 10-4 and the convergence criterion is:
Table 2 Grid sensitivity analysis for α=30°, Ra=105, Lh=0.1 and f=0.05
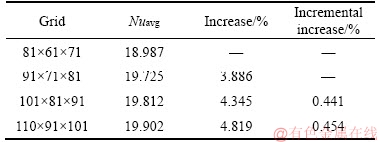
Table 3 Grid distributions
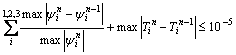 (21)
(21)
4 Code verification
A first code verification is performed by comparing with results of WAKASHIMA et al [29] and FUSEGI et al [26] as shown in Table 4. These authors studied the 3D natural convection of air-filled cavities. The agreement between results is excellent especially with those of WAKASHIMA et al [29] where the error percentage don’t exceed 2% except for Vxmax at Ra=105. The second verification is done for the case of nanofluid filled cavity by comparing with the studies of  ZTOP et al [30] (Figure 2) and of JAHANSHAHI et al [31] (Figure 3). Also a good agreement is observed.
ZTOP et al [30] (Figure 2) and of JAHANSHAHI et al [31] (Figure 3). Also a good agreement is observed.
5 Results and discussion
The effect of partially heated bottom wall of heat transfer and flow structure in an open sided parallelogrammic cavity filled with nanofluid is studied numerically.
Figure 4 illustrates the effect of heater width on flow structure for Ra=105 and α=45°. The more the heater area increases, the more the flow is intensified and the more complex the structure becomes. This is due to the increase of the contact area between the hot part and the fluid allowing intense variations of density that enhances the buoyancy forces. The intensity of the flow is more important near of the center of the heater. Due to the position of the heater in the center of the bottom wall, the fluid enters to the cavity from the left and right sides of the top opening (where the temperatures are lower) and leaves from the central part. For low heater widths, this behavior allows the creation of two vortexes due to friction between the laterally entering and central leaving fluids. For higher heater widths the vortex size reduces and the fluid mostly enters from the back region and leaves from the front one (nearest to the heater).
The flow structure is presented in Figure 5 in terms of particles trajectories for different inclination angles of front and back walls and fixed heater width (Lh=0.1) and fixed Rayleigh number (Ra=105). Due to the increase of inclination angle values the flow becomes pilled near the bottom wall. It is to be noted that the effect of adding nanoparticles is more important for low values of inclination angles. In fact in this case (α=15° and 30°) the increase of nanoparticles concentration causes the disappearance of the circulation vortexes and the fluid enters from the lateral regions and leaves directly from the central region without recirculation. This result is due to the heat intensification that augments the buoyancy forces allowing the fluid to leave the cavity before being cooled.
Figure 6 illustrates the temperature filed for Lh=0.1 and Ra=103 and 105 at different inclination angles (α), different nanoparticle volume fractions as φ=0 (gray) and φ=0.05 (colored). As clearly seen from the figure, a dome shaped temperature distribution is observed inside the cavity for all parameters. This shape turns to from sphere to ellipsoidal with increasing of Rayleigh number due to increasing of flow velocity. Addition of nanoparticle makes small effect on temperature distribution.
Table 4 Verification of code against results of WAKASHIMA et al [29] and FUSEGI et al [26]
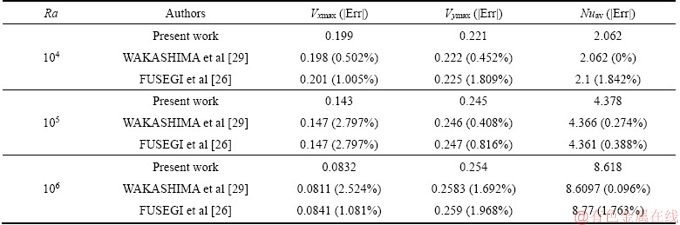
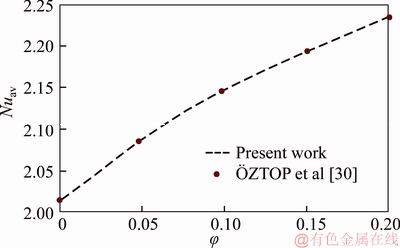
Figure 2 Comparison with results of  ZTOP et al [30] (Ra=104)
ZTOP et al [30] (Ra=104)
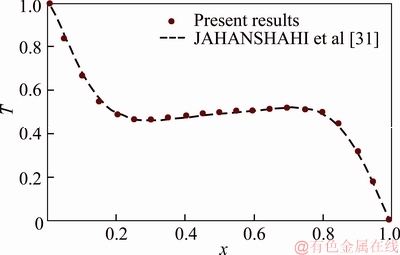
Figure 3 Comparison with results of JAHANSHAHI et al [31] (Pr=6.2, j=0.1 and Ra=6.2×104)
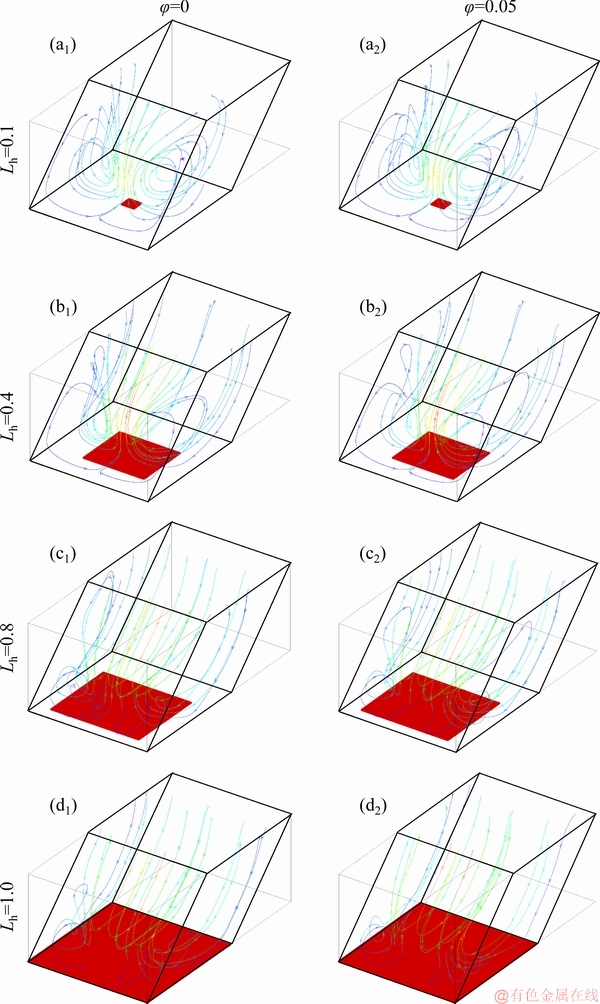
Figure 4 3D flow structure for Ra=105, α=45° for different Lh and j
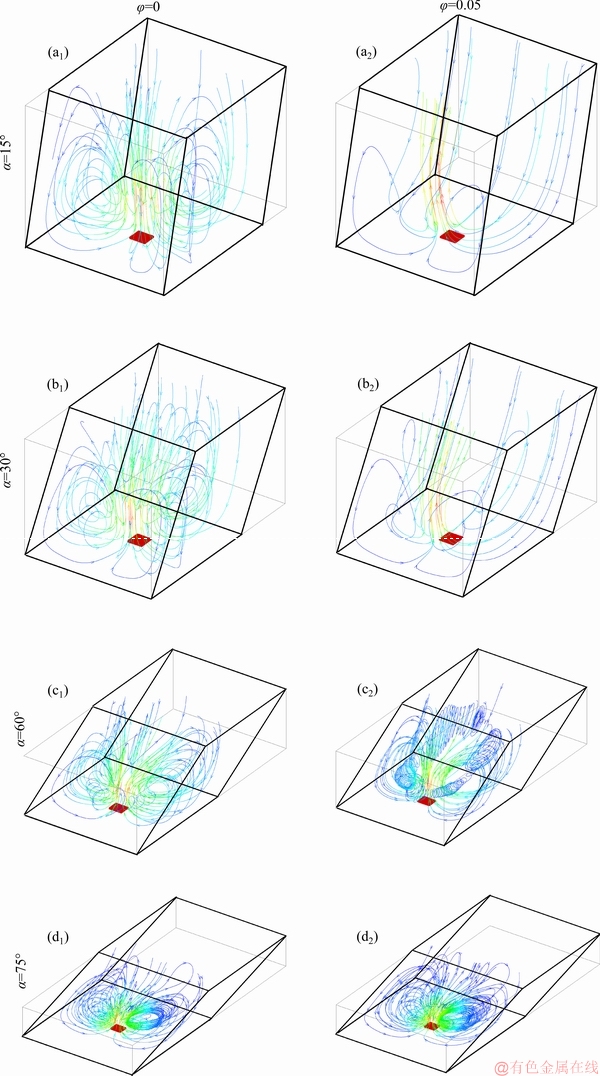
Figure 5 3D flow structure for Ra=105, Lh=0.1 and different α
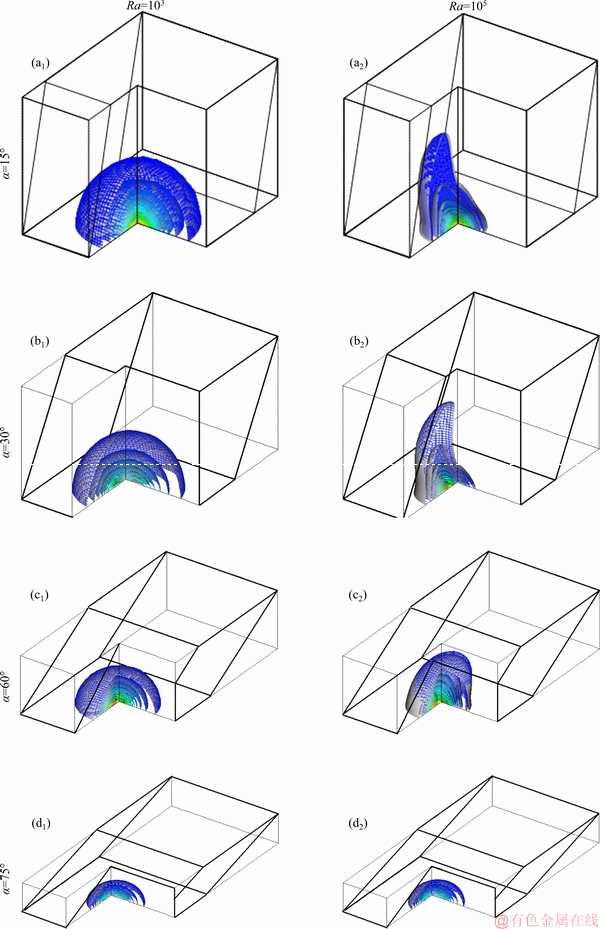
Figure 6 Temperature field for Lh=0.1, different Ra and α: φ=0 (Gray) and φ=0.05 (Colored)
Figure 7 also presents the results for Lh=0.8 with the same parameters of Figure 4. Thus, effects of heater length on temperature distribution can be seen clearly. As seen from the figure, the fluid tries to move up but the geometry is a border for it. Thus, the fluid moves to back side of the cavity. In the case of nanofluid, it goes further. This situation is clear in the case of a=30°. Also, the shape of core area changes with changing of inclination angle of the parallelogram.
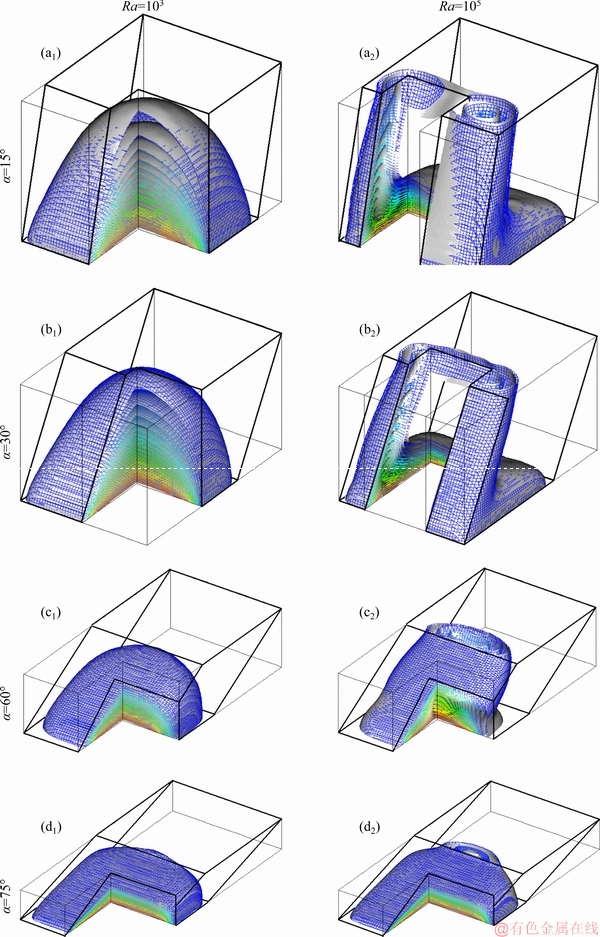
Figure 7 Temperature field for Lh=0.8, different Ra and α: φ=0 (Gray) and φ=0.05 (Colored)
Variation of average Nusselt number versus nanoparticle volume fraction for Ra=105 and Lh=0.1 is presented on Figure 8. It is seen that heat transfer is enhanced with increasing nanoparticle concentration. A more important enhancement of heat transfer occurs for the highest values of inclination and heater width.
Figures 9(a) and (b) illustrate the variation of average Nusselt number versus the inclination angle for different values of Lh and nanoparticle volume fraction for Ra=103 and Ra=105, respectively. Heat transfer is almost constant up to a=45o and it increases with increasing of inclination angle. There are little decreasing around a=65° for Ra=105 due to convection effects. In any case, higher heat transfer is formed for higher value of nanoparticle volume fraction for the same parameters. This variation is clearer from Figure 8.
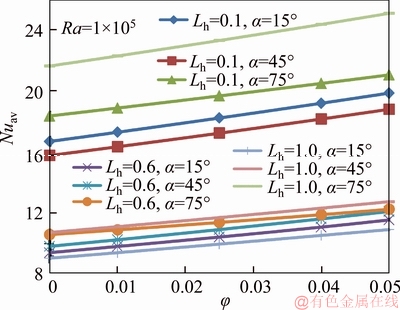
Figure 8 Nuav versus φ for Ra=105 and different Lh and α
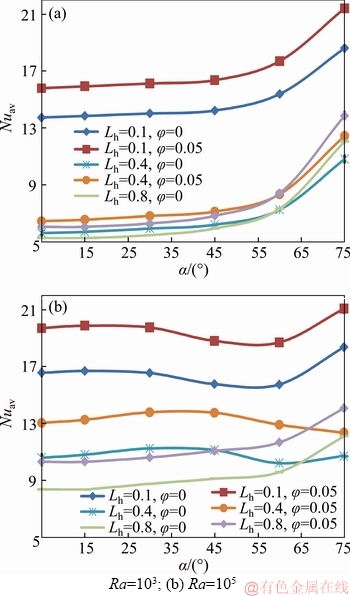
Figure 9 Nuav versus α for different Lh and φ:
Figure 10 presents the effects of Lh on heat transfer for different inclinations and nanoparticle concentrations: Ra=103 (Figure 8(a)) and Ra=105 (Figure 8(b)). As seen from the figure, there is a linear decreasing on heat transfer up to Lh=0.7 and 0.8 for all values of Ra number. This decrease is due to the recirculation vortexes that reduce the temperature gradients near the hot parts.
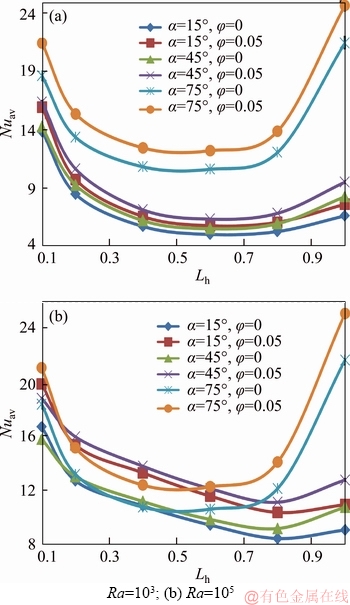
Figure 10 Nuav versus Lh for different α and φ:
Then, heat transfer increases especially for the higher values of Lh. This is due to the disappearance of the vortexes (Figure 4) allowing the entering of higher quantity of cold fluid.
Figure 11 presents the effect of Rayleigh number on Nusselt number for j=0.05 and different values of Lh and a. Heat transfer is almost constant for (Lh=0.1 and a=45°), (Lh=0.8 and a=75°) and (Lh=0.4 and a=75). Average Nusselt number decreases with increasing Lh and it increases with increasing Rayleigh number. For smaller values of Lh and inclination angle, heat transfer mode is almost conduction due to the reduced heat transfer domain.
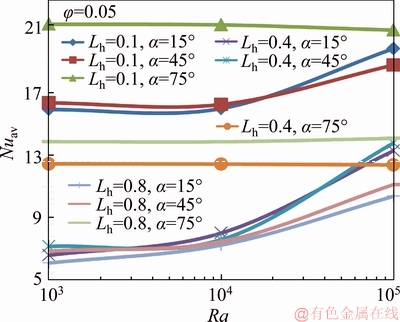
Figure 11 Nuav versus Ra for φ=0.05 and different Lh and α
6 Conclusions
The 3D natural convection in open sided parallelepedic cavity filled with nanofluid in the presence of partial square heater on the bottom wall is studied numerically. Governing equations are developed using the velocity vector-vorticty formalism and the finite volume. For all cases, heat transfer increases with increasing both nanoparticle volume fraction and inclination angle. For lower inclination angle it becomes almost constant for lower values of Rayleigh number. However, there is a decreasing around a=50o. Values of Nusselt number are depending on Lh values.
Nomenclature
Cp
Specific heat at constant pressure, J/(kg·K)
g
Gravitational acceleration, m/s2
k
Thermal conductivity, W/(m·K)
l
Enclosure width and height, m
Lh
Heater width
M
Molecular weight, kg/kmol
n
Unit vector normal to wall
Nu
Nusselt number
Pr
Prandtl number
Ra
Rayleigh number
t
Dimensionless time
T
Dimensionless temperature
Tc
Cold temperature, K
Th
Hot temperature, K
V
Dimensionless velocity vector
x, y, z
Dimensionless cartesian coordnates
Greek symbols
α
Thermal diffusivity, m2/s
β
Thermal expansion coefficient, K–1
ρ
Density, kg/m3
μ
Dynamic viscosity, kg/(m·s)
v
Kinematic viscosity, m2/s
j
Nanoparticles volume fraction
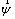
Dimensionless vector potential
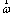
Dimensionless vorticity
ΔT
Dimensionless temperature
difference
Subscripts
av
Average
x, y, z
Cartesian coordinates
f
Fluid
nf
Nanofluid
s
Solid
References
[1] YUNCU H, YAMAC S. Laminar natural convective heat transfer in an air-filled parallelogramic cavity [J]. International Communication in Heat and Mass Transfer, 1991, 18: 559–568. DOI: 10.1016/0735-1933(91)90069-G.
[2] ALDRIDGE K D, YAO H. Flow features of natural convection in a parallelogrammic enclosure [J]. International Communication in Heat and Mass Transfer, 2001, 28: 923–931. DOI: 10.1016/S0735-1933(01)00296-2.
[3] HUSSEIN A K, MUSTAFA A W. Natural convection in fully open parallelogrammic cavity filled with Cu-water nanofluid and heated locally from its bottom wall [J]. Thermal Science and Engineering Progress, 2017, 1: 66–77. DOI: 10.1016/ j.tsep.2017.03.002.
[4] HUSSEIN A K. Computational analysis of natural convection in a parallelogrammic cavity with a hot concentric circular cylinder moving at different vertical locations [J]. International Communications in Heat and Mass Transfer, 2013, 46: 126–133. DOI: 10.1016/ j.icheatmasstransfer.2013.05.008.
[5] JAGADEESHA R D, PRASANNA B M R, SANKAR M. Double diffusive convection in an inclined parallelogrammic porous enclosure [J]. Procedia Engineering, 2015, 127: 1346–1353. DOI: 10.1016/j.proeng.2015.11.493.
[6] BAIRI A. On the Nusselt number definition adapted to natural convection in parallelogrammic cavities [J]. Applied Thermal Engineering, 2008, 28: 1267–1271. DOI: 10.1016/ j.applthermaleng.2007.10.025.
[7] COSTA V A F, OLIVEIRA M S A, SOUSA A C M. Laminar natural convection in a vertical stack of parallelogrammic partial enclosures with variable geometry [J]. International Journal of Heat and Mass Transfer, 2005, 48: 779–792. DOI: 10.1016/j.ijheatmasstransfer.2004.09.012.
[8] HAN H S, HYUN J M. Buoyant convection in a parallelogrammic enclosure filled with a porous medium– General analysis and numerical simulations [J]. International Journal of Heat and Mass Transfer, 2008, 51: 2980–2989. DOI: 10.1016/j.ijheatmasstransfer.2007.09.015.
[9] de MAR A G J M, BA
A G J M, BA RI A, COSTA V A F. Empirical correlations at high Ra for steady-state free convection in 2D air-filled parallelogrammic enclosures with isothermal discrete heat sources [J]. International Journal of Heat and Mass Transfer, 2010, 53: 3831–3838. DOI: 10.1016/j.ijheatmasstransfer.2010.04.036.
RI A, COSTA V A F. Empirical correlations at high Ra for steady-state free convection in 2D air-filled parallelogrammic enclosures with isothermal discrete heat sources [J]. International Journal of Heat and Mass Transfer, 2010, 53: 3831–3838. DOI: 10.1016/j.ijheatmasstransfer.2010.04.036.
[10] VILLENEUVE T, BOUDREAU M, DUMAS G. The thermal diode and insulating potentials of a vertical stack of parallelogrammic air-filled enclosures [J]. International Journal of Heat and Mass Transfer, 2017, 108: 2060–2071. DOI: 10.1016/j.ijheatmasstransfer.2016.12.067.
[11] MAHMOODI M, KANDELOUSI S. Kerosene-alumina nanofluid flow and heat transfer for cooling application [J]. Journal of Central South University, 2016, 23(4): 983–990. DOI: 10.1007/s11771-016-3146-5.
[12] SARI M R, KEZZAR M, ADJABI R. Heat transfer of copper/water nanofluid flow through converging-diverging channel [J]. Journal of Central South University, 2016, 23(2): 484–496. DOI: 10.1007/s11771-016-3094-0.
[13] MAJID S, MOHAMMAD J. Optimal selection of annulus radius ratio to enhance heat transfer with minimum entropy generation in developing laminar forced convection of water-Al2O3 nanofluid flow [J]. Journal of Central South University, 2017, 24(8): 1850–1865. DOI: 10.1007/s11771- 017- 3593-7.
[14] WUSIMAN K, CHUNG H, NINEMD J, HANDRY A, EOM Y, KIM J, JEONG H. Heat transfer characteristics of nanofluid through circular tube [J]. Journal of Central South University, 2013, 20(1): 142–148. DOI: 10.1007/s11771- 013-1469-z.
[15] MOHEBBI R, LAKZAYI H, SIDIK N A C, JAPAR W M A A. Lattice boltzmann method based study of the heat transfer augmentation associated with Cu/water nanofluid in a channel with surface mounted blocks [J]. International Journal of Heat and Mass Transfer, 2018, 117: 425–435. DOI: 10.1016/j.ijheatmasstransfer.2017.10.043.
[16] MOHEBBI R, IZADI M, CHAMKHA A J. Heat source location and natural convection in a C-shaped enclosure saturated by a nanofluid [J]. Physics of Fluids, 2017, 29: 122009. DOI: 10.1063/1.4993866.
[17] IZADI M, HOGHOUGHI G, MOHEBBI R, SHEREMET M. Nanoparticle migration and natural convection heat transfer of Cu-water nanofluid inside a porous undulant-wall enclosure using LTNE and two-phase model [J]. Journal of Molecular Liquids, 2018, 261: 357–372. DOI: 10.1016/ j.molliq.2018.04.063.
[18] KASAEIPOOR A, MALEKSHAH E H, KOLSI L. Free convection heat transfer and entropy generation analysis of MWCNT-MgO (15%–85%)/water nanofluid using lattice Boltzmann method in cavity with refrigerant solid body— Experimental thermo-physical properties [J]. Powder Technology, 2017, 322: 9–23. DOI: 10.1016/j.powtec. 2017.08.061.
[19] EMAMI R Y, SIAVASHI M, MOGHADDAM G S. The effect of inclination angle and hot wall configuration on Cu-water nanofluid natural convection inside a porous square cavity [J]. Advanced Powder Technology, 2018, 29(3): 519–536. DOI: 10.1016/j.apt.2017.10.027.
[20] TOOSI M H, SIAVASHI M. Two-phase mixture numerical simulation of natural convection of nanofluid flow in a cavity partially filled with porous media to enhance heat transfer [J]. Journal of Molecular Liquids, 2017, 238: 553–569. DOI: 10.1016/j.molliq.2017.05.015.
[21] GHASEMI K, SIAVASHI M. Lattice Boltzmann numerical simulation and entropy generation analysis of natural convection of nanofluid in a porous cavity with different linear temperature distributions on side walls [J]. Journal of Molecular Liquids, 2017, 233: 415–430. DOI: 10.1016/ j.molliq.2017.03.016.
[22] KOLSI L, KALIDASAN K, ALGHAMDI A, BORJINI M N, KANNA P R. Natural convection and entropy generation on a cubical cavity with twin adiabatic blocks and filled by aluminium oxide-water nanofluid [J]. Numerical Heat Transfer Part A, 2016, 70(3): 242–259. DOI: 10.1080/ 10407782.2016.1173478.
[23] CHANDRASEKAR M, SURESH S, CHANDRA BOSE A. Experimental investigations and theoretical determination of thermal conductivity and viscosity of Al2O3/water nanofluid [J]. Experimental Thermal and Fluid Science, 2010, 34: 210–216. DOI: 10.1016/j.expthermflusci.2009.10.022.
[24] ABIDI A, KOLSI L, BORJINI M N, BEN A SSIA H. Effect of radiative heat transfer on three-dimensional double diffusive natural convection [J]. Numerical Heat Transfer Part A, 2011, 60(9): 785–809. DOI: 10.1080/10407782. 2011.627797.
SSIA H. Effect of radiative heat transfer on three-dimensional double diffusive natural convection [J]. Numerical Heat Transfer Part A, 2011, 60(9): 785–809. DOI: 10.1080/10407782. 2011.627797.
[25] KOLSI L, ABIDI A, BORJINI M N, BEN A SSIA H. The effect of an external magnetic field on the entropy generation in three-dimensional natural convection [J]. Thermal Science, 2010, 14(2): 341–352. DOI: 10.1080/10407790601184462.
SSIA H. The effect of an external magnetic field on the entropy generation in three-dimensional natural convection [J]. Thermal Science, 2010, 14(2): 341–352. DOI: 10.1080/10407790601184462.
[26] FUSEGI T, HYUN J M, KUWAHARA K, FAROUK B. A numerical study of three-dimensional natural convection in a differentially heated cubical enclosure [J]. International Journal of Heat and Mass Transfer, 1991, 34: 1543–1557. DOI: 10.1016/0017-9310(91)90295-P.
[27] NONI A D, GARCIA D E, HOTZA D. A modified model for the viscosity of ceramic suspensions [J]. Ceramics International, 2002, 28: 731–735. DOI: 10.1016/S0272- 8842(02)00035-4.
[28] PATANKAR S V. Numerical heat transfer and fluid flow [M]. Philadelphia, USA: Taylor & Francis, 1981.
[29] WAKASHIMA S, SAITOH T S. Benchmark solutions for natural convection in a cubic cavity using the high-order time–space method [J]. International Journal of Heat and Mass Transfer, 2004, 47: 853–864. DOI: 10.1016/ j.ijheatmasstransfer.2003.08.008.
[30]  ZTOP H F, ABU-NADA E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids [J]. International Journal of Heat and Fluid Flow, 2008, 29(5): 1326–1336. DOI: 10.1016/ j.ijheatfluidflow.2008.04.009.
ZTOP H F, ABU-NADA E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids [J]. International Journal of Heat and Fluid Flow, 2008, 29(5): 1326–1336. DOI: 10.1016/ j.ijheatfluidflow.2008.04.009.
[31] JAHANSHAHI M, HOSSEINIZADEH S F, ALIPANAH M, DEHGHANI A, VAKILINEJAD G R. Numerical simulation of free convection based on experimental measured conductivity in a square cavity using water/SiO2 nanofluid [J]. International Communications in Heat and Mass Transfer, 2010, 37: 687–694. DOI: 10.1016/j.icheatmasstransfer. 2010.03.010.
(Edited by YANG Hua)
中文导读
纳米流体在顶部开孔底部加热的四方形容器内的三维自然对流
摘要:构建纳米流体在顶部开孔底部加热的四方形容器流动模型,基于有限体积法,进行了纳米流体三维自然对流的数值研究。得到的控制参数为纳米粒子浓度(φ)0~0.05、前后壁倾角(α)5°~75°、Rayleigh数103~105、加热器的换热器长度0.1~1。结果表明,倾角和纳米颗粒的体积分数影响流动结构,提高了传热效果。
关键`词:三维分析;开放式外壳;部分加热;平行四边形;纳米流体
Received date: 2018-08-09; Accepted date: 2018-09-30
Corresponding author: Lioua KOLSI, PhD, Associate Professor; E-mail: lioua_enim@yahoo.fr; ORCID: 0000-0003-4368-7458