J. Cent. South Univ. Technol. (2010) 17: 1119-1124

DOI: 10.1007/s11771-010-0605-2

Effect of heterogeneity on mechanical and acoustic emission characteristics of rock specimen

LI Shu-cai(李术才), LI Guo-ying(李国莹)

Geotechnical and Structural Engineering Research Center, Shandong University, Jinan 250061, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2010

Abstract: The influence of heterogeneity on mechanical and acoustic emission characteristics of rock specimen under uniaxial compress was studied with numerical simulation methods. Weibull distribution function was adopted to describe the mesoscopic heterogeneity of rocks. The failure process of heterogeneous rock specimen under uniaxial loading was simulated using FLAC^3D software. Five schemes were adopted to investigate the influence of heterogeneity. The results demonstrate that as the homogeneity increases, the peak strength and brittleness of rocks increase, and the macro elastic modulus improves as well. Heterogeneity has great influence on macro elastic modulus and strength when the homogeneity coefficient is less than 20.0. The volume expansion is not so obvious when the homogeneity increases. As the homogeneity coefficient increases the acoustic emissions modes change from swarm shock to main shock. When the homogeneity coefficient is high, the cumulative acoustic emission events-axial strain curve is gentle before the rock failure. The numerical results agree with the previously numerical results and earlier experimental measurements.

Key words: heterogeneity; acoustic emission; strain softening; numerical simulation; uniaxial compression; elastic modulus

1 Introduction

In general, studies on mechanical properties and failure process of rocks are based on the assumption that rocks are homogeneous materials. However, rocks are heterogeneous materials on the mesoscopic scale. Their spatial distributions of physical and mechanical properties are discontinuous. Heterogeneity has great effect on the mechanical and deformational properties as well as acoustic emission characteristics of rocks.

Weibull described the heterogeneity of materials with probability and statistics method. Weibull statistical distribution was widely used to reflect the heterogeneity of rock materials. YOU and ZOU [1] discussed the heterogeneity of rock materials and the size effect on specimen strength. In recent years, with the development of computer technology, more and more researchers have used numerical methods to study the heterogeneous materials [2-8]. The numerical methods included the finite element method [9-10], the finite difference method [11-12] and the discrete element method. The common software used to simulate the rock failure process contained RFPA (rock failure process analysis) [13-14], R-T^2D (rock and tool interaction) [15-16], and EPCA (elasto-plastic cellular automaton) [17-18]. FLAC^3D was a finite difference method and widely used in the numerical simulation in geotechnical engineering. But, the study on the property and failure process of heterogeneous rocks with FLAC^3D was limited.

During the rock failure process, the acoustic emission phenomenon was obvious. Acoustic emission modes were not the same for different heterogeneous rocks. MOGI [19] pointed out three acoustic emission (AE) modes of materials. Based on the theory of damage mechanics and the principle of rock acoustic emission, TANG [20] put forward the assumption that rock acoustic emission was consistent with rock damage. LIANG et al [21] studied the basic modes of rock acoustic emission with simulation method.

In this work, FLAC^3D software was used to analyze the effect of heterogeneity on mechanical and deformational characteristics of rock specimens. Through compiling FISH functions, the AE events during the failure process of rocks were recorded, and the characteristics of acoustic emission in the uniaxial test of rock specimens with different homogeneous degrees were studied.

2 Constitutive relation and model

The strain-softening constitutive model was used in this simulation. The failure criterion used was a composite Mohr-Coulomb criterion with tension cut-off. This constitutive model was based on the Mohr-Coulomb model with non-associated shear and associated tension flow rules [11, 22]. The Mohr-Coulomb failure criterion had the form of  with

                     (1)

The tension failure criterion had the form of  with

                                 (2)

where φ is the friction angle; c is the cohesion; and is the tensile strength.

The distinctive of the constitutive model was that the constitutive relation was linearly elastic before the plastic yield, while after the plastic yield the cohesion and friction were defined as piecewise-linear functions of the plastic strain [11, 22].

The rock specimen was 50 mm in thickness, 50 mm in width and 100 mm in height. It was divided into    16 000 (20×20×40) elements and the element size was 2.5 mm. The model was loaded at a constant velocity of 5×10^{-9 m/time step at} the two ends of the specimen. The material properties used in the simulation are given in Table 1. The functions of the mobilized cohesion and friction angle can be established by considering laboratory test data, the GSI (geological strength index) system as well as back analysis of field measurements [23-24]. In this work, the piecewise-linear functions were used. The variation of cohesion and friction angle with plastic strain is shown in Table 2.

Table 1 Material properties of rocks used in simulation

Table 2 Variations of cohesion (c) and friction angle with plastic strain

Weibull distribution function was adopted to study the mesoscopic heterogeneity of rocks. The function was expressed as:

           (3)

where  is the elemental parameter;  is the mean value of the elemental parameter; and M is the homogeneity coefficient, which describes the homogeneous degree of mesoscopic mechanical properties. Using FISH language to compile the program, the mechanical properties of the elements were randomly assigned in the mode. Five schemes for calculations were adopted in this work. From schemes 1 to 4, the homogeneity coefficients were 1.1, 2.0, 5.0 and 10.0, respectively, as illustrated in Figs.1-2. In this work, only the effect of elastic modulus heterogeneities on mechanical and deformational characteristics of rock specimen was considered, others mechanical properties of the elements such as cohesion and friction angle were still homogeneous.

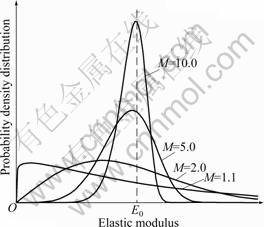
Fig.1 Distribution of elastic modulus for different heterogeneous rocks

Fig.2 Distribution of elastic modulus for typical heterogeneous rock (M=2.0)

3 Results and analysis

3.1 Effect of heterogeneity on axial stress-strain curve

The axial stress-strain curves and the AE events-strain (AE events represent the number of the elements) curves of rocks in the uniaxial test with different heterogeneous degrees are illustrated in Figs.3-4. The numerical results indicate that the peak strength and strain are improved with the increase of the

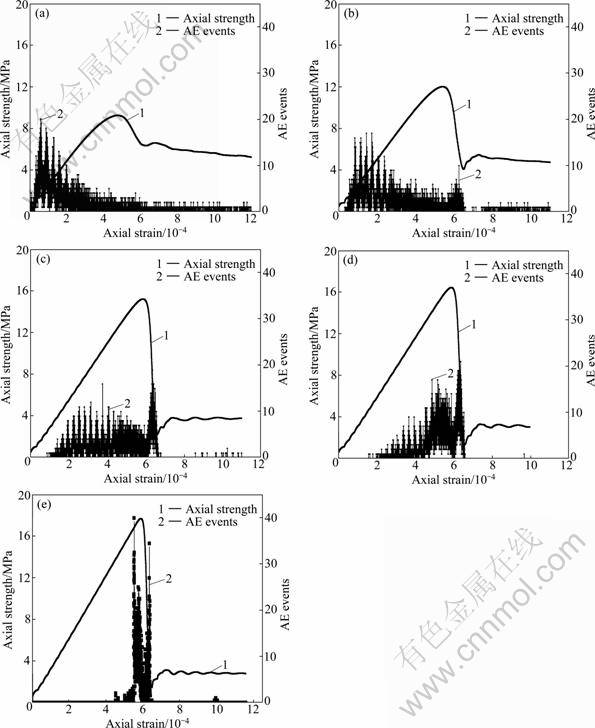
Fig.3 Axial stress-strain curves and AE events- strain curves for different heterogeneous rocks: (a) M=1.1; (b) M=2.0; (c) M=5.0; (d) M=10.0;  (e) Homogeneous rock

homogeneity. The homogeneity coefficient describes the homogeneous degree of mesoscopic mechanical properties of rock materials. As the homogeneity coefficient decreases, the discreteness of the material parameter improves. Some elements fail under low  stress, which decreases the macro strength of rock specimen, and rocks experience ductile failure.

As the homogeneity coefficient increases, the mechanical parameters of elements are more concentrated. The numbers of the elements with low mechanical parameters reduce. Fewer elements fail before the peak strength, and the stress transfer and crack extension are inadequate. Rocks experience brittle  failure. These numerical results coincide with the experimental and simulated results in Refs.[13-14].

Fluctuation exists in the residual phase of the stress-strain curves. This phenomenon can be also seen in Ref.[22]. The inertial effect introduced by the rate of loading is one of the reasons, which does not affect the reliability of the model and the analysis in this work.

Fig.4 Axial stress-strain curves for different heterogeneous rocks

3.2 Effect of heterogeneity on macro elastic modulus and strength

In order to analyze the relationship among macro elastic modulus, strength and the homogeneity coefficient, the rock specimens with homogeneity coefficients of 20.0, 50.0, and 100.0 were added in the simulation. The curves among the macro elastic  modulus, peak strength and the homogeneity coefficient were drawn. Nonlinear fitting method was adopted to deal with the simulated results. The fitting functions were obtained. As shown in Figs.5-6, the macro peak strength and the macro elastic modulus are enhanced when the homogeneity coefficient of rock materials improves. These conclusions agree with the experimental and simulated results in Refs.[13-14].

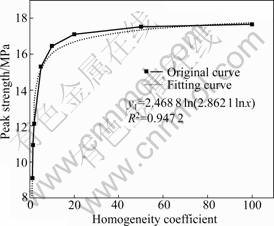
Fig.5 Relationship between macro peak strength and heterogeneity coefficient

The fitting function between peak strength and the homogeneity coefficient is

                     (4)

The fitting function between macro elastic modulus and the homogeneity coefficient is

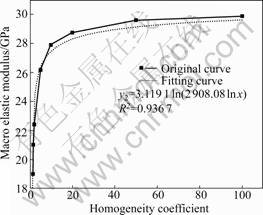
Fig.6 Relationship between macro elastic modulus and heterogeneity coefficient

                    (5)

where x is the homogeneity coefficient; y₁ is the peak strength; and y₂ is the macro elastic modulus.

The results show that the heterogeneity has great influence on macro elastic modulus and strength when the homogeneity coefficient is less than 20.0. However, when the homogeneity coefficient is more than 50.0, it has much less influence on macro elastic modulus and strength, and the macro elastic modulus tends to be the mean elastic modulus. These conclusions agree with the simulated results in Ref.[14].

3.3 Effect of heterogeneity on AE modes

Based on the assumption of TANG [20] that rock AE was consistent with rock damage, through compiling FISH functions the AE events during the failure process of rocks were recorded. The rock AE was proportional to rock damage. The law of AE can be obtained. The effects of heterogeneity on the AE events as well as the cumulative AE events in the uniaxial test were studied.

The cumulative AE events-strain curves for different homogeneity coefficients are shown in Fig.7. In

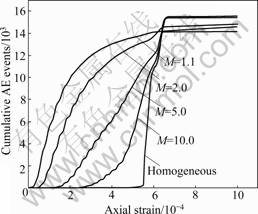
Fig.7 Cumulative AE events-axial strain curves for different heterogeneous rocks

the loading process, AE events are obvious. As the elastic moduli of the elements are different, the elements with low failure strength fail earlier than those with high failure strength. Heterogeneity degree has great effect on the AE modes [14, 21]. Through analyzing the AE modes of rock failure process and finding the AE discipline before rock failure, new methods and foundation can be found to forecast the failure of rocks.

Study shows that when the homogeneity coefficient is low, and many elements fail before and after the peak strength, the AE mode is swarm shock. As the homogeneity coefficient increases, the corresponding strain of the peak AE events improves, and the AE mode changes to pre-main-after shocks. For homogeneous rock specimens, the AE events concentrate in peak strength. The AE events are very few before and after the peak strength. The AE mode is the main shock, and the rock experiences brittle failure. From Fig.7, it is found that the cumulative AE events after the failure of rock are nearly the same.

3.4 Effect of heterogeneity on deformation chara- cteristics of rock specimens

From Fig.8 it is found that the volumetric strain changes from positive to negative, which reflects that the volume of rock specimen first decreases and then increases during the uniaxial test. At last, the volume of rock specimen is greater than the initial size, and rock shows the characteristics of shear dilatancy.

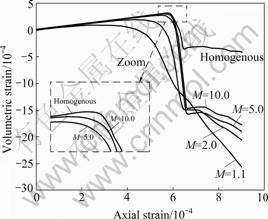
Fig.8 Volumetric strain-axial strain curves for different heterogeneous rocks

The peak volumetric strain improves when the homogeneity coefficient increases. This indicates that the volume compression ratio of homogeneous rock is the largest during the uniaxial test. As the homogeneity coefficient decreases the absolute value of the ultimate volumetric strain improves. This reflects that the more heterogeneous the rock specimen the bigger the volume expansion during the uniaxial test. That is because as the homogeneity coefficient decreases, the number of the elements with low elastic modulus increases. So, the ability to resist deformation reduces and the rock specimen yields large deformation.

Before the rock failure, the volumetric strain-axial strain curves undergo nonlinear changes. The nonlinear changes are more obvious when the homogeneity coefficient decreases. The curves have a mutation when the rock specimens reach the peak strength.

4 Conclusions

(1) The macro elastic modulus and strength increase when the homogeneity coefficient of rock material improves. The fitting functions among macro strength, macro elastic modulus and the homogeneity coefficient are given. Heterogeneity has great influence on macro elastic modulus and strength when the homogeneity coefficient is less than 20.

(2) Before the rock failure, the volumetric strain-axial strain curves undergo nonlinear changes. The nonlinear changes and volume expansion are more obvious when the homogeneity coefficient decreases.

(3) The characteristics of AE for rock specimen under uniaxial loading are studied. When the homogeneity coefficient is low the AE precursors to rock failure are apparent. As the homogeneity coefficient increases the acoustic emission modes change from swarm shock to main shock.

(4) When the homogeneity coefficient is high, the cumulative AE events-axial strain curve is gentle before the rock failure, because there are fewer elements failing before the peak strength, and the stress transfer and crack extension are inadequate. The brittle failure of rock becomes obvious as the homogeneity coefficient increases.

[1] YOU Ming-qing, ZOU You-feng. Discussion on heterogeneity of rock material and size effect on specimen strength [J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(3): 391-395. (in Chinese)

[2] TANG C A, LIU H, LEE P, TSUI Y, THAM L G. Numerical tests on micro-macro relationship of rock failure under uniaxial compression. Part I: Effect of heterogeneity [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(4): 555-569.

[3] LIU H Y, KOU S Q, LINDQVIST P A, TANG C A. Numerical modelling of the heterogeneous rock fracture process using various test techniques [J]. Rock Mechanics and Rock Engineering, 2007, 40(2): 107-144.

[4] LI Ming-tian, FENG Xia-ting, ZHOU Hui. 2D vector cellular automata model for simulating fracture of rock under tensile condition [J]. Key Engineering Materials, 2004, 261/262/263: 705- 710.

[5] LI Ming-tian, FENG Xia-ting, ZHOU Hui. Cellular automata simulation of interaction mechanism of two cracks in rock under uniaxial compression [J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(s1): 484-489.

[6] ZHOU Hui, LI Ming-tian, FENG Xia-ting, WANG Shi-min, WANG Yong-jia. A new meso-mechanical approach for modeling the rock fracturing process [J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(s1): 329-335.

[7] MA Zhi-tao, TAN Yun-liang, ZHANG Ting. Modeling of rock failure based on physical cellular automata [J]. Journal of Southeast University, 2005, 21(3): 348-352. (in Chinese)

[8] FENG Zeng-chao, ZHAO Yang-sheng, DUAN Kang-lian. Influence of rock cell characteristics and rock inhomogeneity parameter on complete curve of stress-strain [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(14): 2331-2335. (in Chinese)

[9] ZHU W C, LIU J, TANG C A, ZHAO X D, BRADY B H. Simulation of progressive fracturing processes around underground excavations under biaxial compression [J]. Tunnelling and Underground Space Technology, 2005, 20(3): 231-247.

[10] ZHU Wan-cheng, TANG Chun-an. Micromechanical model for simulating the fracture process of rock [J]. Rock Mechanics and Rock Engineering, 2004, 37(1): 25-56.

[11] WANG Xue-bin. Volume change of heterogeneous quasi-brittle materials in uniaxial compression [J]. Journal of Wuhan University of Technology: Materials Science Edition, 2006, 21(3): 162-167.

[12] WANG Xue-bin. Entire deformational characteristics and strain localization of jointed rock specimen in plane strain compression [J]. Journal of Central South University of Technology, 2006, 13(3): 300-306.

[13] FU Yu-fang. Numerical simulation of brittle rock failure process [D]. Shenyang: Northeastern University, 2000: 67-71. (in Chinese)

[14] LIANG Zheng-zhao. Three-dimensional failure process analysis of rock and associated numerical tests [D]. Shenyang: Northeastern University, 2005: 83-88. (in Chinese)

[15] LIU H Y, ROQUETE M, KOU S Q, LINDQVIST P A. Characterization of rock heterogeneity and numerical verification [J]. Engineering Geology, 2004, 72(1/2): 89-119.

[16] LIU H Y, KOU S Q, LINDQVIST P A, TANG C A. Numerical studies on the failure process and associated microseismicity in rock under triaxial compression [J]. Tectonophysics, 2004, 384(1/2/3/4): 149-174.

[17] FENG Xia-ting, PAN Peng-zhi, ZHOU Hui. Simulation of the rock microfracturing process under uniaxial compression using an elasto-plastic cellular automaton [J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(7): 1091-1108.

[18] PAN P Z, FENG X T, HUDSON J A. Study of failure and scale effects in rocks under uniaxial compression using 3D cellular automata [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(4): 674-685.

[19] MOGI K. Earthquake prediction [M]. Tokyo: Academic Press, 1985: 20-123.

[20] TANG Chun-an. Numerical simulation of AE in rock failure [J]. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(4): 368-374. (in Chinese)

[21] LIANG Zheng-zhao, TANG Chun-an, HUANG Ming-li, FU Yu-fang. Numerical simulation of patterns of acoustic emission in rock failure process [J]. Journal of Northeastern University, 2002, 23: 1008-1011. (in Chinese)

[22] Itasca Consulting Group. FLAC3D user’s manual (Version 3.0) [M]. Minneapolis, Minnesota: Itasca Consulting Group Inc, 2005.

[23] CAI M, KAISE P K, TASAKA Y, MINAMI M. Determination of residual strength parameters of jointed rock masses using the GSI system [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(2): 247-265.

[24] CAI M, KAISER P K, MORIOKA H, MINAMI M, MAEJIMA T, TASAKA Y, KUROSE, H. FLAC/PFC coupled numerical simulation of AE in large-scale underground excavations [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(4): 550-564.

(Edited by CHEN Wei-ping)

Foundation item: Project(2007CB209407) supported by the National Basic Research Program of China; Project(50729904) supported by the National Natural Science Foundation of China

Received date: 2009-12-17; Accepted date: 2010-04-06

Corresponding author: LI Shu-cai, PhD, Professor; Tel: +86-531-88399179; E-mail: lishucai@sdu.edu.cn