公路隧道岩体质量分级的模糊层次分析法

鲁光银^{1, 3}，朱自强¹，李  华²，熊  瑛¹，韩旭理³

(1. 中南大学 信息物理工程学院，湖南 长沙，410083；

2. 成都地质矿产研究所，四川 成都，610081；

3. 中南大学 信息科学与工程学院，湖南 长沙，410083)

摘  要：建立公路隧道岩体质量分级的模糊层次分析法(AHP), 对影响公路隧道岩体质量分级的各因素进行分析和调整，建立层次关系，构造阶层结构；采用模糊理论建立正倒值矩阵，计算各因素权重，建立各因素评分准则，根据专家调查与力学试验等方式确定各因素得分，采用逻辑运算计算综合评分，进而评判隧道岩体级别；给出模糊层次分析法算法流程，应用于常德－张家界高速公路关口垭隧道(44个试验断面)，将评判结果与传统的RMR岩体分级结果进行对比分析。研究结果表明，采用本方法进行岩体分级，43个断面与开挖实际情况吻合，而采用RMR方法仅36个断面接近实际情况；公路隧道岩体质量分级的模糊AHP法克服了传统方法固定评价因素和固定评分方式的缺陷，可以动态地选取评价因素，减少评分的主观性，评价结果更接近工程实际，为隧道、地下工程、边坡等的岩体质量分级研究提供了一种新的思路。

关键词：公路；隧道；岩体质量分级；模糊AHP法

中图分类号：U452.12         文献标识码：A         文章编号：1672-7207(2008)02-0368-07

Rock mass classification method in highway tunnel based on fuzzy analytic hierarchy process

LU Guang-yin^{1, 3}, ZHU Zi-qiang¹, LI Hua², XIONG Ying¹, HAN Xu-li³

 (1. School of Info-Physics and Geomatics Engineering, Central South University, Changsha 410083, China;

2. Chengdu Institute of Geology and Mineral Resources, Chengdu 610081, China;

3. School of Information Science and Engineering, Central South University, Changsha 410083, China)

Abstract: A method of rock mass classification in highway tunnel based on fuzzy analytic hierarchy process(AHP) was established. AHP method was used to construct the hierarchy relationship with factors of rock mass and their hierrarchy structures was set up. The weight of every factor was computed based on the positive reciprocal matrix using fuzzy sets method. The evaluation criteria of every factor and rock mass classification were constituted. After all grades were acquired by means of geological investigations and mechanical experiment, the rating of rock mass was calculated according to grading synthetically by iterative logical arithmetic. The arithmetic flow of the method was put forward, and the proposed method was applied to Guankouya tunneling(44 sections) along with Changde—Zhangjiajie Highway in Hunan province. The results show that the determined results are in a good agreement with those of the actual rock mass. 43 sections by the proposed method are accorded with actual sections, but only 36 sections by RMR. The proposed method can overcome the limitation of fixed factors and fixed mode of grading existing in traditional methods, acquire the effect factors dynamically, minimize judgmental bias, provide a quantitative measure of rock mass, and make the result more acceptable to the engineering fact, which offers a new thought to the research of rock mass classification method in such engineering fields as highway tunnelling, slope and underground project.

Key words: highway; tunnels; rock mass classification; fuzzy analytic hierarchy process

公路隧道设计和施工阶段必不可少的岩体质量分级，不仅对隧道岩体结构特征及其强度特性做出评价，还可以为支护方案的选取提供基础资料^[1]。目前, 国内外所使用的隧道岩体分级方法(如RMR法、RQD系统等)大多采用固定评价因素和固定评分方式，将影响岩体质量的各因素进行简单描述，再加以量化进行评分和分级，而没有考虑到影响隧道岩体质量分级的因素，具有不确定性、复杂性和模糊性等特征，无法表现出细微差异，常常导致评估结果与实际情形不同，存在较大局限性^[2]。针对这些问题，一些学者^[3-11]进行了研究，如郝哲等^[3-6]提出模糊综合评判方    法，S. A. I. Tzamos^[7]在Q分类中引入模糊数学和统计方法，J. S. Choi等^[8]提出利用电阻率参数的方法，这些方法在减少人为因素影响方面取得了一定效果。但由于影响隧道岩体质量分级的因素是多方面、多层次的，且每个因素的影响程度各不相同，而这些因素又相互关联、相互制约，致使这些方法还不能很好地用于指导现场设计、施工^[12]。为此，本文作者通过剖析影响公路隧道岩体分级的各种定性和定量因素，建立公路隧道岩体质量分级的模糊AHP法，以期为公路隧道施工中定量判定岩体级别提供理论依据并指导施工，也可为地下工程、边坡等岩体质量分级提供参考。

1  模糊AHP法模型

采用层次分析法^{[9, 13]}能够弹性地增加或减少评估因素，克服传统隧道岩体分级方法中评估因素固定而忽略了某些重要因素的缺点；另外，通过专家评估的方式调整各因素的权重，又可以解决传统岩体分级方法中固定评分方式存在的缺点，减少评估结果与实际情况之间的差异。考虑到传统的AHP法中将决策者主观认定的数值或相对重要性的不精确值当作精确值来处理，造成评估结果与现实结果存在较大差距的局限，引入模糊数学理论^[14-15]来解决这个问题，这2种方法相结合就是模糊AHP法^[16]，其结构如图1所示。针对隧道岩体质量分级的模糊AHP法步骤如下。

步骤1  建立层次结构。按照AHP法，根据隧道具体情况，从工程条件、地质条件、环境因素等方面确定影响隧道岩体质量分级的一级因素集、二级因素集等，建立反映这些因素之间的层次关系, 构造阶层结构。

图1  模糊层次分析法结构图

Fig.1  Structure map of fuzzy AHP

步骤2  建立成对比较矩阵。结合隧道实际情况，通过专家调查、现场测试、力学试验等多种手段，获得某一层次中影响因素间的两两相对重要性程度，建立成对比较矩阵B_ij。以第1层次中地质条件(a₁)、环境因素(a₂)和工程条件(a₃)三因素为例，假设环境因素对隧道岩体质量分级影响的重要程度为地质条件的3倍，地质条件为工程条件的2倍，环境因素为工程条件的6倍，则按地质条件、环境因素、工程条件顺序排列，建立的成对比较矩阵为：

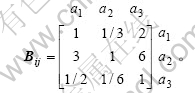
步骤3  计算三角模糊数。采用模糊理论综合专家的主观意见，确定成对比较矩阵中各元素取值。本模型采用三角模糊数整合专家意见，并表示所有专家对两两因素评分的模糊性。

步骤4  建立模糊正倒值矩阵。建立三角模糊数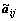来表达所有专家意见，进一步建立模糊正倒值矩阵：

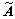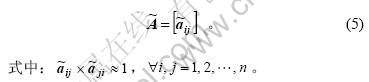
步骤5  计算影响隧道岩体分级各因素的模糊权重和综合评判模糊权重。采用J. J. Buckley^[17]提出的几何平均模糊权重法计算模糊成对比较矩阵中因素的模糊权重，这样既考虑了一致性指标，又达到了正规化的要求。

步骤6  计算隧道岩体质量分级的总评分。根据在建立岩体质量影响因素阶层结构时制订的评分准则，在求出各评估因素的模糊权重后，采用迭代逻辑运算求出岩体质量分级的总评分。

步骤7  岩体质量分级。建立隧道岩体质量分级参考表(表1)^[12]，根据岩体质量分级的总评分，对岩体质量进行分级评价。算法流程图如图2所示。

表1  岩体质量分级参考表

Table 1  Reference table of rock mass classification

图2  模糊AHP法流程图

Fig.2  Process map of fuzzy AHP method

2  算  例

常德—张家界高速公路关口垭隧道，净宽11.1 m，净高7.1 m，埋深10~71 m。主要岩层为志留系下统龙马溪浅海相泥质页岩，泥质结构，页理构造，局部含炭质，岩性较软，出露地表易风化，具明显的遇水崩解、失水干裂性质，山坡表面大多风化强烈，隧道洞身弱风化。受喜马拉雅运动影响，隧道内水平挤压作用强烈，次级褶皱发育，一般呈舒缓波状，揉皱和扭曲现象多见，低序次小断层也相当发育，岩层总体产状为300?~25?∠10?~25?, 节理发育至非常发育。另外，顺岩层面常见构造应力在岩层面集中形成的层间错动挤压夹泥带，厚度一般为0.5~20 cm，断续分布，泥层性质软弱^[18]。为便于研究，选取关口垭隧道的左洞  73 km+598 m~74 km+458 m路段(共44个断面，断面间距20 m左右，为了便于绘图，以73+598表示里程73 km+ 598 m)为研究对象进行分析研究。

3  计算与结果分析

3.1  评估因素的选取

隧道岩体分级评估因素的选择以隧道围岩的稳定性为出发点，分析前人研究中所选取的围岩稳定性因素^{[1-10, 12]}，大致上可分为诱发因素和潜在因素2种，主要为对围岩本身产生影响或造成围岩破坏的不稳定因素，如岩性、强度、节理等。

关口垭隧道工程地质条件是：浅埋，主要岩层为页岩，而页岩具有遇水易崩解的不良工程性质。因  此，评估因素的选取除考虑工程因素、地质因素    外，还需考虑隧道埋深、降雨量等环境因素。结合文献成果^{[1-10, 12]}，本方法中工程因素选取跨度、埋深等，环境因素选取地下水、雨量、灾害史等；地质构造因素选择节理面粗糙度、结构面间距、结构面与隧道轴向关系和填充物状况等；岩性选取岩石的单轴抗压强度、质量指标和岩石种类等。按照AHP法，建立如图3所示的岩体质量分级阶层结构。

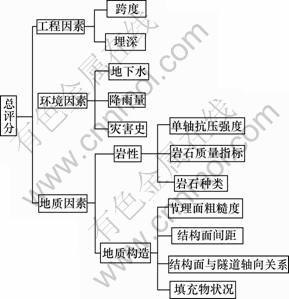
图3  岩体质量分级阶层结构

Fig.3  Hierarchy structure of rock mass classification

3.2  模糊权重的计算

建立阶层结构后，根据式(1)~(7)，通过几何平均方式求出各因素权重。针对一级因素集(地下水、降雨量、灾害史)，通过专家调查、现场试验^[18]等多种手段，采用模糊理论建立模糊正倒值矩阵：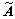

一级影响因素集(地下水、降雨量、灾害史)的相对权重计算过程如下。

a.        将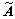分解为3个矩阵：

b.        计算各列的几何平均值：

c.        计算各因素的权重：

于是，3个因素的模糊权重为：

；

；

。

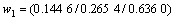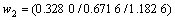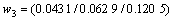d.        采用几何平均法将模糊权重值整合、正规化，计算各因素明确的权重：

e.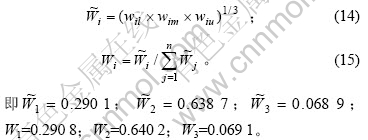       

经计算，一级因素集(地下水，降雨量，灾害史)的相对权重则为(0.290 8, 0.640 2, 0.069 1)。同理可得，一级因素集(跨度，埋深)的相对权重为(0.417, 0.583)， 一级因素集(单轴抗压强度，质量指标，岩石种类)的相对权重为(0.424, 0.240, 0.336)，一级因素集(节理面粗糙度，结构面间距，结构面与隧道轴间关系，填充物状况)的相对权重为(0.247, 0.362, 0.198, 0.193)，二级因素集(岩性，地质构造)的相对权重为(0.459, 0.541)，三级因素集(工程因素，环境因素，地质因素)的相对权重为(0.361, 0.160, 0.479)。

3.3  评分准则的建立

计算影响隧道岩体质量分级因素的模糊权重后，需要给阶层结构中的一级因素建立评分准则。结合文献^{[1, 3-9, 11-12]}成果，本模型采用分级评分的方式，输入值取0~10分，各因素具体的评分准则如表2所示。

3.4  结果与对比分析

建立评分准则之后，经过资料查询、专家调查、力学试验、现场测试^[17-18]等获取每个因素的实际分值，计算隧道岩体每一断面的评分；根据隧道岩体质量分级参考表(表1)评判岩体级别。为评价应用效果，在采用本方法对关口垭隧道岩体进行评价分级的同时，也采用目前常用的RMR方法进行岩体分级，并绘制评分结果对比图与岩体分级对比图。

图4所示为采用模糊AHP分级方法与RMR分级方法的评分结果对比图。可以看出，采用本方法对关口垭隧道左洞的44处断面岩体进行分析所得评分值与采用RMR法所得评分值差异不大，总的来说两者的评分情况基本一致，但部分地段如73＋(878~898)，74+(178~198)，74+(298~318)的评分结果相差较大，其中在74＋318地段评分差距最大，达29分。其原因主要是该断面地下水丰富，岩体结构面产状及其与洞轴线的组合关系非常不利(洞室轴向)，结构面充填物等因素在计算评分时本方法权重相对较大。

图4  隧道岩体模糊AHP分级与RMR分级评分结果

对比分析

Fig.4  Grading of rock mass classification comparison between Fuzzy AHP and RMR

表2  隧道岩体质量分级评分准则

Table 2  Evaluation criteria of tunnel rock mass classification

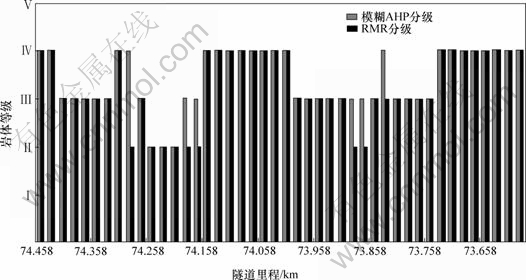
图5  隧道岩体模糊AHP分级与RMR分级结果对比分析

Fig.5  Rating of rock mass classification comparison between Fuzzy AHP and RMR

图5所示为采用模糊AHP分级方法与RMR分级方法的分级结果对比图。可以看出，采用本模型对关口垭隧道左洞的44处断面岩体分级所得结果与采用原RMR法所得结果基本一致，但在73＋(878~898)，73＋998~74＋018，74+(178~198)和74+(298~318)地段，岩体分级结果不一致，主要是模糊AHP岩体分级结果较差(Ⅳ、Ⅲ)，而采用RMR分级结果稍好(Ⅲ、Ⅱ)。

与开挖实际情况对比分析可知，对于73+(878~898)地段，采用模糊AHP法的分级结果为Ⅲ级，实际情况为Ⅳ级，略有所不同；而采用RMR法的分级为Ⅱ级, 差别更大。除此之外，采用本文研究方法的分级结果与实际情况大多吻合，均为Ⅲ~Ⅳ级。总体来说，采用本文方法所得分级结果较采用RMR法所得结果更接近隧道开挖实际情况。

4  结  论

a. 针对页岩地区浅埋隧道的具体特点，对我国现行“公路隧道岩体分级方法”分类指标进行分析整理，选取12个定性、定量指标，对44个试验断面进行岩体分级实践，采用模糊AHP法所得岩体分级结果有43个断面与实际情况吻合，而采用传统RMR方法仅36个断面接近实际情况。

b. 在工程实践中，根据隧道开挖情况，采用模糊AHP法进行隧道岩体分级，针对不同地质情况和岩体类别建立不同的层次构架，动态调整隧道岩体分级的因素，借助专家对各个评估因素之间的相对重要性进行评价，客观计算各因素权重，避免了权重因素确定的主观片面性，降低了人为因素影响，推动围岩分级由定性向定量发展。模糊AHP法理论体系完整，计算步骤明确，编程实现容易；工程实例也表明，模糊AHP法是一种简单易行的隧道岩体质量分级方法。

c. 影响隧道岩体分级因素多且复杂，不同的专家学者对于每个评价因素的影响程度意见不一。下一步研究重点应该针对不同类型隧道、不同岩体，收集足够的工程岩体分级记录，整理一套通用的隧道岩体分级阶层结构。在具体应用过程中，根据隧道工程实际情况进行修正，使其能够更广泛地适用于各种不同类型隧道的工程岩体分级。

参考文献：

[1] 王延平, 许 强, 高 霞. 岩体质量分级的模糊识别[J]. 水土保持研究, 2005(1): 108-109.
WANG Yan-ping, XU Qiang, GAO Xia. Fuzzy identification of the quality grading of rock bod[J]. Research of Soil and Water Conservation, 2005(1): 108-109.

[2] 陈昌彦, 王贵荣. 各类岩体质量评价方法的相关性探讨[J]. 岩石力学与工程学报, 2002, 21(12): 1894-1900.
CHEN Chang-yan, WANG Gui-rong. Discussion on the interrelation of various rockmass quality classification systems at home and abroad[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(12): 1897-1900.

[3] 郝 哲, 汪明元. 公路隧道岩体分级的模糊综合评判法[J]. 长江科学院院报, 2005, 22(5): 55-57.
HAO Zhe, WANG Min-yuan. Fuzzy synthesis assessment method for rock mass classification of highway tunnel[J]. Journal of Yangtze River Scientific Research Institute, 2005, 22(5): 55-57.

[4] 丁向东, 吴继敏. 岩体质量模糊分类法[J]. 水利水电科技进展, 2006, 26(3): 18-20.

DING Xiang-dong, WU Ji-min. Fuzzy classification of rock mass[J]. Advanced in Science and Technology of Water Resource, 2006, 26(3): 18-20.

[5] 白明洲, 许兆义, 王连俊. 隧道围岩分级的模糊信息分析模型及应用研究[J]. 铁道学报, 2001, 23(6): 85-88.
BAI Ming-zhou, XU Zhao-yi, WANG Lian-jun. Study and application on fuzzy information analysis model in tunnel surrounding rock mass classification[J]. Journal of the China Railway Society, 2001, 23(6): 85-88.

[6] Aydin A. Fuzzy set approaches to classification of rock masses[J]. Engineering Geology, 2004, 74(3/4): 227-245.

[7] Tzamos S A I. Extending the Q system’s prediction of support in tunnels employing fuzzy logic and extra parameters[J]. International Journal of Rock Mechanics & Mining Sciences, 2006, 43(3): 938-949.

[8] Choi J S, Ryu H H, Cho G C. Electrical resistivity-based rock mass classification for tunneling[J]. Tunneling and Underground Space Technology, 2006, 21(3/4): 234.

[9] CHEN Chao-shi, LIU Ya-ching. A methodology for evaluation and classification of rock mass quality on tunnel engineering[J]. Tunnelling and Underground Space Technology, 2007, 22(3/4): 377-387.

[10] SEN Ze-kai, Bahaeldin H S. Modified rock mass classification system by continuous rating[J]. Engineering Geology, 2003, 67(3/4): 269-280.

[11] Pooyan A, Roozebeh F. Comparison of the evaluated rock mass properties from the TSP system and the RMR classification (Semnan tunnel, Iran)[J]. Tunnelling and Underground Space Technology, 2006, 21(3/4): 236.

[12] 李 华. 基于模糊AHP的隧道围岩分级方法研究[D]. 长沙: 中南大学信息物理工程学院, 2006.
LI Hua. Research of rock mass classification method in tunnel based on fuzzy AHP[D]. Changsha: School of Info-Physics and Geomatics Engineering, Central South University, 2006.

[13] 李军锋, 李天文. 基于层次分析法的秦岭地区大熊猫栖息地质量评价[J]. 山地学报, 2005, 23(6): 694-701.
LI Jun-feng, LI Tian-wen. The quality evaluation of giant panda’s habitat based on analytic hierarchy process[J]. Journal of Mountain Science, 2005, 23(6): 694-701.

[14] Gokceoglu C, Yesilnacar C, Sonmez H. A neuro-fuzzy model for modulus of deformation of jointed rock masses[J]. Computers and Geotechnics, 2004, 31(5): 375-383.

[15] Hsu H M, Chen C T. Aggregation of fuzzy opinions under group decision making[J]. Fuzzy Set and Systems, 1996, 79(3): 279-285.

[16] Hsu T H. Transportation project evaluations: A fuzzy measure AHP[J]. Proceedings of NSC, Part C, 1997, 7(1): 26-34.

[17] Buckley J J. Fuzzy hierachial analysis[J]. Fuzzy Sets and Systems, 1985, 17(3): 233-247.

[18] 鲁光银, 朱自强. 关口垭隧道综合超前地质探测报告[R]. 长沙: 中南大学信息物理工程学院, 2006.
LU Guang-yin, ZHU Zi-qiang. Report of synthetical geology exploration and prediction in Guankouya tunnel[R]. Changsha: School of Info-Physics and Geomatics Engineering, Central South University, 2006.

收稿日期：2007-06-10；修回日期：2007-08-20

基金项目：交通部西部交通建设科技项目(200231800021)；湖南省科技计划资助项目(05SK3077)

通信作者：鲁光银(1976-)，男，湖北宜昌人，博士，讲师，从事隧道灾害探测与评价技术研究；电话：13975894898；E-mail: 13975894898@139.com