DOI: 10.11817/j.issn.1672-7207.2019.03.017

动态地下水位变化引起的基坑底抗渗流稳定性计算新方法

章丽莎^{1, 2}，应宏伟²，王迪²，谢康和²

(1. 浙江大学城市学院 工程学院，浙江 杭州，310015；

2. 浙江大学 建筑工程学院滨海和城市岩土工程研究中心，浙江 杭州，310058)

摘要：针对地下水位动态变化条件下基坑工程的渗流稳定性问题，基于越流理论，给出基坑底靠近支护结构处的出逸比降解析解答，提出考虑非稳定渗流的基坑底抗渗流稳定性简化计算方法。通过算例计算，进行出逸比降的解析解正确性验证和影响因素分析，并将该方法应用于工程案例。研究结果表明：当基坑土体渗透系数较大时，考虑非稳定渗流的出逸比降解析解答与传统稳定渗流假定的结果一致，验证了解析解的正确性；出逸比降的影响因素可通过与土体渗透系数、压缩模量正相关，与地下水位变化的角频率和计算模型细粒土层总厚度的平方负相关的量纲一因子θ统一表示；在实际工程中，出逸比降与地下水位的变化不同步，应注意工程降水时出逸比降未能及时有效减小的情况，避免基坑工程的抗渗流破坏风险。

关键词：非稳定渗流；出逸比降；抗渗流稳定性；动态地下水位变化；基坑

中图分类号：TU463        文献标志码：A         文章编号：1672-7207(2019)03-0634-07

New method of excavation base seepage stability calculation due to dynamic varying groundwater level

ZHANG Lisha^{1, 2}, YING Hongwei², WANG Di², XIE Kanghe²

(1. School of Engineering, Zhejiang University City College, Hangzhou 310015, China;

2. Research Center of Coastal and Urban Geotechnical Engineering, College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China)

Abstract: To deal with the seepage stability of excavation under dynamic varied groundwater level condition, analytical solution of exit gradient in the excavation base near the retaining structure was derived based on leaky theory, and simplified method was proposed to calculate the excavation base seepage stability considering unsteady seepage. The validity of analytical solution was verified and the influential factors of exit gradient were analyzed based on idealized case studies. And then the proposed method was applied to the practical engineering case. The results show that if the coefficient of permeability of the excavation soil is large enough, the analytical solution results of exit gradient considering transient unsteady seepage are in agreement with the traditional results under the steady seepage assumption, which verifies the validity of the analytical solution; the influence factor of exit gradient is described by the dimensionless factor θ, which is positively correlated with the coefficient of permeability and the constrained modulus of the soil, but is negatively correlated with the angular frequency of groundwater level variation and the squared total thickness of the fine-grained soil in analytical model; the exit gradient variation is asynchronous with the groundwater level variation in practical projects, such situation should be avoided that the exit gradient can not reduce timely and efficiently through dewatering process to prevent seepage damage of the excavation project.

Key words: unsteady seepage; exit gradient; seepage stability; dynamic groundwater level variation; excavation

近年来，随着城市建设快速发展，深基坑工程日趋增多，基坑工程面临深度深、平面规模大、施工环境复杂以及施工难度大等挑战，特别是在滨海、沿江地区的深基坑工程更是面临复杂地下水作用可能引起的基坑变形过大和基坑失稳等风险，该类地区的深基坑设计须进行基坑抗渗流稳定性计算。目前，对基坑底的抗渗流稳定性计算多基于稳定渗流条件展开，规范和手册等^[1-3]通过坑内外水头差除以渗流路径获得基坑底的出逸比降，与临界水力坡降进行对比，使两者的比值满足一定的安全系数。在实际工程中，坑外地下水位将随着降雨、地下水的抽取和回灌、工程临近江河湖泊的水位变化等情况发生变化^[4-6]，当基坑土体为细粒土(粉土、黏土等)时，基坑土体中会发生非稳定渗流^[7]，对基坑的抗渗流稳定性产生一定的影响。大多数关于非稳定渗流作用下的基坑研究是通过有限元数值软件进行基坑变形^[8]和基坑整体稳定性^[9]等相关的计算和分析，较少涉及非稳定渗流条件下基坑底的抗渗流稳定性理论研究。在此，本文作者采用解析的方法研究坑外地下水位动态变化引起的基坑土体非稳定渗流对基坑底抗渗流稳定性的影响，提出考虑非稳定渗流的基坑底抗渗流稳定性简化计算方法。

1  传统的基坑底抗渗流稳定性计算方法

图1所示为滨海、沿江地区的基坑断面示意图，该类地区地基表层通常为具有强透水性的粗粒土或杂填土，下卧深厚透水性较弱的细粒土。沿基坑支护结构并绕过支护结构底部的地下水渗流路径最短，是最容易发生渗透破坏的位置之一，因此，以地下水位变化引起的沿支护结构的渗流作为主要研究对象，计算基坑底靠近支护结构处的抗渗流稳定性。

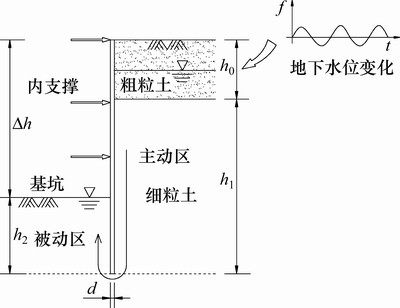
图1  动态变化地下水位作用下基坑断面示意图

Fig. 1  Schematic of excavation section under dynamic varied groundwater level

规范和手册等^[1-3]给出的基坑抗渗流稳定性验算指出，渗流的水力坡降不应超过临界水力坡降，如下式所示：

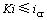                  (1)

式中：K为抗渗流稳定性验算的安全系数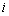；为渗流出口处水力坡降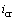；为临界水力坡降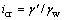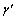，；和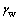分别为土体浮重度和地下水重度。

采用传统的方法^{[1-3, 10]}计算动态地下水作用下基坑底靠近支护结构处最危险的出逸比降(即开挖面处的水力坡降值) 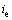时，一般不考虑地下水位变化引起的非稳定渗流对基坑底出逸比降的影响，认为地下水头变化在基坑中形成稳定渗流，出逸比降为坑内外水头差与最短渗流路径的比值：

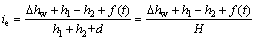   (2)

式中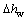：为原有恒定地下水位线至细粒土层顶面的距离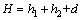；，h₁为主动区细粒土层厚度，h₂为被动区土层厚度，d为支护结构厚度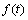；为坑外地下水位的变化值随时间变化的表达式，以原有恒定地下水位线为变化的起始点和平衡位置，其变化范围不应超越上覆粗粒土层的上下边界。

因此，采用传统方法进行动态地下水作用下基坑底抗渗流稳定性验算时，应满足

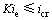                 (3)

事实上，地下水位动态变化将在细粒土层中引起非稳定渗流从而产生超静孔压，进而影响基坑底靠近支护结构处的出逸比降，与稳定渗流的情况存在较大差异。本文提出了考虑地下水位动态变化的基坑底抗渗流稳定性计算新方法：根据越流理论，求解非稳定渗流在细粒土中产生的超静孔隙水压力，获得地下水位动态变化引起的出逸比降变化值，结合原有恒定地下水位下稳定渗流的初始出逸比降，得到地下水位动态变化条件下基坑底靠近支护结构处的出逸比降，进行抗渗流稳定性验算。

2  基坑底抗渗流稳定性计算新方法

2.1  计算模型及基本假定

由于地下水绕支护结构底部的渗流是连续的，可以把沿支护结构底部的土体和基坑被动区假想为坑外主动区的底部，与主动区组成一个单层地基系统^{[4, 11]}，如图2所示。于是，地下水位变化引起的基坑细粒土层中沿支护结构的渗流可简化为一维非稳定渗流。

若基坑平面长度和宽度均较大且逐层开挖历时较长，则基坑开挖至某一工况时可认为原有地下水位在土体中已形成稳定渗流。为简化分析，主要研究基坑开挖至某一工况时在原有恒定地下水位条件下发生地下水位动态变化引起的基坑底抗渗流稳定性问题。暂不考虑被动区土体卸荷效应、加固作用等影响，将表征基坑主动区和被动区土体基本物理性质、力学特性相关的土性参数取值相同。由于上覆粗粒土的渗透系数远大于下卧细粒土的渗透系数，可暂不考虑粗粒土层中渗流引起的水头损失^[7]，粗粒土层底部作用于模型细粒土层上部边界的水压力近似地取为水头压力。当上覆粗粒土层的饱和重度与天然重度差别很小时，可忽略不计，即不考虑上覆粗粒土层中的地下水位变化引起的下卧深厚细粒土层中总应力的变化，于是，可将粗粒土层中地下水位变化以边界孔压变化的形式作用于下卧细粒土层的上部边界。

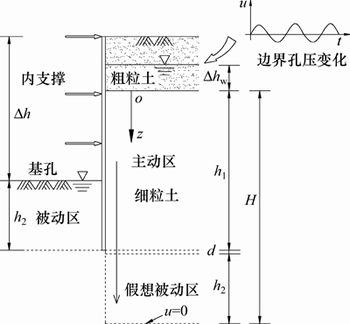
图2  动态变化地下水位作用下基坑底抗渗流稳定性计算的简化模型

Fig. 2  Simplified model for seepage stability calculation of excavation base under dynamic varied groundwater level

基于以上计算模型的基本假定，得到地下水位动态变化引起的超静孔压u在细粒土层中沿支护结构的传播控制方程为

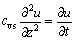                (4)

式中：为土的固结或回弹系数，暂不考虑水位动态变化过程中地基的回弹，直接取为固结系数并假定为常数；z为深度方向；t为时间；u为超静孔压。

本文计算模型中细粒土层的顶部边界取为地下水压力的变化值随时间动态变化的表达式，其边界条件可表示为

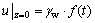             (5)

计算模型底部边界(即基坑底开挖面)为透水边界，其边界条件的表达式为

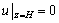 (底面透水)          (6)

初始条件为

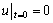                (7)

2.2  超静孔压解析计算

首先，将计算模型顶部边界条件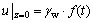按傅里叶级数形式展开：

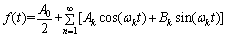    (8)

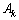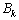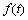式中：和为傅里叶级数展开后的各个简谐波动分量的幅值，(取k=1, 2, 3, …)为相应的波动角频率，T为的周期。波幅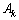和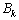由傅里叶系数公式解得：

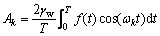          (9)

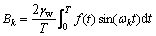         (10)

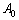可由式(9)取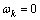得到：

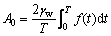             (11)

如上所述，计算模型顶部孔压边界可由若干个简谐波动分量叠加而成；根据已有研究^{[4, 12]}可知，简谐波动分量对应的超静孔压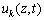的解析表达式如下：

      (12)

式中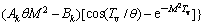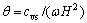，； ；，为量纲一因子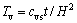；，为时间影响因子。

将各个简谐波动分量对应的超静孔压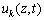叠加后得到本文求解的超静孔压u的解析表达式：

      (13)

式中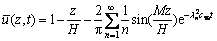：，通过已有研究^{[8, 10]}的解答直接获得。

2.3  出逸比降解析计算

根据水力坡降的定义^[13]，可求得地下水位动态变化引起的基坑底靠近支护结构处出逸比降变化值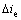，其表达式如下：

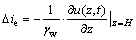        (14)

式中，由式(13)得到。

原有恒定地下水位对应的初始出逸比降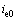为

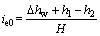            (15)

将地下水位动态变化引起的出逸比降变化值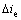和原有恒定地下水位对应的初始出逸比降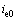叠加，得到动态变化地下水位作用下基坑底靠近支护结构处出逸比降为

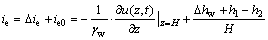  (16)

所求得的动态变化地下水位作用下基坑底靠近支护结构处出逸比降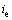应满足式(3)。

对本文解析解答的适用条件和具体应用进行如下说明：

1) 本文采用傅里叶级数展开的方法求解地下水位动态变化在细粒土中产生的超静孔隙水压力的解析表达式，因此地下水位变化函数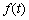需满足能够进行傅里叶级数展开的条件。

2) 由于模型顶部边界条件(5)并不满足控制方程式(4)，使得式(13)求解得到的超静孔压u仅适用于当0＜z≤H的情况，但当z无限趋近于z=0时该解仍适用。为求解方便，可由边界条件(5)直接确定z=0处超静孔隙水压力u。

3  计算与分析

3.1  出逸比降解析解的验证

已有研究表明^[4-6]，当土体的渗透系数较大时，坑外地下水位变化引起的计算模型边界孔压变化将在基坑土体中迅速传播，可能来不及产生超静孔压就已经形成稳定渗流，在该情况下，本文方法给出的基坑底靠近支护结构处出逸比降的解答与传统方法的计算结果一致。为验证本文方法求得的出逸比降解析解答的正确性，按照上述思路设计算例：假设计算模型中的土体为中粗砂，渗透系数可取k_v=1 mm/s^[14-16]，压缩模量E_s=10 MPa；上覆粗粒土层厚度h₀=6 m，原有恒定地下水位线至细粒土层顶面的距离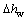=3 m，地下水位变化引起的边界孔压变化方程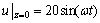，即地下水位变化形式取为正弦波动形式，幅值为2 m，其中取波动周期为1 d；基坑主动区细粒土层厚度h₁=10 m，被动区细粒土层厚度h₂=8 m，支护结构厚度d=1 m。出逸比降解析解验证如图3所示，本文给出的出逸比降计算结果与传统方法的求解结果一致，验证了解析解的正确性。

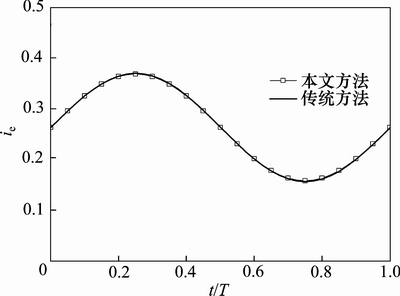
图3  出逸比降解析解验证

Fig. 3  Verification of analytical solution for exit gradient

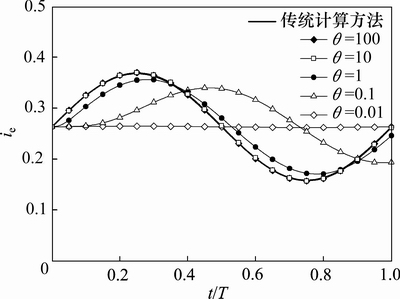
图4  不同θ对应的出逸比降随时间变化曲线

Fig. 4  Variation curve of exit gradient against time with different θ

3.2  出逸比降的影响因素

由出逸比降解析解的形式可知，出逸比降与计算模型土体总厚度、细粒土的渗透系数和压缩模量、地下水位变化周期等因素相关，可通过量纲一因子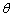统一表示，故本节讨论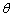对动态地下水作用下基坑底靠近支护结构处出逸比降的影响规律。为简化分析，计算模型中上覆粗粒土层厚度h₀=6 m，基坑主动区细粒土层厚度h₁=10 m，被动区细粒土层厚度h₂=8 m，支护结构厚度d=1 m，原有恒定地下水位线至细粒土层顶面的距离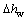=3 m，地下水位变化引起的细粒土层上部孔压边界的波动方程设为。

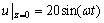不同θ对应的出逸比降随时间变化曲线如图4所示。从图4可以发现：基坑底靠近支护结构处出逸比降随时间的变化曲线受θ的影响明显，θ越大，出逸比降的变化幅值衰减越少，相位差越小；当θ大于某一数值时(如θ=10, 100)，本文方法求解的出逸比降计算结果与传统方法求得的结果基本吻合，不存在变化幅值衰减、相位差或滞后性等现象；当θ较小时(如θ=0.1)，出逸比降变化幅值较小，其波形也存在明显的相位差；当θ很小时(如θ=0.01)，出逸比降受地下水位变化的影响不明显或几乎不受地下水位变化的 影响。

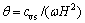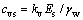由式和可知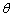，与土体渗透系数、压缩模量正相关，与地下水位变化的角频率和计算模型细粒土层总厚度的平方负相关。结合图4可知，当计算模型细粒土层的总厚度一定时，土体渗透系数、压缩模量或地下水位变化周期越大，出逸比降的变化越明显，变化幅值越大，相位差越小，滞后性越不明显。

在实际工程中，土体渗透系数的变化范围较大，对于渗透性极好的细粒土，动态地下水位变化在计算模型的细粒土层中将不产生超静孔压的影响，可采用传统计算方法求解基坑底的出逸比降，进行抗渗流稳定性验算。一般而言，细粒土的渗透系数普遍比较小(例如黏土、淤泥土等)，使得计算模型的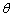较小，从而导致出逸比降的变化幅值衰减较大，同时存在明显相位差和滞后现象。此时，当基坑开挖过程中进行工程降水时，需充分重视坑外地下水位下降，但基坑底土体的出逸比降减小幅度不大且滞后对实际基坑工程抗渗流稳定性的影响。

3.3  工程应用

采用杭州下沙某一基坑工程为例进一步说明本文提出的动态地下水作用下基坑底抗渗流稳定性简化计算方法在实际工程中的具体应用。参考图1所示的基坑断面，该基坑的围护桩采用直径为0.9 m、入土深度为23.35 m的钻孔灌注桩，其后设置单排直径为0.85 m、入土深度为20.75 m的三轴水泥搅拌桩隔水帷幕, 故支护结构的计算厚度应取d=1.75 m；该基坑计算模型中基坑支护结构的入土深度以水泥搅拌桩的入土深度(隔水深度)为准，上覆粗粒土厚度h₀=8.4 m，基坑底靠近支护结构处的开挖深度为11.75 m，故基坑主动区细粒土层厚度h₁=12.35 m，被动区细粒土层厚度h₂=9 m；计算模型中的细粒土为砂质粉土，渗透系数k_v=2×10^-6 m/s，压缩模量E_s=12 MPa。开挖前，通过工程降水将地下水位降至距细粒土层顶面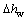= 1.4 m，保持地下水位不变，进行基坑分层开挖。由于基坑开挖完成时值杭州梅雨季，某次大型降雨导致基坑外地下水位快速升高，施工单位采取紧急降水措施后，地下水位又回落至工程降水设计水位线位置，此次地下水位变化的示意图如图5所示，地下水位的变化高度为4.5 m，变化周期T取为1 d，即T=86 400 s，因此，计算模型中细粒土层上部孔压变化的边界条件可采用如下数学表达式表示：

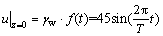          (17)

采用傅里叶级数展开的方法求解式(17)，由式(9)~(11)求解得到A_k=0 (其中，k=0, 1, 2, 3, 4, …)，B₁=45，B_k=0 (其中，k=2, 3, …)，均代入式(13)得到：

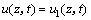                  (18)

式(18)中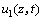，为A₁=0，B₁=45 kPa时式(12)的解答。

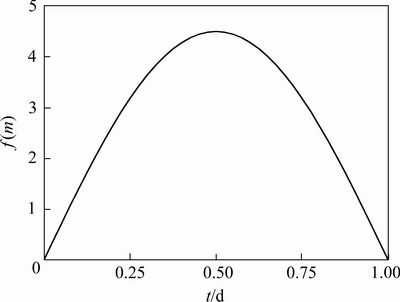
图5  某工程地下水位变化示意图

Fig. 5  Schematic of groundwater variation in a project

根据以上参数可计算基坑底靠近支护结构处的出逸比降随时间变化情况等计算结果。

图6所示为该工程降雨及降水引起的地下水位变化情况下的出逸比降的本文方法和传统方法的求解结果，并与地下水位保持不变情况下的出逸比降解答对比。从图6可以发现：采用本文方法的出逸比降计算结果与传统方法的结果存在较大差异；在地下水位上升初期，本文方法计算的基坑底靠近支护结构处的出逸比降几乎无变化，与地下水位不变情况下的出逸比降解答基本一致；在地下水位上升后期及降水过程中，本文方法计算的出逸比降逐渐增大；由于工程降水完成后，地下水位变化引起的细粒土中的超静孔压将不断消散，出逸比降也将不断减小，可认为工程降水完成时本文方法求解的出逸比降达到最大值。该现象可以通过图4进行阐释。对于该工程情况而言，由于细粒土为粉土，其渗透系数较小，计算得到θ ≈ 0.062，使得出逸比降的最大值为0.3，较传统方法计算得到的最大出逸比降值0.4有所减小且存在明显的滞后现象。《基坑工程手册》^[3]认为：安全系数K的取值不应小于2，取K=2，粉土的i_cr约为0.8，满足式(3)，此次工程降水可有效预防基坑发生抗渗流稳定性破坏。

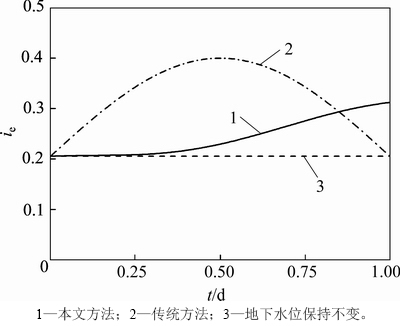
图6  出逸比降随时间变化示意图

Fig. 6  Schematic of exit gradient variation with time

通过以上工程算例分析可以发现：由于透水性较弱的细粒土的越流作用，导致地下水位升高引起细粒土中的超静孔压缓慢增加，使得基坑底靠近支护结构处的出逸比降并未随地下水位的变化发生同步变化。对于某些大型基坑工程，其平面长度和宽度均较大、开挖深度深，一般采用分级降水后进行分层开挖，建议在降坑外地下水方案设计时考虑细粒土层的越流特性，特别注意工程降水引起坑外地下水位下降但基坑底出逸比降的减小幅度不大并存在明显滞后性的情况，避免基坑工程的抗渗流破坏风险。

4  结论

1) 坑外地下水位动态变化将引起非稳定渗流从而影响基坑底靠近支护结构处的出逸比降，与基于稳定渗流假定的出逸比降计算结果存在较大差异，应进行考虑非稳定渗流的基坑底抗渗流稳定性验算；当细粒土的渗透系数较大时，坑外地下水位变化引起的计算模型边界孔压变化将在细粒土中迅速传播形成稳定渗流，可采用传统方法计算基坑底的抗渗流稳定性。

2) 考虑非稳定渗流的基坑底靠近支护结构处出逸比降的影响因素，可通过与土体渗透系数、压缩模量正相关，与地下水位变化的角频率和计算模型细粒土层总厚度的平方负相关的量纲一因子θ统一表示。当θ较大时，本文方法计算得到的出逸比降与传统方法的计算结果一致，不存在变化幅值衰减、相位差或滞后性等现象；随着θ减小，出逸比降的变化幅值将不断衰减，出现明显的滞后性。

3) 当细粒土的透水性较弱时，由于越流作用，导致地下水位变化引起细粒土中的超静孔压缓慢地传播，基坑底靠近支护结构处的出逸比降与地下水位的变化不同步。在实际工程降坑外降地下水设计时，应考虑基坑土体的越流特性，还需注意工程降水引起坑外地下水位下降但基坑底的出逸比降未及时减小的情况，避免基坑工程的抗渗流破坏风险。

参考文献：

[1] GB 50007—2011, 建筑地基基础设计规范[S].

GB 50007—2011, Code for design of building foundation[S].

[2] DG/TJ 08-61—2010, 基坑工程技术规范[S].

DG/TJ 08-61—2010, Technical code for excavation engineering[S].

[3] 刘国彬, 王卫东. 基坑工程手册[M]. 北京: 中国建筑工业出版社, 2010: 144, 240-243.

LIU Guobin, WANG Weidong. Excavation engineering handbook[M]. Beijing: China Architecture and Building Press, 2010: 144, 240-243.

[4] 应宏伟, 章丽莎, 谢康和, 等. 坑外地下水位波动引起的基坑水土压力响应[J]. 浙江大学学报(工学版), 2014, 48(3): 492-497.

YING Hongwei, ZHANG Lisha, XIE Kanghe, et al. Pore and earth pressure response to groundwater fluctuation out of foundation pit[J]. Journal of Zhejiang University (Engineering Science), 2014, 48(3): 492-497.

[5] ZHANG Lisha, YING Hongwei, XIE Kanghe, et al. Effect of groundwater fluctuations on pore pressures and earth pressures on coastal excavation retaining walls[J]. Marine Georesources & Geotechnology, 2016, 34(8): 770-781.

[6] 章丽莎. 滨海地区地下水位变化对地基及基坑渗流特性的影响研究[D]. 杭州: 浙江大学建筑工程学院, 2017: 13-37.

ZHANG Lisha. Study on the influence of groundwater table variation on the seepage behavior of foundation and excavation in coastal area[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2017: 13-37.

[7] 龚晓南, 高有潮. 深基坑工程设计施工手册[M]. 北京:中国建筑工业出版社, 1998: 39.

GONG Xiaonan, GAO Youchao. Deep excavation engineering design and construction handbook[M]. Beijing: China Architecture and Building Press, 1998: 39.

[8] 刘婧. 深基坑边降水边开挖的变形特性研究[D]. 上海: 上海交通大学船舶海洋与建筑工程学院, 2010: 9-40.

LIU Jing. The deformation characteristics analysis of deep foundation pit while dewatering and excavation considered simultaneously[D]. Shanghai: Shanghai Jiao Tong University. School of Naval Architecture, Ocean and Civil Engineering, 2010: 9-40.

[9] 张庆伟. 非稳定渗流作用下基坑支护结构稳定性分析[D]. 郑州: 郑州大学土木工程学院, 2007: 58-65.

ZHANG Qingwei. Stable analysis of foundation pit retaining structure under unsteady seepage[D]. Zhengzhou: Zhengzhou University. School of Civil Engineering, 2007: 58-65.

[10] 李广信. 高等土力学[M]. 北京: 清华大学出版社, 2012: 5-20.

LI Guangxin. Advanced soil mechanic [M]. Beijing: Tsinghua University Press, 2012: 5-20.

[11] LI Yuqi, YING Hongwei, XIE Kanghe. On the dissipation of negative excess porewater pressure induced by excavation in soft soil[J]. Journal of Zhejiang University(Engineering Science), 2005, 6A(3): 188-193.

[12] CONTE E, TRONCONE A. Soil layer response to pore pressure variations at the boundary[J]. Géotechnique, 2008, 58(1): 37-44.

[13] TERZAGHI K, PECK R B, MESRI G. Soil mechanics in engineering practice[M]. New York: John Wiley & Sons, 1996: 71-72.

[14] 毛昶熙, 段祥宝, 吴良骥. 砂砾土各级颗粒的管涌临界坡降研究[J]. 岩土力学, 2009, 30(12): 3705-3709.

MAO Changxi, DUAN Xiangbao, WU Liangji. Study of critical gradient of piping for various grain sizes in sandy gravels[J]. Rock and Soil Mechanics, 2009, 30(12): 3705-3709.

[15] 王俊杰, 卢孝志, 邱珍锋, 等. 粗粒土渗透系数影响因素试验研究[J]. 水利水运工程学报, 2013(6): 16-20.

WANG Junjie, LU Xiaozhi, QIU Zhenfeng, et al. Experimental studies on influence factors of permeability coefficients of coarse-grained soil[J]. Hydro-Science and Engineering, 2013(6): 16-20.

[16] 苏立君, 张宜健, 王铁行. 不同粒径级砂土渗透特性试验研究[J]. 岩土力学, 2014, 35(5): 1289-1294.

SU Lijun, ZHANG Yijian, WANG Tiexing. Investigation on permeability of sands with different particle sizes[J]. Rock and Soil Mechanics, 2014, 35(5): 1289-1294.

(编辑  赵俊)

收稿日期：2018-03-25；修回日期：2018-05-15

基金项目(Foundation item)：国家自然科学基金资助项目(51678523，51338009) (Projects(51678523, 51338009) supported by the National Natural Science Foundation of China)

通信作者：应宏伟，博士，副教授，从事地基处理和基坑工程方面的研究；E-mail：ice898@zju.edu.cn