J. Cent. South Univ. Technol. (2010) 17: 437-442

DOI: 10.1007/s11771-010-0503-7                                                                                                                                                  

Effect of interaction of dislocations with core-shell nanowires on

critical shear stress of nanocomposites

FANG Qi-hong(方棋洪)^{1, 2}, LIU Yong(刘咏)², LI Hui-zhong(李慧中)², HUANG Bo-yun(黄伯云)²

1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University,

Changsha 410082, China;

2. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2010

Abstract: The contribution to the critical shear stress of nanocomposites caused by the interaction between screw dislocations and core-shell nanowires (coated nanowires) with interface stresses was derived by means of the MOTT and NABARRO’s model. The influence of interface stresses on the critical shear stress was examined. The result indicates that, if the volume fraction of the core-shell nanowires keeps a constant, an optimal critical shear stress may be obtained when the radius of the nanowire with interface stresses reaches a critical value, which differs from the classical solution without considering the interface stresses under the same external conditions. In addition, the material may be strengthened by the soft nanowires when the interface stresses are considered. There also exist critical values of the elastic modulus and the thickness of surface coating to alter the strengthening effect produced by it.

Key words: nanocomposites; dislocations; nanowire; interface stress; critical shear stress

1 Introduction

Nanocomposite solids may have higher strength and hardness, higher thermal stability and better electrical conductivity than their conventional counterparts. Special interest is the behavior of nanocomposites with ensembles of nanoparticles and nanowires [1-3], due to their importance for high technologies based on nanostructures with the complicated architecture as well as for understanding the basic nature of nanoscale effects in composite solids.

For the understanding of strengthening mechanisms in a number of alloys and composites, the elementary interaction between a single inclusion and a dislocation on the nearby slip plane will be first considered, which leads to an interaction force acting on the dislocation. Considering its importance, the interaction of a dislocation (screw or edge dislocation) with an inclusion had received much attention in the past of decades [4-10]. In recent years, nanocomposites containing coated nanowires embedded into a matrix have drawn significant interest with the rapid development of nanotechnology [11]. Among the nanostructured materials, nanochannel-array materials have been extensively used in nanotechnology. They can not only be used as filters and catalysts, but also as templates for nanosized structures, such as magnetic, electronic, and optoelectronic devices [12]. These nanostructured materials can be strengthened by the surface coating  [13]. Therefore, the study on the strengthening mechanisms of the composites containing coated nanowires (core-shell nanowires) or nanoholes with surface coatings is important.

A great number of possible strengthening mechanisms were discussed [14]. The modulus mismatch strengthening is an important strengthening mechanism that arises from the difference of elastic moduli in the matrix and the inclusion. RUSSELL and BROWN [15] gave an approximate expression for the critical resolved shear stress of the material strengthened by a modulus difference between matrix and precipitate. The interaction force acting on the dislocation owing to the interaction between a spherical precipitate and a dislocation was calculated numerically by NEMBACH [16]. From the maximum and the range of this interaction force, the critical shear stress was also derived. Recently, FANG et al [17] investigated the interaction of dislocations and nanoscale cylindrical inclusions with interface stresses and its contribution to the critical shear stress of materials.

In this work, using the complex potential of the interaction between a screw dislocation and a core-shell nanowire with interface stress, the interaction energy and  the interaction force for this interaction were computed. The contribution to the critical shear stress of the composite materials owing to this interaction was derived by means of the obtained interaction force acting on the dislocation and MOTT and NABARRO’s model [18]. The effect of interface stress on the critical shear stress was examined.

2 Solution of critical shear stress

The basic model of the current problem is that an infinite medium (matrix phase) contains a circular nanowire and an annular nanoscale coating layer [19]. A screw dislocation b_z, which is assumed to be straight and infinite along the direction perpendicular to xy-plane and suffers a finite discontinuity in the displacement across the slip plane, is located at arbitrary points z₀ in the matrix phase. The nanowire is straight and infinitely extended in a direction perpendicular to xy-plane. The interface stresses are considered at the inner and outer interfaces of the coating layer.

For the current problem, the boundary conditions at the interfaces can be summarized as [19]

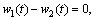
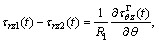
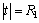                ₍₁₎

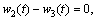
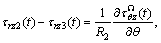
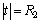              (2)

where w refers to the antiplane displacement; τ_rz and τ_θz are stress components in polar coordinates r and θ, respectively; R₁ and R₂ are the inner and outer radii of the coating annulus, respectively. Superscripts of Γ and Ω denote the inner and outer interfaces of the nanoscale coating layer, and subscripts 1, 2 and 3 refer to the nanowire, the nanoscale coating layer and the matrix regions, respectively; and t denotes the points on the interfaces. In addition, additional constitutive equations for the two interfaces are given as:

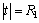                (3)

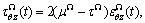
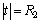               (4)

where  and 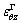  denote interfacial stress and strain, respectively; μ^Γ and μ^Ω are the interfacial elastic constants; and τ^Γ and τ^Ω are the residual interface tension. For a coherent interface, interfacial strains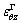and 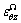are equal to the associated tangential strains in the abutting bulk materials.

Referring to Ref.[20], in the bulk solid, shear stresses τ_rz and τ_θz can be rewritten in terms of an analytical function Φ(z) of the complex variable z=x+iy as follows:

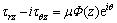                          (5)

where μ is the shear modulus of the material.

For the present problem, using Riemann-Schwarz’s symmetry principle integrated with Laurent series expansion technique [20], one obtains the analytical function Φ(z) in the matrix region:

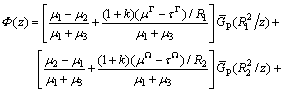
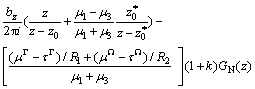        (6)

where μ₁, μ₂ and μ₃ are the shear moduli of the nanowire, coating layer and matrix phase, respectively; and  

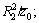
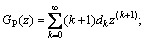
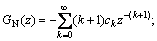
with

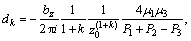
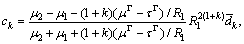
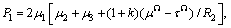
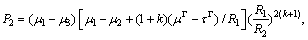
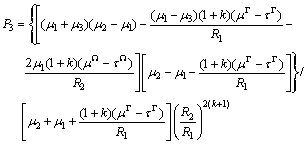
The components of the stress fields in the matrix can be derived from Eqs.(5) and (6).

The interaction energy can be formally written as

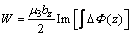                       (7)

where “Im” expresses the imaginary part of a complex quantity, “Δ” represents the part of the complex potential after the dislocation singularity is removed and Φ(z) is given by Eq.(6). The expression of ΔΦ(z) can be given as follows:

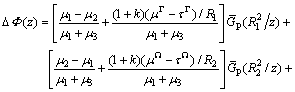
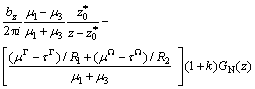
                                                                                                    (8)

The interaction energy for a screw dislocation at the point 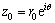can be found:

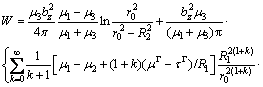
                                                                                                    (9)

The force acting on the screw dislocation is defined as the negative gradient of the interaction energy with respect to the position of the dislocation. Force f_r in polar coordinates is derived

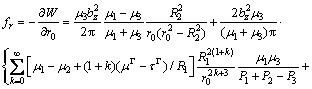
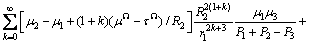
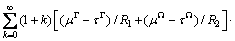
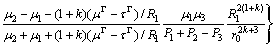 (10)

According to the idea of Ref.[18], consider the composites containing N core-shell nanowires per unit area, each of radius R₂. The average distance of the screw dislocation in the matrix from the nearest of them is half the distance between nanowires or r₀=N^-1/2/2. Thus, if 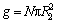 is the volume fraction of nanowires, the mean force f_rm acting on the screw dislocation can be obtained

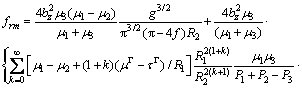
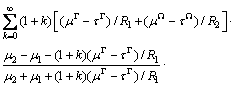
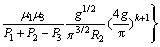                       (11)

Thus, the contribution to the critical shear stress ?τ_c caused by this elastic interaction can be derived from mean force f_rm (by NEMBACH [14]).

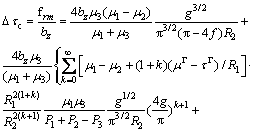
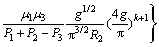                 (12)

The effect of the radius of the core-shell nanowire and the volume fraction of nanowires g as well as the interface stresses upon the critical shear stress can be studied according to Eq.(12).

3 Results and discussion

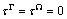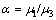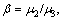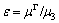In subsequent numerical calculation we suppose that the residual interface tension vanishes () and b_z=0.25 mm. In addition, one defines the relative shear moduli  and the relative coating thickness  and the intrinsic lengths  and 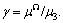 According to results in Ref.[21], the absolute values of the intrinsic lengths  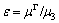and 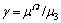are nearly 0.1 nm. The normalized critical shear stress ?τ₀ is defined as ×

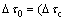The normalized critical shear stress Δτ₀ is plotted as a function of radius R₁ in Fig.1 with different interface properties for λ=0.6, the volume fraction of the core-shell nanowires g=0.1 and the relative shear moduli 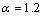 and It can be found that the contribution to the critical shear stress will increase with the reduction of the inhomogeneity radius R₁ without considering interface stresses, which is in agreement with the result in Ref.[13]. When the intrinsic length 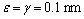[21] the critical shear stress also increases with the reduction of the inhomogeneity radius. However, if 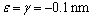[21], the contribution to the critical shear stress first increases and then decreases with the reduction of the inhomogeneity radius R₁. In this case, there is a critical value of the nanowires radius R₁ to determine the maximal contribution to the critical shear stress of the material when the volume fraction of the nanowire keeps a constant. The case cannot be predicted by the classical solutions without considering the interface effects [11].

Fig.1 Normalized critical shear stress Δτ₀ as function of R₁ at g=0.1,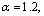 and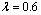

The variation of the normalized critical shear stress 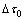with respect to the volume fraction g is depicted in Fig.2 with different interface properties for R₁=10 nm, λ=0.6 and the relative shear moduli  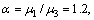and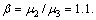 The results indicate that the contribution to the critical shear stress will increase with the increment of the volume fraction g when interface elastic constants are positive (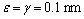). A special result in Fig.2 is that the critical shear stress will first increase and then decrease with the increment of the volume fraction g if 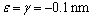[21] and the radius of the nanowire keeps a constant. There also exists a critical volume fraction g to obtain the maximal contribution to the critical shear stress of the material.

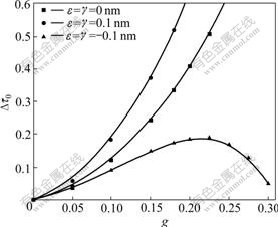
Fig.2 Normalized critical shear stress Δτ₀ as function of g at R₁=10 nm, 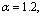and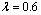

The normalized critical shear stress Δτ₀ is plotted as a function of radius R₁ in Fig.3 with different interface properties and the relative shear moduli  and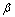(λ=0.6 and g=0.1). If the interface elastic constants are negative (ε=γ=-0.15 nm) [21] and the nanowire and the coating layer are all stiffer than the matrix, the contribution to the critical shear stress is positive first, and then becomes negative with the decrease of the inhomogeneity radius R₁. The results indicate the material may be softened by the stiff core-shell nanowires when the radius of the nanowire is very small and the interface effects are considered. Similarly, if the interface elastic constants are positive (ε=γ=0.15 nm) [21] and the nanowire and the coating layer are all softer than the matrix, the contribution to the critical shear stress is negative first, and then becomes positive with the decrease of the inhomogeneity radius R₁, which also shows that the material can be strengthened by the soft core-shell nanowires under certain conditions.

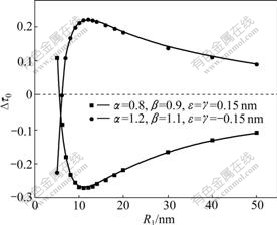
Fig.3 Normalized critical shear stress Δτ₀ as function of R₁ at g=0.1 and λ=0.6

In the following, the case of the composites containing the nanoholes with surface coatings (μ₁=0 or α=0) was discussed. Fig.4 illustrates the normalized critical shear stress Δτ₀ versus β=μ₂/μ₃ with different interface properties at R₁=10 nm, λ=0.6 and g=0.1. If the shear modulus of the coating layer is not variable, the strengthening or softening effect of the nanoholes with surface coatings will be more significant due to the existence of the interface stresses. There exists a critical shear modulus of the coating layer to change the strengthening effect or softening effect of the nanoholes. Fig.5 shows the normalized critical shear stress Δτ₀ versus the relative coating thickness λ with different interface properties at R₁=10 nm, β=3 and g=0.1. The influence of the interface stresses on the critical shear stress increases with the decrease of the relative thickness of the coating layer. If the shear modulus of the coating layer is fixed, there also exists a critical thickness of the coating layer to alter the strengthening effect or toughening effect produced by the nanoholes with surface coatings.

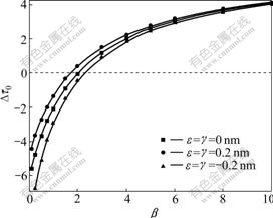
Fig.4 Normalized critical shear stress Δτ₀ as function of β for R₁=10 nm, g=0.1 and λ=0.6

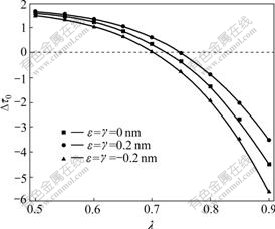
Fig.5 Normalized critical shear stress Δτ₀ as function of λ for R₁=10 nm, g=0.1 and β=3

4 Conclusions

(1) If the volume fraction of the core-shell nanowires is a constant and the interface stresses are considered, there is a critical value of the nanowire radius to determine the maximal critical shear stress of the material under some conditions in nanocomposites.

(2) If the radius of the nanowires keeps a constant, there exists a critical volume fraction to determine the maximal contribution to the critical shear stress caused by the interaction of dislocations with inhomogeneities.

(3) The material may be toughened by the stiff core-shell nanowires and strengthened by the soft nanowires when the interface stresses are considered.

(4) There exist critical values of the elastic modulus and the thickness of the coating layer (surface coating) to alter the strengthening effect or toughening effect produced by the surface coating.

References

[1] WEGROWE J E, SALLIN A, FABIAN A, COMMENT A, BONARD J M, ANSERMET J P. Magnetoresistance properties of granular nanowires composed of carbon nanoparticles embedded in a Co matrix [J]. Physical Review B, 2001, 65(1): 012407-6.

[2] ZHANG Xin-ming, YE Ling-ying, LIU Ying-wei, DU Yu-xuan, LUO Zhi-hui. Formation mechanism of gradient-distributed particles and their effects on grain structure in 01420 Al-Li alloy [J]. Journal of Central South University of Technology, 2008, 15(2): 147-152.

[3] WEN B, SADER J E, BOLAND J J. Mechanical properties of ZnO nanowires [J]. Physical Review Letters, 2008, 101(17): 175502-1- 175502-3.

[4] TSUCHIDA E, OHNO M, KOURIS D A. Effects of an inhomogeneous elliptical insert on the elastic field of an edge dislocation [J]. Applied Physics A, 1991, 53(4): 285-291.

[5] XIAO Z M, CHEN B J. A screw dislocation interacting with a coated fiber [J]. Mechanics of Materials, 2000, 32(8): 485-494.

[6] FANG Qi-hong, LIU You-wen. Size-dependent interaction between an edge dislocation and a nanoscale inhomogeneity with interface effects [J]. Acta Materialia, 2006, 54(16): 4213-4220.

[7] TAKAHASHI A, GHONIEM N M. A computational method for dislocation–precipitate interaction [J]. Journal of the Mechanics and Physics of Solids, 2008, 56(4): 1534-1553.

[8] FANG Qi-hong, LIU You-wen, CHEN Jiang-hua. Misfit dislocation dipoles and critical parameters of buried strained nanoscale inhomogeneity [J]. Applied Physics Letters, 2008, 92(12): 121923-3.

[9] FANG Qi-hong, LIU You-wen, JIN Bo, WEN Pi-hua. Effect of interface stresses on the image force and stability of an edge dislocation inside a nanoscale cylindrical inclusion [J]. International Journal of Solids and Structures, 2009, 46(6): 1413-1422.

[10] DAVOUDI K M, GUTKIN M Y, SHODJA H M. A screw dislocation near a circular nano-inhomogeneity in gradient elasticity [J]. International Journal of Solids and Structures, 2010, 47(3): 741-750.

[11] BRANDS M, CARL A, POSTH O, DUMPICH G. Electron-electron interaction in carbon-coated ferromagnetic nanowires [J]. Physical Review B, 2005, 72(8): 085457-8.

[12] MARTIN C R, SIWY Z. Molecular filters: Pores within pores [J]. Nature Materials, 2004, 3(1): 284-285.

[13] DUAN H L, WANG J, KARHALOO B L, HUANG Z P. Nanoporous materials can be made stiffer than non-porous counterparts by surface modification [J]. Acta Materialia, 2006, 54(11): 2983-2990.

[14] NEMBACH E. Particle strengthening of metals and alloys [M]. New York: Wiley, 1996: 153-162.

[15] RUSSELL K C, BROWN L M. A dispersion strengthening model based on different elastic moduli applied to the Fe-Cu system [J]. Acta Metallurgica, 1972, 20(2): 969-974.

[16] NEMBACH E. Precipitation hardening caused by a difference in shear modulus between particle and matrix [J]. Physica Status Solidi A, 1983, 78(2): 571-581.

[17] FANG Qi-hong, LIU Yong, HUANG Bo-yun, LIU You-wen, WEN Pi-hua. Contribution to critical shear stress of nanocomposites produced by interaction of screw dislocation with nanoscale inclusion [J]. Materials Letters, 2008, 62(20): 3521-3523.

[18] MEI Q S, LU K. Melting and superheating of crystalline solids: Form bulk to nanocrystals [J]. Progress in Materials Science, 2007, 52(8): 1175-1262.

[19] FANG Qi-hong, LIU You-wen, JIN Bo, WEN Pi-hua. Interaction between a dislocation and a core-shell nanowire with interface effects [J]. International Journal of Solids and Structures, 2009, 47(6): 1539-1546.

[20] MUSKHELISHVILI N L. Some basic problems of mathematical theory of elasticity [M]. Leyden: Noordhoff, 1975: 223-227.

[21] MILLER R E, SHENOY V B. Size-dependent elastic properties of nanosize structural elements [J]. Nanotechnology, 2000, 11(3): 139-147.

Foundation item: Projects(50801025, 50634060 ) supported by the National Natural Science Foundation of China

Received date: 2009-07-02; Accepted date: 2009-10-16

Corresponding author: FANG Qi-hong, PhD, Associate professor; Tel: +86-731-88823517; E-mail: fangqh1327@tom.com

(Edited by YANG You-ping)