文章编号：1004-0609(2007)10-1678-07

AZ80镁合金的高温热压缩变形行为

栾  娜¹，李落星¹，李光耀²，钟志华²

(1. 湖南大学 材料科学与工程学院，长沙 410082；

2. 湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082)

摘  要：在应变速率为0.01~50 s^-1、温度为300~450 ℃的条件下，在Gleeble-3500热模拟机上对AZ80镁合金的高温热压缩变形特性进行研究。实验得出变形过程中的真应力应变曲线，并利用本构方程对流变应力值进行修正，进而利用修正后的应力值得出本实验本构方程中的系列常量；实验还分析温度、应变速率及应变量对微观组织的影响。结果表明：变形过程中的应力值随温度的升高而降低，随应变速率的升高而升高，且修正后的应力值高于未修正值；变形过程中发生动态再结晶且晶粒平均尺寸随变形参数的不同而改变，其自然对数随Zener-Hollomon(Z)参数的自然对数的升高呈线性降低。

关键词：AZ80镁合金；热变形；流变应力；本构方程

中图分类号：TG 146.2　　     文献标识码：A

Hot compression deformation behaviors of AZ80 magnesium alloy at elevated temperature

LUAN Na¹, LI Luo-xing¹, LI Guang-yao², ZHONG Zhi-hua²

(1. College of Materials Science and Engineering, Hunan University, Changsha 410082, China;

2. State Key Laboratory of Advanced Design and Manufacture for Vehicle Body, Hunan University,

Changsha 410082, China)

Abstract: Hot compression tests of AZ80 magnesium alloy were performed on Gleeble-3500 at strain rates ranged in 0.01-50 s^-1 and deformation temperature ranged in 300-350 ℃. The true stress/true strain curves were obtained in the tests. The flow stress was corrected by the constitutive equations and the constants in the constitutive equations were calculated using the corrected stress. The relation between stress and strain is obviously affected by strain rate and deformation temperature. The results show that the flow stress increases with the increase of strain rate at constant temperature, and decreases with the increase of deformation temperature at constant strain rate. The corrected flow stress is generally higher than the uncorrected value. The dynamic recrystallization takes place during the deformation process, and the average dynamically recrystallized grain size changes with deformation variables. A linear relationship between ln Z and ln d_r is obtained (Z is Zener-Hollomon parameter and d_r is average grain size).

Key words: AZ80 magnesium alloy; hot compression deformation; flow stress; constitutive equation

镁合金由于密度小，比强度、比刚度高，尺寸稳定性和热导率高，机械加工性能好，产品易回收利用，成为21世纪重要的商用轻质结构材料^[1]。目前，工业发达国家已大力着手高性能变形镁合金加工型材的研究与开发^[2-7]。由于镁和多数镁合金属密排六方结构，室温滑移系较少，塑性较差，成形困难，因此通常情况下只能通过热加工来生产变形镁合金产品。

为了研究材料热变形行为，材料在高温下的流变应力是不可缺少的变量之一。流变应力是表征金属和合金变形性能的一个基本量，而且在变形过程的数值分析中起着重要的作用。在热变形过程中，流变应力行为一般受变形温度、应变速率、应变量等参数的影响。Takuda等^[8]描述了AZ31和AZ91镁合金热变形时的流变应力，用Z参数的形式简单表述了Z参数与流变应力的关系；日本大阪府立大学东健司研究小组^[9]对Mg-Al-Zn系合金(AZ31和 AZ61)晶粒尺寸大小受动态再结晶控制关系进行研究，建立了用来预测热变形过程中动态再结晶晶粒尺寸大小的本构方程；汪凌云等^[10]对AZ31镁合金的研究发现在热压缩变形过程中，动态再结晶平均晶粒尺寸(d)的自然对数与Zener-Hollomon参数的对数呈线性关系。因此研究镁合金在热加工过程中的变形特性具有很重要的理论意义和应用价值^[11]。

本文作者在变形温度为300~450 ℃和应变速率为0.01~1 s^-1条件下，通过对AZ80镁合金进行高温压缩变形的实验研究，充分考虑变形热对变形过程中试样温度的影响，利用变形本构方程对流变应力值进行修正，并利用修正的流变应力值来确定合金变形本构方程中的材料常量。还通过对变形后试样组织结构的观测，研究AZ80镁合金高温压缩变形过程的组织演变规律，探讨变形过程中Z参数与再结晶晶粒平均尺寸之间的关系，为合理制定AZ80镁合金热塑性加工工艺参数提供指导，并可为变形过程的数值模拟^[12-13]提供数据基础。

1  实验

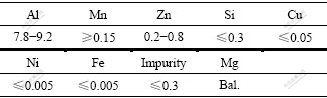
实验使用的材料是直径为47.2 mm的AZ80镁合金热挤压棒。表1所列为AZ80镁合金的化学成分。沿垂直挤压方向截取直径为10 mm，高为12 mm的圆柱体试样，在Gleeble 3500热模拟实验机上进行热压缩实验，试样的初始温度分别为300、350、400和450 ℃，应变速率分别为0.01、0.1、1、10和50 s^-1。压缩前，石墨薄片作为润滑剂放在样品和压头间，以减小试样与压头之间的摩擦影响。通过一热电偶对将样品在变形过程中的温度变化记录下来，所采用的热电偶直径为0.08 mm，测量的反应时间为0.1 s。样品以10 ℃/s的速率加热到预设温度，保温60 s以保证温度的均匀化，然后压缩到高度4.4 mm，即到达真应变1。整个实验都在氮气氛下进行。另外，合金的显微组织采用LeitZ公司MM-6卧式金相显微镜进行观察。

表1  AZ80镁合金的化学成分

Table 1  Chemical composition of alloys (mass fraction, %)

2  AZ80镁合金在热压缩过程中的力学行为

2.1  应力应变曲线

AZ80镁合金在不同变形条件下真应力σ同真应变ε的关系曲线如图1所示。

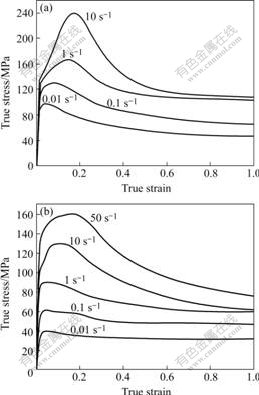
图1  AZ80镁合金真应力—真应变关系曲线

Fig.1  Curves of true stress—true strain at different temperatures and strain rates: (a) 300 ℃; (b) 400 ℃

从图1可以看出，AZ80镁合金热压缩变形时流变应力的总体变化规律表现为：变形初期，流变应力随真应变的增加迅速上升；在高温低应变速率下(图1中400 ℃、0.01 s^-1)，流变应力出现一峰值后表现为流变软化的特征而逐渐下降，直到基本保持恒定，这时加工硬化与流变软化达到平衡，应力应变曲线平衡；在低温高应变速率下(如图1中300 ℃、10 s^-1)，出现一峰值后，应力—应变曲线一直呈下降的趋势，流变软化特征更为明显。另外，随着应变速率的增大和温度的降低，进入稳态变形时对应的真应变值增大。

2.2  变形热对流变应力的影响

流变软化是许多合金在高温变形过程中应力应变曲线最普通的特征。它是由变形热即温升或材料内部微结构的不稳定性引起的。在经验或半经验本构方程中，只考虑了变形热，而未考虑微结构的不稳定性所引起的软化作用。所以本研究中，只讨论温度的升高对流变软化的影响。由于变形过程中，测量温度的电偶对的反应时间是0.1 s，所以该电偶对只能测量变形时间＞0.1 s(即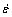＜10 s^-1)的变形过程，而对于变形时间≤0.1 s(即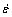≥10 s^-1)变形过程，其测量值是不真实的。针对上述情况，本文作者引入以下方程^[14]计算高应变速率下由变形热所引起的试样温升。用初始温度加上该温升就是变形过程中实际的温度。

式(1)中，在低应变速率时的等热条件下η取0，而在高应变速率时的绝热条件下η取1，因子0.9~0.95是由机械功转变为热量的分数。在高应变速率下，变形时间短，合金在短时间内所产生的大量的热来不及散失，使合金内部温度急剧上升，该状态可近视绝热的环境。因此在本研究中，高应变速率下(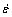≥10 s^-1)，η取为1，并设定变形过程中90％的机械功转变为热量^[15]。根据式(1)可计算出各个温度、应变速率和应变条件下对应的试样温升ΔT，再加上实验的初始温度即为修正后试样的实际温度值。图2所示为变形过程中试样温度的测量值(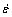≤1 s^-1)和计算值(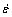≥10 s^-1)。从图中可以看出，在低应变速率下，试样温度在整个变形过程中基本维持不变，而高应变速率下试样温度呈持续上升状态。

3  本构方程的建立及流变应力的修正

根据以上所得到的测量温度和计算温度，建立AZ80镁合金高温热压缩过程中的本构方程，并结合变形热来修正流变应力。研究表明，用来描述金属材料高温变形的流变应力主要取决于应变ε、温度T和应变速率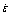，通常用以下公式来表示流变应力的本构模型^[16]：

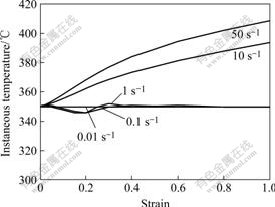
图2  预设温度350 ℃时各应变速率下的瞬时温度

Fig.2  Relationships between strain and instantaneous temperature at different strain rates and pre-set temperature of 350 ℃

式(4)中的α是可调常量，恒温时，当ln[sinh(ασ)]与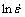曲线趋于线性并相互平行时，可得到α的最优值。在本研究中，计算α的最优值时，不能采用测量的应力值，因为在压缩过程中，特别是在高应变速率下，试样温度在不断变化，不能得出恒温条件下的应力—应变曲线，所以应先用式(6)和式(7)对流变应力进行修正。从图2可以看出，高应变速率下试样温升明显，而低应变速率下试样温度基本维持恒定，所以本研究只对高应变速率下的流变应力进行修正，具体修正方法见文献[15]。

图3所示为高应变速率下修正的应力应变曲线与未修正的应力应变曲线的对比曲线。从图3可以看出，修正与未修正曲线的走向一致，且在低应变下，两曲线基本重合，但到达峰值应力后，修正曲线就明显高于未修正曲线。当温度为400 ℃、应变速率为10 s^-1、应变达到1时，修正与未修正应力差值达最大为31.38 MPa。另外，从图3还可以看出，即使引入了变形热的修正，流变曲线仍然表现出流变软化的特征，相关机理有待进一步研究。

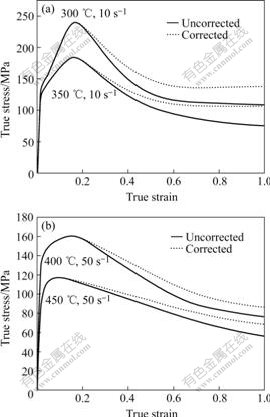
图3  修正与未修正曲线对比

Fig.3  Comparison between corrected and uncorrected true stress—true strain curves: (a) 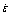=10 s^-1; (b) 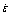=10 s^-1

将修正的应力值应用于式(9)可计算出一定温度、一定应变速率和各应变量下的激活能Q及其它材料参数，见表2。从表2可以看出，α和ln A随不同的测量参量而有所不同。n、S、Q在峰值应力后即应变为0.4时逐渐达到一稳定值，表明变形达到了一个稳定状态。

表2  各个应变下用修正应力所获得的本构常量

Table 2  Constitutive constants obtained from corrected flow stresses at selected strains

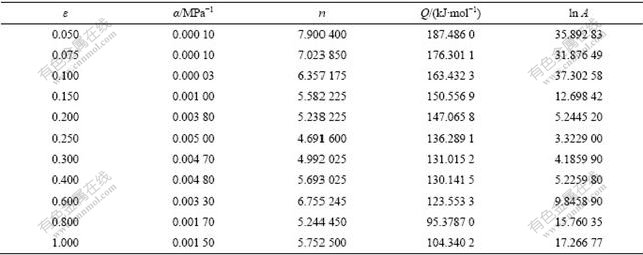
将这些材料常数代入式(5)中，即可求得材料在任何变形条件下流变应力的大小。

4  AZ80镁合金高温变形显微组织分析

4.1  变形工艺参数对显微组织的影响

图4所示为温度为300 ℃、应变速率为10 s^-1、在不同应变(0、0.2、0.5、1)时合金的金相组织。从图中可以看出，AZ80镁合金在温度300 ℃、应变速率10 s^-1变形时发生了动态再结晶^[18]。随着变形量的增加，动态再结晶晶粒的组分逐渐增加，晶粒尺寸得到显著细化，更加均匀。图4(a)所示为AZ80镁合金的原始组织；图4(b)中的应变量为0.2，晶界呈锯齿状，再结晶晶粒开始沿着晶界和晶界三角连接处形核，细晶粒的体积比例约为53%，其余为变形前的未再结晶组织，此时为不完全再结晶，晶粒平均尺寸约32.49 μm；当应变量为0.5时(图4(c))，细小再结晶晶粒的比例已增加到82%，这是因为动态再结晶开始于旧晶界处，新的晶粒又可在正在长大的再结晶晶粒边界形核长大^[19]，导致其整体平均晶粒尺寸约为22.14 μm；当应变量达到1时(图4(d))，微观形貌图中原始粗大晶粒已基本不存在，几乎全为细晶粒的再结晶组织，晶粒组织得到充分细化，平均晶粒尺寸约为14.51 μm，且趋于均匀。

图4  AZ80镁合金在300 ℃、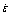=10 s^-1和不同变形量下的显微组织

Fig.4  Microstructures of AZ80 magnesium alloy at 300 ℃, 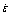=10 s^-1 and different strains: (a) ε=0; (b) ε=0.2; (c) ε=0.5; (d) ε=1

图5所示为温度为450 ℃，应变速率为10 s^-1、应变量为1时AZ80镁合金的金相组织，对比图4(d)可以发现，随着变形温度的升高，动态再结晶晶粒尺寸明显增大，晶粒的平均尺寸为33.52 μm左右。

图5  AZ80 镁合金在450 ℃、=10 s^-1和ε=1时的显微组织

Fig.5  Microstructure of AZ80 magnesium alloy at 300 ℃, =10 s^-1 and ε=1

图6所示为温度为450 ℃，应变量为1时，在不同应变速率(0.01 s^-1，50 s^-1)时合金的金相组织。从图中可以看出，在应变速率较低的情况下变形(图6(a))，晶粒较粗大，且大小很不均匀；随着变形速率的增加，再结晶晶粒越来越细小且比较均匀，如图6(b)所示。由于镁合金是低层错能金属，动态再结晶是热变时的典型机制。而动态再结晶的驱动力一般是由变形金属的储存能提供。当应变速率较低时，金属原子可充分扩散，合金中的储存能较少，使得再结晶驱动力减少，因而只能在某些具有高能量起伏的区域(如变形量大的区域)首先形核，再结晶形核率较低；而当变形速率较高时，产生同样变形程度所需的时间短，导致部分区域位错来不及抵消和合并，位错增多，再结晶形核位置多，导致晶粒细化。另外，由于在高应变速率下，变形时间较短，再结晶晶粒来不及长大，所以随应变速率的增大，晶粒得到细化。

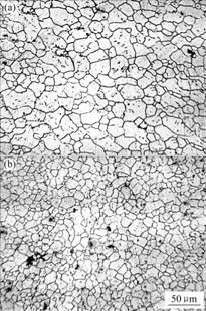
图6  AZ80镁合金在450 ℃、ε=1和不同应变速率下的显微组织

Fig.6   Microstructures of AZ80 magnesium alloy at  450 ℃, ε=1 and different strain rates: (a) 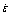=0.01 s^-1; (b) 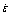=50 s^-1

4.2  Z参数与晶粒尺寸之间的关系

由4.1节分析可知，AZ80镁合金高温热压缩变形微观组织不仅与温度有关，还与应变速率有关。Zener-Hollomon参数综合了温度和应变速率对材料组织的影响，因此引入Z参数可以分析AZ80镁合金热变形过程中晶粒尺寸的变化。Z值与变形温度和应变速率的关系如下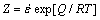：。另外，有研究 ^[20]表明：热变形时再结晶晶粒的平均直径d_r与Z参数存在如下关系：

在本实验中，AZ80镁合金热压缩变形应变量为1时再结晶晶粒的平均尺寸d_r与Z参数的关系如图7所示。

由图7可知，ln d_r与ln Z呈线性关系，且随着Z值的增大，再结晶晶粒尺寸d_r减小。也就是说，降低变形温度和提高应变速率都可以减小再结晶晶粒尺寸。但在生产实际中，变形温度降低和应变速率升高都会降低材料的可成形性，同时所需的变形力增加。因此制定AZ80镁合金热压缩变形工艺时，要获得细晶组织，必须采用适宜的变形温度和变形速度，同时还要考虑材料的可成形性以及设备能力。

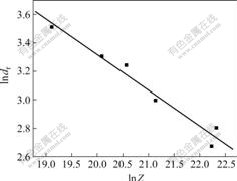
图7  ln d_r与ln Z的关系

Fig.7  Relationship between Zener-Hollomon parameter and grain size of recrystallization

5  结论

1) AZ80镁合金高温热压缩变形过程中，流变应力随变形温度的升高和应变速率的降低而减小。高应变速率下，由于试样温升的影响，实验记录的流变应力曲线为非恒温条件下的结果，对高应变速率下流变应力修正的结果显示，修正后的流变应力大于实际记录值。

2) AZ80镁合金在高温压缩变形过程中发生动态再结晶，随着应变速率的升高和变形温度的降低，再结晶过程更完全。如果用Z参数来归纳温度和应变速率对再结晶过程的影响，AZ80镁合金热压缩过程中再结晶晶粒的平均尺寸d_r随Z值的增大而减小，且   ln d_r与ln Z呈线性关系，即ln d_r=-0.25ln Z+8.337。另外，随压缩变形量的增加，AZ80镁合金的动态再结晶分数增大。

REFERENCES

[1] Decker R F. The renaissance in magnesium[J]. Adv Mater Process, 1998, 154(3): 31-33.

[2] Froes F H, Eliezer D, Aghion E. The science, technology and applications of magnesium[J]. JOM, 1998, 9: 30-33.

[3] Clow B B. Magnesium industry overview[J]. Adv Mater Process, 1996, 10: 33-36.

[4] Mordike B L, Ebert T. Magnesium properties-applications- potential[J]. Mater Sci Eng A, 2001, A302: 37-45.

[5] Polmear I J. Magnesium alloys and applications[J]. Mater Sci Tech, 1994, 10: 1-16.

[6] Friedrich H, Schumann S. Research for a “new age of magnesium” in the automotive industry[J]. Mater Process Tech, 2002, 117(3): 276-281.

[7] Aghion E, Bronfin B, Eliezer D. The role of the magnesium industry in protecting the environment[J]. Mater Process Tech, 2001, 117(3): 381-385.

[8] Takuda H, Fujimoto H, Hatta N. Modelling on flow stress of Mg-Al-Zn alloys at elevated temperatures[J]. Mater Process Tech, 1998, 80/81: 513-516.

[9] Mabuchi M, Tsatui H, Iwasaki H. Low temperature superplasticity of AZ91 magnesium alloy[J]. Acta Mater, 1999, 47(7): 2047-2057.

[10] 汪凌云，黄广胜，范永革，黄光杰. 变形AZ31镁合金的晶粒细化[J]. 中国有色金属学报, 2003, 13(3): 594-598.
WANG Ling-yun, HUANG Guang-sheng, FAN Yong-ge, HUANG Guang-jie. Grain refinement of wrought AZ31 magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2003, 13(3): 594-598.

[11] 郭 强, 严红革, 陈振华, 张 辉. AZ31镁合金高温热压缩变形特性[J]. 中国有色金属学报, 2005, 15(6): 900-906.
GUO Qiang, YAN Hong-ge, CHEN Zhen-hua, ZHANG Hui. Hot compression deformation behavior of AZ31 magnesium alloy at elevated temperature[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(6): 900-906.

[12] Zhou J, Li L, Duszczyk J. Computer simulated and experimentally verified isothermal extrusion of 7075 aluminium through continuous ram speed variation[J]. Mater Process Tech, 2004, 146(2): 203-212.

[13] Zhou J, Li L, Duszczyk J. 3D FEM simulation of the whole cycle of aluminium extrusion throughout the transient state and the steady state using the updated Langranian approach[J]. Mater Process Tech, 2003, 134(3): 383-397.

[14] Goetz R L, Semiatin S L. The adiabatic correction factor for deformation heating during the uniaxial compression test[J]. Journal of Materials Engineering and Performance, 2001, 10(6): 710-717.

[15] Li L, Zhou J, Duszczyk J. Determination of a constitutive relationship for AZ31B magnesium and validation through comparison between simulated and real extrusion[J]. Mater Process Tech, 2006, 172(3): 372-380.

[16] McQueen H J, Belling J. Constitutive constants for hot working of Al-4.5Mg-0.35Mn(AA5182)[J]. Canadian Metallurgical Quarterly, 2000, 39(4): 486-492.

[17] McQueen H J, Ryan N D. Constitutive analysis in hot working[J]. Mater Sci Eng A, 2002, 322(1/2): 43-63.

[18] 刘楚明, 刘子娟, 朱秀荣, 周海涛. 镁及镁合金动态再结晶研究进展[J]. 中国有色金属学报, 2006, 16(1): 1-12.
LIU Chu-ming, LIU Zi-juan, ZHU Xiu-rong, ZHOU Hai-tao. Research and development progress of dynamic recrystallization in pure magnesium and its alloys[J]. The Chinese Journal of Nonferrous Metals, 2006, 16(1): 1-12.

[19] Cahn R W. 材料科学与技术丛书(15卷): 金属与合金工艺[M]. 雷廷权译. 北京: 科学出版社, 1999.
Cahn R W. Series of materials science and technology (Vol 15): Metal and alloy process[M]. Lei Ting-quan transl. Beijing: Science Press, 1999.

[20] Watanabe H, Tsutsui H, Mukai T, Ishikawa K, Okanda Y, Kohzu M, Higashi K. Grain size control of commercial wrought Mg-Al-Zn alloys utilizing dynamic recrystallization[J]. Mater Trans, 2001, 42(7): 1200-1205.

基金项目：教育部新世纪优秀人才资助计划项目(20062148183)

收稿日期：2007-05-22；修订日期：2007-06-11

通讯作者：李落星，教授；电话：0731-8821610；E-mail: luoxing_li@yahoo.com

(编辑 何学锋)