J. Cent. South Univ. (2016) 23: 1535-1540
DOI: 10.1007/s11771-016-3205-y

Equilibrium analysis of mixed passengers in urban railway network
ZHANG Lu(张璐)1, WU Jian-jun(吴建军)1, SUN Hui-jun(孙会君)2
1. State Key Laboratory of Rail Traffic Control and Safety (Beijing Jiaotong University), Beijing 100044, China;
2. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: A model is proposed to describe the passengers’ route choice behaviors in urban railway traffic with stochastic link capacity degradation by considering two types of demand, sensitive and insensitive passenger. The insensitive passengers choose their route without paying much attention to congestion. To the contrary, sensitive passengers who consider route congestion choose travel route based on generalized cost. An equilibrium state is given by variational inequalities in terms of travel generalized cost, which is represented by the combinations of mean and variance of total travel time. The diagonalization algorithm is given to solve this programming. Results show that insensitive passengers have large effects on the path choice than sensitive ones, especially for the larger demand.
Key words: mixed passengers; urban railway network; capacity degradation; equilibrium
1 Introduction
Urban railway systems can provide rapid transport, massive transportation volumes, high reliability, safety service etc., which are a main part of modern urban traffic networks. All makes it have been regarded as the most efficient method to alleviate the urban traffic congestion. It plays an important role in analyzing the passenger flow distribution so as to plan the capacity in the urban railway network (URN). Recently, a number of studies have been devoted to the passenger flow assignment problem in the transit network [1]. Most of methods are based on the well-developed traffic flow assignment model in the road network which includes divided two parts. One is under the determinist condition where the capacity and the demand are perfectly known. The other is to think that both supply and demand are subject to stochastic variations. As we all know, URN is a complex system and does not always work as expected because of uncertain input parameters or unforeseen events which are subject to stochastic variations in reality. Even for minor events, such as vehicle breakdown and congestion, they can influence the flow distribution and the whole system. Therefore, the study on flow assignments based on stochastic characteristics in the urban railway network is more realistic and becomes a hotspot for researches gradually.
In fact, stochastic user equilibrium (SUE) assignment has been widely used in the road traffic and is well known as a general model which consistently unifies the concept of the stochastic assignment and Wardropian equilibrium since it was proposed by DAGANZO and SHEFFI [2] and FISK [3]. It not only overcomes the shortcoming of the homogeneous user assumption in the Wardropian equilibrium, but also researches the random effect of the stochastic assignment problem on a congested road network [4]. NIELSEN [5] developed a stochastic transit assignment model considering differences in passengers’ utility functions. CLARK and WATLING [6] and SUMALEE et al [7] considered the effects of stochastic demand on network reliability. SZETO and LO [8] modeled commuters’ route choice behavior under stochastic link capacity degradation by the notion of “travel time budget”. SIU and LO [9] developed a methodology to model doubly uncertain transportation network with stochastic link capacity degradation and stochastic demand. SUN et al [10] proposed optimization models to design demand-driven timetables for a single-track metro service. The results show that demand-sensitive timetables have advantage in reducing waiting time and congestion.
In addition, faced with uncertainty about the travel cost in their route choice, passengers are required to make a trade-off between the travel cost and its uncertainty. This behavior is known as risk taking behavior [11]. Many studies [12-14] have been performed to model this risk-taking behavior of route choices. Choice behaviors of passengers with different risk aversions based on stochastic characteristics are analyzed in detail. NIKOLOVA and STIER-MOSES [15] proposed a new traffic assignment model that took into account the stochastic nature of travel times. The model extends the traditional model of Wardrop competition when uncertainty is present in the network. CANTARELLA et al [16] presented a general fixed- point approach that allowed dealing with multi-user stochastic equilibrium assignment with variable demand. JANG [17] presented an empirical study on identifying travel time and transfer pattern which provides meaningful information for passengers’ transfer choice. SUN and XU [18] introduced the stochastic cost of walking-in, waiting, transfer and walking-out. The approach characterizes the distribution of travel time and use mean and variance to estimate the weight parameter. ZHOU and XU [19] proposed a maximum likelihood estimation method of individual passenger route choice to establish a flow assignment model which was put forward to map the passenger flow. ZHU et al [20] presented a framework to calibrate passenger flow assignment model in metro networks based on genetic algorithm. SUN et al [21] proposed an integrated Bayesian statistical inference framework to characterize passenger flow assignment model in a complex metro network.
These settings are non-cooperative, and usually assume that such rational passengers are well- approximated by the selfish users of the models referred to above. But there is a different kind of passenger as well: these are the passengers who plan their routes ahead of time and are not sensitive to the congestion in the railway. Such passengers are oblivious to the traffic patterns of the other users, and therefore are not affected by congestion considerations. The natural question that arises is how the existence of a fraction of such oblivious users affects the passenger choice behaviors. The aim of this work is to investigate the flow distribution in the network with two kinds of passengers: passengers considering congestion effects will adjust their route based on traffic information, and in an equilibrium state, they choose the shortest route (sensitive passenger). Other passengers who are not sensitive to the congestion caused by the flow increase (Insensitive passenger) will choose their routes based on real time. We further discuss the capacity degradation effects on the behaviors of these two types of passengers. So, the study on mixed passengers based on stochastic conditions is significant for URN.
2 Network description
URN contains a lot of general stations and transfer stations where passengers can change the route line to destination, a lot of trains and lines. Generally, it can be represented by TNR=(S, R, O), where S, R and O respectively are the sets of stations, link and operation lines on the physical URN. In this work, the railway system is described by an augmented network, G=(N, E), where N is a set of augmented stations and E is a set of augmented links. In this section, the mathematical formulations of the urban railway traffic flow assignment models for a stochastic network with cost uncertainty are presented.
2.1 Link travel cost
In general, in-train time, waiting time, transfer time and delay time constitute link travel cost of passengers in URN. In-train cost includes the time spent in the train and the cost caused by crowded passengers. The former is dependent on the running time and the stop time of train, which can be represented by ta. However, the congestion effects can be described with uncomfortable function. Let coefficients A (general congestion) and B (overcrowding) be taken into account when applying the uncomfortable function [22]:
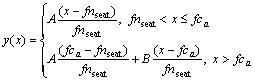 (1)
(1)
Therefore, the in-train time can be represented as
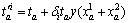 , i=1, 2 (2)
, i=1, 2 (2)
Waiting time is that passengers spend time waiting for train when they arrive at the station, which is related to the number of passengers on the platform and departure frequency of the train. It can be written as w=α/f. Many passengers take transfer time to change one line to another, which can be calculated by th=L/vh. The factors of the density of passenger, the walking speed of passenger and the length of transfer channel will affect transfer time. For the delay time, it is the extra time that passenger takes to wait for the following trains because of waiting passengers exceeding the maximum capacityof a train, which is similar to the BPR, 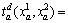
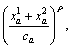 where ρ is the parameter. Generally, the link travel cost in URN is the sum of in-train time, waiting time, transfer time and delay time, which can be written as [22]
where ρ is the parameter. Generally, the link travel cost in URN is the sum of in-train time, waiting time, transfer time and delay time, which can be written as [22]

 i=1, 2 (3)
i=1, 2 (3)
2.2 Different choice behaviors
As the link capacity is subject to stochastic degradation, ca is replaced by the random variable Ca.Then, in Eq. (3), the link travel time becomes a random variable:
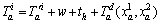 (4)
(4)
where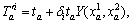

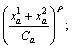 i=1, 2.
i=1, 2.
In addition, it is assumed that sensitive passengers know the traffic condition better and they choose the route based on the generalized link cost 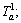 while for in sensitive passengers, they do not care about the congestion and have a lower sensitive parameter to congestion, so they will choose the route based on the following link cost
while for in sensitive passengers, they do not care about the congestion and have a lower sensitive parameter to congestion, so they will choose the route based on the following link cost 
Link capacity degradations and stochastic demand cause link and route travel time variability. Commuters, therefore, do not know their exact a priori travel times. Some commuters would depart earlier to allow for additional time, or add a travel time margin to the expected trip time, in order to avoid late arrivals [9]. In other words, commuters allow for a longer travel time budget to hedge against travel time variability. SZETO and LO [8] defined the travel time budget to study passengers’ route choice behaviors.
Passengers are assumed to choose the path that will minimize their expected travel time. This assumption represents the risk-neutral case. In this work, passengers are assumed to consider both the mean travel time and reliability in their route choice decision, which represents risk-based behaviors. Therefore, the generalized travel cost associated with link a is assumed to depend on both the mean and the variance of the travel time of that link, which is defined as
 i=1, 2 (5)
i=1, 2 (5)
where λ is the degree of risk aversion and represents the relative weight in mean and variance of travel time.
In this work, to simplify the exposition, it was assumed that link capacity follows a uniform distribution with the design capacity of the link as its upper bound and the worst degraded capacity as its lower bound. Furthermore, the lower bound is considered to be a fraction of the design capacity (θca, ca) [9]. Let TC=  The following equation can be derived.
The following equation can be derived.
When  ,
,
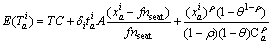 (6)
(6)
 (7)
(7)
When 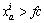 ,
,
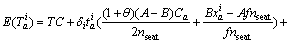
 (8)
(8)
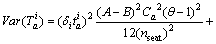
 (9)
(9)
3 Route choice model at equilibrium and solution algorithm
3.1 Augmented URN
To adopt the traditional traffic flow assignment method, the urban railway network should be augmented to a general graph where no transfer stations are included. In the augmented process, each transfer station can be separated into the augmented nodes and each augmented node belongs to one operation line. Then, the augmented nodes are connected to their two neighbor stations through the transit line. Besides, the corresponding augmented nodes should connect transfer links if different transit lines can be transferred in the same station.
There are some considerations when establishing the connectivity between the augmented stations through the transfer links. Transfer behavior between augmented nodes of a station should not happen, which is also forbidden between different lines at the stations that are connected with the origins or destinations. And there are no self-loop and multi-link in the augmented network. What's more, if two virtual stations belong to the same operation line, the cost (time) is zero. Otherwise, it is the transfer time.
3.2 Route choice model
In modeling route choices of passengers, the notion of a long-term habitual equilibrium is drawn. That is, after experimenting and exploring their route choices for an extended period of time, passengers settle into a set of fixed route choices day in and day out and they do not have incentive to switch away. Formally, this long-term habitual equilibrium route choice pattern is analogous to the Wardropian principle.
For each OD pair, the flow of type i passengers, 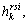 on route k is positive if the generalized travel cost on that route is equal and minimal; all unused routes have an equal or higher generalized travel cost. The generalized travel cost equilibrium conditions for them can be described by
on route k is positive if the generalized travel cost on that route is equal and minimal; all unused routes have an equal or higher generalized travel cost. The generalized travel cost equilibrium conditions for them can be described by
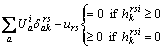 (10)
(10)
which can be represented with a variational inequalities:
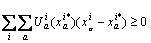 (11)
(11)
where 
 and
and 
3.3 Solution algorithm
There are lots of methods to solve the VI problem, such as the diagonalization method, the projection method, the alternating direction method and the decomposition method.
In this work, the model is solved in a diagonalization scheme, in which the solution of the sub-VI or minimization problem of each player can be obtained in an iterative and alternate manner. This algorithm models the iterative reaction of each player in the network based on the previous reaction of the other players, and the procedure continues until a steady state or convergence is achieved. This type of approach has been successfully applied by HARKER [23] and VAN et al [24]. In the sub-problems produced by the diagonalization method, the F-W method was used for solving the network equilibrium problem.
The diagonalization algorithm for the mixed equilibrium problem can be summarized as follows [25]:
Step 1 (Initialization): Compute the cost of the efficient shortest paths from the free flow cost  then compute the initial link flow
then compute the initial link flow  Set n=0.
Set n=0.
Step 2 (Diagonalization): Solve the following subproblem by using any UE minimization method. This yields a link flow vector 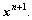

Step 3: Convergence test. If 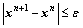 (ε is the convergence criterion), stop; If not, set n=n+1, and go to Step 2.
(ε is the convergence criterion), stop; If not, set n=n+1, and go to Step 2.
4 Numeral example
An URN is considered in Fig. 1 [20], which consists of 17 general nodes, 5 transfer nodes and 3 operation lines. Arbitrary two nodes can be seen as an OD pair.
The link parameters are listed in Table 1. Table 2 gives the networks parameters.
According to the augmented network method, the test URN is plotted as Fig. 2 [20]. It can be seen thatevery transfer node is divided into 4 virtual nodes and 6 virtual links. If two virtual nodes belong to the same operation line, the cost (time) is set zero. Otherwise, the cost (time) is equal to the transfer time. Therefore, the original figure can be extended to a graph with 37 nodes and 60 links.

Fig. 1 A test network [20]
Table 1 Link parameters

Table 2 Network parameters


Fig. 2 Augmented test network [20]
Let 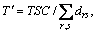 where
where 
 Figure 3 gives the change of the average cost T ′ of each person in the traffic system with capacity degradation θ for different demand degrees: lower, media and higher corresponding to 20, 40 and 60 respectively. It is found that the average cost T ′ decrease with the increase of coefficient θ, meaning the worsen performance for the larger bound capacity and higher demand. For example, the average cost T ′ is about 3300, 703 and 106 in higher, media and lower demand cases, respectively. Compared with 0.1, when the θ-value is set to 0.15, the average cost T′ has a drop of 70% approximately for drs=60.
Figure 3 gives the change of the average cost T ′ of each person in the traffic system with capacity degradation θ for different demand degrees: lower, media and higher corresponding to 20, 40 and 60 respectively. It is found that the average cost T ′ decrease with the increase of coefficient θ, meaning the worsen performance for the larger bound capacity and higher demand. For example, the average cost T ′ is about 3300, 703 and 106 in higher, media and lower demand cases, respectively. Compared with 0.1, when the θ-value is set to 0.15, the average cost T′ has a drop of 70% approximately for drs=60.

Fig. 3 Change of average cost with capacity degradation coefficient θ for different demand levels
The relationship among the total system cost TSC, the proportion p and capacity degradation coefficient θ for different demand levels is given in Fig. 4. Because the insensitive passengers have small δ2 and do not pay much attention to the effect of congestion, most of them will choose the shortest path (without much attention to the congestion effects) as their travel route. With the accumulation of passenger flow, the route with higher travel cost will not be chosen by sensitive passenger (much attention to the congestion effects). As a result, the flow distribution will be changed with the proportion p and coefficient θ which indicates that insensitive passengers have some effects on the path choice of sensitive ones, especially for the larger demand drs and p.

Fig. 4 Relationship among total system cost TSC, proportion p and capacity degradation coefficient θ for different demand levels
5 Conclusions
With the consideration of capacity degradation in augmented URN, a passenger flow equilibrium model is proposed to describe the travel choice behavior for two parts of passengers, insensitive and sensitive. The results are very important for us to understand the characteristics of degradable URN. Firstly, the demand has a key role in the degradable URN, which makes the average cost T ′ multiplier increase (or decrease). Furthermore, the obvious changes can be found in the degradable URN for capacity degradation coefficient θ. The smaller coefficient θ will make travel time in the URN more reliable.
Notations
RS OD set
TN Transfer node set
rs OD pair index, 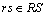
a Link index, 
λ Degree of risk aversion
i Passenger type, i=1 is sensitive passenger, and i=2 is for insensitive passenger
drs OD demand between pair rs
p Proportion of insensitive passengers
1-p Proportion of sensitive passengers
ta In-train cost of passenger on link a, 
Y(·) Extra cost caused by congestion in the train, which is a function of seat number of the train
 Time of passenger i in the train on link a,
Time of passenger i in the train on link a,  , i=1, 2
, i=1, 2
w Waiting time
th Transfer time between different lines
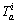 Link travel time of passenger i (including the time of in-train, waiting and transfer) with the consideration of risk aversion, i=1, 2
Link travel time of passenger i (including the time of in-train, waiting and transfer) with the consideration of risk aversion, i=1, 2
la Length of link a, 
L Distance between two platforms in the same transfer node
vt Running speed of train
vp Walking speed of people
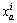 Flow of passenger i on link a,
Flow of passenger i on link a,  , i=1, 2
, i=1, 2
 Flow of passenger i on path k between OD pair
Flow of passenger i on path k between OD pair 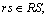 i=1, 2
i=1, 2
Xi Flow of transfer of node i, 
f Frequency of train
nseat Total seat number of train
ca Design capacity of link a
urs Minimum cost between OD pair rs
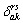 Path / link incidence variables
Path / link incidence variables
δi Sensitive parameter to congestion of sensitive and insensitive passengers respectively, i=1, 2, δ1>>δ2
References
[1] TIAN Qiong, HUANG Hai-jun, YANG Hai. Equilibrium properties of the morning peak-period commuting in a many-to-one mass transit system [J]. Transportation Research Part B, 2007, 41(6): 616-631.
[2] DAGANZO C F, SHEFFI Y. On stochastic models of traffic assignment [J]. Transportation Science, 1977, 11(3): 253-274.
[3] FISK C. Some developments in equilibrium traffic assignment [J]. Transportation Research Part B, 1980, 14(3): 243-255.
[4] LAMA W H K, GAO Z Y, CHAN K S, YANG H. A stochastic user equilibrium assignment model for congested transit networks [J]. Transportation Research Part B, 1999, 33(5): 351-368.
[5] NIELSEN O A. A stochastic transit assignment model considering differences in passengers utility functions [J]. Transportation Research Part B, 2000, 34(5): 377-402.
[6] CLARK S, WATLING D. Modelling network travel time reliability under stochastic demand [J]. Transportation Research Part B, 2005, 39(2): 119-140.
[7] SUMALEE A, TAN Z J, LAM W H K. Dynamic stochastic transit assignment with explicit seat allocation model [J]. Transportation Research Part B, 2009, 43(8/9): 895-912.
[8] SZETO W Y, LO H. Dynamic traffic assignment: Properties and extensions [J]. Transportmetrica, 2006, 2(1): 31-52.
[9] SIU B, LO H. Doubly uncertain transportation network: Degradable capacity and stochastic demand [J]. European Journal of Operational Research, 2008, 191(1): 166-181.
[10] SUN L J, JIN J G, LEE D H, AXHAUSEN K W, ERATH A. Demand-driven timetable design for metro services [J]. Transportation Research Part C, 2014, 46: 284-299.
[11] YIN Y, LAM W H K, IEDA H. New technology and the modeling of risk taking behavior in congested road networks [J]. Transportation Research Part C, 2004, 12(3): 171-192.
[12] BELL M G H, CASSIR C. Risk-averse user equilibrium traffic assignment: An application of game theory [J]. Transportation Research Part B, 2002, 36 (8): 671-682.
[13] CHAN K S, LAM W H K. Impact of road pricing on the network reliability [J]. Journal of the Eastern Asia Society for Transportation Studies, 2005, 6: 2060-2075.
[14] SUMALEE A, WATLING D P, NAKAYAMA S. Reliable network design problem: Case with uncertain demand and total travel time reliability [J]. Transportation Research Record: Journal of the Transportation Research Board, 2006, 1964(1): 81-90.
[15] NIKOLOVA E, STIER-MOSES N E. A mean-risk model for the traffic assignment problem with stochastic travel times [J]. Operations Research, 2014, 62(2): 366-382.
[16] CANTARELLA G E,  A, de LUCA S. Stochastic equilibrium assignment with variable demand: Theoretical and implementation issues [J]. European Journal of Operational Research, 2015, 241(2): 330-347.
A, de LUCA S. Stochastic equilibrium assignment with variable demand: Theoretical and implementation issues [J]. European Journal of Operational Research, 2015, 241(2): 330-347.
[17] JANG W. Travel time and transfer analysis using transit smart card data [J]. Transportation Research Record: Journal of the Transportation Research Board, 2010, 2144(2): 142-149.
[18] SUN Y S, XU R H. Rail transit travel time reliability and estimation of passenger route choice behavior [J]. Transportation Research Record: Journal of the Transportation Research Board, 2012, 2275(2): 58-67.
[19] ZHOU F, XU R H. Passenger flow assignment model for urban rail transit based on entry and exit time constraints [J]. Transportation Research Record: Journal of the Transportation Research Board, 2012, 2284(2): 57-61.
[20] ZHU W, HAO H, HUANG Z D. Calibrating rail transit assignment models with genetic algorithm and automated fare collection data [J]. Computer-aided Civil and Infrastructure Engineering, 2014, 29(7): 518-530.
[21] SUN L J, JIN J G, LEE D H, AXHAUSEN K W. An integrated Bayesian approach for passenger flow assignment in metro networks [J]. Transportation Research Part C, 2015, 52(1): 116-131.
[22] WU J J, SUN H J, GAO Z Y, HAN L H, SI B F. Risk-based stochastic equilibrium assignment model in augmented urban railway network [J]. Journal of Advanced Transportation, 2014, 48(4): 332-347.
[23] HARKER P T. Multiple equilibrium behaviors on networks [J]. Transportation Science, 1988, 22: 39-46.
[24] VAN V T, VAN V D, SMITH M J. Combined equilibrium in a network with partial route guidance [C]// Traffic Control Methods. New York: Engineering Foundation, 1990: 375-387.
[25] SHEFFI Y. Urban transportation networks: equilibrium analysis with mathematical programming methods [M]. Englewood Cliffs, New Jersey, USA: Prentice-Hall, 1985: 399.
(Edited by YANG Hua)
Foundation item: Project(71525002) supported by China National Funds for Distinguished Young Scientists; Projects(71271023, 71210001) supported by the National Natural Science Foundation of China; Project(RCS2015ZZ003) supported by the Research Foundation of State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, China
Received date: 2015-03-31; Accepted date: 2015-12-10
Corresponding author: WU Jian-jun, Professor; Tel: +86-13693097340; E-mail: jjwul@bjtu.edu.cn