J. Cent. South Univ. Technol. (2011) 18: 1589-1594
DOI: 10.1007/s11771-011-0876-2
Multi-domain modeling and simulation of proportional solenoid valve
LIU Yan-fang(刘艳芳)1, DAI Zhen-kun(戴振坤)1, XU Xiang-yang(徐向阳)1, TIAN Liang(田亮)2
1. School of Transportation Science and Engineering, Beihang University, Beijing 100191, China;
2. School of Engineering and Design, University of Sussex, Brighton BN1 9QT, UK
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: A multi-domain nonlinear dynamic model of a proportional solenoid valve was presented. The electro-magnetic, mechanical and fluid subsystems of the valve were investigated, including their interactions. Governing equations of the valve were derived in the form of nonlinear state equations. By comparing the simulated and measured data, the simulation model is validated with a deviation less than 15%, which can be used for the structural design and control algorithm optimization of proportional solenoid valves.
Key words: fluid mechanics; proportional solenoid valve; dynamic characteristic; multi-domain modeling; simulation
1 Introduction
Proportional solenoid valve is a key control and executing element in industries such as vehicle, construction, aircraft, and mining, whose characteristic is governed by a couple of interacting electro-magnetic, mechanical and flow equations. It has been successfully used for many years due to its high accuracy and robustness which are critical factors for system regular operation. Owing to its importance, a considerable amount of researches on the performance of proportional solenoid valve have been conducted with various methods.
Some dynamic performance simulation research works have been presented to predict the dynamic response of proportional solenoid valve [1-2]. The finite element method (FEM) was usually adopted to analyze the magnetic field and electromagnetic force [3-6]. Hardware-in-loop (HIL) tests of solenoid valve were implemented to view its reliability and performance [7-9]. Efforts on the solenoid driving circuits were made to improve the response performance [10-12]. SETHSON et al [13] proposed a simple model for a 2/2 hydraulic solenoid valve in which the model parameters are tuned to yield good agreement between the measured and the simulated variables. TAGHIZADEH et al [14] developed a nonlinear dynamical model of a pneumatic fast switching valve of which the electro-magnetic, mechanical and fluid subsystems were investigated including their interactions. MAITI et al [15] analyzed the dynamic performance of a proportional pressure relief valve, in which the simulation results were obtained using the MATLAB- SIMULINK environment. DASGUPTA and WATTON [16] proposed a nonlinear dynamic model of a proportional solenoid controlled piloted relief valve through Bondgraph simulation technique, in which higher order dynamics was predicted. WANG et al [17] studied the modeling of the fluid and mechanical subsystems of hydraulic valves using the software SimulationX. However, very few authors have treated the modeling of proportional solenoid valve on a system level to analyze its dynamic characteristics.
As a system, a proportional solenoid valve involves several physical domains and its basic task is to transfer energy among electrical, magnetic, mechanical and hydraulic domains. Various non-linear effects such as flow forces, valve dynamics, orifice flow and chamber fluid compressibility should be taken into account in order to analyze its dynamic characteristics accurately. Therefore, modeling the proportional solenoid valve accurately is a challenging work. In this work, the modeling and identification of a proportional solenoid valve are presented.
2 Structure of valve
Figure 1 shows a simplified schematic view of a proportional solenoid valve (open state) on an 8-speed automatic transmission under study. The solenoid valve is mainly composed of a coil, a core spool and a return spring. Through the moving of the core spool, the valve opens and closes. When the solenoid is energized by DC voltage, the resultant magnetic force displaces the moving spool against the return spring, the valve opens and a flow cross section develops through an orifice.
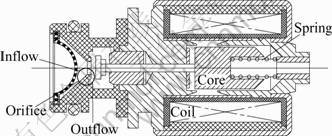
Fig.1 Schematic diagram of proportional solenoid valve (open state)
As shown in Fig.1, a proportional solenoid valve can be decomposed into three subsystems: the electro-magnetic subsystem, mechanical subsystem and fluid subsystem. The electro-magnetic subsystem consists of an electrical and magnetic circuit included in a solenoid. The mechanical subsystem consists of a mass, spring and damper under the effect of magnetic force and hydraulic pressure. These two subsystems behave dynamically and have transient response. The fluid subsystem is the valve orifice, through which the fluid flow is controlled by moving the spool position.
3 Valve modeling
A proportional solenoid valve is a complex technical system whose static and dynamic characteristics are governed by a couple of interacting electro-magnetic, mechanical and flow equations. Different subsystems of a proportional solenoid valve are investigated and the governing equations are derived in the form of nonlinear state equations. Therefore, the solenoid current, the spool position and the spool velocity are selected as state variables.
In developing the valve model, the following assumptions are made:
1) A constant source of supply to the inlet port of the valve is considered;
2) The fluid considered for the analysis has Newtonian characteristics;
3) The spring is assumed to be linear;
4) With the opening of the valve ports, the dynamic flow force acting on the valve spool is neglected and only the steady state flow force is considered;
5) The positional striction of the valve spool has not been accounted.
3.1 Electro-magnetic subsystem
This subsystem is used to transfer the input voltage to an electro-magnetic force on the spool of the valve. The magnetic circuit of the valve can be represented by a circuit of discrete resistances [12]. Therefore, the electro- magnetic portion in Fig.1 can be translated into a magnetic circuit which consists of iron resistances (R1, R2 and R4), radial air gaps (R3 and R5), a circular variable air gap with stray field (F1), an invariable stray field (G1), a constant air gap with stray field (G2) and an electromagnetic transformer (W1), as shown in Fig.2.
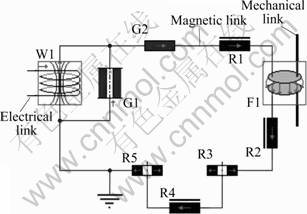
Fig.2 Equivalent magnetic circuit of proportional solenoid valve
According to Kirchihoff’s Voltage Law, the following equation must be held for each loop in the magnetic circuit:
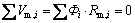 (1)
(1)
where Vm is the magnetic voltage; Rm is the magnetic resistance; i is the number of the components of the magnetic circuit.
With the definition of the magnetic flux Φ, the following statement is applied to any connection between these components of the magnetic circuit:
 (2)
(2)
The coupling between electric and magnetic quantities through W1 can be deduced from Maxwell’s equation:
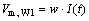 (3)
(3)
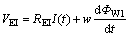 (4)
(4)
where w is the number of windings; I(t) is the solenoid current; VEI is the electric voltage; REI is the electric resistance; t is the time..
The constitutive relation of an iron magnetic resistance is determined by its geometry and iron material properties. The characteristics of the iron material can be described by the relationship between the magnetic field strength H and the magnetic flux density B in the form of a bistable sigmoid [12], which is strongly nonlinear. Here, the hysteretic effect is disregarded. Because of the regular geometries of the iron magnetic resistance (R1, R2 and R4), the magnetic voltage and the magnetic flux of an iron resistance can be approximated as
 (5)
(5)
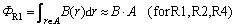 (6)
(6)
where H is the magnetic field strength; B is the magnetic flux density; W is the path along the main field in the iron magnetic resistance from the positive to the negative magnetic pin; A is the magnetic cross-section area with normal in B direction; l is the magnetic length in direction of H.
Thus, the iron resistance (R1, R2 and R4) is derived from
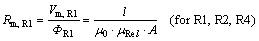 (7)
(7)
The circular air gap F1 is the interface between magnetic subsystem and mechanical subsystem. The stray field is taken into account in addition to the magnetic flux in the air gap. The magnetic resistance of the air gap depends strongly non-linearly on the geometry. The magnetic flux Φ is calculated from its magnetic resistance including its stray flux:
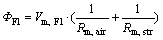 (8)
(8)
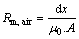 (9)
(9)
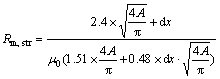 (10)
(10)
where Rm,air is the air gap resistance; Rm,str is the magnetic resistance of its circular stray field; dx is the air gap length; A is the cross-section area.
So, the magnetic resistance of the circular air gap F1 including the stray flux is resulted from
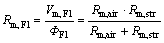 (11)
(11)
Therefore, the magnetic force Fm,F1 is resulted from
 (12)
(12)
As for the constant air gap G2, the magnetic resistance can also be deduced according to Eqs.(8)-(11). The only difference is that the air gap G2 has a constant length while F1 has a variable length.
The winding space can be modeled by an invariable stray field component G1. The magnetic resistance is derived from
 (13)
(13)
where dout is the outer diameter of the winding space, din is its internal diameter, and l is the winding length.
In the radial air gaps, R3 and R5, the space bearing a magnetic flux forms a hollow cylinder. Then, the magnetic resistance is resulted from
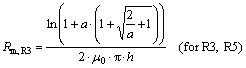 (14)
(14)
where h is the height of the space of the stray field; the variable a depends on its geometry:
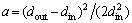
3.2 Fluid subsystem
As for the orifice whose turbulent losses are dominant, its hydraulic resistance is described by its geometry. The volume flow Qorifice at the orifices, as shown in Fig.3, is calculated from
 (15)
(15)
where Aflow is the cross-sectional area; αD is the flow-rate coefficient; Δp is the pressure difference between point 1 and point 3, Δp=p1-p3; ρ is the upstream density of the fluid.
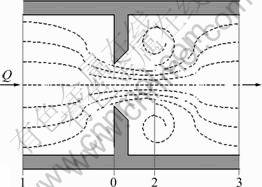
Fig.3 Schematic diagram of orifice
According to Hagen-Poiseuille’s law, a laminar pressure loss, Δplam, is added to the turbulent losses:
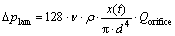 (16)
(16)
where 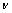 is the upstream kinematic viscosity, ρ is the upstream density, and d is the orifice diameter.
is the upstream kinematic viscosity, ρ is the upstream density, and d is the orifice diameter.
The hydrostatic force Fhy on the core spool is obtained from
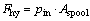 (17)
(17)
where pin is the pressure of the valve inlet and Aspool is the cross-sectional area of the core spool.
According to the fundamental momentum equation, the steady-state flow force in the axial direction is equal to the momentum difference between the fluid flow into and out of the control volume. Since the flow velocity at the outlet can be neglected compared with the one at the inlet, the axial flow force on the spool can be simplified to
 (18)
(18)
where vin is the flow velocity at the inlet and θ is the flow angle depending on the opening state of the spool.
3.3 Mechanical subsystem
The transient response of the mechanical subsystem can be represented by Newton’s second law as
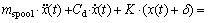
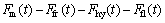 (19)
(19)
where mspool is the mass of the core spool; Cd is the damping coefficient; K is the spring stiffness coefficient; x is the displacement of the core spool; δ is the spring pre-tension; 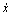 is the velocity of the core spool;
is the velocity of the core spool; 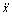 is the acceleration of the core spool; Fm is the magnetic force (see Eq.(12)); Fhy is the hydrostatic force (see Eq.(17)); Ffr is the slipping frictional force; Ffl is the axial steady-state flow force on the spool due to the momentum change of the fluid flow (see Eq.(18)).
is the acceleration of the core spool; Fm is the magnetic force (see Eq.(12)); Fhy is the hydrostatic force (see Eq.(17)); Ffr is the slipping frictional force; Ffl is the axial steady-state flow force on the spool due to the momentum change of the fluid flow (see Eq.(18)).
4 Model validation
In order to analyze the dynamic characteristics of the proportional solenoid valve and to verify the validation of the above simulation model, a hydraulic test bench was set up, as shown in Fig.4(a). The inlet orifice was set to be 0.9 mm. The pressure and the volume flow at the orifice inlet were measured by two sensors labeled with P and Q, respectively, as shown in Fig.4(b).
The supply pressure was set to be 550 kPa. By controlling PWM width, the input current was increased from 0 to 1 000 mA monotonously and then went back to 0 mA. Commonly, a dither current is adopted to keep the core spool dithering to speed up its dynamic response. Thus, a 50 Hz dither current was added to the control signal. Amplitudes of the dither current were set according to empirical data. Figure 5 shows the dither signal which was added to the PWM control signal for testing. Automatic transmission fluid ATFSSVIII from Sinopec Group was used in the experiment at the standard evaluating temperature of 40 °C.
5 Simulation results and discussion
Combined with the above electro-magnetic, fluid and mechanical subsystem models, the complete simulation model of a proportional solenoid valve was built based on the multi-domain simulation software platform SimulationX, whose dynamic characteristics were simulated.

Fig.4 Test bench for proportional solenoid valves: (a) Test bench picture; (b) Schematic diagram
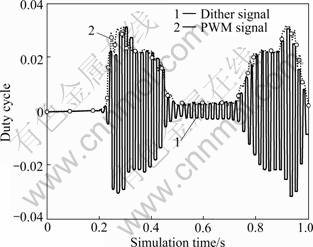
Fig.5 Dither control signal added to PWM control signal
Figure 6 displays the calculated dynamic characteristic of the hydraulic portion of the proportional solenoid valve, which shows the strong nonlinearity of the pressure and the volume flow with respect to the motion of the spool.
Figure 7 shows the calculated hydraulic force, spring force, flow force and magnetic force with respect to the current, respectively. It is obvious that the hydraulic force and the magnetic force influence the motion of the core spool significantly.
Figures 8 and 9 show the hydraulic pressure and the volume flow controlled by the proportional solenoid valve with respect to the control current, respectively. It is obvious that the simulation result approximates the test data very well. Both results show that the pressure and the volume flow have strong nonlinear performance with an obvious hysteretic feature on the ascent stage and descent stage. So, the modeling method of the proportional solenoid valve is capable.
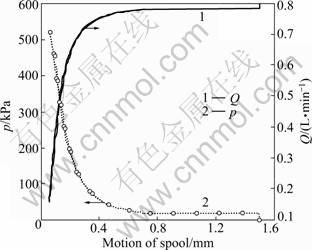
Fig.6 Simulated pressure and volume flow
Fig.7 Simulated forces on core spool
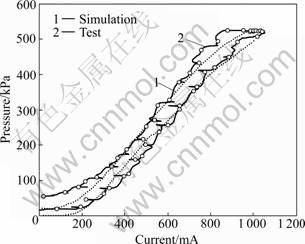
Fig.8 Measured and simulated pressure
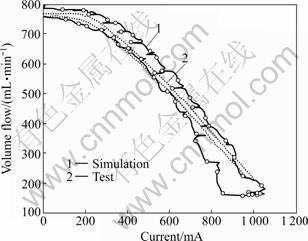
Fig.9 Measured and simulated volume flow
The simulation result has less than 15% deviation with the test result. The main reason is that some of the model parameters are hard or impossible to measure, especially when it comes to magnetic material properties. Even for those parameters which can be directly obtained by measurement, there may be measurement errors.
Based on this model, optimized control algorithm for the PWM width could be developed to obtain the required hydraulic pressure.
6 Conclusions
1) A multi-domain nonlinear dynamic model of a proportional solenoid valve system is developed in form of nonlinear state equations and validated by experiment measurements.
2) This model successfully predicts the dynamic characteristics of the valve and can be used as a powerful computational and simulation tool for valve design and algorithm optimization.
3) Unknown parameter and parameter measurement errors are the main reasons for the simulation deviation.
References
[1] RAHMAN M F, CHEUNG N C, LIM K W. Modeling of a non-linear solenoid towards the development of a proportional actuator [C]// Proceedings of the 5th International Conference on Modeling and Simulation of Electrical Machines, Converters and Systems. Saint Nazaire, France, 1996: 121-128.
[2] DEEPIKA D, SCOTT S, BIRGIT K. Multi-domain modeling and simulation of a linear actuation system [M]. Pittsburgh: Ansoft Corporation, 2003: 58-70.
[3] XIE Hai-bo, L? Zhen-jun, YANG Hua-yong, ZHEN Yu, ZHANG Jin. Static and dynamic performance research on proportional solenoid [C]// Proceedings of the 2010 IEEE International Conference on Mechanic Automation and Control Engineering. Wuhan, China: IEEE, 2010: 5952-5955.
[4] HANG Tian, SHENG Ding, GAO Zhi-qiang, JI Da-xi, LIU Yi-qun, HUANG Peng-chao, XU Hui, LI Xiao-feng, BAO Zheng-qiang. The analysis research of design the magnetic field of the solenoid [C]// Proceedings of the 2010 IEEE International Conference on Vacuum Electronics. Monterey, CA: IEEE, 2010: 487-488.
[5] ALBERT S. Transient simulation to improve the solenoid dynamics in pneumatic valves [D]. Aachen: Institute for Fluid Power Drives and Controls of RWTH, 2004.
[6] LIU Qiang-feng, BO Han-liang, QIN Ben-ke. Design and analysis of direct action solenoid valve based on computational intelligence [J]. Nuclear Engineering and Design, 2010, 240: 2890-2896.
[7] CHEUNG N C, RAHMAN M F, LIM K W. Simulation and experimental studies towards the development of a proportional solenoid [C]// The 28th Universities Power Engineering Conference. Staffordshire, UK: Staffordshire University, 1993: 582-587.
[8] JIANG Yang, LIU Hong-yi, LUO Zhong, CHEN Xi. Research on intelligent test system for solenoid valve [J]. International Journal of Intelligent Engineering & Systems, 2009, 2(2): 25-31.
[9] CHU Liang, HOU Yan-li, LIU Ming-hui, LI Jun, GAO Yi-min, EHSANI M. Study on the dynamic characteristics of pneumatic ABS solenoid valve for commercial vehicle [C]// Proceedings of the 2007 IEEE International Conference on Vehicle Power and Propulsion. Arlington, TX: IEEE, 2007: 641-644.
[10] LU F K, JENSEN D S. Potential viability of a fast-acting micro-solenoid valve for pulsed detonation fuel injection [C]// The 41st AIAA Aerospace Sciences Meeting. Reno, Nevada: AIAA, 2003: 0881-0888.
[11] LIU Hui, GU Hong-bin, CHEN Da-wei. Application of high-speed solenoid valve to the semi-active control of landing gear [J]. Chinese Journal of Aeronautics, 2008, 21: 232-240.
[12] WILLIAMS M C, VOGELSONG R S, KENNETH K S. Simulation and modeling of nonlinear magnetics [C]// Proceedings of the 1994 IEEE International Symposium on Circuits and Systems. Seattle, America: IEEE, 1994: 8(1b): 1-12.
[13] POHL J, SETHSON M, KRUS P, PALMBERG J O. Modeling and validation of a fast switching valve intended for combustion engine valve trains [J]. Proceedings of the Institution of Mechanical Engineers Part I: Journal of System and Control Engineering, 2002, 216: 105-116.
[14] TAGHIZADEH M, GHAFFARI A, NAJAFI F. Modeling and identification of a solenoid valve for PWM control applications [J]. Computes Rendus Mecanique, 2009, 337: 131-140.
[15] MAITI R, SAHA R, WATTON J. The static and dynamic characteristics of a pressure relief valve with a proportional solenoid-controlled pilot stage [J]. Proceedings of the Institution of Mechanical Engineers Part I: Journal of System and Control Engineering, 2002, 216: 143-156.
[16] DASGUPTA K, WATTON J. Dynamic analysis of proportional solenoid controlled piloted relief valve by Bondgraph [J]. Simulation Modeling Practice and Theory, 2005, 13: 21-38.
[17] WANG Shu-han, XU Xiang-yang, LIU Yan-fang, TENBERGE P. Design and dynamic simulation of hydraulic system for a new automatic transmission [J]. Journal of Central South University of Technology, 2009, 16(4): 697-701.
(Edited by YANG Bing)
Foundation item: Project(2008ZHZX1A0502) supported by the Independence Innovation Achievements Transformation Crucial Special Program of Shandong Province, China
Received date: 2010-08-06; Accepted date: 2011-04-09
Corresponding author: DAI Zhen-kun, PhD Candidate; Tel: +86-10-82338121; E-mail: zhenkun@buaa.edu.cn