基于多重网格法的MT正演模型边界截取
柳建新1,郭荣文1, 2,童孝忠1,邓小康1,郭振威1
(1. 中南大学 地球科学与信息物理工程学院,湖南 长沙,410083;
2. School of Earth and Ocean Sciences, University of Victoria, Victoria B.C., V8W 3P6, Canada)
摘要:为了验证基于多重网格法边界截取的效果,通过数值模拟,分别对大地电磁法问题的均匀半空间模型和三层模型进行基于多重网格法的边界截取研究和分析。采用加权平均法产生粗网格上系数矩阵,并与传统的方法对比。研究结果表明:粗网格加权平均法的渐进收敛性明显比Galerkin法(采用简单的插值矩阵)的好,但比粗网格近似的几何法的渐进收敛性略差;收敛性的广义Fourier谱分析在大地电磁法中对介质的非连续性不敏感,不能区分模型参数变化所引起的收敛性变化;随着边界截取的增加,满足特定收敛标准的数值解与理论解偏差增大;当截取到的深度约为趋附深度的2倍时,截取后的计算结果接近理论值,说明基于多重网格法的边界截取有效。
关键词:多重网格法;边界截取;粗网格;收敛性;大地电磁法
中图分类号:P631.3 文献标志码:A 文章编号:1672-7207(2011)11-3429-09
Boundary truncation of magnetotelluric modeling based on multigrid method
LIU Jian-xin1, GUO Rong-wen1, 2, TONG Xiao-zhong1, DENG Xiao-kang1, GUO Zhen-wei1
(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;
2. School of Earth and Ocean Sciences, University of Victoria, Victoria B.C., V8W 3P6, Canada)
Abstract: Boundary truncation was applied for homogeneous half-space model and three-layer model based on the multigrid method. Compared to traditional coarse grid approximations, an average weighted method was used to generate the coarse grid approximation and general Fourier analysis was carried out for convergence analysis. Utilizing cycles or component of multi-grid method, the modeling area was reduced to improve modeling efficiency. The numerical results for boundary truncation were compared with numerical results by direct solver. The results show that the weighted average method has a better convergence behavior than Galerkin method and slightly poorer convergence than geometric method. General Fourier analysis is not sensitive to conductivity discontinuities and can not demonstrate the convergence differences caused by the discontinuities. As the truncation increases, deviation from the theoretical results becomes more obvious. When the boundary is truncated to around twice the skin depth, and the results are well approximated with theoretical results. In the log space (or just log frequency), when the truncated boundary value cannot well represent the real value, the calculated absolute electrical field (or phase) tends to move up and down at the same level with respect to frequency.
Key words: multigrid method; boundary truncation; coarse grid; convergence; magnetotelluric method
大地电磁法正演中边界条件的处理对正演的效率和精度有重要的影响,它在正演研究中具有重要的作用[1-6]。1976年Weaver等[1]提出将渐近边界条件应用到二维的大地电磁法正演中,Zhdanov等[2]将渐进边界条件扩展到三维大地电磁法的正演中,以减少计算区域。类似的吸收边界条件在其他非大地电磁法的电磁法中也得到广泛应用[7-9],使得本应是无限区域的模拟通过合理强加某种吸收边界便可以用有限计算区域进行近似。另一种是通过积分方程法或特征向量展开等全局方法与微分方程法进行某种综合[10-12],如积分法和有限单元法、特征向量展开和有限单元法等等。在异常区域边界内采用有限元等微分方程法,边界外采用积分方程等全局法,通过边界连续性进行耦合。也有的采用粗网格的有限差分法获取近似边界条件,然后在更小区域采用更细网格的有限差分法求解。多重网格法可分为几何多重网格法[13]和代数多重网格法[14],其思想是将平滑后的误差比较准确地投影到粗网格上,在粗网格上以更小的代价求解方程。由于它每次循环的计算量与未知数量N呈线性关系,因此,它在涉及稀疏大型矩阵计算的工程领域中应用相当广泛[14-15]。多重网格法在电磁法领域应用广泛[18-20],或作为直接解法或作为预处理。利用多重网格法的特点,将其中某个循环的求解作为压缩边界条件,以缩小计算区域。在多重网格法中,粗网格系数矩阵的获取对该方法求解的收敛性有重要的影响。目前,主要用到的粗网格近似有基于几何形状的几何剖分法[13]和基于矩阵操作符的代数剖分法[14]。几何剖分法具有物理意义强的特点,但用于复杂模型(比如几何形状复杂和参数变化大)时困难较大。代数剖分对复杂模型比较适应,并不考虑问题本身的特点,结合这两者的特点产生粗网格系数矩阵。利用多重网格法对求解区域进行边界截取,采用加权平均法对粗网格系数矩阵进行近似。通过均匀半空间模型和3层模型2个事例,采用广义的Fourier谱分析对粗网格近似的加权平均法和传统的Galerkin法收敛性进行对比,然后,对以上2个模型基于多重网格法对边界进行截取,并对其效果进行分析。
1 一维亥姆霍兹方程的边值问题
为了便于验证基于多重网格法边界截取的有效性,应尽量使考查的问题简单。一维大地电磁法问题是一个很好的选择,容易扩展到高维问题(比如二维和三维问题)。下面讨论大地电磁法的一维边值问题,在直角坐标系下和SI国际单位制下,沿x方向电场分量Ex的准静态亥姆霍兹方程可以从麦克斯韦方程组得到:
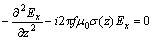 (1)
(1)
其中: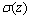 为在深度z的电导率;f为频率;μ0为真空中的磁导率。
为在深度z的电导率;f为频率;μ0为真空中的磁导率。
求解式(1)需要知道它的边界条件[16-17]。在大气中,由于磁场在y方向的分量在数学上可以近似为常数,通常取单位常数。在大气的上边界上,从麦克斯韦方程组可以得到如下上边界条件:
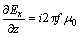 (2)
(2)
在底边界上z→∞时,该处场衰减为0。以上就是一维亥姆霍兹方程的边值问题,可以通过解析求解或数值求解得到。
如果利用有限差分法近似以上边值问题,将大地分成电导率为σ1, σ2, …, σN的N层,每层的界面在z1, z2, …, zN处。在zi接触面上取电场强度Ei,就可以将以上边值问题以均匀等距?h离散成有限差分的形式。式(1)在i点处可表示为:
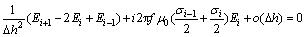 (3)
(3)
边界条件为:
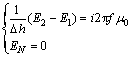 (4)
(4)
将所有点组合成矩阵形式,以上边值问题表示成:
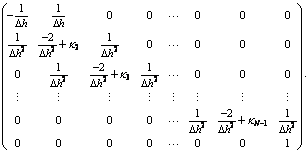
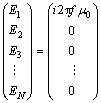 (5)
(5)
其中: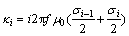 。式(5)简写成:
。式(5)简写成:
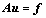 (6)
(6)
其中:A为复系数矩阵;u为离散后场值向量;f为式(5)的右端向量,也叫“源项”。对式(6)可以用线性方程组的直接解法如Gauss消去法、迭代法如静态的Gauss-Seidel法和动态的基于Klylov子空间的共扼梯度法[18]等求解。本文主要研究采用多重网格法求解。
2 多重网格法
假设在以均匀步长h剖分的细网格上,
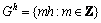 (7)
(7)
式(6)可表示为:
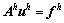 (8)
(8)
其中:Ah,uh和f h分别为该网格上的系数矩阵、场向量和源项。在粗网格上,
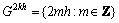 (9)
(9)
通常该粗网格的系数矩阵A2h可以通过几何法或代数法求得。几何法是用更大步长如2h来剖分模拟区域以近似微分方程(比如亥姆霍兹方程),方式有节点法和单元中心法。代数法基于矩阵操作符(也就是Restriction和Prolongation操作符及细网格操作符),并不关心问题的实际物理特征如参数的不连续性等。代数方法可以通过Galerkin法求得:
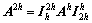 (10)
(10)
其中: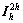 表示Restriction操作符;
表示Restriction操作符;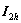 表示Prolongation操作符。只要求得细网格上的近似系数矩阵Ah,
表示Prolongation操作符。只要求得细网格上的近似系数矩阵Ah,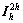 和
和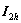 ,不管是不是连续及形状的复杂程度,都可以得出粗网格的近似。
,不管是不是连续及形状的复杂程度,都可以得出粗网格的近似。
本文提出了一种基于细网格系数矩阵的粗网格系数矩阵构建方法。这种方法是针对参数变化比较大时,通过加权平均得到粗网格点上的参数。利用细网格系数矩阵包含足够的模型信息这一特点,根据自己预定的剖分,将系数矩阵的每一行看成是1个节点,对邻近几个节点变化的模型参数进行加权平均得到相应节点的参数,然后考虑剖分步长得到粗网格系数矩阵。以标准剖分为例(即粗网格的步长是细网格的2倍),不管某一节点与前后节点的物性是否连续,用相邻连续几个节点的加权平均得到新节点的变化参数。为了便于表示,没有考虑步长的变化,在粗网格上变化的参数用三点加权平均公式表示为
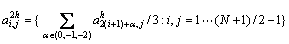 (11)
(11)
其中: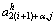 表示更细网格的相邻点
表示更细网格的相邻点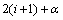 (
(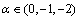 )的可变参数。当某一节点两边物性变化时,方程本身并不能区分和表示这种变化,而是把它当成一种平均变化的过程[16]。这样产生的系数矩阵既具有代数多重网格法的简单特点,又考虑到了问题的模型变化,对于参数变化大的问题可以改善传统几何多重网格法的收敛性。
)的可变参数。当某一节点两边物性变化时,方程本身并不能区分和表示这种变化,而是把它当成一种平均变化的过程[16]。这样产生的系数矩阵既具有代数多重网格法的简单特点,又考虑到了问题的模型变化,对于参数变化大的问题可以改善传统几何多重网格法的收敛性。
多重网格法主要有以下3步(以V型为例,W型的过程与V型的相似)。
(1) 对高频误差的预前松弛平滑。在细网格Gh上,高频误差通过某些平滑算法如Jacobi法,Gauss-Seidel法及其相应的变形(比如外插值的超松弛法和欠松弛法)等对式(8)以某一初值进行v1次平滑得到vh。矩阵 A可以分解为D-L-U(其中D为对角矩阵,L为下三角矩阵,U为上三角矩阵)。Jacobi外插值欠松弛法的误差传递矩阵为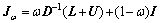 ,Gauss-Seidel外插值超松弛法的误差传递矩阵为
,Gauss-Seidel外插值超松弛法的误差传递矩阵为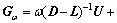
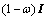 。其中:
。其中: 为加权因子,I为单位矩阵。
为加权因子,I为单位矩阵。
(2) 粗网格上的误差近似。通过步骤(1)的平滑处理,低频误差可以有效地在粗网格G2h上进行近似,使求解的工作量大大减少。在几何多重网格法中,可以在细网格的基础上进行“注入“或“加权”粗化。“注入”粗化保留原有细网格上奇数点(也可以保留偶数点),把偶数点(奇数点)去除而产生粗网格的一种方法;“加权”粗化是通过相邻若干点的加权产生相应粗网格点的一种方法。这时细网格的低频误差以余差的形式投影到粗网格上,即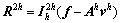 ,产生的误差方程组为
,产生的误差方程组为 (其中
(其中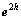 为该网格上的误差向量)。对误差方程组重复步骤(1)和(2),直到k达到定义的最大值(最粗网格)为止,在最粗网格上对方程组
为该网格上的误差向量)。对误差方程组重复步骤(1)和(2),直到k达到定义的最大值(最粗网格)为止,在最粗网格上对方程组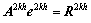 进行求解。其中:
进行求解。其中: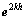 为最粗网格的误差;
为最粗网格的误差;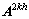 和
和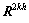 分别为最粗网格的系数矩阵和余差向量。
分别为最粗网格的系数矩阵和余差向量。
(3) 误差矫正及预后平滑处理。第(2)步完成后,将误差结果通过Prolongation操作符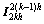 投影回更细网格,对误差进行矫正:
投影回更细网格,对误差进行矫正: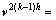
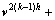
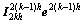 。重复这一过程直到最细网格
。重复这一过程直到最细网格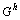 。以矫正后的
。以矫正后的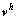 为初值对式(8)进行
为初值对式(8)进行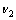 次平滑,循环以上过程直到满足预设的收敛标准为止。
次平滑,循环以上过程直到满足预设的收敛标准为止。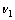 和
和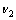 的选择影响到多重网格法的收敛性,
的选择影响到多重网格法的收敛性,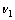 和
和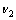 越大,收敛越快,通常情况下取少数几次即可。
越大,收敛越快,通常情况下取少数几次即可。
对于边界截取,利用多重网格法的少数几次循环近似解插值以得到任意边界条件。首先利用多重网格法对式(5)的传统边值问题进行若干次循环,然后,将所得结果进行插值以得到任意的边界条件。在离异常体较远处(除空气),电场强度变化比较平滑,经过几次多重网格法的循环,这些地方的计算值可以近似表示该处的实际传播值,达到压缩边界条件的目的。
3 收敛性分析
3.1 广义Fourier谱分析
由于式(8)的系数矩阵为复数,因此,以下分析如没有特别说明,都是基于复数域。广义Fourier谱分析的定义是通过选择误差传递矩阵的特征向量作为基函数,特征值作为衰减量,预测和分析多重网格法的收敛性。要获得这些量,通常需要进行大量的计算,甚至相当于求解方程组本身(这是在实际中用得少的原因)。它包含十分丰富的收敛性信息,分析传递矩阵的特征值[19-20]和特征向量,能直观准确地分析和预测某种求解方法收敛性。在多重网格算法中,粗网格上产生的系数矩阵较小,容易实现在粗网格上的广义Fourier谱分析。
在一般的平滑方法(如超松弛法)中,将式(8)中的系数矩阵Ah分解为:
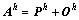 (12)
(12)
假如以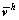 为初值,经过1次平滑后得到
为初值,经过1次平滑后得到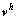 ,循环表达式表示为:
,循环表达式表示为:
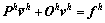 (13)
(13)
平滑前、后的误差分别表示为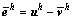 和
和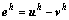 ,得到:
,得到:
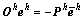 (14)
(14)
假设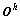 是可逆的,式(14)写成:
是可逆的,式(14)写成:
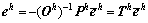 (15)
(15)
其中: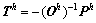 。将
。将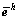 投影到Th的特征向量空间为:
投影到Th的特征向量空间为:
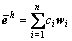 (16)
(16)
其中:wi为第i个Th的特征向量;ci为对应系数;n为所构成向量空间的维数(非线性相关的特征向量数)。因此,式(15)可变成:
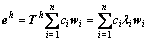 (17)
(17)
其中: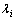 为Th的第i个特征值,也称为放大系数。
为Th的第i个特征值,也称为放大系数。
在多重网格法中,要求能有效地衰减高频误差成分,低频误差采用粗网格矫正。定义前半段特征值对应的特征向量为低频分量,后半段为高频分量。得到平滑率为
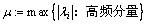 (18)
(18)
对于二重及二重以上的收敛性分析,把最低重定义在最粗网格上,假设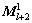 表示第l?(1, …, k-2)重分析的误差传递矩阵,则有[27]:
表示第l?(1, …, k-2)重分析的误差传递矩阵,则有[27]:
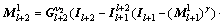
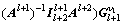 (19)
(19)
通过循环直到 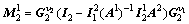 为止。其中:
为止。其中: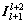 和
和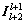 分别是l+2重到l+1重的转换矩阵和相反的转换矩阵;
分别是l+2重到l+1重的转换矩阵和相反的转换矩阵;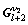 和
和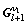 分别为l+2重和l+1重上平滑矩阵;
分别为l+2重和l+1重上平滑矩阵;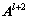 和
和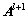 分别为l+2重和l+1重上的系数矩阵;
分别为l+2重和l+1重上的系数矩阵;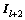 和
和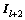 对应于l+2重和l+1重的单位矩阵;γ表示
对应于l+2重和l+1重的单位矩阵;γ表示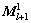 的循环次数。同理可得收敛因子为:
的循环次数。同理可得收敛因子为:
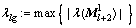 (20)
(20)
其中: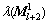 表示矩阵
表示矩阵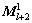 的特征值。
的特征值。
3.2 特征值及特征向量谱的空间转换
特征值和特征向量谱对研究线性方程组求解方法的收敛性非常有用,它们提供了几乎所有的收敛信息。但大部分只局限于对特征值谱进行研究[21],很少对特征向量进行分析。在复数域中,特征值一般是在复数平面上表示,定性判断一个系数矩阵的收敛性主要通过判断这些特征值的集中程度,很难从谱分析图上直观定量得到它的收敛性。这里将特征值和特征向量谱从复数域转换到实数域,再进行收敛性分析。
假设特征值或特征向量的某个分量元素为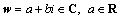 ,
,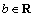 ,首先定义复数域到实数域的一个映射:
,首先定义复数域到实数域的一个映射:
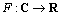 (21)
(21)
可通过以下转换将特征值或特征向量的某个分量转换到实数域中:
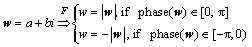 (22)
(22)
这样,可以直观地呈现特征值或特征向量谱的含义,很好地判断某种方法的收敛性。
4 结果分析
4.1 加权平均法与传统法粗网格系数矩阵产生法的收敛性广义Fourier谱分析
考察电磁波的频率f=3 Hz时一维的大地构造。首先以电导率为0.01 S/m的均匀半空间模型为例,接着分析以一电导率为0.1 S/m、厚度为600 m的良导体嵌入电导率为0.01 S/m的均匀半空间1.2 km处的三层模型,采用不同粗网格系数矩阵近似对收敛性进行 对比。
Galerkin法采用简单的点插值得到插值矩阵。对于一维均匀半空间模型,利用三重V型网格算法对有限差分离散化的亥姆霍兹方程进行求解,利用超松弛法作为高频误差的平滑方法,预前、预后平滑次数分别为1,加权因子ω为1.0,收敛性可对比当前计算误差与预设误差来判断。图1所示为不同粗网格近似的广义Fourier谱分析的特征值谱。从图1可见:3种方法在高频段特征值谱形态很相似,对高频分量收敛效果相近;在最低频段,基于Galerkin法(图1(a))的粗网格系数矩阵近似的最低频误差分量衰减率接近于1,收敛非常慢。几何法与加权平均法收敛的特征值谱形态相似,在最低频段,误差的收敛性明显比Galerkin法的好。表1所示为3种粗系数矩阵近似法重数不同的广义Fourier谱分析结果,其中r3g表示三重网格收敛性的数值解。从表1可见:三重广义Fourier谱分析与收敛性渐近估计的数值解比较接近。
对于3层模型,采用与均匀半空间模型相同的多重网格法分量参数和求解步骤。图2所示为该模型不同粗网格近似的广义Fourier谱分析的特征值谱图。从图2可以得出3种方法对高频段误差有相似的收敛行为。与前例相似,Galerkin法对低频误差衰减明显比几何法和加权平均法的要慢。与均匀半空间模型对比发现:对于几何法和加权平均法,参数的不连续性给收敛性带来一定的影响(使收敛性稍微变差)。表2显示3种粗网格近似法重数不同的广义Fourier谱分析结果。可以得出三重广义Fourier谱分析结果与收敛渐进估计的数值计算结果相一致,Galerkin法对低频误差的衰减明显比几何法和加权平均法的要慢,几何法和加权平均法的收敛性相接近(几何法收敛性稍好),低重分析结果与数值解偏差大。对比表1和表2发现:广义Fourier谱分析在大地电磁法中对介质的非连续性不敏感,对边界变化较敏感。
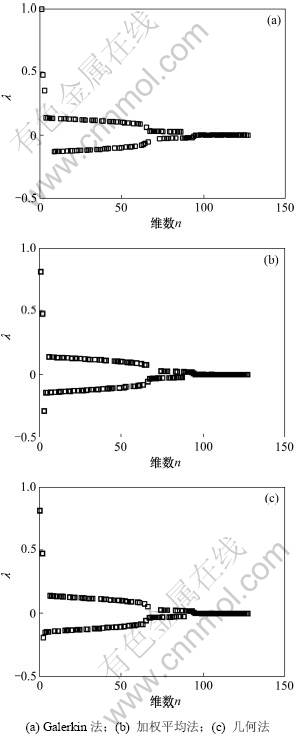
图1 均匀半空间不同系数矩阵产生法的广义Fourier特征值谱分析结果
Fig.1 General-Fourier analysis of homogeneous half space for different grid matrix generations
表1 均匀半空间模型的广义Fourier谱分析对比结果
Table 1 General Fourier spectra analysis for half-homogenous model
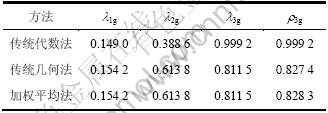
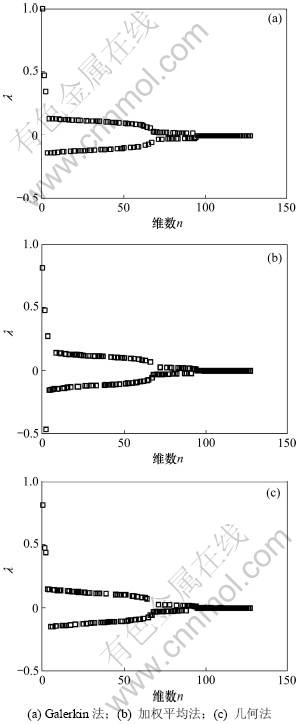
图2 3层模型不同系数矩阵产生法的广义Fourier特征值谱分析结果
Fig.2 General-Fourier analysis of homogeneous half space for different grid matrix generations
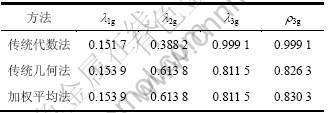
表2 3层模型的广义Fourier谱分析对比
Table 2 General Fourier spectra analysis for three-layer model
4.2 边界截取效果分析
这里利用多重网格法的特点对计算区域的边界进行压缩,使得计算区域减小。采用前面的均匀半空间模型和3层模型,利用从0.004~400 Hz的25个等对数间距的周期电磁波,以式(4)中的边界条件为基础,经过若干次多重网格法循环得到粗略的解;然后,截取想要的边界,将边界上的值作为新的边界条件,再以截取前的粗略计算结果作为初值进行多重网格法的循环求解。
对于均匀半空间模型,采用二重网格法进行求解,利用超松弛法进行平滑。截取边界前经过1次二重网格法循环,每次分别采用1次前预处理和后预处理。截取后采用4次二重网格法循环,每次循环分别采用2次前预处理和后预处理。图3显示频率为58.712 Hz时,截取前所求不同深度的电场强度。从图3可以看出:深部场的变化比较平滑,截取前在深部得到了能反映真实解的近似解,而浅部和空气中的解与真实解相差比较大。图4所示为对数坐标下边界被截取到不同深度时,不同频率的电场强度绝对值。当截取到1倍的趋附深度时,电场的绝对值与直接解法的结果(近似称之为理论值)吻合得较好。图5所示为被截取到不同深度时,不同频率的相位图。从图5可见:当截取至1.0~1.5倍的趋附深度时,相位与理论值偏差大;截取至1.8倍的趋附深度时,两者近似相等。在对数坐标下,不同频率的相位相对于理论值整体向下平移。图6所示为对频率为58.712 Hz的电磁波上边界进行截取后不同深度的电场强度计算结果。由于最终结果并不收敛到理论值,所以上边界的截取不可行。
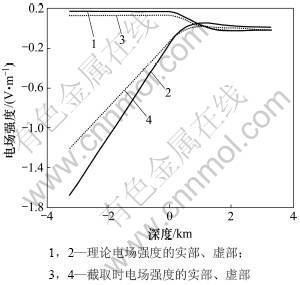
图3 均匀半空间模型不同深度电场的模拟结果
Fig.3 Electrical field modeling results of homogeneous half space for different depth
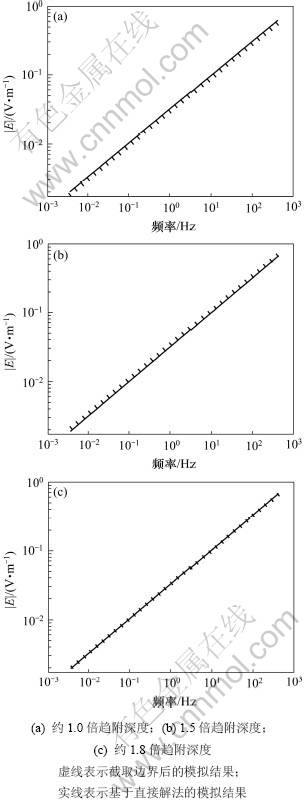
图4 均匀半空间电场的绝对值
Fig.4 Absolute value of electrical fields for homogeneous half space
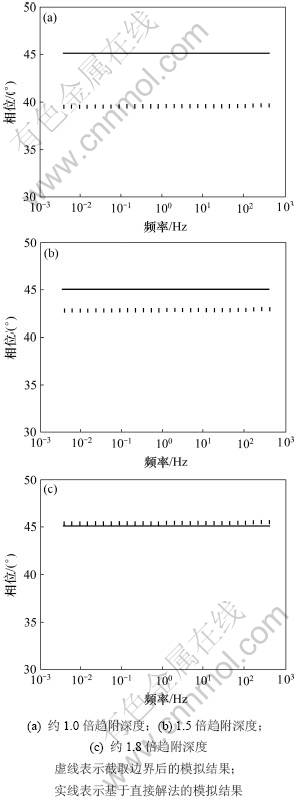
图5 均匀半空间的相位图
Fig.5 Phase diagram of electrical field for half space model with a boundary truncation
对于3层模型,采用三重V型网格法求解,超松弛法进行平滑。截取边界前经过2次三重网格法循环,每次分别采用2次前预处理和后预处理。截取后采用4次三重网格法循环,每次循环分别采用2次前预处理和后预处理。图7所示为截取到不同趋附深度时,电场强度绝对值随频率的变化图。从图7可以看出:当截取到0.3倍趋附深度时,截取边界后计算的电场强度与理论值偏差大,说明截取的边界条件不能近似实际的边界条件;当截取到2.0倍和3.4倍趋附深度时,截取边界后计算的电场强度与理论值比较吻合。图8所示为对应于图7的相位图。从图8可以看出:截取到0.3倍趋附深度时的相位与理论相位相差比较大;截取到2.0倍和3.4倍趋附深度的相位与理论相位接近。
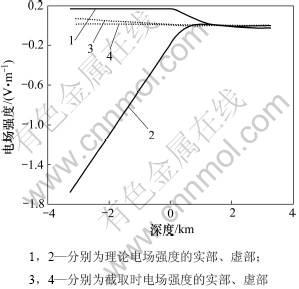
图6 不同深度电场的模拟结果
Fig.6 Electrical field modeling results for different depths
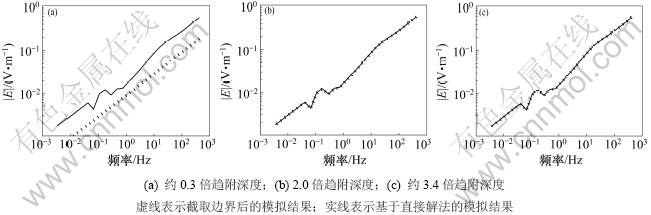
图7 3层模型的电场强度绝对值
Fig.7 Absolute value of electrical field for three-layer model with a boundary truncation
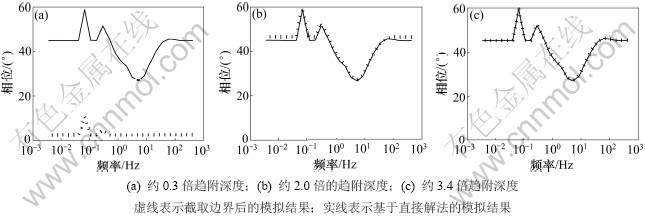
图8 3层模型电场相位图
Fig.8 Phase diagram of electrical field for three-layer model with a boundary truncation
5 结论
(1) 在粗化网格上,采用加权平均法产生粗网格近似。均匀半空间和3层模型分析结果显示加权平均法近似的渐近收敛性明显比Galerkin法(采用简单的插值矩阵)的好,但比传统的几何多重网格法略差。收敛性的广义Fourier谱分析在大地电磁法中对介质的非连续性不敏感,不能区分模型变化带来的收敛性变化。低重广义Fourier谱分析不能很好地反映多重网格法的收敛性。
(2) 在求解过程中,利用多重网格法的特点将粗网格上的解插值到边界上进行压缩,以减少计算区域加快收敛。随着边界截取的增加,满足特定收敛标准的数值解与理论解偏差就越大;当截取到约2.0倍的趋附深度时,截取后的计算结果(电场强度或相位)与理论值近似。在对数坐标下(或频率取对数下),当截取边界的值不能很好地近似该处的实际值时,计算的电场强度绝对值(或相位)尽量趋于理论值的整体 平移。
参考文献:
[1] Weaver J T, Brewitt-Taylor C R. Improved boundary conditions for the numerical solution of E-polarization problems in geomagnetic induction[J]. Geophysical Journal of the Royal Astronomical Society, 1978, 54(2): 309-317.
[2] Zhdanov M S, Golubev N G, Spichak V V, et al. The construction of effective methods for electromagnetic modeling[J]. Geophysical Journal of the Royal Astronomical Society, 1982, 68(3): 589-607.
[3] Zhdanov M S, Dmitriev V I, Fang S, et al. Quasi-analytical approximations and series in electromagnetic modeling[J]. Geophysics, 2000, 65(6): 1746-1757.
[4] Habashy T M, Groom R W, Spies B R. Beyond the Born and Rytov approximations: A nonlinear approach to electromagnetic scattering[J]. Journal of Geophysical Research, 1993, 98(B2): 1759-1775.
[5] Berenger J P. A perfectly matched layer for the absorption of the electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200.
[6] Turkel E, Yefet A. Absorbing PML boundary layers for wave-like equations[J]. Applied Numerical Mathematics, 1998, 27(4): 533-557.
[7] Engquist B, Majda A. Absorbing boundary conditions for the numerical simulation of waves[J]. Mathematics of Computation, 1977, 31(139): 629-651.
[8] Moore T G, Blaschak J G, Taflove A et al. Theory and application of radiation boundary operators[J]. IEEE Transactions on Antennas and Propagation, 1988, 36(12): 1797-1812.
[9] Mittra R, Ramahi O. Absorbing boundary conditions for the direct solution of partial differential equations arising in electromagnetic scattering problems[C]//Morgan M A. PIER2: finite element and finite difference methods in electromagnetic scattering. New York: E1sevier, 1990: 133-173.
[10] Chang S K, Mei K K. Application of the unimoment method to electromagnetic scattering of dielectric cylinders[J]. IEEE Transactions on Antennas and Propagation, 1976, 24(1): 35-42.
[11] Jin J M, Liepa V V. Application of hybrid finite element method to electromagnetic scattering from coated cylinders[J]. IEEE Transactions on Antennas and Propagation, 1988, 36(1): 51-54.
[12] Tzoulis A, Eibert T F. A hybrid FEBI-MLFMM-UTD method for numerical solutions of electromagnetic problems including arbitrarily shaped and electrically large objects[J]. IEEE Transactions on Antennas and Propagation, 2005, 53(10): 3358-3366.
[13] Hackbusch W. On the multi-grid method applied to difference equations[J]. Computing, 1978, 20(4): 291-306.
[14] Brandt A, McCormick S F, Ruge J. Algebraic multigrid (AMG) for automatic multigrid solution with application to geodetic computations[M]. Colorado: Institute for Computational Studies, 1982: 4-6.
[15] Bochev P B, Hu J J, Siefert C M, et al. An algebraic multigrid approach based on a compatible gauge reformulation of Maxwell’s equations[J]. Siam Journal on Scientific Computing, 2008, 31(3): 557-583.
[16] Brewitt-Taylor C R, Weaver J T. On the finite difference solution of two-dimensional induction problems[J]. Geophysical Journal of the Royal Astronomical Society, 1976, 47(2): 375-396.
[17] 柳建新, 降鹏飞, 童孝忠, 等. 不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用[J]. 中南大学学报: 自然版, 2009, 40(2): 485-491.
LIU Jian-xin, JIANG Peng-fei, TONG Xiao-zhong, et al. Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning to two-dimensional magnetotelluric forward modeling[J]. Journal of Central South University: Science and Technology, 2009, 40(2): 485-491.
[18] Fletcher R, Reeves C M. Function minimization by conjugate gradients[J]. Computer Journal, 1964, 7(2): 149-154.
[19] Elman H C, Ernst O G, O’Leary D P. A multigrid method enhanced by Krylov subspace iteration for discrete Helmholtz equations[J]. Siam Journal on Scientific Computing, 2001, 23(4): 1291-1315.
[20] Day D, Heroux M A. Solving complex-valued linear systems via equivalent real formulations[J]. Siam Journal on Scientific Computing, 2001, 23(2): 480-498.
[21] Wienands R, Oosterlee C W. On three-grid Fourier analysis for multigrid[J]. Siam Journal on Scientific Computing, 2001, 23(2): 651-671.
(编辑 陈灿华)
收稿日期:2010-11-21;修回日期:2011-03-08
基金项目:湖南省重大科技专项(2008FJ1006);教育部博士点基金资助项目(20070533102);有色金属资源与地质灾害探查湖南省重点实验室基金资助项目(2010994012-6)
通信作者:郭荣文(1981-),男,江西赣州人,博士研究生,从事地球物理正、反演理论研究;电话:13517493842;E-mail: rwguo@uvic.ca