DOI: 10.11817/j.issn.1672-7207.2017.12.025
基于Kriging时空统一模型的隧道动态施工位移预测
张可能1, 2,胡达1, 2, 3,何杰4,吴有平1, 2
(1. 中南大学 有色金属成矿预测与地质环境监测教育部重点实验室,湖南 长沙,410083;
2. 中南大学 地球科学与信息物理学院,湖南 长沙,410083;
3. 湖南联智桥隧技术有限公司,湖南 长沙,410200;
4. 湖南工业大学 科技学院,湖南 株洲,412007)
摘要:将经典的Kriging空间插值进行时空扩展,应用时空变异函数建立隧道围岩位移预测模型;分析参数与变形的之间的关系,给出时空插值的计算程序和方法。在此基础上采用时空统一Kriging插值预测模型和DGM(1,1)灰色预测模型预测隧道施工过程中掌子面前方一定范围内任意时刻的拱顶沉降。以湖南省娄底市笋安山隧道为试验对象,对比分析以上2个预测模型的位移预测值与实测值,并分别对位移预测值和实测值进行交叉验证。研究结果表明:相对于DGM(1,1)灰色预测模型,时空统一Kriging模型预测精度更高,能更准确地预测拱顶下沉位移的发展变化趋势,在实际隧道工程的围岩位移预测中是有效的、可行的。
关键词:Kriging模型;隧道工程;位移预测;灰色预测;掌子面
中图分类号:TU441 文献标志码:A 文章编号:1672-7207(2017)12-3328-07
Tunnel construction of dynamic displacement prediction based on unified space-time Kriging model
ZHANG Keneng1, 2, HU Da1, 2, 3, HE Jie4, WU Youping1, 2
(1. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environmental Monitoring,
Ministry of Education, Central South University, Changsha 410083, China;
2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;
3. Hunan Lianzhi Bridge & Tunnel Technology Co. Ltd., Changsha 410200, China;
4. College of Science and Technology, Hunan University of Technology, Zhuzhou 412007, China)
Abstract: The classical Kriging spatial interpolation was extended by space-time, and the displacement prediction model of tunnel surrounding rock was established by using spatiotemporal variation function. Base on the analysis of the relationship between parameters and displacement, the calculation procedure was given and method of temporal-spatial interpolation was put forward. Then Kriging interpolation prediction model with space-time unification and DGM(1,1) grey prediction model were applied to predict the vault displacement within a certain scope ahead of excavation face at any time during tunnel construction. Sunanshan Tunnel is located in Loudi City of Hunan Province, which was taken as the test subject to analyze displacement differences between the predicted values and the measured values of the above two prediction models, and the predicted values and measured values were cross-checked respectively. The results show that compared with the DGM(1,1) grey prediction model, the prediction accuracy of unified space-time Kriging model is higher, which shows that it can more accurately predict the trend of the vault settlement displacement and proves to be effective and feasible in displacement prediction of surrounding rock in actual tunnel project.
Key words: Kriging model; tunnel project; displacement prediction; grey prediction theory; tunnel face
隧道围岩位移预测预报是围岩稳定性研究中最重要的内容,尽管国内外学者在这方面已经积累了一些研究成果,但对位移预测的研究较少。隧道围岩位移预测预报对施工决策有特别重要的意义。在现场测试中,由于受测试条件、人员等各种可预见或不可预见的因素的影响,所获得的监测数据存在偶然误差和离散性。同时,仅仅依靠散点图无法实现对最终变形量的预测。在实际应用中,必须进行数学处理,获得能准确反映实际情况的典型曲线,找出量测位移随时间或空间变化的规律并预测量测位移的极值,同时预测其发展变化趋势,以科学地评价围岩和支护的稳定性、可靠性和经济合理性等。目前,最主要的预测方法有回归分析、时间序列分析法、经验公式法、灰色预测模型、人工神经网络模型、支持向量随机模型、数值分析等。Kriging插值法是一种运用结构分析与变异函数相关理论,在有限空间内针对区域化变量进行最优和无偏估值计算的预测方法。与上述传统预测方法相比,Kriging插值能更好地描述描述空间的连续关联性并反映数据点的整体变化趋势,预测更精确。尽管Kriging插值法在地质勘探和地质统计领域中应用较广泛,但在岩土工程领域应用较少,研究者主要进行Kriging法与其他学科应用交叉研究[1-7],如应用于可靠度理论、大气污染理论、灵敏度分析和降水量分析等领域。国内学者基于Kriging法在岩土工程领域也进行了大量有针对性研究,如应用Kriging方法研究边坡的变形速率、滑坡危险性区划、可靠度问题和单一时空的扩展方法等[8-15]。应用Kriging插值法进行隧道围岩的变形分析,可以得出隧道在动态施工过程中围岩位移的时空变化相关规律,进而基于这一规律进行隧道变形预测。为此,本文作者基于娄衡(湖南娄底—衡阳)高速公路笋安山隧道的现场监测数据和地质资料,引入时空统一Kriging预测模型对隧道施工过程中掌子面前方一定范围内任意时刻的拱顶下沉位移进行预测,并与灰色预测模型预测值进行对比研究,从整体上分析预测隧道围岩变形趋势,从而判断围岩的稳定性。
1 Kriging方法及DGM(1,1)灰色预测模型
1.1 Kriging基本理论
Kriging插值法的基本数学模型[6]为
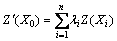 (1)
(1)
式中: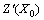 为预测点的估计值;Z(Xi)为预测点邻域内参与预测的参考点的值;λi为Kriging权系数,它是在无偏性和最小方差性的条件下,依据变异函数的计算结果而确定的。
为预测点的估计值;Z(Xi)为预测点邻域内参与预测的参考点的值;λi为Kriging权系数,它是在无偏性和最小方差性的条件下,依据变异函数的计算结果而确定的。
式(1)是n个数值的线性组合方程,Kriging方法的原则就是保证估计量是无偏的,且在估计方差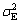 最小的前提下,求出n个权值系数λi。
最小的前提下,求出n个权值系数λi。
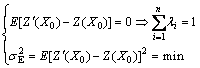 (2)
(2)
式中: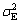 为估计方差。
为估计方差。
要在无偏性条件下,使估计方差最小。这是求条件极值的问题,采用拉格朗日乘子法予以解决。
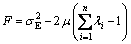 (3)
(3)
F是n个权系数和μ的(n +1)元函数,求出F 对权重系数λi和拉格朗日系数μ的偏导数,最后得到用半变异函数值表示的Kriging方程组[13]:
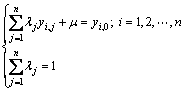 (4)
(4)
式中: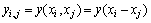 ;
;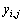 为半变异函数值。
为半变异函数值。
1.2 半变异函数理论模型
半变异函数或者半变差函数是从空间统计学中的方差概念演化而来[6,17],区域变量Z(x)在点x和x+h的值Z(x)和Z(x+h)之差的方差的1/2定义为区域变量Z(x)在x轴上的半变差函数,记为γ(h),即
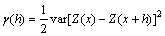 (5)
(5)
试验半变异函数计算公式为
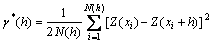 (6)
(6)
式中:N(h)为被增量h分隔的实验数据对的数目。
为了对区域化变量的未知值进行估计,需要将试验半变差函数拟合成相应的理论半变差函数模型[16-17]。传统Kriging算法提供的半变异函数模型有高斯模型、线形模型、球形模型、阻尼正弦模型和指数模型等。考虑到本文应用于隧道变形预测,选用球形模型,这样既考虑了储层参数的随机性,又考虑了储层参数的相关性。在满足插值方差最小的条件下,给出最佳线性无偏插值,同时还给出插值方差。具体模型表达式如下:
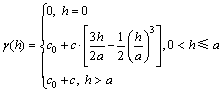 (7)
(7)
式中:c0为块金值;c0+c为基台值;c为偏基台值;a为变程;h为滞后距。
1.3 DGM(1,1)灰色预测模型
DGM(1,1)模型的基本形式如下:
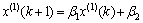 (8)
(8)
设非负序列
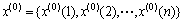 (9)
(9)
其1次累加形成的序列为
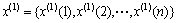 (10)
(10)
其中: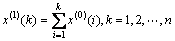 ;若
;若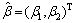 为参数列。令
为参数列。令
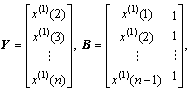
则灰色微分方程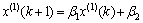 的最小二乘估计参数列满足:
的最小二乘估计参数列满足: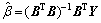 。
。
设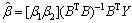 ,则取
,则取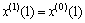 ,其预测模型为
,其预测模型为
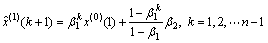 (11)
(11)
通过还原生成算法,得到预测函数:
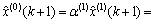
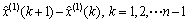 (12)
(12)
1.4 模型精度检验
均方根误差RMSE为
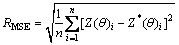 (13)
(13)
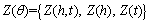 (14)
(14)
式中:Z*(θ)为估计值;Z(θ)为在相同点的观测值;n为估计点数量。
平均误差RE为
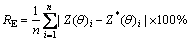 (15)
(15)
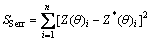
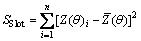
相关系数R2为
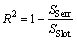 (16)
(16)
式中: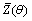 为样本平均值;
为样本平均值;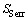 为残差平方和;
为残差平方和;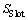 为总体平方和。
为总体平方和。
2 Kriging时空插值模型建模思想
2.1 空间插值
算法程序流程图设计见图1。

图1 程序设计流程图
Fig. 1 Program design flow chart
2.2 时空插值
空间Kriging只能估计某一时间上未知区域的变形量,若要估计任意时刻任意位置的变形量,则需要进行时空Kriging插值。在隧道掘进过程中,监测点的布置、数据的采集以及位移的变化不仅仅是单纯空间和时间上的变化,而是时间与空间的统一。本文选用普通Kriging方法实现数据的时空插值[17-18],计算公式如下:
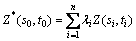 (17)
(17)
式中: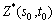 为时空点
为时空点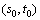 处的估计值;λi为临近观测值
处的估计值;λi为临近观测值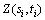 的加权系数。引入拉格朗日系数μ进行推导可得
的加权系数。引入拉格朗日系数μ进行推导可得
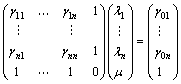 (18)
(18)
式(18)中的加权系数λ可通过式(1)得到,代入式(17)可得研究区域内任意点的插值估计。
在隧道工程实际监控量测作业中采集到的时间序列数据一般都是非等间距的,隧道围岩变形阶段不同,量测频率也不同。因此,应用回归模型、灰色模型、人工神经网络模型等方法对量测数据进行分析处理时,除非按照试验研究方案按时量测,否则必须先采用数学方法,将这类非等距的时间序列变换成等距的时间序列数据,再进行下一步分析。应用时空Kriging插值预测模型能很好地解决这一问题,可以避免依次考虑隧道中每个因素所造成的影响,而分析各影响因素之间的相关性,并且能提高预测精度。
为了简化时空Kriging插值预测模型计算过程,假设:1) 隧道变形监测位移是隧道围岩形变规律的宏观体现,其变形分析的预测值仅对围岩形变规律进行深度数据挖掘;2) 隧道围岩在动态施工过程中最终产生的应力应变是受地质体内外界条件与各种因素的相互影响、综合作用的结果;3) 隧道围岩各影响因素间相互作用、相互影响且呈现非线性规律,但能够组建隧道变形分析预测模型对其进行拟合处理。
3 工程概况
笋安山隧道位于双峰县与衡阳县交界的笋安山,起讫桩号为左洞ZK31+800~ZK35+340,右洞YK31+800~YK35+370,左洞长3 540 m,右洞长3 570 m,属特长隧道。本隧道为双洞单向交通隧道,左右洞测设线间距为23.69~41.88 m,两端属于小净距隧道,中间段属于分离式隧道。目前,该隧道采用新奥法进行施工。该隧道场地地貌类型为低山丘陵地貌,地表剥蚀较强烈,隧道山顶最大高程为444.00 m。隧道主要岩性为第四系残坡积层、奥陶系上统(O3)石英砂岩、板岩和泥盆系中统(D2t)跳马涧组钙质砂岩。试验区是娄衡高速公路笋安山隧道典型监测断面,监测区为右线YK31+860-880。该段监测区域为进口浅埋段,围岩主要为黏性土夹碎石呈松散破碎状,基本上无自稳能力。由于该段围岩拱顶下沉沉降量较大,大大超出设计预留沉降量且拱顶喷射混凝土局部有开裂现象,故拱顶沉降监测点间距均加密设置为3 m。取YK31+863,YK31+866和YK31+869这3个断面的拱顶沉降位移为基础实验数据,从同一天开始观测,并每天在同一时间持续观测34 d;分别取掌子面前方YK31+872,YK31+875和YK31+878这3个断面34 d的拱顶沉降观测位移作为试验验证数据。
4 预测与分析
将上述现场试验位移分成3组分步导入Kriging时空模型进行计算。
第1组:以YK31+863,YK31+866和YK31+869这3个断面34 d的监测点数据预测前方YK31+872断面监测点34 d内的拱顶沉降。
第2组:以YK31+866,YK31+869和YK31+872这3个断面34 d的监测点数据为基础预测前方YK31+875断面监测点34 d内的拱顶沉降位移。
第3组:以YK31+869,YK31+872,YK31+875这3个断面34 d的监测点数据为基础预测前方YK31+878断面监测点34 d内的拱顶沉降位移。
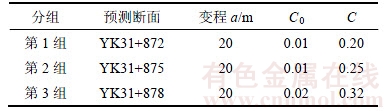
每组计算采用的半变异函数相关参数如表1所示。为了进一步验证Kriging时空模型的合理、有效性,采用DGM(1,1)灰色预测模型预测结果与Kriging时空模型预测结果进行对比。
表1 空间变异函数参数
Table 1 Parameters of spatial variograms function
DGM(1,1)灰色预测模型预测采用YK31+872,YK31+875和YK31+878这3个断面处的拱顶下沉值为基础试验数据。由式(8)~(12)建立灰色预测模型,可计算得到如下相应的时间响应函数。
1) YK31+872拱顶沉降时间响应函数为
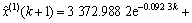
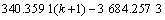 ;
;
k=1,2,…,n-1。 (19)
2) YK31+875拱顶沉降时间响应函数为
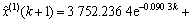
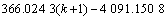 ;
;
k=1,2,…,n-1。 (20)
3) YK31+878拱顶沉降时间响应函数为
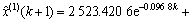
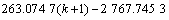 ;
;
k=1,2,…,n-1。 (21)
由式(19)~(21)可计算得出变形预测值。
计算结果及成果图如图2~7所示。
预测结果是否符合实际,应该进行交叉验证,并对本预测模型进行检验评价。本文根据式(13)~(16),用残差由均方根公式计算出预测误差(RMSE),进而求出平均误差(RE)。将以上指标作为检验标准检验预测效果的有效性,检验标准值越小则反映预测结果越准确,预测值也就越接近真实值;平均误差趋于“0”认为估计是无偏的;计算相关系数R2,其值越接近“1”,表明预测曲线与实测曲线的线性相关程度越高。
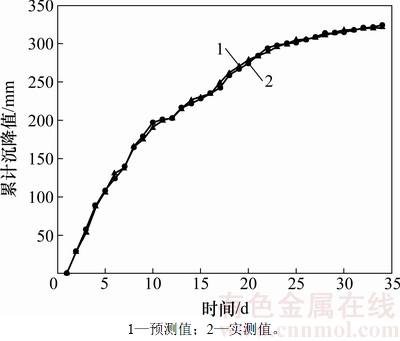
图2 YK31+872拱顶沉降实测值与Kriging预测值对比
Fig. 2 Crown settlement measured values compared with the predicted values of Kriging for YK31+872
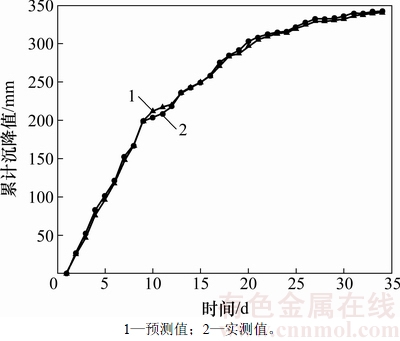
图3 YK31+875拱顶沉降实测值与Kriging预测值对比
Fig. 3 Crown settlement measured values compared with the predicted values of Kriging for YK31+875
由本文所述的Kriging时空统一插值模型和DGM(1,1)灰色预测模型得到的3个预测值精度评价指标,如表2所示。从表2可见:Kriging模型的均方根最小误差为3.106 0,最小平均误差为0.043 2,相关系数均接近1.000 0;而灰色预测模型的均方根最小误差为8.980 0,最小平均误差为7.211 0,相关系数均接近1.000 0。从而证明了Kriging时空统一预测模型相比灰色预测模型具有更高的预测精度,也表明其在实际工程的运用过程中具有更高精度的可行性和有效性。
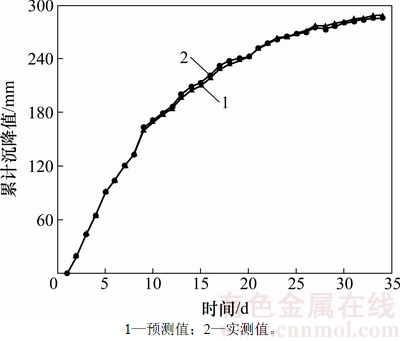
图4 YK31+878拱顶沉降实测值与Kriging预测值对比
Fig. 4 Crown settlement measured values compared with the predicted values of Kriging for YK31+878
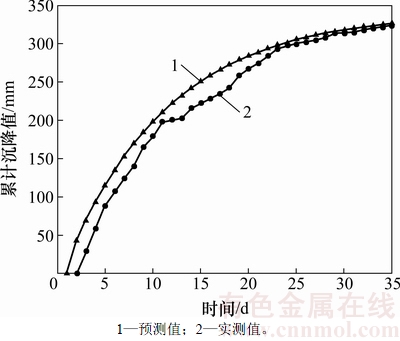
图5 YK31+872拱顶沉降实测值与灰色预测值对比
Fig. 5 Crown settlement measured values compared with grey predicted values for YK31+872
表2 精度评价指标
Table 2 Precision evaluation

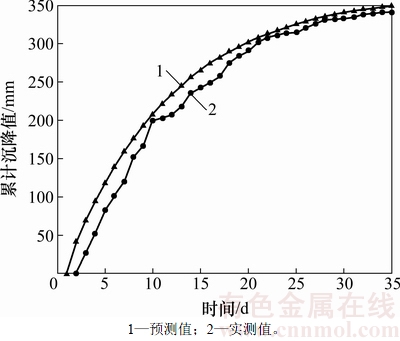
图6 YK31+875拱顶沉降实测值与灰色预测值对比
Fig. 6 Crown settlement measured values compared with grey predicted values for YK31+875
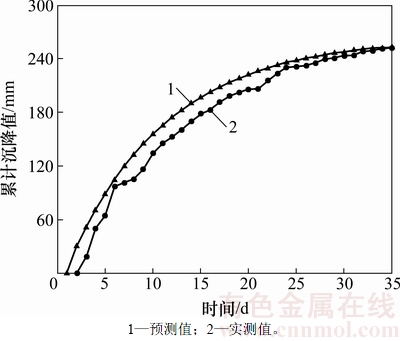
图7 YK31+878拱顶沉降实测值与灰色预测值对比
Fig. 7 Crown settlement measured values compared with grey predicted values for YK31+878
5 结论
1) 在隧道变形预测中引入时空统一Kriging预测模型,应用时空变异函数建立了隧道围岩位移预测模型。并针对隧道施工过程中拱顶下沉位移的实测值分别运用时空统一Kriging预测模型、DGM(1,1)灰色预测模型这2种模型进行分析预测,分析对比实测与预测位移-时间曲线之间的关系。
2) 通过交叉验证和相关精度指标对时空统一Kriging预测模型、DGM(1,1)灰色预测模型这2种模型进行对比评定,证明了时空统一Kriging预测模型具有较高的预测精度和可靠性,能更好地反映隧道围岩形变的变化趋势,为隧道工程监测预报技术提供了一种全新的研究手段。
3) Kriging预测模型估计值具有不确定与无规律性,不能完整地揭示围岩内部变形的信息。因此,应当进一步结合灰色预测等相关数学方法对其进行深度挖掘和改进,以提高预测精度和效率。
参考文献:
[1] MYERS D E. Kriging, cokriging, radial basis functions and the role of positive definiteness[J]. Computers & Mathematics with Applications, 1992, 24(12): 139-148.
[2] TAYLOR J A, JAKEMAN A J, SIMPSON R W. Modeling distributions of air pollutant concentrations. Ⅰ. Identification of statistical models[J]. Atmospheric Environment, 1986, 20(9): 1781-1789.
[3] BARTHELEMY J F M, SOBIESZCZANSKI S J. Optimum sensitivity derivatives of objective function in non-liner programming[J]. AIAA Journal, 1983, 21(6): 913-915.
[4] ALEXANDROV N M, MICHAEL L R. Analytical and computational aspects of collaborative optimization[R]. Hampton, USA: NASA Langley Technical Report Server, 2000: 145-158.
[5] TRAUTH M, SILLMANN E. MATLAB and design recipes for earth sciences[M]. Heidelberg, Berlin: Springer, 2013.
and design recipes for earth sciences[M]. Heidelberg, Berlin: Springer, 2013.
[6] KODIYALAM S. Evaluation of methods for multidisciplinary design optimization(MDO): Phase I[R]. Hampton, USA: NASA Langley Technical Report Server, 1998: 259-272.
[7] JAROSLAW S, AGTE J S, SANDUSKY J R R. Bi-level integrated system synthesis (BLISS)[R]. Hampton, USA: NASA Langley Technical Report Server, 1998: 348-361.
[8] 陶月赞. 动态Kriging 方法[J]. 世界地质, 1997, 16(4): 56-58.
TAO Yuezan. Dynamic Kriging method[J]. Global Geology, 1997, 16(4): 56-58.
[9] 周小文, 付晖, 吴昌瑜. 地层特性随机场插值方法应用研究[J]. 岩土力学, 2005, 26(2): 221-224.
ZHOU Xiaowen, FU Hui, WU Changyu. Application study of spatial interpolation method in geological random field[J]. Rock and Soil Mechanics, 2005, 26(2): 221-224.
[10] 岳建平, 甄宗坤. 基于粒子群算法的 Kriging插值在区域地面沉降中的应用[J]. 测绘通报, 2012, 31(3): 59-62.
YUE Jianping, ZHEN Zongkun. Application of particle swarm optimization based Kriging interpolation method in regional land subsidence[J]. Bulletin of Surveying and Mapping, 2012, 31(3): 59-62.
[11] 熊勇刚, 田万鹏, 陈科良, 等. 基于 Kriging 插值无网格法的动力弹塑性分析[J]. 中南大学学报(自然科学版), 2014, 45(2): 435-440.
XIONG Yonggang, TIAN Wanpeng, CHEN Keliang, et al. Dynamic elastoplastic analysis by using meshless Kriging interpolation method[J]. Journal of Central South University (Science and Technology), 2014, 45(2): 435-440.
[12] 刘志平, 何秀凤, 张淑辉. 多测度加权克里金法在高边坡变形稳定性分析中的应用[J]. 水利学报, 2009, 40(6): 709-716.
LIU Zhiping, HE Xiufeng, ZHANG Shuhui. Multi-distance measures weighted Kriging method for deformation stability analysis of steep slopes[J]. Journal of Hydraulic Engineering, 2009, 40(6): 709-716.
[13] 朱吉祥, 张礼中, 周小元, 等. Kriging法在区域滑坡危险性评价中的应用[J]. 水文地质工程地质, 2012, 39(3): 114-118.
ZHU Jixiang, ZHANG Lizhong, ZHOU Xiaoyuan, et al. Application of Kriging to the assessment of regional landslide hazards[J]. Hydrogeology & Engineering Geology, 2012, 39(3): 114-118.
[14] 王建民, 张锦, 邓增兵, 等. 时空Kriging插值在边坡变形监测中的应用[J]. 煤炭学报, 2014, 39(5): 874-879.
WANG Jianmin, ZHANG Jin, DENG Zengbing, et al. Slope deformation analyses with space-time Kriging interpolation method[J]. Journal of China Coal Society, 2014, 39(5): 874-879.
[15] 李晓军, 王长虹, 朱合华. Kriging 插值方法在地层模型生成中的应用[J]. 岩土力学, 2009, 30(1): 157-162.
LI Xiaojun, WANG Changhong, ZHU Hehua. Kriging interpolation and its application to generating stratum model[J]. Rock and Soil Mechanics, 2009, 30(1): 157-162.
[16] KYRIAKIDIS P C, JOURNEL A G. Geostatistical space–time models: a review[J]. Mathematical Geology, 1999, 31(6): 651-684.
[17] 吴学文, 晏路明. 普通Kriging法的参数设置及变异函数模型选择方法[J]. 地球信息科学学报, 2007, 9(3): 104-109.
WU Xuewen, YAN Luming. Setting parameters and choosing opti-mum semivariogram models of ordinary Kriging interpolation[J]. Journal of Geo-Information Science, 2007, 9(3): 104-109.
[18] 徐爱萍, 胡力, 舒红. 空间克里金插值的时空扩展与实现[J]. 计算机应用, 2011, 31(1): 273-276.
XU Aiping, HU Li, SHU Hong. Extension and implementation from spatial-only to spatio temporal Kriging interpolation[J]. Journal of Computer Applications, 2011, 31(1): 273-276.
(编辑 陈灿华)
收稿日期:2016-12-15;修回日期:2017-03-12
基金项目(Foundation item):国家自然科学基金资助项目(51108176)(Project(51108176) supported by the National Natural Science Foundation of China)
通信作者:胡达,博士研究生,工程师,从事岩土工程研究;E-mail:huda-2005@163.com