Evaluation of stress intensity factors of thin AZ31B magnesium alloy

plate under biaxial tensile loading

WANG Jian-gang(王建刚)¹, ZHAO Hong-yang(赵红阳)², JU Dong-ying(巨东英)^{2, 3}

1. Graduate School, Saitama Institute of Technology, Fusaiji 1690, Fukaya, Saitama 369-0293, Japan;

2. Department of Material Science and Engineering, University of Science and Technology Liaoning,

Anshan 114051, China;

3. Department of Material Science and Engineering, Saitama Institute of Technology,

Fusaiji 1690, Fukaya, Saitama 369-0293, Japan

Received 23 September 2009; accepted 30 January 2010

Abstract: Stress intensity factors of thin AZ31B magnesium alloy sheet under biaxial tension loading were analyzed by modified Dugdale model. K-values with crack angle of 90? obviously show that there is no influence of the loading condition in Mode-I. In the 45? case, K_Ⅰ values are obtained within 10% errors when they are calculated by modified Dugdale model under biaxial loading. It is concluded that the modified Dugdale model is one of effective ways to evaluate stress intensity factor of AZ31 magnesium alloy sheet appropriately.

Key words: Mg alloy; plate; cross-rolling; isotropic material; biaxial tension; stress intensity factor

1 Introduction

In recent years, innovations of new materials allow machines and structures to become bigger, lighter, and faster, and this trend is still continuing. For example, auto industry is driven to use the light weight and strong materials in order to improve fuel consumption efficiency of vehicle and reduce CO₂ emissions. The superplastic forming can effectively produce complex engineering components directly from wrought products in experimental level[1-5]. This forming is a viable technique to fabricate a hard-to-form material into complex shapes. In order to enhance the engineering applications in magnesium alloys, vertical twin roll casting and cross-rolling technology of magnesium sheet has been developed to obtain both less thickness and better quality sheet[6-9]. However, in order to be actually applied as a structural material, it is required to have sufficient mechanical properties to meet both reliability and safety. Concerning the mechanical property, the magnesium alloy sheet by twin roll casting and cross-rolling has been studied by some researchers and some achievements have been reached[10]. In fact, there is a little data, for example stress intensity factor, that can be used to evaluate the performances such as reliability and safety of magnesium alloys[11-12]. There are few reports about stress intensity factor of wrought magnesium alloys under complex load. Therefore, in this study, fracture experiments are conducted on the magnesium alloy under equitable biaxial stress and inequitable biaxial stress by using the miniature biaxial tensile test machine. Fractures are observed by the optical microscope. The stress is determined by Micro part X-ray stress measurement. Then, they are compared and analyzed with the stress intensity factor and the fracture toughness value. The stress intensity factor under biaxial loading condition using the cross-rolled magnesium alloys sheets (AZ31B) is investigated.

2 Experimental

2.1 Material and cross-rolling

The sample material used for the actual experiment is AZ31B magnesium alloy sheet by cross-rolling method. The schematic diagram of cross-rolling is shown in Fig.1. The materials were annealed at 673 K for 60 min. The microstructures were observed by optical microscopy (OM), as shown in Fig.2. It is obvious that anisotropy was negligible in the cross rolling experiments.

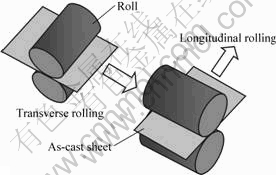
Fig.1 Schematic diagram of cross-rolling

Fig.2 Microstructure of annealed specimen

The alloy was received in the form of rolled sheet with a thickness of 0.5 mm.

Table 1 shows the chemical constitution of AZ31B magnesium alloy sheet. In order to examine the mechanical properties of each sample, the tensile tests were carried out at a speed of 0.01 mm/s and at room temperature. The tensile specimen that was machined directly from the rolled sheet after annealing had tensile axes of three angles (0?, 45? and 90?) to the rolled direction. The gauge length and the width were 26 mm and 10 mm, respectively. The yield strength, ultimate tensile strength, elastic medulus, Poisson ratio and elongation are listed in Table 2.

Table 1 Chemical constitution of AZ31B magnesium alloy (mass fraction, %)

Table 2 Mechanical properties of AZ31B magnesium alloy

2.2 Test specimens and experimental method

Fig.3 shows the size of the specimen. For the biaxial loading specimen, a hole was created by end mill with  1 mm in diameter. Then, the both sides of crack tips were processed to have the curvatures with 0.15 mm in radius. As a finish, the specimen in cross type of 50 mm in length and width, 10 mm in the width of the chuck, and 1.8 mm in a fillet radius was processed by a wire cutting machine. The thickness of the specimen plate was 0.5 mm. The rolling direction of the magnesium alloy strip was defined as y axis. Two angle values (φ=45? and 90?, φ is the angle between crack and rolling direction) were chosen.

Fig.3 Sample dimensions in tensile test

The experimental device used in this study is a miniature biaxial tensile test device which was developed by Ju-Lab in Saitama Institute of Technology, Japan. To in situ measure the deformation and the stress of crack tip, the optical microscopy and Micro part X-ray stress measurement were used. Table 3 lists the detailed X-ray stress measurement conditions. The load ratios (x axial? y axial) are 1?3, 1?2 and 1?1. The strain rate was 1.5×10^-3 s^-1. Three points (no load, loading in elastic and plastic region) were chosen. Fig.4 shows a typical micrograph of a crack in the AZ31B magnesium alloy sheet. In order to achieve high quality micrographs, the side surfaces of the specimen were polished before the test. From the

Fig.4 Extended process of crack and measuring point of residual stress

Table 3 X-ray stress measurement conditions

micrograph, opening displacement and plastic zone at two directions could be measured.

3 Fundamental theories

In the case of long, slender plastic zone at the crack tip in a non-hardening material under plane stress, the Dugdale model proposed the extent of the plastic zone, just as shown in Fig.5(a). The yield plastic zone of the strip was modeled by assuming a crack with length of 2a+2ω, where ω is the length of the plastic zone, a is the length of crack, with a closure stress of σ_{s, y} applied at each crack tip, as shown in Fig.5(a). The size of plastic zone ω was chosen such that the stress singularity vanishes at the end of the effective crack, that is, K_σ+K_ω=0. In case of σ <<σ_{s, y} and ω<

                                (1)

And due to the plastic deformation at crack tip, the sharp crack tip of the original point would become blunt (otherwise stress singularity will exist), which would result in a phenomenon that finite radius at the tip of the

Fig.5 Dugdale and modified Dugdale models: (a) Dugdale model; (b) Modified Dugdale model

initial crack opens up. A similar estimation can be obtained from the strip yield model:

                               (2)

where δ is the crack tip opening displacement (CTOD), σ_{s, y} is the yield stress of y axial, and G is the shear elastic modulus. CTOD and Dugdale model have been applied widely under uniaxial loading[13-16]. But it was not a credible exploration confirming method for plastic zone and crack tip opening deformation in loading process. In actual engineering, material works under multiaxial stress state. Therefore, it is important to consider coupling effect between K_Ⅰ and K_Ⅱ (K_Ⅰ and  K_Ⅱ, stress intensity factor of Mode-Ⅰ and Mode-Ⅱ). A modified Dugdale model in view of the coupled effect at crack tip was put forward during the open displacement of crack tip extended early stage, as shown in Fig.5(b). According to the coupling effect between K_Ⅰ and K_Ⅱ, the modified project is given by Eq.(3) and Eq.(4). Based on Eqs.(5) and (6), the stress intensity factor K_Ⅰ and K_Ⅱ can be obtained:

                     (3)

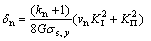                     (4)

where K_Ⅰ and K_Ⅱ can be written as

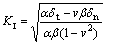                         (5)

                         (6)

where v is Poisson ratio. On isotropic condition, for plane stress, k_t=k_n=(3-v)/(1+v)[17], v_t=v_n, α=β=(k+1)/ 8Gσ_{s, y}.

Similarly, the relationship between plastic zone size and stress intensity factor can be obtained with the modified Dugdale model.

4 Results and discussion

4.1 Deformation of crack tip and stress distribution

Examples of the deformation of crack tip image by the optical microscope are shown in Fig.6. It is crack angle of 45? under biaxial stress that takes mixed mode of Mode-Ⅰ and Mode-Ⅱ, in case of the biaxial tension examination of the material because of the stress of crack tip by Micro part X-ray stress measurement device. In the 90? case, it is verified that the material under biaxial stress shows only Mode-Ⅰ. The appearance where the optical image grows as loading increases about all the notch opening displacement can be confirmed. In the optical image obtained from the biaxial tensile test, the plastic zone and microcrack near the tip of notch appear clearly and extend along the direction of 45? at the end stage of tensile test. It is suggested that the fracture of this alloy at room temperature is brittle fracture under biaxial tensile test.

Fig.6 In situ tensile photos of samples with different loading ratios in three load regions at 45? case

Moreover, the relation between the strain and stress obtained with the Micro part X-ray stress measurement device is shown in Fig.7. The results show that the stress near crack tip increases with the tensile testing. This tendency does not depend on crack angle and applied load. From Fig.7 and summarized results in Table 4, the stress values under biaxial loading test are higher than those under uniaxial loading test.

Table 4 Stress of samples in various loading region under both loading conditions

4.2 Evaluation of stress intensity factor under biaxial stress

The stress intensity factor (K_Ⅰ) for Mode-Ⅰ was

Fig.7 Relationship between loading condition and stress: (a) 90? case; (b) 45? case

calculated by the modified Dugdale model, as shown in Fig.8. This suggests that the K_Ⅰ takes low value at the early stage of tensile test, and the changing trend of K_Ⅰ value slows down at the end stage of test. Fig.9 shows

Fig.8 Relationship between loading condition and stress intensity factor: (a) 90? case; (b) 45? case

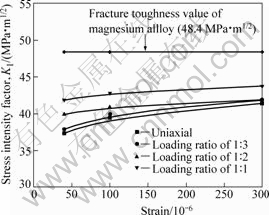
Fig.9 Comparison between calculated K_Ⅰ by Dugdale model and fracture toughness value in 45? case

the relationships between the fracture toughness value and the stress intensity factor for Mode-Ⅰ by Dugdale model in the 45? case. The K_Ⅰ value on the crack angle 45? by Dugdale model is 9%-20% lower than that of the fracture toughness value. This is because the coupling effect between Mode-Ⅰ and Mode-Ⅱ is neglected in the 45? case when it is conducted under biaxial loading test. As shown in Fig.10, it is found that the K_Ⅰ values are obtained within 10% errors when they are calculated by the modified Dugdale model under biaxial loading, but the errors are still large under uniaxial loading. From these results, it is confirmed that the analysis based on the modified Dugdale model is one of effective ways to evaluate stress intensity factor for AZ31B magnesium alloy sheet under biaxial stress. However, it is known that measurements (K_Ⅰ value) under the loading condition of corresponding practical use are required. Fig.11 shows the comparison between the calculated K_Ⅱ by the modified Dugdale model and the fracture toughness value. From Figs.10 and 11, it is found that Mode-I makes the main function under high loading ratio (1?1). The material under uniaxial loading condition shows mainly Mode-Ⅱ. Therefore, the coupling effect of Mode-Ⅰand Mode-Ⅱ under complex loading condition has important significance for the engineering applications of AZ31B magnesium alloy sheet.

Fig.10 Comparison between calculated K_Ⅰ by modified Dugdale model and fracture toughness value in 45? case

Fig.11 Comparison between calculated K_Ⅱ by modified Dugdale model and fracture toughness value in 45? case

From these results, it is found that the difference of K_Ⅰ value of this wrought AZ31B magnesium alloy with different loading ratios is 1-3 MPa?m^1/2. It is considered that the difference of the stress intensity factor is related to the deformation of the different tension directions. So, the stress intensity factor is related to the rolling process. Therefore, in the future, it is necessary to investigate the relationships between stress intensity factor and rolling process.

5 Conclusions

1) Under the biaxial tensile stress, the K_Ⅰ value with crack angle of 45? shows mixed mode of Mode-Ⅰ and Ⅱ, but the K_Ⅰ value shows only Mode-I in the 90? case.

2) The tolerance of stress intensity factor (K_Ⅰ value) by Dugdale model under the biaxial tension stress is reduced to 1%-8% by the modified model, and the effectiveness in the practical use of the stress intensity factor calculated by the modified Dugdale model under biaxial stress is confirmed. The effectiveness of application of the modified Dugdale model in the calculation of stress intensity factor under biaxial stress is thus clarified.

3) The tolerance of stress intensity factor (K_Ⅰ and  K_Ⅱ values) with different loading ratios is 1-4 MPa?m^1/2. The changes in these values are considered to depend on the deformation of different tension directions. This indicates the possibility of a new alloy design that has a high resistance to fracture by controlling rolling process. It is expected that higher stress intensity factor of AZ31B magnesium alloys is achieved by controlling rolling process and is able to enhance the engineering applications in the wrought magnesium alloys as well as to obtain their reliability and safety.

Acknowledgments

This research is partially supported by Open Research Center in Saitama Institute of Technology, Japan, and University of Science and Technology Liaoning, China.

References

[1] JU Dong-ying, HU Xiao-dong, ZHAO Hong-yang. Inelastic behavior and numerical analysis in twin-roll casting process of AZ31 alloy [J]. Arch Mech, 2009, 61: 229-239.

[2] WATANABE H, MUKAI T, HIGASHI K. High-strain-rate superplasticity in an AZ91 magnesium alloy processed by ingot metallurgy route [J]. Mater Trans, 2002, 43: 78-80.

[3] HU Xiao-dong. Studies on strip casting and rolling of magnesium alloy thin strip [D]. Fukaya: Saitama Institute of Technology, 2007: 99-112.

[4] SOMEKAWA H, HOSOKAWA H, WATANABE H, HIGASHI K. Diffusion bonding in superplastic magnesium alloys [J]. Mater Sci Eng A, 2003, 339: 328-333.

[5] KIM W J, CHUNG S W, CHUNG C S, KUM D. Superplasticity in thin magnesium alloy sheets and deformation mechanism maps for magnesium alloys at elevated temperatures [J]. Acta Metall, 2001, 49: 3337-3344.

[6] JU Dong-ying, ZHAO Hong-yang, HU Xiao-dong, KOICHI O, MITUO T. Thermal flow simulation on twin roll casting process for thin strip production of magnesium alloy [J]. Mater Sci Forum, 2005, 488/489: 439-444.

[7] HU Xiao-dong, JU Dong-ying. Application of Anand’s constitutive model on twin roll casting process of AZ31 magnesium alloy [J]. Trans Nonferrous Met Soc China, 2006, 16: s586-s590.

[8] HU Xiao-dong, JU Dong-ying, ZHAO Hong-yang. Thermal flow simulation and concave type slot nozzle design for twin roll casting of magnesium alloy AZ31 [J]. Mater Sci Forum, 2007, 539/543: 5037-5042.

[9] JU Dong-ying, HU Xiao-dong. Effect of casting parameters and deformation on microstructure evolution of twin-roll casting magnesium alloy AZ31 [J]. Trans Nonferrous Met Soc China, 2006, 16: s874-s877.

[10] KIM K H, LEE J G, BAE G T, BAE J H, KIMN J. Mechanical properties and microstructure of twin-roll cast Mg-Zn-Y alloy [J]. Mater Trans, 2008,49:980-985.

[11] SASAKI H, ADACHI M, TAKIMOTO A. Effect of microstructure on fracture toughness of AZ91 magnesium alloy [J]. JSME (A), 1996, 62: 1806-1812.

[12] REGENER D, DIETZE G, HEYSE H. Fracture toughness of pressure die cast magnesium alloys [J]. Materialwiss Werkst, 2002, 33: 606-613.

[13] NEIMITZ A. Modification of Dugdale model to include the work hardening and in- and out-of-plane constraints [J]. Eng Fract Mech, 2004, 71: 1585-1600.

[14] INHOY G U. Maximum-load predictions in the Dugdale model using a critical CTOA criterion [J]. J Test Eval, 1993, 21: 461-469.

[15] MOU Y H, HANR P S. Damage zones based on Dugdale model for materials [J]. Int J Fract, 1994, 68: 245-259.

[16] HOFFMAN R D, RICHMOND O. Application of the Dugdale model to crazing and fracture in rubber-modified polystyrene [J].J Appl Phys, 1976, 47: 4289-4294.

(Edited by YANG Bing)

Corresponding author: JU Dong-ying; Tel: +81-48-585-6826; Fax: +81-48-585-5928; E-mail: dyju@sit.ac.jp

DOI: 10.1016/S1003-6326(09)60291-0