自然通风动态风速条件建模

王亮，谭洪卫，季亮

(同济大学 机械与能源工程学院，上海，200092)

摘要：基于双参数Weibull模型、马尔科夫链模型及极大似然理论模型提出适用于自然通风的动态风速条件建模方法，并对方法的合理性进行阐述。与其他风速构造方法相比，构造序列时间间隔更小,可基于逐时数据进行构造；构造过程中同时考虑自然风速的统计特性及时序特性，风速特性反映更为全面。以上海地区风速为例，进行应用分析，并建立统计模型参数与逐时平均风速的回归模型及风速变化转移概率矩阵。通过与实测风速序列对比，对该方法的有效性进行验证。研究结果表明：反演风速序列与实测风速序列特性参数一致，其中整体序列统计模型拟合尺寸因子参数分别为实测序列为3.27相应反演序列为3.33，形状因子参数值分别为实测序列为2.26相应反演序列为2.28，其他参数相对偏差亦在5%之内，证明了该方法的有效性。

关键词：动态风速；马尔科夫链；自然通风；Weibull模型

中图分类号：P425.1          文献标志码：A         文章编号：1672-7207(2014)06-2071-07

Natural ventilation dynamic wind speed condition modeling

WANG Liang, TAN Hongwei, JI Liang

(School of Mechanical Engineering, Tongji University, Shanghai 200092, China)

Abstract: The dynamic wind speed modeling method was proposed based on two-parameter Weibull model, Markov chain and maximum likelihood method. And the rationality of the method was stated. Based on hourly wind speed, smaller time scale was considered and the statistical and temporal property were considered during the process of modeling. The application of the method was analyzed by taking Shanghan’s wind speeds as an example. The progression model of wind speed statistic model parameters and hourly wind speed were set up. And the matrix of transition probability was solved based on measuring data using automatic weather station. The validity of the method was testified by comparing inversion series wind speeds and measured values. The results show that the inversion series wind speeds matches the measured data. The fitting size coefficient is 3.27 for measured data and 3.33 for inversion data; the fitting size coefficient is 2.26 for measure data and 2.28 for inversion data. The other parameter relative deviation is within 5%.

Key words: dynamic wind; Markov chain; natural ventilation; Weibull model

随着全球对建筑节能技术的重视，自然通风作为一项重要的节能技术得到了重点关注。自然通风的驱动力为热压及风压。国内外学者已对自然通风进行了大量的研究并取得了许多成果。而大多数研究将自然风速条件设定为平均风速的恒定条件。该设置方法忽略了实际自然风风速变动特性对通风效果的影响，可能导致研究结果偏离客观事实^[1]，因此，必须考虑自然风风速的动态变化对自然通风效果的影响。通常自然通风评价用风速风向数据来源于当地气象台站，或当地典型气象年数据等气象资料。获取的风速风向条件最小时间间隔为1 h，而自然通风小时换气次数可达几次甚至十几次，时间间隔对于自然通风而言偏大^[2-4]，采用逐时恒定风速条件难以客观评价自然通风的效果，因此，更小时间间隔的动态风速数据对于合理、客观评价自然通风效果尤为重要。然而，更小尺度间隔的动态风速条件难以直接获取，因此，采用人工建模的方法进行构造。自然风应用相关研究领域包括风力发电、自然通风、城市大气环境评价、污染物排放扩散预测等^[3-7]；国内外学者对所采用的风速条件建模方法已进行了大量的研究。如Sahin等^[8-10]采用一阶马尔科夫链理论，通过逐时风速序列分析，对自然风风速序列进行了建模，结果表明尽管一阶马尔科夫链仅具有一阶相关特性，但90%的建模序列符合实际自然风的统计特性，从而证明了基于马尔科夫链理论风速构造的有效性。Dobigeon等^[11]考虑了风向与风速的联合分布，对风速及风向进行自回归建模，但其采用的样本之间的时间间隔较大，而风向及风速在所研究的时间跨度内相对稳定，因此，构造的风速风向条件为准静态模型。芮晓明等^[12]在风电领域对自然风风速变化模型进行展开研究，为风力发电能力预测提供指导。Cheng等^[1]采用CFD方法生成了动态风速条件，并对该风速条件下的通风效果进行研究，该方法构造的风速条件反映了自然风湍流特性，然而，对于自然风的统计特性未能充分反映。季亮等^[13]应用马尔科夫链对动态自然风风向条件进行了建模，然而并未对相应的动态风速条件进行建模。整体上，国内外对于自然风风速条件的建模基本上针对小时间隔或是更大时间尺度间隔的动态风速条件，并且未能全面考虑自然风的风速统计特性及时序特性，因此，直接用于评价自然通风存在一定缺陷。鉴于通常自然通风每小时换气次数为几次至十几次，本文作者选用分钟作为时间间隔，提出基于马尔科夫链模型等理论的动态风速条件建模方法。该方法考虑了自然风风速统计特性及时序性。进一步对该方法的合理性进行了阐述，并结合实测数据对该方法进行实际应用及有效性验证。

1  理论模型

对于风速分析采用风速的统计特性及时序特性相结合的分析方法，风速统计分析采用最为广泛应用的双参数Weibull统计模型^[16]，风速的时序性分析则采用马尔科夫链结合极大似然理论进行分析。

1.1  双参数Weibull统计模型

目前广泛应用的自然风风速统计模型为双参数Weibull模型，其概率分布函数如下：

          (1)

其中：k为形状因子；c为尺寸因子；F(v)为概率分布函数。

根据式(1)可得：

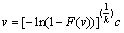        (2)

            (3)

其中：为伽玛函数。在通常情况下，，因此，。

1.2  马尔科夫链模型

马尔科夫链在随机理论文献[15]中有详细阐述。本文仅对马尔科夫链的基本原理进行简述。

马尔科夫链的基本特征为：在给定当前信息的条件下，将来的信息仅取决于当前的信息条件，而与过去的信息条件无关。马尔科夫链是随机变量X₁，X₂，X₃，…的一个序列。序列中变量的取值范围即所有可能的取值的集合定义为“状态空间”。根据马尔科夫链原理，X_n+1仅与X_n相关，即

         (4)

其中：P(·)为概率函数；X_i为时间序列的第i个随机变量；x_i为X_i对应的状态值。

式(4)表明：当X_n取状态值x_n时，X_n+1的取值概率为确定状态。

1.3  极大似然理论模型

极大似然理论模型表述为，对于随机变量X，统计概率模型形式确定，但模型参数不确定，通过若干次试验推断参数值。

极大似然理论表明，已知模型参数能使得某事件发生的概率最大，则随机变量取该事件发生对应的样本值，具体如下。

随机变量X取值空间为{x₁，x₂，x₃，…，x_n}，并且X统计分布模型形式确定，则在一次试验中认为X取值为x_i，其中x_i满足如下概率条件：

 (5)

2  动态风速条件建模

本文构造的动态风速条件主要应用于建筑自然通风的分析及评价。换气次数为自然通风重要的评价指标，而实际建筑自然通风通风次数可达到每小时几次至几十次，因此，考虑到既能反映实际自然风的动态特性能反映自然风的动态特性对自然通风效果的影响。选取分钟为风速的时间间隔，鉴于国内城市典型气象年数据已给出逐时风速风向条件，选取1 h为自然风条件的构造时间总长度。动态风速数据建模流程如图1所示。

图1  动态风速序列构造流程

Fig. 1  Flow chart of dynamic wind speed modeling

在图1的“实测样本数据分析及逐时风速数据获取”部分，基于实测样本数据分析建立目标参数与逐时平均风速回归模型。其中逐时平均风速指当地气象台站或典型气象年的逐时风速，该数据用于构造动态风速序列，目标参数指Weibull统计模型参数(下同)。

2.1  统计风速序列构造

根据国内城市典型气象年数据，逐时平均风速基本低于7.0 m/s，根据实测数据建立Weibull统计模型参数与逐时平均风速之间的回归模型。通过平均风速值可得到相应的Weibull统计模型参数，进而确定风速的统计分布。通过式(2)生成风速序列 (为了便于区分以下称为统计风速序列)，过程见图1中风速序列数值构造部分。

图1中目标参数可基于实测数据求取，根据Weibull分布特性，参数c只取决于风速序列的平均值，因此，确定的平均风速条件下参数c为定值；而对于参数k除了与风速序列的平均值相关外，还与风速的脉动特性相关，因此，相同的平均风速条件下可能对应着多个参数值。为了便于风速构造，平均风速应与参数c及k一一对应，因此，需要对相同平均风速下样本的参数k进行平均化处理(通过上海地区风速数据拟合分析，相同逐时平均风速下，k基本处于平均值±1.0以内，差异较小)，如式(6)所示。

                  (6)

其中：k_i对应的小时风速序列平均值满足。

根据统计学概率分布函数的特性F(v)≤1，首先通过计算生成[0,1]之间的随机数，并将该随机数赋予F(v)。进一步根据目标参数(参数k及c由参数与平均风速回归模型确定)，通过式(2)生成逐分风速序列，由于风速序列数有限，因此，生成风速序列平均值可能与目标值存在较大差异需要进行修正，如式(7)所示。

                 (7)

其中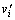：为修正后i时刻风速，m/s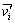；为目标平均风速，m/s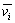；为修正前平均风速，m/s；v_i为修正前i时刻风速，m/s。

2.2  统计风速序列排序

通过风速序列构造流程生成的风速条件满足风速的统计特性，而对于风速的时序特性的反映则基于马尔科夫链及极大似然理论对风速序列数排序。首先根据实测风速数据，按照等数值间距对风速进行数值分段，然后对每个风速分段进行状态赋值，基于马尔科夫链理论确定风速的转移概率矩阵，进一步结合极大似然理论对统计风速序列进行排序。具体排序流程如图1中风速序列数值排序部分。

根据国内城市典型气象年数据，大多情况下逐时平均风速不高于7.0 m/s，因此，以7.0 m/s为逐时平均风速上限，按照0.5 m/s风速间隔进行分段并赋状态值，如表1所示。

基于风速范围赋值定义“转移概率矩阵”：该矩阵中的元素a_i,j表示当前时刻取值为x_i、下一时刻取值x_j的概率，采用P_i,j表示，定义如下：

         (8)

可得转移概率矩阵为

    (9)

表1  风速分段及状态赋值

Table 1  Status value of wind speed

对于矩阵P，可通过分析历史的实测样本数据求得。对于构造的统计风速序列数进行随机排列，则相邻风速之间存在转移概率，如前一时刻风速状态为i，下一时刻风速状态为j，则转移概率为P_i,j，定义变量F为

         (10)

由于风速为一阶马尔科夫链，因此，式(10)中。对于每个风速序列对应唯一的F。根据马尔科夫链特性，F表征了风速确定条件下该风速序列出现的概率。为了保证计算的有效进行，在不影响比较结果的前提下，对矩阵中0元素(表示几乎不会发生，如前一时刻风速为0 m/s后一时刻为10 m/s几乎不会发生)用足够小的数值代替(本文取0.000 1)。根据极大似然理论，风速序列应选取发生概率最高的序列，即变量F最大值对应的风速序列。

统计风速序列为以分钟为间隔以小时为时间长度的风速序列，统计风速序列共计60个风速，直接排序则共计60！种排列方式，对应60！个F。对于该数量级的数据计算已超过常规计算机处理能力，因此，需要首先对风速序列进行平均化处理。根据风工程学理论，自然风10 min平均风速变化较为平稳(风速时程通常取为10 min)^[16]，自然通风动态风速条件建模应保证风速序列的平稳性，因此，采用10 min作为平均化尺度，在10 min内统计风速序列不变，而对10 min平均风速进行排序；相应的转移概率矩阵及基于实测数据10 min间隔平均化后风速通过统计计算获取。风速序列总长度为60 min，则平均化后风速为6个，对应的转移概率定义为

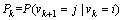(k=1，2，…，5)    (11)

其中：v_k为第k个10 min风速平均值，m/s；如0~10 min风速平均值则为v₁，10~20 min风速平均值则为v₂，依此类推。

可见采用平均化方法后风速的排列方式为6!=720种。对各种排列方式对应的F进行求解，由于10 min内风速序列不变因此进行F比较时按照10 min平均风速转移概率矩阵乘积进行，为了便于比较，对F取对数并不会改变比较过程中的相对大小，定义对数变量F′为

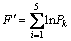               (12)

其中：转移概率矩阵亦基于实测风速10 min平均化平均风速求取，相应状态值如表1所示。F′最大值可能对应多个风速序列，此时通过随机方法抽取目标风速序列，该风速序列即为最终动态风速序列。

根据以上分析风速序列建模过程归纳如下：

(1) 通过实测数据分析建立统计模型参数与逐时平均风速回归模型及马尔科夫链转移矩阵。

(2) 基于逐时风速数据及回归模型生成统计风速序列。

(3) 统计风速序列按照10 min进行平均化处理。

(4) 基于马尔科夫链转移概率矩阵及极大似然模型对平均化风速时间分段进行排序(10 min内风速序列按照统计序列不变)。

(5) 输出步骤(4)排序后的风速序列即为最终动态风速序列。

2.3  建模方法合理性分析

根据风速特性，建模方法合理行分析应包括：构造风速统计特性分析，即构造的风速应能反映实际自然风的统计特性；构造风速的时序性分析，即风速应能反映风速的趋势性。

对于风速统计特性分析，由于风速根据式(2)生成，而式(2)为双参数Weibull分布模型的变形方程，因此，生成风速符合Weibull分布。并且根据平均值及拟合参数目标值对统计风速序列进行修正，进一步保证了构造风速的统计特性与实际自然风的一致性。目标参数c及参数k通过大量实测样本拟合获得，因此，能够反映实际自然风的统计特性。

对于风速时序性，首先基于大量风速实测逐分风速样本进行10 min平均化处理并进行统计建立转移概率矩阵，概率矩阵中元素能够反映实际自然风风速变化特性。进一步对统计风速序列根据平均化风速进行排序，根据转移概率矩阵及极大似然理论对各序列出现概率进行比较并选取出现概率最大的风速序列，因此，构造风速出现的概率最大，表明实际环境中最有可能发生。

通过以上分析可见，动态风速条件建模基于实测数据的统计特性及时序性分析，建模方法合理。

3  模型应用分析

实际应用中多数情况仅有逐时数据(如典型气象年数据)，在求取回归模型及转移概率矩阵基础上可通过本文方法进行逐分风速反演。为了对构造方法的有效性进行对比验证，本文采用某天实测风速。首先基于大量实测样本数据风速建模，再进行验证。测点位于某建筑顶部，周边300 m内建筑均低于该建筑，因此，任何风向条件下测点均处于建筑风影区外。采样仪器为英国GILL公司超声波风速风向仪，型号为WindSonic2，采样方式为连续计测，记录时间间隔为1 min。风速连续测试时间段为2010-11-10—2011-04-10，逐分风速样本量约为200 000个，采用该时间段内样本进行统计模型及转移概率矩阵求取。随机抽取其中某天风速对该方法有效性进行验证，对该天采样风速进行逐时平均，如图2所示，并根据逐时平均风速进行全天逐分风速序列构造。

基于理论模型分析，根据采样期间各小时样本风速Weibull拟合结果(拟合优度均在95%以上，选取其中的1个统计模型拟合结果，如图3所示)，确定统计模型参数与逐时平均风速回归模型如图4所示(参数k已按照式(6)进行了平均化处理)。

图2  随机抽取日逐时风速

Fig. 2  Randomly chosen hour-average wind speed

由图3及图4可见：实测风速样本符合双参数Weibull分布。对于统计模型目标参数c，与逐时平均风速回归结果，呈正比关系并且与理论分析结果 (理论模型部分)相吻合。统计模型目标参数k(平均化后，下同)与逐时平均风速回归结果，呈对数关系。在较小的逐时平均风速条件下，参数k随逐时平均风速的增加，变化速率较快；而在较大的逐时平均风速条件下，参数k随逐时平均风速的增加变化趋于平缓。

图3  实测风速统计模型拟合结果

Fig. 3  Statistic model fitting result of measured wind speeds

图4  统计模型参数与逐时平均风速回归

Fig. 4  Regression of statistic model parameter and hour-average wind speed

将2010-11-10—2011-04-10实测风速按照10 min时间间隔对样本数据进行平均化处理，并按照表1中风速分段对平均化后风速进行状态赋值，进一步统计计算转移概率矩阵，并进行0修正，结果如图5所示。由图5可见：矩阵对角线附近元素数值较大，与对角线距离较远的元素数值较小，这表明数值相近的风速转移概率较高(表现为相应矩阵元素值较大)，而数值相差较大的风速转移概率较低(表现为相应的元素值较小)，如状态为1变化至状态2的概率为0.394，而变化至状态10的概率基本为0，可见实际风速变化较为平稳。

反演风速序列与实测风速对比如图6所示。风速建模基于逐时平均风速，因此，需要进行全天风速序列的整体特性分析。由图6可见：反演风速序列与实测风速序列趋势性相似，整体序列均值、变化幅值及方差较为接近。其中反演风速序列均值为3.01 m/s，实测风速序列均值为2.96 m/s；反演风速序列变化幅值为7.10 m/s，实测风速序列变化幅值为7.00 m/s；反演风速序列标准差为1.35 m/s，实测风速序列标准差为1.37 m/s。全天风速序列数分段频数统计结果及Weibull模型拟合参数(全天数据拟合)对比如图7及表2所示。

由图7及表2可见：反演风速序列的分段频数分布与实测风速分段频数统计结果相吻合，且全天统计模型参数拟合结果十分接近。采用该方法对动态风速进行建模，风速序列能够真实的反映自然风风速特性，从而证明了该方法的有效性。

图5  实测风速变化转移概率矩阵

Fig. 5  Transition matrix of wind speed variation in urban area of Shanghai

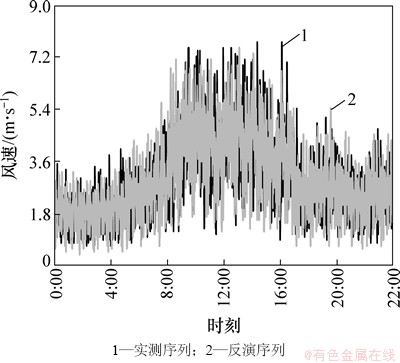
图6  反演风速序列与实测风速序列对比

Fig. 6  Comparison of inversion series data and measure series data

图7  反演数据与实测数值分段频数统计对比

Fig. 7  Comparisons of frequency distribution of inversion data and measured data

表2  反演风速与实测风速拟合结果对比

Table 2  Fitting result comparison of inversion wind speeds and measured wind speeds

4  结论

(1) 基于马尔科夫链及极大似然模型理论提出了自然通风动态风速条件建模方法。与常规方法相比，该方法考虑的时间间隔更小；对于风速特性的反映更为全面，同时考虑了自然风的统计特性及时序特性，并进一步阐述了方法的合理性。

(2) 基于上海地区实测数据，对该方法进行了应用分析。构造了上海地区统计参数与逐时平均风速的回归模型及概率转移矩阵。尺寸因子c与逐时平均风速呈线性变化关系，而平均化后形状因子k与逐时平均风速呈对数变化关系。

(3) 反演风速序列能够有效地反映实测自然风速特性，其中，全天风速序列形状尺寸因子拟合值实测序列为3.27，反演数据为3.33；形状因子实测序列为2.26，反演数据为2.28，其他参数相对偏差亦小于5%，证明了该方法的有效性，从而为实际建筑自然通风评价提供了动态风速条件构造方法，为相关研究提供参考。

参考文献：

[1] CHENG Huhu, Masaaki O, Ryuichilo Y. CFD modeling of unsteady cross ventilation flows using LES[J]. Wind England Aerodyn, 2008, 10/11(4): 1692-1706.

[2] van Hooff T, Blocken B. Coupled urban wind flow and indoor natural ventilation modelling on a high-resolution grid: A case study for the Amsterdam ArenA stadium[J]. Environmental Modelling & Software, 2010, 25(1): 51-65.

[3] LI Gong, SHI Jing. Application of Bayesian model averaging in modeling long-term wind speed distributions[J]. Renewable Energy, 2010, 35(1): 1192-1202.

[4] 黄小培, 覃峥嵘, 韦革宁. 桂西酸雨的季节分布及风向频率统计特征分析[J]. 气象研究与应用, 2008, 29(4): 10-13.

HUANG Xiaopei, QIN Zhengrong, WEI Gening. Seasonal distribution characteristics of acid rain in the west of Guangxi and statistic characteristics of wind direct[J]. Journal of Meteorological Research and Application, 2008, 29(4): 10-13.

[5] Michalski A, Kermel P D, Haug E. Validation of the computational fluid-structure interaction simulation at real-scale tests of a flexible 29 m umbrella in natural wind flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(4): 400-413.

[6] ZHOU Wei, LOU Chengzhi, LI Zhongshi. Current status of research on optimum sizing of stand-alone hybrid solar-wind power generation systems[J]. Applied Energy, 2010, 87(2): 380-389.

[7] Keyhani A, Ghasemi-Varnamkhasti M, Khanali M. An assessment of wind energy potential as a power generation source in the capital of Iran, Tehran[J]. Energy, 2010, 35(1): 188-201.

[8] Sahin A D, Sen Z. First-order Markov chain approach to wind speed modeling[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(4): 263-269.

[9] Pourmousavi Kani S A, Ardehali M M. Very short-term wind speed prediction: A new artificial neural network: Markov chain model[J]. Energy Conversion and Management, 2011, 52(1): 738-745.

[10] D’Amicoa G, Petronib F, Pratticoc F. First and second order semi: Markov chains for wind speed modeling[J]. Physica A: Statistical Mechanics and its Applications, 2013, 392(5): 1194-1201.

[11] Dobigeon N, Turneret J. Joint segmentation of wind speed and direction using a hierarchical model[J]. Computational Statistics & Data Analysis, 2007, 51(2): 5603-5621.

[12] 芮晓明, 马志勇, 康传明. 小尺度风特性建模与分析[J]. 太阳能学报, 2007, 28(12): 1335-1338.

RUI Xiaoming, MA Zhiyong, KONG Chuanming. Modeling and analysis of wind characteristics with little periods[J]. Acta Energiae Solaris Sinica, 2007, 28(12): 1335-1338.

[13] 季亮, 谭洪卫, 王亮. 基于马尔科夫链的自然风风向建模[J]. 中南大学学报(自然科学版), 2012, 43(8): 3274-3279.

JI Liang, TAN Hongwei, WANG Liang. Wind direction modeling using Markov chain[J]. Journal of Central South University: Science and Technology, 2012, 43(8): 3274-3279.

[14] Saleha H A, Abou El-Azm Aly S. Assessment of different methods used to estimate Weibull distribution parameters for wind speed in Zafarana wind farm, Suez Gulf, Egypt[J]. Energy, 2012, 44(1): 710-719.

[15] 刘次华. 随机过程[M]. 第4版. 武汉: 华中科技大学出版社, 2008: 26-30.

LIU Cihua. Stochastic process[M]. 4th ed. Wuhan: Huazhong University of Science and Technology Press, 2008: 26-30.

[16] 阎启, 谢强, 李杰. 风场长期观测与数据分析[J]. 建筑科学与工程学报, 2009, 26(1): 37-42.

YAN Qi, XIE Qiang, LI Jie. Long term observation and data analysis of wind field[J]. Journal of Architecture and Civil Engineering, 2009, 26(1): 37-42.

(编辑  陈爱华)

收稿日期：2013-08-21；修回日期：2013-11-15

基金项目：高等学校博士学科点基金资助项目(20090072110016)

通信作者：谭洪卫(1959-)，男，广西桂林人，博士，教授，从事建筑节能研究；电话：13636582291；E-mail：wangliang0208@163.com