Theoretical and experimental study of initial cracking mechanism of an expansive soil due to moisture-change
来源期刊:中南大学学报(英文版)2012年第5期
论文作者:吴珺华 袁俊平 吴宏伟
文章页码:1437 - 1446
Key words:expansive soil; swell-shrinking deformation; moisture-change; crack; resistivity
Abstract: Swelling and shrinkage due to moisture-change is one of the characteristics of the expansive soil, which is similar to the behavior of most materials under thermal effect. If the deformation is restricted, stress in expansive soil is caused by the swell-shrinking. The stress is defined as “moisture-change stress” and is adopted to analyze swell-shrinkage deformation based on the elasticity mechanics theory. The state when the total stress becomes equal to the soil tensile strength is considered as the cracking criterion as moisture-change increases. Then, the initial cracking mechanism due to evaporation is revealed as follows: Different rates of moisture loss at different depths result in greater shrinkage deformation on the surface while there is smaller shrinkage deformation at the underlayer in expansive soil; cracks will grow when the nonuniform shrinkage deformation increases to a certain degree. A theoretical model is established, which may be used to calculate the stress caused by moisture-change. The depth of initial cracks growing is predicted by the proposed model in expansive soil. A series of laboratory tests are carried out by exposing expansive soil samples with different moisture-changes. The process of crack propagation is investigated by resistivity method. The test results show good consistency with the predicted results by the proposed theoretical model.
J. Cent. South Univ. (2012) 19: 1437-1446
DOI: 10.1007/s11771-012-1160-9![]()
WU Jun-hua(吴珺华)1,2,3, YUAN Jun-ping(袁俊平)1,2, Charles W. W. Ng(吴宏伟)1,2,4
1. Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering,Hohai University, Nanjing 210098, China;
2. Geotechnical Research Institute, Hohai University, Nanjing 210098, China;
3. College of Civil Engineering and Architecture, Nanchang Hangkong University, Nanchang 330063, China;
4. Department of Civil Engineering, Hong Kong University of Science and Technology, Kowloon, Hong Kong, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: Swelling and shrinkage due to moisture-change is one of the characteristics of the expansive soil, which is similar to the behavior of most materials under thermal effect. If the deformation is restricted, stress in expansive soil is caused by the swell-shrinking. The stress is defined as “moisture-change stress” and is adopted to analyze swell-shrinkage deformation based on the elasticity mechanics theory. The state when the total stress becomes equal to the soil tensile strength is considered as the cracking criterion as moisture-change increases. Then, the initial cracking mechanism due to evaporation is revealed as follows: Different rates of moisture loss at different depths result in greater shrinkage deformation on the surface while there is smaller shrinkage deformation at the underlayer in expansive soil; cracks will grow when the nonuniform shrinkage deformation increases to a certain degree. A theoretical model is established, which may be used to calculate the stress caused by moisture-change. The depth of initial cracks growing is predicted by the proposed model in expansive soil. A series of laboratory tests are carried out by exposing expansive soil samples with different moisture-changes. The process of crack propagation is investigated by resistivity method. The test results show good consistency with the predicted results by the proposed theoretical model.
Key words: expansive soil; swell-shrinking deformation; moisture-change; crack; resistivity
1 Introduction
Expansive soil slope failure is one of the most complicated problems in the world [1]. Many analyses have been carried out based on traditional saturated and unsaturated soil mechanics theories, while great differences are still found between the predicted results and measured data in many cases. The reason is that the influence of cracks is not considered during the process of these analyses [2-4]. A good understanding and an operable predictive method for crack propagation would be conducive for slope design and construction.
Cracking problems had been noticed on soil caused by dry-wet cycles in pedology and agricultural field [5]. These are a cause of concern in geotechnical engineering [6-8]. The cracks existing in soil speed up the process of moisture loss, change the soil structure, reduce the soil strength etc. Many tests were carried out to reveal the mechanism and the rules of crack propagation. AYAD et al [9] carried out a field test in order to observe and document the formation of shrinkage cracks in undisturbed weathered sensitive marine clay. In intact clay, the cracks could be found with a spacing of 20-24 cm; while in weathered clay, the average spacing of cracks was 10-12 cm. Moreover, further evaporation resulted in the formation of new vertical cracks in the soil below the sub-horizontal shear plane. KONRAD and AYAD [10-11] presented an idealized framework for the prediction of the spacing between primary shrinkage cracks in cohesive soils undergoing desiccation. The proposed framework was based on the theory of linear elastic fracture mechanics. The principle of effective stresses is used to describe stress partitioning in soils, and a fictitious stress superposition concept was used to predict the average spacing between primary cracks. Then, crack propagation was analyzed with a trapezoidal distribution of total horizontal tensile stress derived from the material constitutive equations. RODRIGUEZ et al [12] showed an analysis of the desiccation process in mining materials based on physical laws. Laboratory tests were performed and a numerical simulation of the measured variables was also carried out. The results showed the formulation using coupled hydromechanical equations took into account the fundamental mechanisms involved in the desiccation process. CHEN et al [13] analyzed the effect of vertical load difference on cracking behaviors by testing and measuring the displacements at the testing points of a large sized real masonry U-shaped model.
The mechanisms of crack propagation revealed in many researches based on the unsaturated soil mechanics theory have been reported in the literature as follows: moisture loss results in suction increasing, tensile state appears when the tensile stress becomes greater than the soil tensile strength and the cracks are caused thereupon. Even though the cracking mechanism in expansive soil seems to be theoretically clear, there are a few deficiencies by using unsaturated soil mechanics theory. Firstly, it takes a long time to obtain the suction equilibrium; secondly, the distribution of suction in soil is still difficult to obtain; thirdly, it is known from a soil water characteristic curve (SWCC) that the matric suction is different at absorption and desorption paths, even if the soil holds the same water content.
It is well-known that water content has significant effects on soil behavior and property [14]. It is reasonable to assume that the swell-shrinkage behavior due to moisture-change is similar to the temperature effect on most solid materials which can be analyzed widely and maturely by thermo-mechanics theory (e.g., water swelling corresponds to expansion with heat; shrinkage corresponds to contraction with cold). Shrinkage test results show that two straight lines with different slopes could describe the relationship between water content and linear-shrinkage ratio [15-16]. The water content at the intersection point of two straight lines is defined as shrinkage limit (Fig. 1). The soil is saturated initially and the water content of soil is usually greater than the shrinkage limit. The relationship between linear-shrinkage ratio and moisture-change for soil is similar to the relationship between linear thermal deformation and the difference in temperature for most solid materials. So, the method for thermal stress and deformation analysis is adopted to analyze the stress due to moisture-change in expansive soil based on elastic mechanics theory.
2 Theoretical considerations
2.1 Moisture-change and swell-shrinkage coefficient
Moisture-change is defined as the difference of the soil water content at a certain time, Wt, with the initial water content W0, and it can be written as ΔW=Wt-W0 (positive during the wetting process), where ΔW is moisture-change. The spatial function of ΔW can be
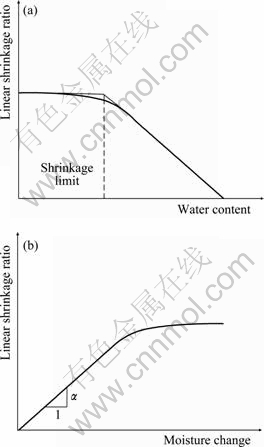
Fig. 1 Shrinkage curve
written as ΔW(x, y, z). Swell-shrinkage coefficient αi of soil is defined as the strain increment resulted from unit moisture-change. It reflects the swell-shrinkage degree of soil due to moisture-change and can be obtained by shrinkage tests mentioned in the introduction. The strain, which is defined as “moisture-change strain” here, will occur due to moisture-change if all boundaries are not fixed. It can be symbolized as αiΔW (i=x, y, z) (positive when expanding). αi is the function of ΔW as αi(ΔW). In this work, only αi under the condition of moisture loss is considered because the cracks are caused due to moisture loss. Moreover, it is known that soil will crack when the water content is less than the shrinkage limit of the soil. Thus, the slope of the idealized shrinkage curve shown in Fig. 1 may be used to define αi. In isotropic soil, αi can be simplified as α because it has no effect on shear strain. So, the strain components due to moisture-change can be expressed as
![]() (i, j=x, y, z) (1)
(i, j=x, y, z) (1)
where δij is Kronecker delta.
2.2 Governing equations
When the soil water content changes continuously, stress is induced because of the internal and external restraints. This stress can be defined as moisture-change stress σmc, which is simplified as σ in this work for convenience wherever appropriate. The total strain contains two parts: one part is caused by moisture-change; the other part is caused by stress based on Hooke’s law. So, the total strain components are
![]() (2)
(2)
where ![]() is Lame’s coefficient;
is Lame’s coefficient; ![]() is shear modulus; μ is Poisson ratio; θ=εxx+εyy+εzz, is volumetric strain; E is deformation modulus.
is shear modulus; μ is Poisson ratio; θ=εxx+εyy+εzz, is volumetric strain; E is deformation modulus.
Equation (2) is the elastic constitutive equation considering the moisture-change stress. The static equilibrium equations, geometric equations and boundary conditions are
![]() (3)
(3)
![]() (4)
(4)
![]()
![]() ;
; ![]()
![]() (5)
(5)
where fi is a known function of body forces; Su is displacement of boundary surfaces; ![]() is a known function of displacement in Su; Sσ is stress boundary surfaces;
is a known function of displacement in Su; Sσ is stress boundary surfaces; ![]() is a known function of surface force in Sσ; nj is the direction cosine.
is a known function of surface force in Sσ; nj is the direction cosine.
Substituting Eqs. (4) and (2) into Eq. (3) without considering the body forces, the governing equations can be derived by displacement method:
![]() (6)
(6)
Equations (5) and (6) are the boundary conditions and governing equations, respectively. Swell-shrinkage deformation αΔW is used to reflect the effect of moisture-change instead of matric suction. There are several advantages here: firstly, the difficulty in determining the matric suction can be avoided; secondly, α and ΔW can be confirmed by routine soil tests. So, the moisture-change stress can be obtained via Eqs. (5) and (6). Moreover, the solution resulted from the loads such as body forces and surface forces can also be absolutely superposed with the solution of moisture-change.
3 Theoretical solutions
In order to solve the moisture-change stress, the displacement potential function is adopted during the process of solving Eq. (6). Because Eq. (6) is an inhomogeneous equation, two steps should be carried out in sequence: 1) One special solution resulted from ΔW should be obtained firstly; 2) One general solution without regard to ΔW should be obtained secondly. Finally, the special and general solutions are superposed and meanwhile, should be satisfied with the boundary conditions.
3.1 Special solution
The displacement potential function, ψ, is introduced and regarded to obtain one special solution:
![]() (7)
(7)
where ![]() is the displacement components corresponding to the special solution.
is the displacement components corresponding to the special solution.
Substituting Eq. (7) into Eq. (6) and it can be rewritten as
![]() (8)
(8)
where ![]() is Hamilton operator.
is Hamilton operator.
If ψ is regarded as Eq.(9) below, Eq.(6) is satisfied obviously and Eq.(7) could be as one special solution:
![]() (9)
(9)
Substituting Eqs. (7) and (9) into Eq. (2), the stress components corresponding to the special solution of displacement should be obtained as
![]() (10)
(10)
where σij is the stress corresponding to the special solution.
3.2 General solution
The general solution should be satisfied in the form of Eq. (6) excluding ΔW:
![]() (11)
(11)
where u″ is the displacement corresponding to the general solution.
The stress components corresponding to the general solution could be obtained via Eq. (2):
![]() (12)
(12)
where σij is the stress corresponding to the general solution.
Moreover, the total displacement components ![]() should satisfy the displacement boundary conditions; the total stress components
should satisfy the displacement boundary conditions; the total stress components ![]() should satisfy the stress boundary conditions. All the equations are derived based on tensor form, so it is directly suitable for plane strain problems. If Eqs. (5), (6), (10) and (12) are rewritten under two dimensional form and E, μ, α are replaced by E(1+2μ)/(1+μ)2, μ/(1+μ) and α(1+μ)/(1+2μ), respectively, the solution of plane stress problems will also be obtained directly.
should satisfy the stress boundary conditions. All the equations are derived based on tensor form, so it is directly suitable for plane strain problems. If Eqs. (5), (6), (10) and (12) are rewritten under two dimensional form and E, μ, α are replaced by E(1+2μ)/(1+μ)2, μ/(1+μ) and α(1+μ)/(1+2μ), respectively, the solution of plane stress problems will also be obtained directly.
The special solution could be obtained exactly via Eq. (10). Sometimes, the general solution could be obtained by Airy stress function in the case of some special boundary conditions.
3.3 Distribution of moisture-change
It can be seen from Eq. (9) that ΔW is an unknown variable which is related to the spatial distribution. Therefore, the distribution of moisture-change should be obtained first of all. Tests on getting soil water content at different depths are carried out. The apparatus is made of transparent plastic and its dimension in detail is shown in Fig. 2. The initial water content of soil is 23.7%. The soil water content at different depths is obtained by drilling holes. The time for sampling is after the 1st, 3rd, 5th and 7th days, respectively, from the beginning of test. The results are given in Table 1. It can be seen that the moisture-change has a positive correlation with depth by and large (note that the moisture-change here is negative). The soil close to the surface evaporates strongly while it is weak deep down. So, the rate of moisture loss close to the surface is greater than that in the deep soil.
It is assumed that the water content only changes along with depth direction for simplicity. In order to obtain the quantitative relationship between moisture- change and depth, according to the test results, the expression of Eq. (13) can be fitted to the measured data. It is revealed that the diffusion rate of water is mainly related to the permeability and drainage conditions of soil. The relation curve between moisture-change and depth is defined as the moisture-change curve:
![]() (13)
(13)
where ΔWmax is defined as the maximum moisture- change (negative when moisture loss); z is depth (m); n is defined as distribution coefficient of moisture- change.
Based on the data in Table 1, the fitted results are given in Table 2. It can be seen that there is little difference in n among these four fitted values. The mean value of n is almost 0.5. ΔWmax decreases as time goes on.
3.4 Moisture-change stress
Based on the above principle, an isotropic model (Fig. 3) which is 2b (b is the half of symmetric parametric length of the model) long and h deep is established under the condition of plane stress. The vertical deformation of the model at the bottom is restrained while the others are free. In addition, it is assumed that 2b>>h and there is no crack initially.
It is known that the method of Airy stress function cannot be applied to solving the problems under the condition with the displacement boundaries. So, it could not be applied directly here. Note that the vertical deformation is restrained at z=0 while the others are free. This means that z-axis is a symmetric axis here. So, the analysis model could be transformed into the calculation model shown in Fig. 4. The z-displacement at z=0 is obviously equal to zero after transformation and meanwhile all the boundaries are free. Therefore, the method of Airy stress function could be applied directly in this model.
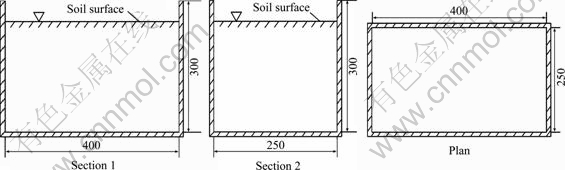
Fig. 2 Schematic diagram of test model (Unit: mm)
Table 1 Water contents in different depths due to evaporation in laboratory
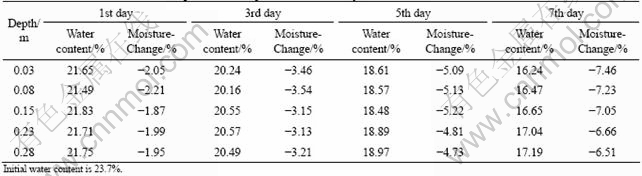
Table 2 Fitted results on moisture-change and depth relationship via Eq. (13
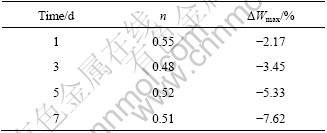

Fig. 3 Analysis model

Fig. 4 Calculation model
In order to adjust to the coordinate system in Fig. 4, the expression of moisture-change curve should be rewritten as ![]() , where h is the effective depth, m. Its maximum is the depth of climate influence as a rule. If the actual depth we adopt is less than the depth of climate influence, h is the actual depth. Otherwise, h is the depth of climate influence. It could be seen that the expression was not convenient for providing a solution because of the non existence of the first derivative at z=0. In order to solve this problem, quadratic function instead of original exponential function is adopted to assure the derivability. So,
, where h is the effective depth, m. Its maximum is the depth of climate influence as a rule. If the actual depth we adopt is less than the depth of climate influence, h is the actual depth. Otherwise, h is the depth of climate influence. It could be seen that the expression was not convenient for providing a solution because of the non existence of the first derivative at z=0. In order to solve this problem, quadratic function instead of original exponential function is adopted to assure the derivability. So, ![]() is obtained as the approximate expression of moisture-change curve hereby, where A=
is obtained as the approximate expression of moisture-change curve hereby, where A=
![]() ,
, ![]() .
.
Substituting the approximate expression of moisture-change curve into Eq. (9) and noted that it is a plane stress problem, it can be written as
![]() (14)
(14)
According to the form of right expression of Eq.(14), ![]() is obtained obviously, where m is an unknown constant. Substituting into Eq. (14), it can be rewritten as m=(1+μ)α and
is obtained obviously, where m is an unknown constant. Substituting into Eq. (14), it can be rewritten as m=(1+μ)α and ![]() . So, the solution will be obtained based on Eq. (10):
. So, the solution will be obtained based on Eq. (10):
![]()
![]() ,
, ![]() (15)
(15)
The result of surface force is shown in Fig. 5. It could be seen that the normal stress is symmetric and the symmetry axes are x-axis and z-axis. The values at the top and bottom of this model are greater than the values in the middle. They are determined by the expression of moisture-change curve. In addition, there is actually no external force on any of the boundaries. Another surface force has to be applied on the left and right sides. This surface force is equal and opposite compared with the initial surface force in order to satisfy the boundary conditions. Then, the stress results could be regarded as the general solution. Because 2b>>h, the surface force can be simplified to a uniform surface force according to the Saint-Venant’s principle. This conversion is beneficial to obtaining the general solution easily. Moreover, the results of stress are still exact in the most area but the boundaries nearby.
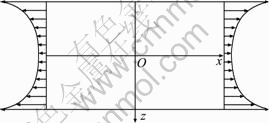
Fig. 5 Surface forces distribution for special solution
The stress function could be written as φ=Cz2 for the uniform surface force based on elastic mechanical theory, obviously, and the following results could be ![]() ,
, ![]() , where C is an unknown constant. Thus, the total stress components are pointed out as
, where C is an unknown constant. Thus, the total stress components are pointed out as
![]() (16)
(16)
The external forces on all boundaries are zero. Based on the Saint-Venant’s principle, the equations of force balance and moment balance should be satisfied in all boundaries. Two equations can be written as
![]() ,
, ![]() (17)
(17)
Then, the constant C can be obtained as
![]() .
.
Thus:
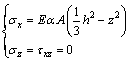 (18)
(18)
Corresponding to the real conditions, Eq. (18) is rewritten as
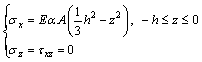 (19)
(19)
Equation (19) is the final expression of moisture-change stress and it satisfies all boundary conditions. It should be pointed out that the calculation results of stress σx via Eq. (19) is an increment as Δσx caused by ΔW actually. In this work, it is assumed that the soil is saturated initially so that the initial moisture- change stress σ0 is equal to zero. The water content measured during testing should be greater than the shrinkage limit. Therefore, the real stress is Δσx.
In addition, Eq. (19) indicates that the moisture- change stress will be equal to zero and the moisture- change curve is changed into a vertical line if n=0. This means that the rate of moisture loss is the same in different positions. Though the soil evaporates continuously, the moisture-change stress is not caused without restraining. Macroscopically, the soil will shrink uniformly without cracking. This reveals an important conclusion on the cracking mechanism of soil due to evaporation as follows: the shrinkage deformation is resulted from moisture loss. The rate of moisture loss of soil at different positions is different. This results in different shrinkage deformations. The rate of moisture loss of soil close to the surface is greater than that of the deep soil, and the shrinkage deformation near the surface is greater than that of the deep soil too. This will lead to the non-uniform shrinkage deformation. The degree of non-uniform shrinkage deformation is related to soil properties and climatic conditions. The cracks will be caused when the non-uniform shrinkage deformation develops to a certain degree. The key factor of cracking obtained from the analysis is not only the moisture loss, but also the different rates of moisture loss at different positions in soil. Matric suction as the judgment criterion on cracking was put forward [17]. It is known that matric suction increases due to moisture loss from soil water characteristic curve (SWCC). However, soil may not crack even though it has high matirc suction due to moisture loss. Moreover, it should satisfy the condition of nonuniform shrinkage. Cracking may not be caused without regard to this key condition, in spite of existing high matirc suction.
4 Analysis of initial cracking
4.1 Initial depth of crack
The results are obtained under the condition without cracking, so it could be the judgment on initial cracking in soil. The cracks are caused by non-uniform shrinkage resulted from moisture loss without external forces. According to the criterion of maximum tensile stress, the soil begins to crack when the moisture-change stress σx is equal to the tensile strength σt, and σx=σt at the bottom of the crack. Substituting this equation into Eq.(19), the following equation can be written:
![]() (20)
(20)
where lc is the initial depth of crack. Substituting the expression of A into Eq. (20), the equation can be rewritten as
![]() (21)
(21)
When lc=0, the initial critical value of moisture-change can be worked out:
![]() (22)
(22)
where ΔWini is defined as initial critical value of moisture-change. This means that the water content can be predicted when the soil will soon crack if the initial water content is obtained. Here, the initial status of soil is saturated, and the initial moisture-change stress is zero thereupon. So, when the moisture-change is close to the initial critical value of moisture-change, cracks will soon be caused. It is known that the soil can be prevented from cracking by decreasing the moisture loss effectively.
4.2 Verification of theoretical model
The soil parameters are listed in Table 3. All the parameters are measured from many researches [18-20]. The effective depth is 2.0 m. The size of model is 8 m in length (horizontal) and 2 m in height (vertical). The deformation at the bottom of the model is restrained in a vertical direction while the others are free. The stress results in the middle of horizontal direction are drawn based on Saint-Venant’s principle. The results obtained by a self-programming using FEM under the same conditions are also shown in Fig. 6 in order to compare with the theoretical results. The results of different calculation methods present good consistency and the results are close to each other. The value of moisture-change stress is positive (tensile stress) primarily and decreases along with the depth increasing. It is equal to tensile strength at a certain depth which is defined as the initial depth of crack. With the increase of depth sequentially, stress is still positive but less than tensile strength. When stress is equal to zero, the position here is in a critical state without compression and tension. After that, the value of moisture-change stress becomes negative (compressive stress) and the soil is under compression in deep soil. The moisture-change stress is greater when the soil weight is considered. It is evident that the validity of this idealized model is verified. It is shown in Fig. 6 that soil weight and tensile strength of soil have effects on the initial depth of crack.
Table 3 Soil parameters

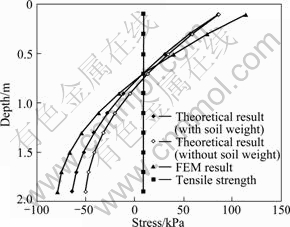
Fig. 6 Results with different methods (x=4 m)
Several advantages of this proposed model are summed up here. Firstly, moisture-change instead of matric suction has been adopted to analyze the mechanical behavior of expansive soil. The difficulty and complexity of measuring matric suction can be avoided. In contrast, moisture-change can be obtained easily in practical engineering. Secondly, the proposed model is conveniently established; it has clearness in principle and reliability in result. All parameters have specific physical meanings and it is convenient for confirming them. Thirdly, the development law of cracking can be predicted and analyzed in some simple boundary conditions. Last, but most importantly, the mechanism of crack formation can be revealed distinctly and essentially. It is beneficial for us to further understand the related properties of expansive soil.
In Fig. 6, it can be seen that the initial depth of crack is about 0.8 m with use of the parameters in Table 3. Actually, the depth of crack observed in practical engineering is from 1.5 to 3 m [21-22] in practical engineering. It is affected by many factors such as geological structure, wetting-drying cycles, variable temperature, and unloading. So, the result calculated with this theoretical model only affected by moisture loss is less than the observed depth of crack in practical engineering. Nevertheless, the initial depth of crack is still applied to designing and analyzing. The influencing laws of different parameters affecting the initial depth of crack can be obtained, and it can be an available reference for designing and constructing to avoid cracking.
5 Testing program and comparisons
5.1 Testing technique
First of all, one method to estimate the water content of surface soil indirectly is introduced and applied in this work by measuring soil resistivity. Resistivity is a physical quantity which could reflect the electrical conductivity of different materials. The definition formula for resistivity is as follows:
F=ρS/L (23)
where F is resistivity, Ω·m; ρ is resistance, Ω; S is sectional area, m2; L is length, m.
The microstructure morphology of soil based on Refs. [23-25], and physical and mechanical properties presented by several authors [26-28] have been studied with the resistivity method. ARCHIE [29], GEORGE et al [30] and WAXMAN and SMITS [31] had put forward several resistivity models on saturated cohesionless soil, unsaturated cohesionless soil and cohesive soil, respectively. The influencing factors of electrical conductivity of soil are listed according to descending influence as follows: water content, liquid resistivity in void, temperature, porosity, etc. In practical engineering, water content changes a lot following the actual conditions, while the other factors only change a little. This means that water content is the main factor which affects soil resistivity, much more than others. So, the relationship between resistivity and water content should be obtained firstly.
The actual depth of crack could be detected with a long, hard filament as the dimensions of testing model are small (i.e., 400 mm×250 mm×300 mm). The schematic diagram of detecting crack depth is shown in Fig. 7. So, the actual depth of crack and the surface soil resistivity could be measured at the same time.
5.2 Testing apparatus
The parameters of expansive soil are listed in
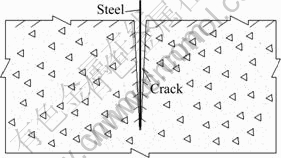
Fig. 7 Schematic diagram of detecting crack depth
Table 4. The parameters are obtained from an expansive soil slope in Xinxiang, Henan Province, China. The apparatus is the same as the one shown in Fig. 2. The difference is that several small stainless steel pins are evenly laid in the surface soil with the same spacing (30 mm) to measure the surface soil resistivity. This model cannot be made large enough to avoid disturbance when sampling during the test. So, the method of measuring the soil resistivity has been adopted to get the water content of soil indirectly.
5.3 Pre-test
For the sake of measuring the water content of surface soil, the resistivity of soil with different dry density and water content are measured initially to get the relationship between them. The specimens of different dry density and water content are made by cutting rings (D=61.8 mm, H=20 mm). Two small stainless steel pins are laid in each specimen to measure the soil resistivity (Fig. 8). They are centrosymmetric and the space is 30 mm along the diametrical direction.
Figure 9 shows the results of the relationship between the dry density, water content and the soil resistivity. It can be seen that the soil resistivity has a negative correlation with the water content and dry density. The more water content the soil contains, the better the conductivity. The greater the dry density, the tighter the particles contact with each other. This will increase the electric conductive area to enhance the conductivity. So, the resistivity gets smaller consequently. A formula could be fitted with the data in Fig. 9 as follows:
![]() (24)
(24)
where w is water content, %; ρd is dry density, kg/m3; a, b, c are the unknown coefficients.
Adopted by multiple linear regressions, these coefficients are obtained as follows: a=-4.77, b=0.088, c=2.76×10-3. Equation (24) could be transformed into Eq. (25) as follows:
![]() (25)
(25)
where F′=1/F. This means if the dry density and resistivity are known already, the water content could be gotten via Eq. (25). Therefore, this formula could be applied to obtaining the water content of surface soil.
5.4 Testing scheme
Because it is easier to make specimens in the laboratory, a series of laboratory tests focused on the different maximum moisture-changes have been carried out to obtain essential data. The scheme of different maximum moisture-changes is explained as follows: the water content could be obtained by measuring the resistivity of surface soil via Eq. (25). The maximum moisture-change could be achieved if the initial soil water content is known. So, laboratory tests have been carried out according to the scheme. The initial water content of surface soil is 23.63% and dry density is 1 710 kg/m3. The temperature and humidity in the laboratory are 20 °C and 75%, respectively. The surface soil resistivity is measured every half an hour from the beginning of the test. The resistivity between two pins with the same space is measured. Then, all the results are averaged as a mean value of surface soil at present. It should be noticed that, as far as possible, there must be no cracks between two pins which are applied to measuring the soil resistivity exactly.
Table 4 Parameters of expansive soil in Xinxiang city, Henan Province, China

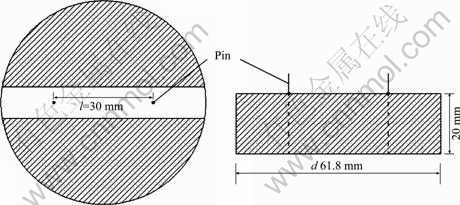
Fig. 8 Specimen’s shape and position of pins for measuring resistivity
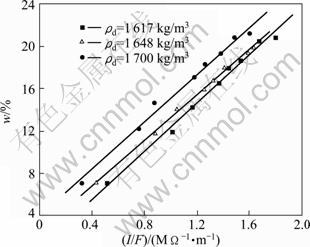
Fig. 9 Dry density, water content and resistivity relationship
5.5 Comparison with test results
After about 14 h, the visible primary cracks are produced. The calculated parameters measured by tests are listed in Table 3. Here, the effective depth is 0.3 m, which is the height of specimen. Meanwhile, the depth of crack which is defined as calculated depth via Eq. (21) is obtained. The water content of surface soil could be obtained indirectly with Eq. (25) by measuring the resistivity of surface soil, and the maximum moisture-change could also be obtained at the same time. Then, the actual depth of crack, defined as the measured depth, is measured by a long, hard filament mentioned above. The results are shown in Table 5.
Table 5 Results on scheme of different maximum moisture- changes
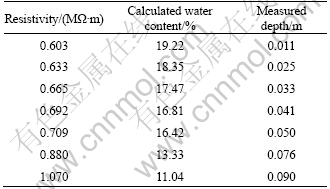
At present, the mean resistivity value of surface soil is 0.588 MΩ·m and the water content calculated with Eq. (25) is 19.74%. Based on the parameters in Table 3 via Eq. (22), ΔWini is -4.04% while the actual ΔW is -3.89%. The two methods give very similar results. So, Eq. (22) can be used to predict the characteristics of initial cracking.
The results between the calculated depth and the measured depth are shown in Fig. 10. The measured depth is greater than the calculated depth along with the increase of moisture-change. It could be explained as follows: when the surface soil would be about to crack, evaporation surfaces include not only the original surfaces but also the new crack surfaces. This will certainly make the rate of water loss accelerated, and the depth of crack larger than the calculated result. Nonetheless, it could be seen that the measured and calculated results of the depth of crack are, generally, consistent with each other. These two results are obtained without any large difference. Therefore, the rationality of the theoretical model is further verified.
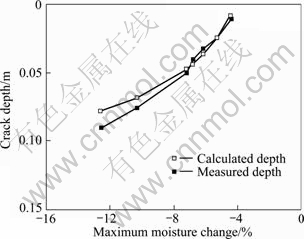
Fig. 10 Results of calculated and measured crack-depth
6 Conclusions
1) A method of using moisture-change instead of matric suction is presented to analyze the swell- shrinkage deformation caused by moisture-change. Moisture-change stress could be adopted to solve the problems of swell-shrinkage deformation caused by moisture-change. A theoretical model adopting moisture-change to calculate moisture-change stress is set up hereby. The cracking mechanism of soil is summed up as follows: the shrinkage deformation is resulted from moisture loss. The rate of moisture loss close to the surface is greater than that the deep soil, and the shrinkage deformation near the surface is greater than that of the deep soil too. This will lead to the non-uniform shrinkage deformation. The cracks will be caused when the nonuniform shrinkage deformation develops to a certain degree. The key factors of cracking the moisture loss but also the different rates of moisture loss in different positions in soil are obtained from the analysis.
2) Many advantages of this proposed model are listed. First, moisture-change instead of matric suction is adopted to analyze mechanical behavior of expansive soil. The difficulty and complexity of measuring matric suction can be avoided. In contrast, moisture-change can be gotten easily in practical engineering. Second, this model is established conveniently; it has clearness in principle. All parameters have specific physical meanings and can be obtained conveniently. Third, the law of initial cracking can be predicted and analyzed in some simple boundary conditions. Last but most importantly, the mechanism of crack formation can be revealed distinctly and essentially.
3) The expressions of initial depth of crack and critical initial moisture-change in expansive soil due to evaporation are deduced. A series of laboratory tests are carried out according to the scheme in different maximum moisture-changes. The method of measuring soil resistivity to obtain the water content of surface soil indirectly has been adopted and it is proved. The correctness of the proposed model is verified by the experimental results.
4) It should be mentioned that the analytical solution is based on Saint-Venant’s principle. Hence, inevitably, there are still some limitations. How to ameliorate this proposed model should be researched in future.
References
[1] LI Sheng-lin. Studies on the engineering geology of expansive soil in China [M]. Nanjing: Jiangsu Science and Technology Publishing House, 1992: 2-16. (in Chinese)
[2] MORRIS P H, GRAHAM J, WILLIAMS D J. Cracking in drying soil [J]. Canadian Geotechnical Journal, 1992, 29: 263-277.
[3] YAO Hai-lin, ZHENG Shao-he, CHEN Shou-yi. Analysis on the slope stability of expansive soil considering cracks and infiltration of rain [J]. Chinese Journal of Geotechnical Engineering, 2001, 23(5): 606-609. (in Chinese)
[4] CHEN Sheng-shui, ZHENG Cheng-feng, WANG Guo-li. Researches on long-term strength deformation characteristics and stability of expansive soil slopes [J]. Chinese Journal of Geotechnical Engineering, 2007, 29(6): 795-799. (in Chinese)
[5] RITCHIE J T. Water movement in unsaturated swelling clay soil [J]. Journal of the Soil Science Society of America, 1972, 36: 874-879.
[6] XIE Hai-feng, RAO Qiu-hua, XIE Qiang, LI Zong-yu, WANG Zhi. Effect of holes on in-plane shear (Mode II) crack sub-critical propagation of rock [J]. Journal of Central South University of Technology, 2008, 15(s1): 453-456.
[7] CHEN Feng, XU Ji-cheng. Computer controlled method for measurement of surface crack length on plate subjected to fatigue loading [J]. Journal of Central South University of Technology, 1997, 4(2): 141-143.
[8] LEE F H, LO K W, LEE S L. Tension crack development in soils [J]. Journal of Geotechnical Engineering, ASCE, 1988, 14(8): 915-929.
[9] AYAD R, KONRAD J M SOULIE M. Desiccation of sensitive clay: Application of the model crack [J]. Canadian Geotechnical Journal, 1997, 34(6): 943-951.
[10] KONRAD J M, AYAD R. An idealized framework for the analysis of cohesive soils undergoing desiccation [J]. Canadian Geotechnical Journal, 1997, 34(4): 477-488.
[11] KONRAD J M, AYAD R. Desiccation of a sensitive clay: Field experimental observations [J]. Canadian Geotechnical Journal, 1997, 34(6): 929-942.
[12] RODRIGUEZ R, SANCHEZ M, LEDESMA A, LLORET A. Experimental and numerical analysis of desiccation of a mining waste [J]. Canadian Geotechnical Journal, 2007, 44(6): 644-658.
[13] CHEN Da-chuan, SHANG, Shou-ping, ZHANG Cheng-qiang. Effect of vertical load difference on cracking behaviors in multistory masonry buildings and numerical simulation [J]. Journal of Central South University of Technology, 2009, 16(6): 1014-1021.
[14] CHARLES W W NG, BRUCE M. Advanced unsaturated soil mechanics and engineering [M]. London: Spon Press, 2007: 279-286.
[15] TAY Y Y, STEWART D I, COUSENS T W. Shrinkage and desiccation cracking in bentonite-sand landfill liners [J]. Engineering Geology, 2001, 60(1): 263-274.
[16] KODIKARA J K, CHOI X. A simplified analytical model for desiccation cracking of clay layers in laboratory tests [C]// Proceedings of the 4th International Conference on Unsaturated Soils. Carefree, Arizona: Geotechnical Special Publication, 2006: 2558-2569.
[17] LI Pei-yong, YANG Qing, LUAN Mao-tian, WANG Dong-lin. Research on influential factors of crack propagation depth of unsaturated expansive soils [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(S1): 2967-2972. (in Chinese)
[18] YESILLER N, MILLER C J. Desiccation and cracking behavior of three compacted landfill liner soil [J]. Engineering Geology, 2000, 57(2): 105-121.
[19] YU Fei, CHEN Shan-xiong, XU Xi-chang, YU Song. Characteristics and mechanism of California bearing ratio of expansive soil [J]. Rock and Soil Mechanics, 2007, 28(6): 1113-1117. (in Chinese)
[20] CHEN Jian-bin, Kong L W, GUO Ai-guo, ZHAO Yan-lin, LU Hai-bo. Deformation characteristics of expansive soil slopes under precipitation and evaporation [J]. China Civil Engineering Journal, 2007, 40(11): 70-77. (in Chinese)
[21] YAO Hai-lin, CHENG Ping, WU Wan-ping. A simplified method for predicting heave in expansive soil grounds based on three dimensional shrinkage tests [J]. Rock and Soil Mechanics, 2004, 25(11): 1688-1692. (in Chinese)
[22] PAN Z J, XIE Y L, YANG X H. Depth identification of the active and cracking zones in expansive soil from in-situ suction measurement [J]. Journal of Engineering Geology, 2006, 14(2): 206-211.
[23] RHOADES J J, MANTEGHI N A, SHOUSE P J. Soil electrical conductivity and soil salinity: new formulations and calibrations [J]. Soil Science Society of American Journal, 1989, 53: 433-439.
[24] ABU-HASSANEIN Z, BENSON C, BLOTZ L. Electrical resistivity of compacted clays [J]. Journal of Geotechnical Engineering, ASCE, 1996, 122(5): 397-406.
[25] CAMPANELLA R G, WEEMEES I. Development and use of an electrical resistivity cone for groundwater contamination studies [J]. Canadian Geotechnical Journal, 1990, 27: 557-567.
[26] LIU Guo-hua, WANG Zhen-yu, HUANG Jian-ping. Research on electrical resistivity feature of soil and its application [J]. Chinese Journal of Geotechnical Engineering, 2004, 26(1): 83-87. (in Chinese)
[27] LIU Song-yu, HAN Li-hua, DU Yan-jun. Experimental study on electrical resistivity of soil-cement [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(11): 1921-1926. (in Chinese)
[28] ARULMOLI K, ARULANANDAN K, SEED H B. New method for evaluating liquefaction potential [J]. Journal of Geotechnical Engineering Division, ASCE, 1985, 111(1): 95-114.
[29] ARCHIE G. The electrical resistivity log as an aid in determining some reservoir characteristics [J]. Transactions of American Institute of Mining Engineers, 1942, 146: 54-62.
[30] GEORGE V, KELLER, FRANK C, FRISCHKNECHT F. Electrical methods in geophysical prospecting [M]. Oxford: Pergamon Press, 1996: 123-133.
[31] WAXMAN M H, SMITS L J M. Electrical conductivity in oil-bearing shale sand [J]. Society of Petroleum Engineers Journal, 1968, 65: 1577-1584.
(Edited by YANG Bing)
Foundation item: Project(2006BAB04A10) supported by the National Science and Technology Pillar Program during the 11th Five Year Plan of China; Project(51008117) supported by the National Natural Science Foundation of China
Received date: 2011-03-14; Accepted date: 2011-07-14
Corresponding author: YUAN Jun-ping, Associate Professor, PhD; Tel: +86-13815861109; E-mail: yuan_junph@hhu.edu.cn

