
DOI: 10.11817/j.issn.1672-7207.2020.12.015
液驱并联机构多维力加载系统滑模解耦控制
赵劲松1, 2, 3,孙鑫宇3,董杰3,王春发3,徐嘉祥3,王志鹏3
(1. 燕山大学 河北省重型机械流体动力传输与控制实验室,河北 秦皇岛,066004;
2. 浙江大学 流体动力与机电系统国家重点实验室,浙江 杭州,310027;
3. 燕山大学 机械工程学院,河北 秦皇岛,066004)
摘要:针对液驱并联机构多维力加载系统频响低、耦合力强、参数时变和模型摄动的问题,提出一种改进的滑模控制策略以提高系统响应速度与输出精度。首先,建立多维力加载系统刚柔混合动力学模型与液压系统模型,推导不同位姿下系统闭环传递函数,分析各通道间耦合力产生机理。其次,考虑多维力加载系统模型实际质量矩阵和刚度矩阵的不确定性,提出名义矩阵补偿方法。基于系统补偿模型,构建滑模控制器名义模型,进而利用力跟踪误差确定控制器二阶滑模面,探索滑模面收敛条件,分析控制参数对力跟踪误差收敛速度的影响。在此基础上,采用线性化反馈技术,确定滑模控制律。最后,根据李雅普诺夫定理分析提出的控制结构稳定性,得到渐进稳定的充分条件。研究结果表明:在工作频段,相较于传统PI控制,滑模控制的多维力加载系统通道间耦合力范围减小86.5%,耦合力矩范围减小66%;广义质量矩阵和广义刚度矩阵的非对角性是多维力加载系统产生耦合力的主要因素,改进的滑模控制器能够克服多维力加载系统的建模误差,提高系统的动态响应速度及对外部扰动的鲁棒性。
关键词:电液伺服;并联机构;多维力加载;力耦合;变结构控制
中图分类号:TH137 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207(2020)12-3407-11
Sliding mode decoupling control for electro-hydraulic multi-dimensional force loading system with parallel mechanism
ZHAO Jinsong1, 2, 3, SUN Xinyu3, DONG Jie3, WANG Chunfa3, XU Jiaxiang3, WANG Zhipeng3
(1. Hebei Provincial Key Laboratory of Heavry Machinery Fluid Power Transmission and Control, Yanshan University, Qinhuangdao 066004, China;
2. State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, Hangzhou 310027, China;
3. School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China)
Abstract: Aiming at the problems of low frequency response, strong coupling force, time-varying parameters and model perturbation in the electro-hydraulic multi-dimensional force loading system with parallel mechanism, an improved sliding mode control strategy was proposed to improve the response speed and output precision of the system. Firstly, the rigid-flexible hybrid dynamic model and hydraulic system model of the multi-dimensional force loading system were established, and the closed-loop transfer function of the system in each posture was derived. Then the coupling force generation mechanism between each channel was analyzed. Secondly, considering the uncertainty of the actual mass matrix and stiffness matrix of the multi-dimensional force loading system model, a nominal matrix compensation method was proposed. Based on the system compensation model, the nominal model of the sliding mode controller was constructed. Then the second-order sliding mode surface of the controller was determined by the force tracking error. Furthermore, the convergence conditions of the sliding mode surface was explored. The influence of the control parameters on the convergence rate of the force tracking error was analyzed. On this basis, the sliding mode control law was determined by linear feedback technology. Finally, according to Lyapunov theorem, the sufficient condition of asymptotic stability was obtained. The results show that in the working frequency band, compared with the traditional PI control, the coupling force range and the coupling torque range among the channels of multi-dimensional force loading system by sliding mode control reduce by 86.5% and 66%, respectively. The non-diagonality of generalized mass matrix and generalized stiffness matrix is the main factor of coupling force in multi-dimensional loading system. The improved sliding mode controller can not only overcome the modeling error of multi-dimensional loading system, but also improve the dynamic response speed of the system and the robustness against the external disturbances.
Key words: electro-hydraulic servo; parallel mechanism; multi-dimensional loading; force coupling; variable structure control
基于Stewart平台的液驱并联机构多维力加载系统(electro-hydraulic multi-dimensional force loading system with parallel mechanism,EH-MDLPM)具有自由度多、结构紧凑、刚度大和承载能力强的优点[1-2],因此,它被广泛应用在机器人、数控机床、医疗器械以及航空航天机械等多个领域[3-4]。EH-MDLPM各通道间存在耦合力干扰,传统控制方法难以满足其动态性能和加载精度要求[5-6],因此,针对上述问题,研究相应的控制方法具有重要意义。
针对飞行模拟器操纵负荷力加载控制系统不稳定现象,王辉等[7]采用前馈补偿和PID反馈调节相结合的复合控制算法提高系统稳定性,但力加载跟踪仍存在约8%的相对误差;王博等[8]采用PID控制及动压反馈控制将正交并联六自由度力控系统加载误差降低到1%,然而,该系统存在严重输出力耦合现象;UKIDVE等[9]假设雅可比矩阵恒定不变,利用此性质设计出具有容错能力的并联机构,提高其运动精度且实现工作范围局部解耦;YANG等[10]利用3个RPRS支腿支撑运动平台,其他支腿关节轴垂直基面且相互平行,实现并联机构工作范围全域解耦,但该机构结构复杂且搭建困难;赵春红等[11]提出二阶滑模控制器,抑制外界波形干扰,提高驱动液压缸活塞运动轨迹的输出精度与控制系统的稳定性;张达等[12]提出自适应滑模控制器,有效估计并克服3-UPS/PU并联机构关节摩擦干扰,消除驱动的抖振现象,提高系统控制精度与动态品质;刘希等[13]提出自适应反演滑模控制器,实现并联运动平台支链电液伺服运动快速、稳定和高精度位置控制,且对系统的外加干扰具有很强的鲁棒性;黄道敏等[14]提出分数阶积分滑模控制器,提高六自由度水下机械手系统收敛的快速性与抗干扰能力。考虑到并联机构的结构固有属性、柔性负载引起的耦合影响和力控系统解耦的复杂性,将滑模控制用于EH-MDLPM中进一步研究。
本研究以降低EH-MDLPM耦合力为目的,建立其模型,分析其耦合机理,并采用改进的滑模控制器提高系统控制性能。基于Lyapunov定理分析该控制方法的稳定性。通过实验,验证改进滑模控制方法在参数时变系统中的有效性,为EH-MDLPM解耦提供了一种有效控制方法。
1 系统建模
图1所示为Stewart平台结构简图。由图1可见:多维力加载系统采用Stewart平台为基础结构,上平台通过胡克铰,活塞杆以及液压缸筒连接下平台。以上平台中心为坐标原点,建立与上平台固连的动坐标系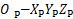 ,当上平台至运动中心位置时,动坐标系重合于惯性坐标系
,当上平台至运动中心位置时,动坐标系重合于惯性坐标系 ,
, 为第
为第 个上铰点在动坐标系中的坐标矢量,
个上铰点在动坐标系中的坐标矢量, 为第
为第 个下铰点在惯性坐标系中的坐标矢量。工作时,活塞杆伸缩,输出力和位移,通过胡克铰将力和位移传递到上平台,实现上平台广义空间六自由度力加载。
个下铰点在惯性坐标系中的坐标矢量。工作时,活塞杆伸缩,输出力和位移,通过胡克铰将力和位移传递到上平台,实现上平台广义空间六自由度力加载。

图1 Stewart平台结构简图
Fig. 1 Stewart platform structure diagram
1.1 动力学建模
EH-MDLPM动力学建模如下[15]。
Stewart平台的运动学反解矩阵方程为
 (1)
(1)
式中: 为6个液压缸的位置矩阵;
为6个液压缸的位置矩阵; 为上平台各铰点在动坐标系下的位置矩阵;
为上平台各铰点在动坐标系下的位置矩阵; 为下平台各铰点在惯性坐标系下的位置矩阵;
为下平台各铰点在惯性坐标系下的位置矩阵;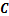 为上平台中心在惯性坐标系下的位置矩阵;
为上平台中心在惯性坐标系下的位置矩阵; 为动坐标系与惯性坐标系之间旋转变换矩阵。
为动坐标系与惯性坐标系之间旋转变换矩阵。
工作空间中EH-MDLPM动力学模型为
 (2)
(2)
式中: 为自由度空间广义质量矩阵;
为自由度空间广义质量矩阵;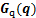 为自由度空间重力项矩阵;
为自由度空间重力项矩阵;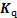 为弹性负载在工作空间的刚度矩阵;
为弹性负载在工作空间的刚度矩阵;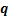 为上平台的广义位移;
为上平台的广义位移; 为上平台的广义加速度;
为上平台的广义加速度; 为广义速度与缸伸缩速度的雅可比矩阵;
为广义速度与缸伸缩速度的雅可比矩阵; 为各支腿输出的力矢量。
为各支腿输出的力矢量。
关节空间中EH-MDLPM动力学方程为
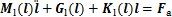 (3)
(3)
式中: 为6个液压缸的加速度矩阵;
为6个液压缸的加速度矩阵;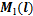 为关节空间广义质量矩阵;
为关节空间广义质量矩阵; 为关节空间重力项矩阵;
为关节空间重力项矩阵;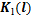 为关节空间刚度矩阵。
为关节空间刚度矩阵。
根据上述建模可建立多维力加载系统并联机构的动力学框图,如图2所示,表示各支腿液压缸输出力克服重力、弹性力及其惯性力从而产生位移。

图2 多维力加载系统并联机构的动力学框图
Fig. 2 Dynamic diagram of parallel mechanism of multi-dimensional loading system
1.2 液压动力元件建模
EH-MDLPM采用非对称液压缸作为执行机构进行力加载,阀控非对称液压缸原理图如图3所示,图3中 为活塞杆无杆腔压力;
为活塞杆无杆腔压力; 为活塞杆无杆腔面积;
为活塞杆无杆腔面积; 为活塞杆无杆腔流量;
为活塞杆无杆腔流量; 为活塞杆有杆腔压力;
为活塞杆有杆腔压力;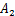 为活塞杆有杆腔面积;
为活塞杆有杆腔面积; 为活塞杆有杆腔流量;
为活塞杆有杆腔流量; 为进油压力;
为进油压力;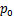 为出油压力。
为出油压力。

图3 阀控非对称液压缸原理图
Fig. 3 Schematic diagram of valve controlled asymmetric cylinder
非对称液压缸最低固有频率在 位置处,选取此点进行建模,其中,
位置处,选取此点进行建模,其中, 为活塞杆无杆腔长度;
为活塞杆无杆腔长度; 为活塞杆有效行程;
为活塞杆有效行程; 为活塞杆有杆腔与无杆腔面积之比。
为活塞杆有杆腔与无杆腔面积之比。
液压动力元件建模分为阀的流量方程、液压缸流量方程以及力平衡方程[16]。
伺服阀流量方程为
 (4)
(4)
式中: 为负载流量;
为负载流量; 为伺服阀阀芯位移;
为伺服阀阀芯位移; 为负载压力;
为负载压力; 为伺服阀的流量增益;
为伺服阀的流量增益; 为伺服阀的流量-压力系数。
为伺服阀的流量-压力系数。
非对称液压缸流量方程为
 (5)
(5)
式中: 为系统泄漏系数;
为系统泄漏系数; 为油缸总泄漏系数;
为油缸总泄漏系数; 为液压缸有效容积;
为液压缸有效容积; 为液压油体积弹性模量;
为液压油体积弹性模量; 为负载压力变化率;
为负载压力变化率; 为活塞杆位移;
为活塞杆位移; 为活塞杆速度。
为活塞杆速度。
非对称液压缸负载力平衡方程为
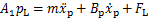 (6)
(6)
式中: 为负载与活塞杆折算到活塞上的总质量;
为负载与活塞杆折算到活塞上的总质量;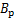 为负载与活塞杆的黏性阻尼系数;
为负载与活塞杆的黏性阻尼系数; 为活塞杆上的外负载力;
为活塞杆上的外负载力; 为活塞杆加速度。
为活塞杆加速度。
对式(4)~(6)进行拉氏变换,得
 (7)
(7)
根据式(7)建立单通道伺服阀控非对称液压缸的方框图,如图4所示,图4中, 为总流量-压力系数,其中,
为总流量-压力系数,其中, 。由图4可见:空载流量部分用于活塞运动消耗,剩余的流量在压缩和泄漏的作用下产生负载压力,进而作用于活塞面积上,驱动外部负载。
。由图4可见:空载流量部分用于活塞运动消耗,剩余的流量在压缩和泄漏的作用下产生负载压力,进而作用于活塞面积上,驱动外部负载。

图4 阀控非对称液压缸方框图
Fig. 4 Block scheme of valve control asymmetric hydraulic cylinder
1.3 系统整体建模
EH-MDLPM上平台与伺服阀控非对称液压缸活塞杆可视为刚性连接,并且 和
和 中分别包括上平台与活塞杆映射至关节空间中的质量项与重力项,因此,力平衡方程可重新写为
中分别包括上平台与活塞杆映射至关节空间中的质量项与重力项,因此,力平衡方程可重新写为
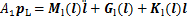 (8)
(8)
高频响伺服阀在0.5 Hz以内的低频段工作时,控制信号与伺服阀阀芯位移的传递关系可视为比例环节,表示为
 (9)
(9)
式中: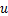 为伺服阀驱动电信号;
为伺服阀驱动电信号;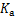 为伺服阀放大系数。
为伺服阀放大系数。
由式(8)可知:6套阀控非对称液压缸的输出力组成的力矢量即为EH-MDLPM动力学模型的输入力矢量。因此,结合图2和图4,即可得到EH-MDLPM在关节空间中的整体力控模型,如图5所示,其中6个通道采用规格型号相同的伺服阀与非对称液压缸,具有相等的性能参数,被视为常数项的 与干扰项的
与干扰项的 没有加入方框图中。
没有加入方框图中。

图5 液驱并联机构多维力加载系统模型
Fig. 5 Model of electro-hydraulic multi-dimensional force loading system with parallel mechanism
2 系统耦合分析
根据式(7)可以得到阀控非对称液压缸输出力为
 (10)
(10)
式中: 为单位矩阵。
为单位矩阵。
结合式(8)~(10)可得,在各位姿下阀控非对称液压缸输出力 为
为

 (11)
(11)
式中: 为驱动信号到阀控非对称液压缸输出力的传递函数。
为驱动信号到阀控非对称液压缸输出力的传递函数。
由式(11)可知:映射至关节空间的质量矩阵和刚度矩阵为非对角阵,在进行多维力加载过程中第 通道的控制信号会影响第
通道的控制信号会影响第 通道的输出力,因此,EH-MDLPM存在动力学耦合。
通道的输出力,因此,EH-MDLPM存在动力学耦合。
结合关节空间单通道力闭环P控制,系统的闭环传递函数可表示为
 (12)
(12)
式中: 为控制器矩阵;
为控制器矩阵; 为各支腿指令的力矢量。
为各支腿指令的力矢量。
由式(12)可知, 与
与 均不是对角阵,在自由度空间中,由输出力
均不是对角阵,在自由度空间中,由输出力 到输入指令
到输入指令 的传递函数矩阵中系数项不是对角阵。因此,在进行多维力加载时,各通道之间存在严重的输出力耦合现象[17]。
的传递函数矩阵中系数项不是对角阵。因此,在进行多维力加载时,各通道之间存在严重的输出力耦合现象[17]。
3 滑模控制改进及其稳定性分析
3.1 名义模型计算
为了进行多维力加载系统的滑模控制器设计,首先需知其名义模型,名义模型所需的有关参数如表1所示。
表1 多维力加载系统名义模型参数
Table 1 Nominal model of multi-dimensional force loading system

EH-MDLPM上平台和阀控非对称液压缸映射至关节空间中的实际质量矩阵与弹性负载映射至关节空间中的实际刚度矩阵不能准确获得,但EH-MDLPM各部分的方程形式是相同的。式(3)所表达的机理模型中实际质量阵 和实际刚度阵
和实际刚度阵 与二者各自对应的名义质量阵
与二者各自对应的名义质量阵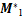 和名义刚度阵
和名义刚度阵 并不相同,但其相应的各元素数值大致接近,用
并不相同,但其相应的各元素数值大致接近,用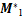 和
和 对系统传递函数分子项补偿,并作为滑模控制器设计的名义模型,从而降低设计难度,并起到滤波作用。因此,把系统
对系统传递函数分子项补偿,并作为滑模控制器设计的名义模型,从而降低设计难度,并起到滤波作用。因此,把系统 与
与 的传递函数简化为
的传递函数简化为

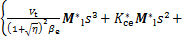

 (13)
(13)
式中: 为整体模型(分子项补偿前和补偿后)驱动信号。式(13)可进一步简化为
为整体模型(分子项补偿前和补偿后)驱动信号。式(13)可进一步简化为


 (14)
(14)
其中:
 (15)
(15)
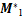 为上平台和活塞杆映射至关节空间中的名义质量矩阵;
为上平台和活塞杆映射至关节空间中的名义质量矩阵; 为弹性负载映射至关节空间的名义刚度矩阵;
为弹性负载映射至关节空间的名义刚度矩阵; 为名义总流量-压力系数;
为名义总流量-压力系数; 为伺服阀的名义流量增益;
为伺服阀的名义流量增益; 为关节空间的实际质量矩阵与名义质量矩阵的误差;
为关节空间的实际质量矩阵与名义质量矩阵的误差;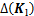 为关节空间的实际刚度矩阵与名义刚度矩阵的误差;
为关节空间的实际刚度矩阵与名义刚度矩阵的误差; 为实际矩阵取逆与矩阵误差的乘积。
为实际矩阵取逆与矩阵误差的乘积。
 有界,假设
有界,假设 ,式中:
,式中: 为常数矩阵。
为常数矩阵。
定义
 (16)
(16)
其中,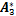 ,
, ,
, 和
和 分别为通过理论计算得到的名义值。
分别为通过理论计算得到的名义值。
将式(16)代入式(14),式(14)可以重新写为
 (17)
(17)
式中: 为
为 的
的 阶导数。
阶导数。
根据式(17)进行滑模控制器设计。与式(17)方程形式相似,加入分子项补偿的理论模型为
 (18)
(18)
 (19)
(19)
其中, ,
, ,
, 和
和 分别为通过实验得到的实际值。
分别为通过实验得到的实际值。
EH-MDLPM是三阶单输入单输出的非线性系统,结合文献[18-19]设计滑模控制器。第 个通道的滑模控制器设计过程如下所示。结合式(18),定义
个通道的滑模控制器设计过程如下所示。结合式(18),定义
 (20)
(20)
式中: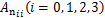 为
为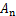 的各对角元素。
的各对角元素。
3.2 控制器设计
第 个通道力跟踪误差
个通道力跟踪误差 为
为
 (21)
(21)
式中: 为第
为第 通道的输出力矢量;
通道的输出力矢量; 为第
为第 通道的指令力矢量。
通道的指令力矢量。
定义第 个通道滑模面为
个通道滑模面为
 (22)
(22)
 (23)
(23)
 (24)
(24)
 (25)
(25)
式中: (
( ,1,2,3)为
,1,2,3)为 的
的 阶导数;
阶导数; 为第
为第 通道滑模控制器的控制矩阵;
通道滑模控制器的控制矩阵; 和
和 分别是第
分别是第 通道滑模控制器的控制参数;
通道滑模控制器的控制参数; 和
和 决定力跟踪误差的收敛速度。调整参数
决定力跟踪误差的收敛速度。调整参数 和
和 ,极点离复平面虚轴越远,系统到滑模面时间越短。
,极点离复平面虚轴越远,系统到滑模面时间越短。
根据线性化反馈技术,结合所设计的名义模型和滑模面,第 个通道滑模控制律可设计为
个通道滑模控制律可设计为
 (26)
(26)
其中,
 (27)
(27)
 (28)
(28)
式中: 为
为 的
的 阶导数;
阶导数; 为第
为第 个通道的切换增益;
个通道的切换增益; 为滑模面的符号函数。
为滑模面的符号函数。
结合式(18),(20)和(26),第 个通道滑模控制律为
个通道滑模控制律为

 (29)
(29)
式中: 为第
为第 个通道滑模面的符号函数。
个通道滑模面的符号函数。
由式(29)可知,增大切换增益 导致伺服阀电信号的抖振增大。
导致伺服阀电信号的抖振增大。
3.3 稳定性分析
根据式(21)可得
 (30)
(30)
式中: 为
为 的
的 阶导数。
阶导数。
当名义模型与实际模型的输出力相等时,将式(29)和(30)代入式(17)可得到如下关系式:


 (31)
(31)
式中: 为
为 的各对角元素;
的各对角元素; 为
为 的各对角元素。
的各对角元素。
对式(22)求导, 的表达式为
的表达式为
 (32)
(32)
式中: 为
为 的一阶导数。
的一阶导数。
将式(32)代入式(31),可得

 (33)
(33)
其中:
 (34)
(34)
令

 (35)
(35)
由式(34)可知, ,
, ,
, 和
和 均为有界的建模误差;
均为有界的建模误差; 为第
为第 个通道滑模控制律的建模误差,可得建模误差
个通道滑模控制律的建模误差,可得建模误差 有界。由于输出力的导数与输出力频率有关,因此,增大输出力的频率会导致
有界。由于输出力的导数与输出力频率有关,因此,增大输出力的频率会导致 数值增大。
数值增大。
将式(35)代入式(33), 可以重新写为
可以重新写为
 (36)
(36)
设Lyapunov函数为
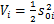 (37)
(37)
结合式(36)和式(37)可得,Lyapunov函数的一阶导数为
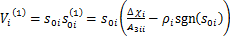 (38)
(38)
由式(38)可得,当 时,
时, 恒成立。
恒成立。
从改进的滑模控制稳定性条件可知,当切换增益 大于不确定边界时,滑模控制器的控制律
大于不确定边界时,滑模控制器的控制律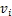 可接近滑模面。当
可接近滑模面。当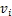 沿滑模面移动时,
沿滑模面移动时, 趋于0。此时,
趋于0。此时, 和
和 越大,
越大, 越小,从而保证了动态力跟踪精度。
越小,从而保证了动态力跟踪精度。
EH-MDLPM各力加载通道间存在耦合力,耦合力可以被视为是一种干扰[20],由式(38)可以看出,滑模控制减轻控制信号的抖动现象,降低干扰的影响,提高动态跟踪性能。
4 实验验证
4.1 实验方案
液驱并联机构多维力加载系统由机械结构、液压系统和控制系统3部分组成。机械结构主体采用Stewart平台,选取伺服阀控非对称缸驱动。控制系统采用基于Matlab/xPC Target的快速原型控制技术,其组成如图6所示,上位机和下位机分别采用PC机与工控机。在上位机中采用MATLAB/Simulink软件搭建模型与编写程序并编译为C语言,通过网线将上位机中编译的代码传输至下位机中运行。下位机装有AD和DA板卡,位移传感器、拉压力传感器与六维力传感器采集的信号经调理输入到AD板卡,DA板卡输出信号经调理至伺服阀,形成闭环系统,且上位机实时监控系统运行状态。

图6 实验方案
Fig. 6 Experimental scheme
4.2 实验结果
4.2.1 PI控制
在PI控制作用下,当向Fx和Fy自由度力加载通道方向各输入400 N/0.5 Hz的正弦力信号,向Fz自由度力加载通道方向输入0 N的力信号,向Rx和Rz自由度力加载通道方向各输入50 N·m/0.5 Hz的正弦力矩信号,向Ry自由度力加载通道方向输入0 N·m的力矩信号时,调整PI控制器参数,使力加载跟踪性能达到最佳,此时,各自由度方向力加载通道的力加载跟踪性能曲线如图7所示。

图7 PI控制各自由度力加载通道跟踪曲线
Fig. 7 Tracking curve of each force loading channel by PI control
由图7可见:在PI控制作用下,其他自由度通道对Fz自由度力加载通道产生范围为-192~251.8 N的耦合力,其他自由度通道对Ry自由度力加载通道产生范围为-11.5~14.1 N·m的耦合力矩。Fx自由度力加载通道的力跟踪曲线存在一定幅值衰减,Rx和Rz自由度力加载通道呈现较大的相位滞后,并且受到其他自由度通道对其产生的耦合力影响,导致Rx自由度力加载通道的力矩跟踪范围扩大到-71.8~63.3 N·m,Rz自由度力加载通道的力矩跟踪范围值扩大到-48.8~79.7 N·m。因此,EH-MDLPM各自由度存在严重的耦合力,并且在动态跟踪过程中存在幅值衰减和相位滞后现象。
4.2.2 滑模控制
在滑模控制作用下,当向Fx和Fy自由度力加载通道方向各输入400 N/0.5 Hz的正弦力信号,向Fz自由度力加载通道方向输入0 N的力信号,向Rx和Rz自由度力加载通道方向各输入50 N·m/0.5 Hz的正弦力矩信号,向Ry自由度力加载通道方向输入0 N·m的力矩信号时,调整滑模控制器参数,使力加载跟踪性能达到最佳,此时,各自由度方向力加载通道的力加载跟踪性能曲线如图8所示。

图8 滑模控制各力加载通道跟踪曲线
Fig. 8 Tracking curve of each force loading channel by sliding mode control
由图8可见:在滑模控制作用下,其他自由度通道对Fz自由度力加载通道产生范围为-32.3~27.7 N的耦合力,其他自由度通道对Ry自由度力加载通道产生范围为-3.8~4.9 N·m的耦合力矩。与PI控制器相比,Fz自由度力加载通道的耦合力范围缩小86.5%,Ry自由度力加载通道的耦合力矩范围缩小66%,Fx自由度力加载通道的力跟踪曲线幅值衰减得到改善,Fy自由度力加载通道的动态跟踪性能得到提高,Rx和Rz自由度加载通道的力矩跟踪曲线相位滞后得到改善,受到其他自由度通道对其产生的耦合力影响减小。
通过以上多维力加载实验可知,在滑模控制器下EH-MDLPM的耦合力降低,耦合力干扰受到抑制,从而实现解耦,并且动态跟踪性能得到提高。
5 结论
1) 提出了一种改进的滑模控制算法,该算法有效降低了系统参数时变与模型摄动对EH-MDLPM控制精度的影响。
2) 建立了机构动力学模型,系统广义质量和广义刚度为非对角阵是导致EH-MDLPM各通道间输出力耦合的主要因素。
3) 通过Lyapunov理论分析了改进的滑模控制结构的稳定性,与切换增益、机构参数、液压缸参数及伺服阀参数相关的稳定条件,即  。
。
4) 与PI控制相比,改进的滑模控制耦合力减小了86.5%,耦合力矩减小了66%,提高了系统动态响应速度与输出精度。
参考文献:
[1] 谭健. Stewart 并联机构特性及自适应控制研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2015: 1-7.
TAN Jian. Research on mechanism characteristic and adaptive control of Stewart platform[D]. Harbin: Harbin Institute of Technology. School of Mechatronics Engineering, 2015: 1-7.
[2] 王东炜. Stewart 平台隔振的主动控制研究[D]. 哈尔滨: 哈尔滨工业大学航天学院, 2014: 2-6.
WANG Dongwei. Study on active control of Stewart platform for vibration isolation[D]. Harbin: Harbin Institute of Technology. School of Astronautics, 2014: 2-6.
[3] 侯立果, 王丹, 安大卫, 等. 多维力加载装置动力学建模及加载试验[J]. 北京航空航天大学学报, 2018, 44(5): 1095-1101.
HOU Liguo, WANG Dan, AN Dawei, et al. Dynamic modeling and loading experiment of multi-dimensional loading device[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(5): 1095-1101.
[4] 高征, 郭钰莹, 苏锐, 等. 4-Stewart并联平台的运动学分析[J]. 机械设计与制造, 2018(6): 37-40.
GAO Zheng, GUO Yuying, SU Rui, et al. Kinematics analysis of a 4-Stewart parallel platform[J]. Machinery Design & Manufacture, 2018(6): 37-40.
[5] 文刚, 高宏力, 彭志文, 等. Stewart并联机器人控制算法研究[J]. 机械设计与制造, 2018(8): 226-228, 232.
WEN Gang, GAO Hongli, PENG Zhiwen, et al. Research of Stewart parallel robot control algorithm[J]. Machinery Design & Manufacture, 2018(8): 226-228, 232.
[6] MURRAY J A, SASANI M, SHAO Xiaoyun. Hybrid simulation for system-level structural response[J]. Engineering Structures, 2015, 103: 228-238.
[7] 王辉, 许守林, 冯英进, 等. 飞行模拟器操纵负荷力加载控制系统的试验研究[J]. 中国机械工程, 2008, 19(14): 1720-1723.
WANG Hui, XU Shoulin, FENG Yingjin, et al. Testing research for control loading system of flight simulator[J]. China Mechanical Engineering, 2008, 19(14): 1720-1723.
[8] 王博, 黄其涛. 正交并联多自由度加载试验系统研究[J]. 机电工程, 2016, 33(11): 1334-1338.
WANG Bo, HUANG Qitao. Loading test system of orthogonal parallel multi-degree-of-freedom[J]. Journal of Mechanical & Electrical Engineering, 2016, 33(11): 1334-1338.
[9] UKIDVE C S, MCINROY J E, JAFARI F. Orthogonal Gough-Stewart platforms with optimal fault tolerant manipulability[C]// Proceedings 2006 IEEE International Conference on Robotics and Automation, 2006. ICRA 2006. 2006, Orlando, USA. IEEE, 2006: 3801-3806.
[10] YANG Guilin, CHEN Iming, CHEN Weihua, et al. Kinematic design of a six-DOF parallel-kinematics Machine with decoupled-motion architecture[J]. IEEE Transactions on Robotics, 2004, 20(5): 876-887.
[11] 赵春红, 张洛平. 用于驱动液压缸活塞运动轨迹跟踪的二阶滑模控制[J]. 中国工程机械学报, 2019, 17(4): 311-315.
ZHAO Chunhong, ZHANG Luoping. Two order sliding mode control for driving trajectory tracking of hydraulic cylinder piston[J]. Chinese Journal of Construction Machinery, 2019, 17(4): 311-315.
[12] 张达, 原大宁, 刘宏昭. 考虑关节摩擦的3-UPS/PU并联机构模糊自适应滑模控制[J]. 中国机械工程, 2017, 28(4): 391-397, 403.
ZHANG Da, YUAN Daning, LIU Hongzhao. Adaptive fuzzy sliding mode control of 3-UPS/PU parallel mechanisms including joint frictions[J]. China Mechanical Engineering, 2017, 28(4): 391-397, 403.
[13] 刘希, 黄茹楠, 高英杰. 电液位置伺服系统自适应反演滑模控制[J]. 液压与气动, 2019(7): 14-19.
LIU Xi, HUANG Runan, GAO Yingjie. Adaptive inversion sliding mode control for electro-hydraulic servo motion system[J]. Chinese Hydraulics & Pneumatics, 2019(7): 14-19.
[14] 黄道敏, 韩丽君, 唐国元, 等. 水下机械手分数阶积分滑模轨迹跟踪控制方法研究[J]. 中国机械工程, 2019, 30(13): 1513-1518.
HUANG Daomin, HAN Lijun, TANG Guoyuan, et al. Fractional integral sliding mode control for trajectory tracking of underwater manipulators[J]. China Mechanical Engineering, 2019, 30(13): 1513-1518.
[15] 吴博. 基于定量反馈理论的飞行模拟器运动平台控制系统研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2007: 19-39.
WU Bo. Research on flight simulator motion platform control system based on quantitative feedback theory[D]. Harbin: Harbin Institute of Technology. School of Mechatronics Engineering, 2007: 19-39.
[16] 杨军宏. 三自由度船舶运动模拟平台及其液压伺服驱动系统的研究[D]. 长沙: 国防科学技术大学智能科学学院, 2007: 29-50.
YANG Junhong. Research on ship motion simulator with three degrees of freedom and its hydraulic servo driven system[D]. Changsha: National University of Defense Technology. School of Intelligent Science, 2007: 29-50.
[17] 董利伟. 广义并联机构可重构机理与耦合特性分析[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2016: 21-54.
DONG Liwei. Analysis on reconfiguration principle and coupling characteristics of generalized parallel mechanism[D]. Harbin: Harbin Institute of Technology. School of Mechatronics Engineering, 2016: 21-54.
[18] 刘金琨. 滑模变结构控制MATLAB仿真[M]. 北京: 清华大学出版社, 2005: 217-218.
LIU Jinkun. MATLAB Simulation for Sliding Mode Control[M]. Beijing: Tsinghua University Press, 2005: 217-218.
[19] SONG Junbo, ISHIDA Y. A robust sliding mode control for pneumatic servo systems[J]. International Journal of Journal of Engineering Science, 1997, 35(8): 711-723.
[20] 尹鹏. 基于并联机构的多自由度力加载系统研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2015: 52-60.
YIN Peng. Research on multi-degree of freedom force loading system based on parallel mechanism[D]. Harbin: Harbin Institute of Technology. School of Mechatronics Engineering, 2015: 52-60.
(编辑 秦明阳)
收稿日期: 2020 -02 -25; 修回日期: 2020 -04 -27
基金项目(Foundation item):国家自然科学基金资助项目(51505412);流体动力与机电系统国家重点实验室开放基金资助项目(GZKF-201807) (Project(51505412) supported by the National Natural Science Foundation of China; Project(GZKF-201807) supported by the State Key Laboratory of Fluid Power and Mechatronic Systems Open Fund Project)
通信作者:赵劲松,博士,副教授,从事电液伺服研究;E-mail:zhaojinsong@ysu.edu.cn