双边带调制信号间的互相关影响及分析
徐成涛,刘瀛翔,唐小妹,王飞雪
(国防科技大学 电子科学与工程学院,卫星导航研发中心,湖南 长沙,410073)
摘要:下一代卫星导航系统拟采用多种双频复用技术,如AltBOC和TD-AltBOC。复用信号之间的相关特性对接收机后端的信号处理部分将造成影响。同一颗卫星播发的下行导航信号,不同的信号分量始终具有相同的传播时延和动态特性,因此其互相关对伪距测量的影响是固定的。当信号间存在频差时双边带信号互相关对测距影响的研究较少。首先从信号接收的角度,给出双边带信号复用技术的简化模型。在此基础上,分析不同频信号互相关对伪码和载波跟踪的影响,最后通过仿真数据验证了结论的正确性。该结论也可以扩展至对不同频点间任意调制方式信号互相关影响的分析,对接收机信号处理环路的设计,以及系统信号体制的选择具有一定的指导意义。
关键词:双边带;多路复用;扩频码;互相关
中图分类号:TP967.1 文献标志码:A 文章编号:1672-7207(2014)04-1098-07
Analysis for cross correlation in dual band modulation signals
XU Chengtao, LIU Yingxiang, TANG Xiaomei, WANG Feixue
(Satellite Navigation Research and Development Center, School of Electronic Science and Engineering,
National University of Defense Technology, Changsha 410073, China)
Abstract: Several Dual Band Modulation multiplexing techniques will be utilized in the next generation Global Navigation Satellite System, like AltBOC and TD-AltBOC. Correlation properties between multiplexed signals may have influence on the signal processing part of the receiver. The propagation delay and motion characteristic of different signals broadcast from one satellite are always the same; therefore the cross correlation of these signals is time-invariant, causing an unchangeable pseudorange measuring bias. However, little research attention is drawn on this issue when there is frequency difference between correlated signals. A simplified model of Dual Band Modulation Signals in terms of signal receiving is introduced, based on which the influence on signal tracking from the cross correlation of dual band modulated signals is theoretically analyzed. In the end, simulation test is given to support the results. Similarly, the conclusion can be applied to the analysis of cross correlation between signals with different frequencies. Moreover, the conclusion can provide some insight into the system signal design and receiver tracking loop design.
Key words: dual band; multiplexing; spread code; cross correlation
卫星导航接收机的测距误差受很多因素的影响,除了噪声和干扰,目前分析较多的误差来源包括卫星、接收机的钟差、电离层延迟、对流层延迟、星历预测误差和多径误差[1]。卫星导航信号体制的发展体现出向多个频段、多类服务、多种调制方式的复杂化趋势。在信号层,出现了新型的导航信号调制方式和复用方式,包括三路信号复用的Interplex调制[2]和CASM调制[3],四路信号复用的AltBOC[4],TD-AltBOC[5]和Dual QPSK[6]调制、不限定信号路数的POCET调制[7]。对信号间的相关特性引起的干扰分析,多见于对多址干扰的分析。一般认为,同一频点的不同卫星信号扩频码之间的多址干扰对伪距测量的影响较小。但是李星等[8]指出,在特殊情况下,多址干扰形成的伪码跟踪误差是不可忽略的。而对于同一颗卫星播发的下行导航信号,由于同一卫星的不同信号分量始终具有相同的传播时延和动态特性,因此,其互相关对伪距测量的影响是固定的,即在任何情况下都可能存在[9]。故相比于多址干扰,互相关会对信号跟踪产生恒定的影响。但目前还没有文献对这类问题进行全面的分析。文献[9]对同频的复用信号互相关的影响进行了研究和分析,指出同频同相的互相关信号将造成一定的互相关影响,其在精密测距场景下带来的误差不可忽略。本文作者通过研究指出不同频信号引入的互相关对伪距测量值的影响,相比于同频复用信号的互相关是不可忽略的。因此,对于卫星导航系统新体制下广泛采用的双边带信号如BOC,AltBOC和TD-AltBOC等宽带调制信号,采用单边带接收方式时需要考虑对称边带信号引入的互相关问题[10-12]。本文作者首先给出用于信号处理的简化信号模型,然后对双边带调制信号对接收机跟踪环路积分结果和测距误差结果的影响进行分析,最后对前述的理论分析进行仿真测试,验证双边带信号的互相关确实对信号伪距测量有不利影响,在原有的测距误差基础上加入系统偏差。并说明在动态环境下,上述结论依然成立。
1 信号模型
不同复用方式的信号解析表达式存在较大的差异,且相对复杂[13]。根据文献[9],本文主要考虑双边带调制信号,即载波频率不相等的情况。
综合上述分析后,可以将多路复用信号简化为
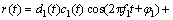
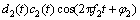 (1)
(1)
其中:φ表示两路载波间的相对相位关系;f1表示目标信号分量的载波频率;f2表示互相关信号分量的载波频率;di(t)表示第i路信号上调制的电文;ci(t)表示第i路信号上调制的测距码。
在上述模型的基础上,分析频间互相关对信号跟踪的影响。下面将c1(t)信号称为目标信号,c2(t)信号称为互相关信号。
1.1 环路相关器模型
由于接收机一般利用伪距测量值实现定位功能,设接收机已精确复现出接收信号的频率,接收机生成的本地复现码与接收信号之间码相位延迟为τ,早迟码间隔为2δ,则本地信号和中频信号相干积分的结果为
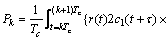
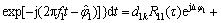

 (2)
(2)
其中: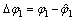 ;
;
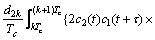
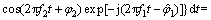
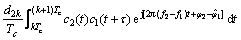 (3)
(3)
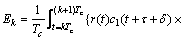
 (4)
(4)
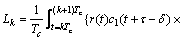
 (5)
(5)
其中:Ek,Pk和Lk分别表示时刻k对应的提前、即时和滞后支路的相关值,包括同相和正交分量;d1k和d2k分别表示时刻k对应的电文;Tc表示预检测积累时间;R11(τ)表示测距码c1(t)的自相关函数;R12(τ)表示测距码c1(t)与c2(t)的互相关函数;设△f=f2-f1,则根据△f与积分时间Tc和伪码速率之间的关系,积分式得到不同的结果。
1.2 鉴别器输出
伪码跟踪环路使用非相干EMLP(提前减滞后功率)鉴别器[14]
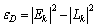 (6)
(6)
载波跟踪环路使用Costas环[15]——二象限反正切鉴相器,鉴相器输出为
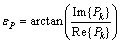 (7)
(7)
由式(6)和(7)可知:当互相关幅度相比自相关幅度可以忽略时,载波环和码环稳定的条件为θ=0和τ=0,即载波环和码环可以无偏地估计出接收信号的载波相位和伪码相位。
2 非同频信号的互相关特性
2.1 当△f=0时
该情况下,互相关的影响等于同频信号分量之间互相关的影响,分析结果见文献[9]。
此时,DLL环路相干积分的结果将受到信号间的互相关部分的干扰。
2.2 当△f<<1/Tc时
此时,载波差频项在积分时间内的变化缓慢,则载波差频项可以从积分式中分离[16],有

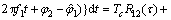
 (8)
(8)
其中: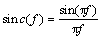 。则积分结果化简为
。则积分结果化简为
 (9)
(9)
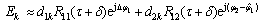 (10)
(10)
 (11)
(11)
在该情况下,互相关的影响等于同频信号分量之间互相关的影响。与同频信号互相关影响的结果类似,此时DLL环路相干积分的结果将受到信号间的互相关部分的干扰。
2.3 当△f>>max(fcode)时
此时,载波差频项在伪码码片内快速变化,扩频码在差频项的周期内变化缓慢。则可将积分时间分割为载波差频项周期之和,在该周期内的相干积分为0。则积分器的输出为
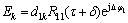 (12)
(12)
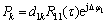 (13)
(13)
 (14)
(14)
2.4 当△f属于其他情况时
此时,载波差频与积分时间的倒数可相互比较。此时,该积分不能化简。

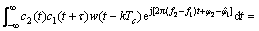
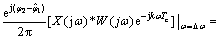
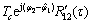 (15)
(15)
其中:
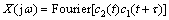 (16)
(16)
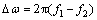 (17)
(17)
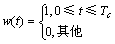 (18)
(18)
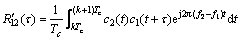 (19)
(19)
进一步化简为
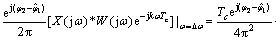
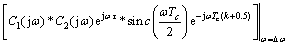 (20)
(20)
式中:C(jω)为信号的频谱;*表示线性卷积;R′12(τ)代表广义下的互相关积分。
值得注意的是,当△f·Tc为整数时,广义互相关积分与积分时段k无关,若△f·Tc不为整数,则广义互相关积分在不同积分时段k下存在相位偏转,目标信号遭受的互相关影响随时间变化:
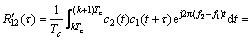
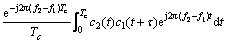
该相位偏转可归为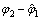 的变化。在该情况下,相干积分的互相关部分可以表示为信号频谱与窗函数频谱的卷积结果当频率等于互相关信号间频率差时的值。
的变化。在该情况下,相干积分的互相关部分可以表示为信号频谱与窗函数频谱的卷积结果当频率等于互相关信号间频率差时的值。
 (21)
(21)
 (22)
(22)
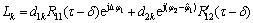 (23)
(23)
同样的,DLL环路相干积分的结果将受到信号间的互相关部分的干扰,由于信号间的互相关无显式的解析表达式,因此互相关干扰的程度需要采用仿真的方法得到积分的结果。
图1和图2所示为归一化广义互相关积分仿真曲线,其中fc为码率。从图1和图2的仿真结果可见:广义下的互相关积分R′12(τ)有以下几个特征:(1) 跟踪偏差小于0.5个码片时,互相关积分相比于自相关小1至2个量级;(2) 互相关积分随频差的变化没有明显的规律可循,不同频差下的互相关积分变化不大;(3) 通过扩频码的设计,可改善零频下的互相关积分,但广义互相关积分的改善不明显。

图1 归一化广义互相关积分仿真曲线(PRN1与PRN5)
Fig. 1 Simulation curve of generalized cross correlation (PRN1 vs. PRN5)
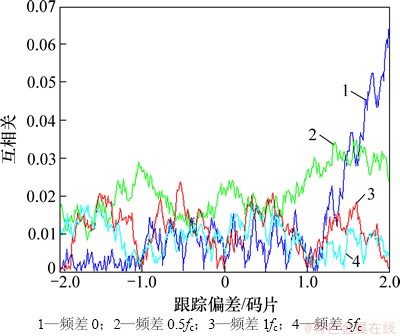
图2 归一化广义互相关积分仿真曲线(PRN1与PRN2)
Fig. 2 Simulation curve of generalized cross correlation (PRN1 vs. PRN2)
根据前面对信号模型和延迟锁定环路相干积分结果的分析,可知根据目标信号与相关信号中心频率之间的关系,相关器的输出结果随之变化。其中,对情况1和3的分析已经在文献[1, 14-15]中论述,而情况2等价于情况1,下面只考虑情况4下互相关对跟踪环路的影响。
3 非同频互相关对跟踪的影响
码环稳定跟踪时,根据前面的分析,当互相关幅度相比自相关幅度不可忽略时,即除互相关信号的频差远大于信号码率的情况外,互相关信号都将对信号的相关结果产生一定的影响,而一般情况下互相关无法解析表示,因此,无法得到DLL环路中鉴相器的码相位延迟τ0的解析解,但是,仍可分析码相位延迟的近似解及其变化规律。
鉴别器输出可以分解为自相关项εa和互相关项εc之和,存在互相关信号时,鉴别器的输出等于互相关引入的偏差。不妨设载波环准确跟踪(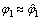 ),则
),则
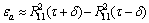 (24)
(24)
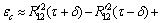
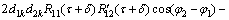
 (25)
(25)
自相关函数可近似表示为:
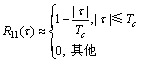 (26)
(26)
其中:Tc为码片宽度。可以将信号间的相位关系分为3种情况:φ=0,例如理想情况下TD-AltBOC调制中任意2个的信号分量;φ=π/2,例如理想情况下AltBOC调制中相同边带的信号分量;φ为其他值。在一般情况下,但是由于色散效应和前面的分析,非同频间的相位差是不可预知的。
当φ2-φ1=π/2时,因为τ0<<δ,因此,码跟踪偏差可以根据下式近似得到:
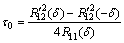 (27)
(27)
由式(27)可知:当φ2-φ1=π/2,码跟踪偏差仅和自相关、广义互相关、早迟码间隔有关。
当φ2-φ1=0时,同样可以得到该条件下码跟踪偏差的解析表达式:
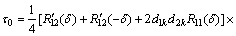
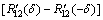 (28)
(28)
由式(28)可知:当φ2-φ1=0,码跟踪偏差不仅和互相关、早迟码间隔有关,还和调制的电文符号有关。
当φ2-φ1为其他任意值时,码跟踪偏差近似为

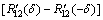 (29)
(29)
由式(29)可知:此时码跟踪偏差不仅与互相关、早迟码间隔有关,还与调制的电文符号有关。
根据上述结论可知:互相关引入的伪码相位偏差和电文符号有关。由于真实环境中导航电文在一定的时间段内具有一定的周期性,因此,会造成伪码相位偏差存在和导航电文周期一致的周期性的波动。
当载波环稳定跟踪时,载波相位偏差的近似解为
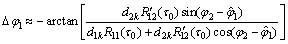 (30)
(30)
由式(30)可知:载波相位偏差与自相关幅度、互相关幅度、电文符号和载波相位差均有关系。当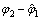 =0,载波相位偏差近似为0。
=0,载波相位偏差近似为0。
稳定跟踪时,τ0固定,若此时R′12(τ0)=0,则载波相位偏差近似为0。否则,当满足以下条件载波相位偏差最大。
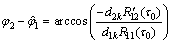 (33)
(33)
从上面的分析可见:互相关引入的载波相位偏差主要与互相关有关,当目标信号和互相关信号载波同向时互相关对载波相位偏差的影响可以忽略。
4 仿真验证
下面使用matlab仿真验证上述的结论,具体的仿真参数如表1所示。
分别仿真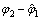 =0和
=0和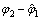 =π/2这2种情况。具体的仿真结果如图3和4所示。
=π/2这2种情况。具体的仿真结果如图3和4所示。
由图3和4可见:
(1) 当互相关信号与目标信号存在可与码率相比拟的频差时,双边带调制信号的伪码相位偏差仍然存在,且相比同频情况没有明显的下降趋势,甚至可能增大;
(2) 同频时,TD-AltBOC调制的伪码相位偏差明显大于AltBOC。当存在频差时,TD-AltBOC调制的伪码相位偏差和AltBOC调制的伪码相位偏差的关系无规律可循。
(3) φ2-φ1=π/2时,伪码跟踪偏差随电文比特变化而波动,这是由于互相关造成误差引起了目标信号相干积分跨越了电文比特翻转时刻,因此,使得码环不断地进行调整。通过降低环路带宽增强滤波效果,可以减少电文比特翻转带来的影响。该波动是由互相关间接造成的,但互相关影响较小时,波动不明显,因此,信号同频时无明显波动。当φ2-φ1=0时,由于电文符号直接影响鉴别器输出,因此,信号同频时依然存在跟踪偏差随电文波动的情况。
表1 仿真参数列表
Table 1 List of simulation parameter
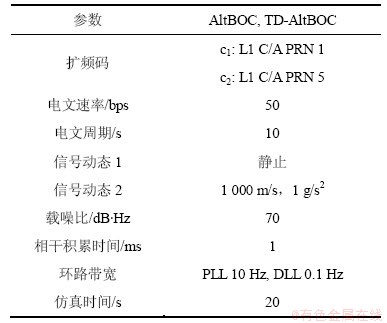
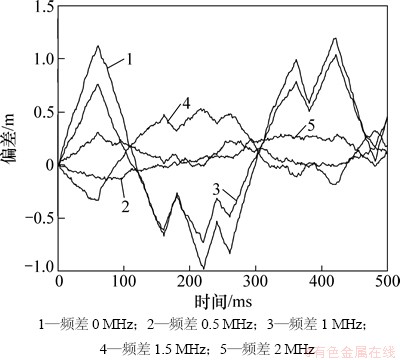
图3 TD-AltBOC调制中c1(t)信号的码相位跟踪偏差(φ2-φ1=0)
Fig. 3 Track bias of c1(t) using TD-AltBOC modulation (φ2-φ1=0)
将AltBOC的互相关信号的c2(t)替换为PRN2,仿真结果如图5和6所示。
由图5和6可见:对于同相或正交的信号,通过选择同频下互相关性能更加优异的扩频码,在互相关信号与目标信号存在一定频差的情况下,不易减小互相关引入的伪码相位偏差。上述结果与前面对广义下的互相关积分分析结果是一致的。

图4 AltBOC调制中c1(t)信号的码相位跟踪偏差(φ2-φ1=π/2)
Fig. 4 Track bias of c1(t) using AltBOC modulation (φ2-φ1=π/2)
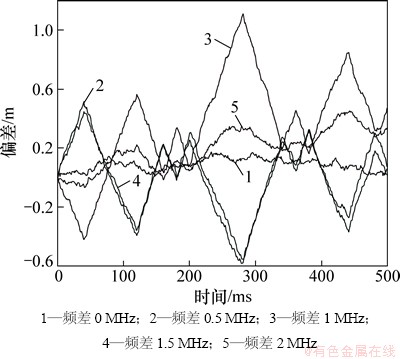
图5 扩频码更换后TD-AltBOC调制中c1(t)信号的静态条件下码相位跟踪偏差
Fig. 5 Track bias of c1(t) using TD-AltBOC modulation with different spread codes in static situation
卫星信号动态的变化不会改变互相关和自相关之间的相对关系,因此,互相关对码跟踪的影响与静态情况类似,仿真的结果如图7和8所示。
由图7和8可知:卫星信号动态的变化不会改变互相关信号引入的跟踪偏差,因此,上述结论对实际环境中的动态信号同样适用。

图6 扩频码更换后AltBOC调制中c1(t)信号的静态条件下码相位跟踪偏差
Fig. 6 Track bias of c1(t) using AltBOC modulation with different spread codes in static situation
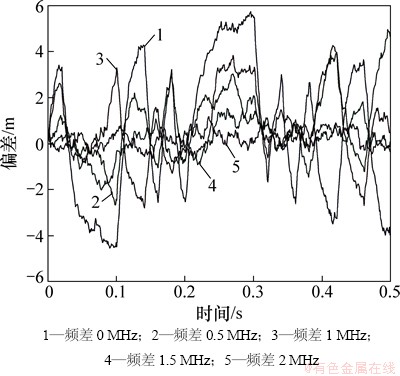
图7 扩频码更换后TD-AltBOC调制中c1(t)信号的动态条件下码相位跟踪偏差
Fig. 7 Track bias of c1(t) using TD-AltBOC modulation with different spread codes in dynamic situation
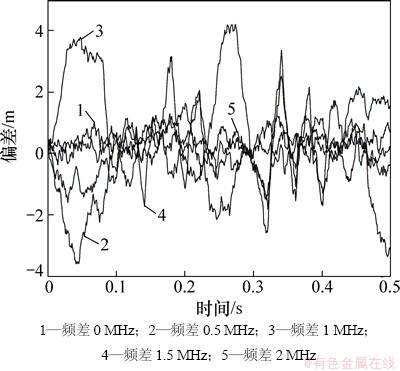
图8 扩频码更换后AltBOC调制中c1(t)信号的动态条件下码相位跟踪偏差
Fig. 8 Track bias of c1(t) using AltBOC modulation with different spread codes in dynamic situation
5 结论
(1) 随着双边带信号的频差变化会有不同的结果。在一般情况下,固定频差其互相关会引入一定的伪码跟踪偏差,而载波相位的变化对跟踪偏差的影响较小。此外,其他频点的信号进入中频数字处理环节后,其互相关同样会引入较大的伪码跟踪偏差。因此采用单边带方法处理双边带信号时,需要考虑来自对称边带信号的互相关干扰。
(2) 从减小互相关的影响角度来考虑,AltBOC调制与TD-AltBOC相比调制并不更具有优势。并且在选择双边带信号的扩频码时,需要根据其在±1个码片范围内的广义互相关值进行择优选择,以尽可能减小互相关对伪距测量的影响。该结论对卫星导航系统信号体制的选择和扩频码设计具有一定的指导意义。
参考文献:
[1] 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009: 78-90。
XIE Gang. Principles of GPS theory and receiver design[M]. Beijing: Publishing House of Electronics Industry, 2009: 78-90。
[2] Butman S, Timor U. Interplex: An efficient multichannel PSK/PM telemetry system[J]. IEEE Trans Communication, 1972, 20(3): 415-419.
[3]  J A. On generalized signal waveforms for satellite navigation[D]. Munich: University FAF Munich. Faculty of Aerospace Engineering, 2008: 288-290.
J A. On generalized signal waveforms for satellite navigation[D]. Munich: University FAF Munich. Faculty of Aerospace Engineering, 2008: 288-290.
[4] Lestarquit L, Artaud G, Issler J. AltBOC for dummies or everything you always wanted to know about AltBOC[C]//Proceedings of 21st International Technical Meeting of the Satellite Division of the Institute of Navigation. Savannah, GA, USA, 2008: 961-970.
[5] TANG Zuping, ZHOU Hongwei, WEI Jiaolong, et al. TD-AltBOC: A new COMPASS B2 modulation[J]. Science China: Physics, Mechanics & Astronomy, 2011, 54(6): 1014-1021.
[6] ZHANG Kai. A signal generation method of Dual QPSK: China, 201110451739.0[P]. 2011-12-29.
[7] Dafesh P A, Cahn C R. Phase-optimized constant-envelope transmission (POCET) modulation method for GNSS signals[C]//Proceedings of 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation. Savannah, GA, USA, 2009: 2860-2866.
[8] 李星, 王飞雪, 欧刚, 等. 卫星导航系统中多址干扰引起的伪码跟踪误差的分析[J]. 信号处理, 2008, 24(5): 885-888.
LI Xing, WANG Feixue, OU Gang. Study on PN code tracking error caused by multi-user interference in satellite navigation system[J]. Signal Processing, 2008, 24(5): 885-888.
[9] LIU Yingxiang, TANG Xiaomei, WANG Feixue. Analysis for cross correlation in multiplexing[C]//China Satellite Navigation Conference (CSNC) 2013 Proceedings. Wuhan, China, 2013: 1-5.
[10] Shivaramaiah N C, Dempster A G. A novel extended tracking range DLL for AltBOC signals[C]//Vehicular Technology Conference Fall. Anchorage, Alaska, USA, 2009: 1-5.
[11] Shivaramaiah N C. Enhanced Receiver Techniques for Galileo E5 AltBOC Signal Processing [D]. Sydney: the University of New South Wales. Surveying & Spatial Information Systems, 2011: 40-46.
[12] Margaria D. Galileo AltBOC receivers: Analysis of receiver architectures, acquisition strategies and multipath mitigation techniques for the E5 AltBOC signal[D]. Turin: Polytechnic of Turin, Faculty of Engineering Information, 2007: 59-84.
[13] ZHANG Kai. Analytical transmission model of POCET technique for Compass B1 and B3 signals[C]//The 25th International Technical Meeting of the Satellite Division of The Institute of Navigation. Nashville, Tennessee, USA, 2012: 1-8.
[14] van Dierendonck A J. GPS receivers. The global positioning system: Theory and applications[M]. Washington: American Institute Aeronautics and Astronautics, 1996: 329-408.
[15] Kaplan E D, Hegarty C J. Understanding GPS principles and applications[M]. 2nd ed. Beijing: Publishing House of Electronics Industry, 2006: 88-89.
[16] Winkel J  . Modeling and simulating GNSS signal structures and receivers[D]. Munich: University FAF Munich. Faculty of Aerospace Engineering, 2000: 28-29.
. Modeling and simulating GNSS signal structures and receivers[D]. Munich: University FAF Munich. Faculty of Aerospace Engineering, 2000: 28-29.
(编辑 杨幼平)
收稿日期:2013-06-10;修回日期:2013-08-22
基金项目:教育部新世纪优秀人才支持计划项目(NCET-08-0144)
通信作者:王飞雪(1987-),男,福建长汀人,教授,从事卫星导航定位系统研究;电话:13607445251;E-mail:wangfeixue365@sina.com