J. Cent. South Univ. (2012) 19: 609-614
DOI: 10.1007/s11771-012-1046-x
Numerical simulation of particle deposition in obstructive human airways
OU Cui-yun(欧翠云), DENG Qi-hong(邓启红), LIU Wei-wei(刘蔚巍)
School of Energy Science and Engineering, Central South University, Changsha 410083, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: To investigate airflow pattern and its impact on particle deposition, finite-volume based computational fluid dynamics (CFD) simulations were conducted in the diseased triple-bifurcation airways. Computations were carried out for twenty Reynolds numbers ranging from 100 to 2 000 in the step of 100. Particles in the size range of 1-10 μm were conducted. Two particle deposition mechanisms (gravitational sedimentation and inertial impaction) were considered. The results indicate that there are strong relationship between airflow structures and particle deposition patterns. Deposition efficiency is different for different particles in the whole range of the respiratory rates. Particles in different sizes can deposit at different sites. Smaller particles can be uniformly deposited at the inside wall of the considered model. Larger particles can be mainly deposited in the proximal bifurcations. Deposition fraction varies a lot for different inlet Reynolds numbers. For lower Reynolds numbers, deposition fraction is relatively small and varies a little with varying the diameters. For higher Reynolds numbers,there is a most efficient diameter for each Reynolds number to target the aerosols at the specific site.
Key words: diseased airway; inhalable particle; airflow pattern; particle deposition
1 Introduction
The inhalation of allergens and toxic particles may be the cause of some local lung diseases, such as asthma, chronic obstructive pulmonary disease (COPD) and lung cancer. Considerable progress has been made in understanding the mechanisms of asthma as an inflammatory disease, but COPD has been relatively overlooked [1-2], while it is the fourth common cause of death and is predicted to catch up with lower respiratory tract diseases to become the third in the near future [3]. Structurally, both COPD and asthma are characterized by airflow obstruction and persistent inflammatory process.
The treatment of those lung diseases is often reliant on aerosolized drugs delivering into the airways through the inhalers [4]. Current inhaler devices have been designed to deliver aerosol drugs to the airways in patients with asthma, but not with COPD, which primarily affects the peripheral airways and lung parenchyma. The current drug delivery is not efficient, even for asthma, only 10%-20% of the inhaled drugs can be effective, and the extra drug load may cause side effects [5]. So, it is of importance to understand the particle transport and deposition in diseased human lungs.
There have been many ways to study the particle deposition in diseased airways, such as experimental method, and numerical method. It was concluded by some earliest experimental works that flow patterns were most likely dependent on the airway geometry. And in vivo experiment studied by CHALUPA et al [6] showed that patients with asthma produced different deposition patterns. Simulation of particle deposition in the diseased airways can give suggestions about the assessment of adverse health effects of inhaled particles and optimization of the aerosol drug delivery.
Numerical method has been widely used to investigate particle deposition in the diseased human lungs. YANG et al [7] showed that single or double bifurcation airway may not be enough to accurately simulate the flow within human lung airways. Thus, YANG et al [8] studied the respiratory flow behavior in triple bifurcation COPD airways (G5-G8). LUO et al [9] investigated the particle deposition in narrowing airways, suggesting that particle deposition is influenced by the obstructions. ZHANG et al [10] and KLEINSTREUER and ZHANG [11-12] studied the particle transport and deposition in a triple bifurcation bronchial airway model with local tumors, indicating that particle deposition on the tumor surface may be impacted by the local occlusion, such as the tumor location and tumor size. FARKAS and BAL?SH?ZY [13] simulated the effect of local obstruction and blockage on airflow and aerosol deposition in central human airways (G3-G5). They also revealed that the particle deposition patterns may be significantly changed by airway disorders.
All above simulation studies demonstrated that numerical method can be a potential tool to investigate the aerosol deposition in the diseased airways, but there is still much work to be done. This work is mainly on the airflow and particle deposition in a triple bifurcation diseased airway model, with one branch constricted。g way d lung ause side effects patterns for icle deposition patterns under the considered mechanisms, 3-D views of particle de.
2 Method
2.1 Airway geometry
The human tracheobronchial tree consists of a system of dichotomous tubular bifurcations. This means that the basic unit of airway model is a bronchial bifurcation, which generally consists of one parent branch, two daughter branches and a divider between them. The bifurcation structure has a strong relation with both the airflow pattern and inhalable aerosol deposition in the human lung airways. Although the symmetric Weibel Type A (1963) [14] airway configuration is not fully realistic, its 3D bifurcating geometries can be expected to generate accurate local deposition calculations. The first step of this work is to generate a 3D triple bifurcation geometry, which is derived from the 3rd to 6th generation of the Weibel (1963) model only with one of the 5th generation branches constricted by 25% in the middle of the branch (G5.2 in Fig. 1). For this purpose, the UNIGRAPHICS (UG5.0) and GAMBIT pre-processing tools are used, taking into account the exact mathematical description of the morphologically realistic bifurcation model of HEGED?S et al [15]. Then, a 3D symmetric triple bifurcation airway model is achieved, as shown in Fig. 1, which also depicts the generation parameters. The dimensions are similar to those given by Weibel for adults with a lung volume of 3 500 mL.
2.2 Governing equations
Airflow was assumed to remain laminar throughout the flow field so that no turbulent modeling was employed. Thus, for the 3D incompressible steady laminar flow in rigid airways, the Navier-Stokes equations are given as follows:
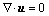 (1)
(1)
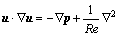 (2)
(2)
where u=(u, v, w) is the velocity vector, p is the pressure. All these variables are dimensionless and defined with the dimensional variables by x=x/D3, u=u/U, p=p/ρU2, where x=(x, y, z) is the Cartesian position vector, U is the mean velocity at the inlet cross-section and varies with the breathing rate, and ρ is the air density, 1.225 kg/m3. The Reynolds number is defined as Re=ρUD3/μ, and air dynamic viscosity μ=1.789 4×10-6 kg/(m·s). Computations are carried out for Reynolds numbers ranging from 100 to 2 000, corresponding to the mean inlet velocity from 0.26 to 5.2 m/s.
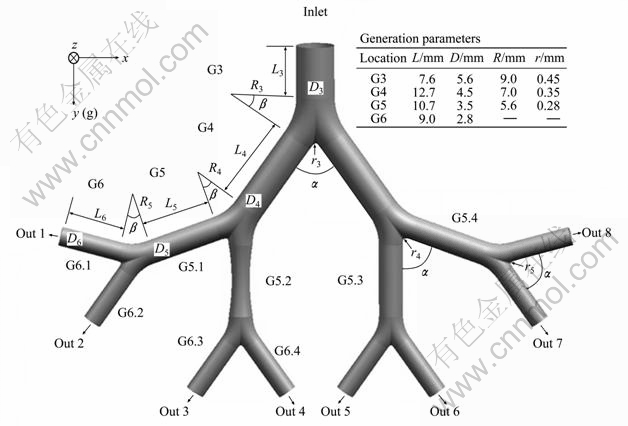
Fig. 1 Physical model of triple bifurcation unit of obstructive human lung airways (G3-G6)
For the steady state flow, spherical particle trajectories were determined by post-processing which is also called the one-way coupled method. In the size range above, 1 μm particles are deposited mainly due to the inertial impaction and gravitational sedimentation mechanisms. Thus, the drag and gravity are considered to be the dominant particle forces; then, the trajectory equation can be written as
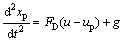 (3)
(3)
where xp is the particle displacement, up is the particle velocity, and g is the gravitational acceleration.
And FD(u-up) represents the drag force per unit particle mass given by
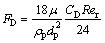 (4)
(4)
where ρp is the density of particle, dp is the particle diameter, and the relative Reynolds number Rer is defined as
 (5)
(5)
For the drag coefficient, there is
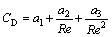 (6)
(6)
where a1, a2 and a3, applied for spherical particles, are constants for the certain size particles [16-17].
2.3 Numerical method
A structured, multi-block, body-fitted coordinate discretization scheme is used for the numerical program. The nonlinear convection terms in the Navier-Stokes equation are discretized by using the QUICK scheme to ensure an upwind character and high order accuracy. A segregated implicit approach is used to obtain the steady solution to ensure a fast convergence and a low memory requirement. The standard scheme is used to discretize the pressure gradients. The velocity fields are obtained by solving the momentum equations using an intermediate pressure field, which in turn are corrected through the computed velocity and the continuity equation using the SIMPLE algorithm. And relaxation factors for the velocity and pressure are chosen to be 0.7 and 0.3, respectively.
2.4 Deposition parameters
The regional deposition of micron particles in human airways can be quantified in terms of the deposition efficiency (ED) and deposition fraction (FD) in a specific region, and they are defined as
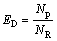 (7)
(7)
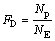 (8)
(8)
where Np is the number of deposited particles in a specific region; NR is the number of particles entering this region; NE is the number of particles entering the entire model.
2.5 Model validation
A validation study of bifurcation deposition efficiency for a range of particle sizes has been executed by comparing our numerical results with the computed data of COMER et al [18] and experimental data of KIM and FISHER [19]. As Fig. 2 shows, our simulation results are very close to both of the previous computational and experimental data, although there is little overestimation for deposition efficiency of the first bifurcation. These small discrepancies can be attributed to the wider range of experimental Reynolds numbers (472≤Re≤2 831) beyond the laminar flow regime considered in the numerical method, experimental indeterminacy and small differences between the numerical geometry and experimental glass tube models.
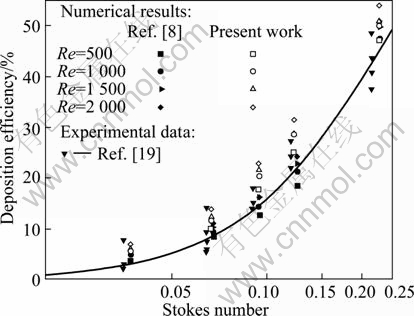
Fig. 2 Comparisons between present work and other works for double bifurcation
3 Results and discussion
3.1Airflow structures
Figure 3 shows the axial contours and secondary velocity vector distributions in different cross sectional slices of the constricted branch (G5.2) for the cases of Re=500 and Re=1 000. It can be seen that the airflow patterns, including the axial and secondary velocity profiles, vary a lot from the beginning of the specific branch to the end. The air stream is constricted firstly to the middle of the branch, and then expands to the end. When the upstream asymmetric air passes through the first part of the branch, its axial velocity becomes stronger, and its secondary velocity becomes weaker. While the air passes through the rest part, its axial velocity lowers down, and the secondary velocity keeps on decreasing. By comparing Fig. 3(a) with (b), similar tendency can be found in the two cases, only different in the strength of both axial and secondary velocities.
Fig. 3 Secondary velocity distributions in different sections of branch G5.2: (a) Re=500; (b) Re=1 000
3.2 Particle deposition patterns
Figure 4 shows ED of particle at different Reynolds numbers in the range of 1≤dp≤10 μm. Generally, the particle deposition efficiency increases with its diameter, because the dominating mechanisms are particle diameter dependent. Considering the influence of Reynolds numbers, the difference of deposition efficiency among the illustrating Reynolds numbers is large. When Re=100, the particle deposition efficiency increases gradually in the particle diameter range of 1-10 μm. When Re≥500, the curves of deposition efficiency for particles smaller than 2 μm are almost overlapped near the horizontal ordinate, while for particles larger than 3 μm, the values increase rapidly with Reynolds number. In order to find out the reason for those differences, deposition efficiencies have been studied for particles at different sizes due to different deposition mechanisms.
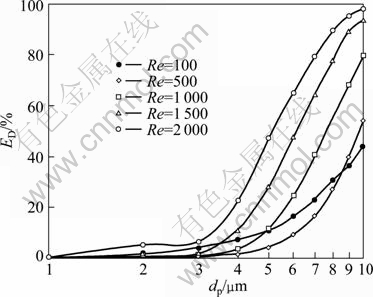
Fig. 4 Particle deposition efficiency at different Reynolds numbers
In order to describe qualitatively the local particle deposition patterns under the considered mechanisms, 3D views of particle deposition patterns are introduced. Figure 5 depicts the 5 μm and 10 μm particle deposition patterns for the cases of Re=100 and Re=2 000. As shown in Fig. 5, particles deposit symmetrically at the first bifurcation due to its symmetric geometry. However, asymmetric particle depositions in the second carina are clearly seen for all the Re ranges and particle diameters. For Re=100, particles distribute uniformly at the inside wall of tubes, and no dominant deposition site is found for particles in both diameters. Particles can deposit on the upper surface of the constricted branch (G5.2) because of the airflow redistribution, while on the contrary, no deposition can be seen on branch G5.3 because at low Reynolds number particles can only deposit at the sites perpendicular to the gravity direction. So, particles deposit more at the lateral tubes (G5.1 and G5.4) than at the medial tubes (G5.2 and G5.3). For Re=2 000, significant hot spots can be found at carina due to the relatively higher flow rate, making it more difficult for particles to follow the air streams. When considering the deposition at the third generation, it is found that more and more particles deposit at the inside wall of the medial tubes due to the enhanced inward secondary flows and inertial impaction. In the obstructed tube (G5.2), particles mainly deposit at the upper part where air stream is constricted. Nearly no particle deposits at the lateral branches of the fourth generation, as the airstream is highly redistributed among branches of this generation.

Fig. 5 Particle deposition patterns: (a) Re=100, dp=5 μm; (b) Re=100, dp=10 μm; (c) Re=2 000, dp=5 μm; (d) Re=2 000, dp=10 μm
In order to investigate the diameter range in which the particle can deposit most at the diseased site and to assess the corresponding health effects, particle deposition fraction at the specific site was introduced. Figure 6 depicts 1-10 μm deposition fraction (FD) at the constricted tube under five different Reynolds numbers. As shown in Fig. 6, we can see that for particles smaller than 2 μm, the deposition fraction is nearly zero. When particles are bigger than 2 μm, their deposition fraction is different for different Reynolds numbers. When Re≤500, deposition fraction is relatively small, and varies a little with the varying diameters, which indicates that it is not propitious for aerosol drug delivery at low respiratory rates; on the contrary, it is helpful for patients to reduce the exposure risk over the aerosol pollutants. For higher Reynolds numbers, e.g. Re=1 000, the deposition fraction increases with increasing the particle diameter, which indicates that the bigger the particle is, the better it targets at the specific site. When Re is increased, particle deposition fraction first increases rapidly with Re, and then rapidly decreases with Re. Thus, there is a most efficient diameter for each Reynolds number to target the aerosols at the specific site.
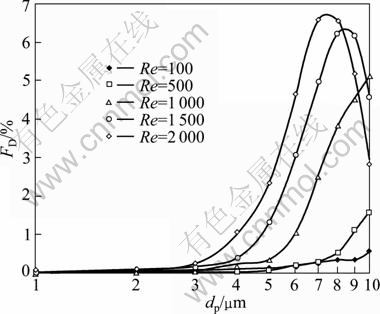
Fig. 6 Particle deposition fraction at specific sites under different inlet Reynolds numbers
4 Conclusions
1) Airflow structures, including axial velocity and secondary velocity, which can influence the particle deposition patterns, are greatly impacted by the airway disorders.
2) Particle deposition efficiency increases with the particle diameter, because the dominating mechanisms are particle diameter dependent. Reynolds numbers can influence the particle deposition pattern, i.e. the difference of deposition efficiency among the illustrating Reynolds numbers is large.
3) Smaller particles can be uniformly deposited at the inside wall of the considered model. Larger particles can be mainly deposited in the proximal bifurcations, and significant hot spots can be found in the vicinity of the first carina.
4) Deposition fraction varies a lot for different inlet Reynolds numbers. For lower Reynolds numbers, deposition fraction is relatively small, and varies a little with varying the particle diameters. For higher Reynolds numbers,there is a most efficient diameter for each Reynolds number to target the aerosols at the specific site.
References
[1] BARNES P J, CELLI B R. Systemic manifestations and comorbidities of COPD [J]. European Respiratory Journal, 2009, 33: 1165-1185.
[2] BARNES P J. Immunology of asthma and chronic obstructive pulmonary disease [J]. Nature Reviews Immunology, 2008, 8: 183-192.
[3] KLEINERT S. COPD—Call for papers [J]. The Lancet, 2009, 373: 108.
[4] JAWOREK A. Micro- and nano-particle production by electrospraying [J]. Powder Technology, 2007, 176 (1): 18-35.
[5] WELTE T. Optimising treatment for COPD–New strategies for combination therapy [J]. The International Journal of Clinical Practice, 2009, 63(8): 1136-1149.
[6] CHALUPA D C, MORROW P E, OBERD?RSTER G, UTELL M J, FRAMPTON M W. Ultra?ne particle deposition in subjects with asthma [J]. Environmental Health Perspectives, 2004, 112: 879-882.
[7] YANG X L, LIU Y, SO R M C, YANG J M. The effect of inlet velocity profile on the bifurcation COPD airway flow [J]. Computers in Biology and Medicine, 2006, 36: 181-194.
[8] YANG X L, LIU Y, LUO H Y. Respiratory flow in obstructed airways [J]. Journal of Biomechanics, 2006, 39: 2743-2751.
[9] LUO H Y, LIU Y, YANG X L. Particle deposition in obstructed airways [J]. Journal of Biomechanics, 2007, 40: 3096-3104.
[10] ZHANG Z, KLEINSTREUER C, KIM C S, HICKEY A J. Aerosol transport and deposition in a triple bifurcation bronchial airway model with local tumors [J]. Inhalation Toxicology, 2002, 14: 1111-1133.
[11] KLEINSTREUER C, ZHANG Z. Targeted drug aerosol deposition analysis for a four-generation lung airway model with hemispherical tumors [J]. Journal of Biomechanical Engineering, 2003, 125: 197-206.
[12] KLEINSTREUER C, ZHANG Z. An adjustable triple-bifurcation unit model for air-particle flow simulations in human tracheobronchial airways [J]. Journal of Biomechanical Engineering, 2009, 131(2):
[13] FARKAS ?, BAL?SH?ZY I. Simulation of the effect of local obstructions and blockage on airflow and aerosol deposition in central human airways [J]. Journal of Aerosol Science, 2007, 38: 865-884.
[14] WEIBEL E R. Morphometry of the human lung [M]. New York: Springer, 1963: 140-151.
[15] HEGED?S C J, BAL?SH?ZY I, FARKAS ?. Detailed mathematical description of the geometry of airway bifurcations [J]. Respiratory Physiology & Neurobiology, 2004, 141: 99-114.
[16] MICHAELIDES E E. Particles bubbles and drops: Their motion, heat and mass transfer [M]. World Scientific Publishing Co Pte Ltd, 2006: 165-175.
[17] MORSI S A, ALEXANDER A J. An investigation of particle trajectories in two-phase flow systems [J]. Journal of Fluid Mechanism, 1972, 55: 193-208.
[18] COMER J K, KLEINSTREUER C, HYUN S, KIM C S. Aerosol transport and deposition in sequentially bifurcating airways [J]. Journal of Biomechanical Engineering, 2000, 122: 152-158.
[19] KIM C S, FISHER D M. Deposition characteristics of aerosol particles in sequentially bifurcating airway models [J]. Aerosol Science and Technology, 1999, 31: 198-220.
(Edited by YANG Bing)
Foundation item: Project(51178466) supported by the National Natural Science Foundation of China; Project(200545) supported by the Foundation for the Author of National Excellent Doctoral Dissertation of China; Project(2011JQ006) supported by the Fundamental Research Funds of the Central Universities of China
Received date: 2011-07-26; Accepted date: 2011-11-14
Corresponding author: DENG Qi-hong, Professor, PhD; Tel: +86-731-88877175; E-mail: qhdeng@csu.edu.cn