DOI： 10.11817/j.issn.1672-7207.2021.02.015
TM耦合下科钻深井结晶岩井壁失稳力学响应规律
王李昌1, 2，朱自强1, 2，雷家蔚3，张绍和1, 2，隆威1, 2，舒彪1, 2
(1. 中南大学 地球科学与信息物理学院，湖南 长沙，410083；
2. 有色金属成矿预测与地质环境监测教育部重点实验室，湖南 长沙，410083；
3. 中铁二院工程集团有限责任公司，四川 成都，610031)
摘要：依据热力(thermo-mechano，TM)耦合影响下坍塌和破裂压力计算模型，探讨8 000 m科钻深井处结晶岩井壁失稳规律。在温度为260 ℃、应力为200 MPa时，采用Mohr-Coulomb破坏准则和最大拉应力理论，通过力学推导和MATLAB编程运算求解坍塌、破裂压力演化模型；揭示TM耦合下井壁失稳的力学响应规律，得出钻井液安全密度窗口，以便为井眼轨迹设计和钻井液优选提供指导。研究结果表明：当井眼轨迹沿最大或最小水平地应力方向钻井时，井壁在最小水平地应力方向最易坍塌，在最大水平地应力方向最易破裂；坍塌、破裂压力在一定深度的井壁上呈周期性规律分布，最易破坏点随着井斜角、方位角的变化而变化；热效应对井壁破裂压力的影响明显，钻井液循环改变了安全密度窗口大小；钻井液安全密度窗口可为井眼轨迹设计和钻井液优选提供指导。
关键词：结晶岩；热力耦合；坍塌压力；破裂压力；安全密度窗口
中图分类号：P642.3 文献标志码：A
文章编号：1672-7207（2021）02-0465-13
Mechanical responses to wellbore instability of crystalline rocks in scientific deep well during thermo-mechano coupling
WANG Lichang1, 2, ZHU Ziqiang1, 2, LEI Jiawei3, ZHANG Shaohe1, 2, LONG Wei1, 2, SHU Biao1, 2
(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring, Ministry of Education, Central South University, Changsha 410083, China;
3. China Railway Eryuan Engineering Graup. Co. Ltd., Chengdu, Sichuan 610031, China)
Abstract: Based on the model calculation of the collapse and fracture pressure under the thermo-mechano coupling, the wellbore instability of crystalline rock in a scientific depth of 8 000 m was discussed. At 260 ℃ and 200 MPa, the evolution models of collapse and fracture pressure were developed by mechanical calculations on MATLAB based on Mohr-Coulomb failure criterion and the maximum tensile stress theory. The mechanical responses to the wellbore instability of crystalline rock formation during the thermo-mechano coupling were revealed, and the safety density window of drilling fluid was obtained. These would provide guidance for the well structure design and drilling fluid optimization for the scientific deep wells. The results show that, when the wellbore is drilled along the direction of the maximum or the minimum horizontal ground stress, wellbore inclines to collapse and fracture in the minimum and the maximum horizontal ground stress directions, respectively. The collapse and fracture pressures are periodically distributed on the wellbore with depth, and the most vulnerable points change with the azimuth and oblique angles. The thermal effect is significant under the wellbore fracture pressure, and the drilling fluid circulation changes the safety density window size in the scientific deep well. The safety density window of drilling fluid can provide guidance for the well structure design and drilling fluid optimization for the scientific deep wells.
Key words: crystalline rock; thermo-mechano coupling; collapse pressure; fracture pressure; safety density window size
科学钻探深井是为研究地球内部活动获取直接资料而进行的钻探工程，是开展深部地质调查与探测的关键科学性技术手段[1]。张金昌等[2]提出实施13 000 m科钻特深井的技术方案，指出6 000~ 7 000 m以下为结晶岩层，其主要特点是存在破碎带、弱强度地层和强致斜岩石，井底温度在250 ℃以上，井壁失稳问题突出[2]。结晶岩是一种由多成分构成具有多晶复合介质特点的脆性坚硬岩石，非均质性强，内部存在原生微裂纹、矿物解理、晶粒和晶界等，也存在流动结构早期塑性变形或脆性断裂[3]。受高温地应力(即热力耦合，thermo-mechano，TM)作用[4-5]，深部结晶岩流变特性明显，井眼打开后出现能量释放应力重平衡与热扩散传导过程，伴随着井壁变形与围岩流变，甚至出现坍塌、破裂、缩径、掉块及岩心碎片化等现象，引发卡钻埋钻等事故[6]。TM耦合作用下结晶岩流变主要是由于原生结构、微裂纹及新裂纹扩展变化，也就是产生热破裂和应力损伤破裂复合破裂过程，宏观上表现为蠕变、膨胀及扩容[7]，进而可能导致深井井壁失稳。由此可知，井壁失稳是TM耦合作用下井眼轨迹、岩石特性、弱结构面、裂缝等多因素影响的复杂变化过程[8]，其中热效应对井壁破裂、坍塌压力影响明显，是井壁失稳破裂破坏的主要原因[9-10]。对井壁围岩应力状态与岩石破坏准则进行平衡分析是判断井壁是否稳定的核心[11]。深部钻井是一种应力重平衡的过程，当应力分布处于欠平衡状态时，井壁失稳，其主要表现形式有坍塌、缩径和破裂，力学机理主要是剪切破坏和拉伸破裂，可通过坍塌与破裂压力变化来定量评价井壁失稳状态和力学响应演化规律[12]。本文以8 000 m科钻深井为研究对象，考虑在温度为260 ℃和应力为200 MPa作用下，采用Mohr-Coulomb破坏准则和最大拉应力理论[13]，依据热弹性理论，通过力学推导和MATLAB编程运算求解[14]，研究温度、井眼轨迹变化下的井壁坍塌、破裂压力变化规律，得出钻井液安全密度窗口，以便揭示TM耦合下科钻深井结晶岩井壁失稳的力学响应演化规律。
1 深井井壁稳定力学原理及岩石破坏准则
深井井筒受力及力学分解模型见图1。井壁稳定受地应力、温度、孔隙压力、液柱压力、岩石特性等多个因素影响，其平衡状态力学分析模型的构建十分关键[15](图1(a))。钻井中地层原有平衡被打破，液柱压力取代了岩心的平衡应力，井周应力重新分布寻求新平衡。当井壁应力超过其强度包络线时，井壁发生破坏。不同井眼轨迹的井壁应力状态不同，本文以直井与定向井(斜井+水平井)为研究对象，假设地层是均匀各向同性、线弹性多孔材料，并认为井周岩石处于平面应变状态。
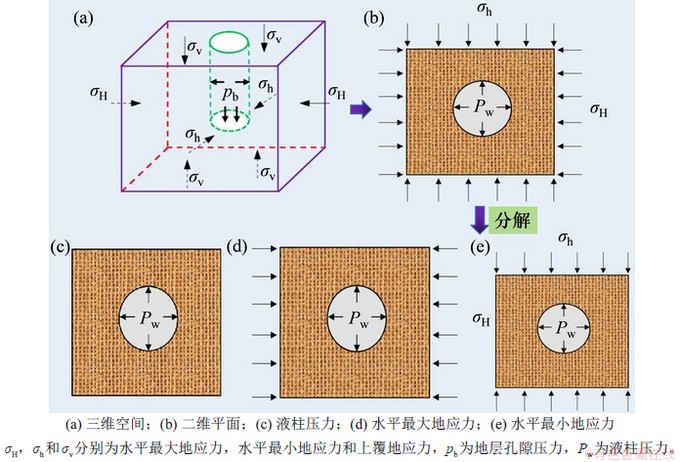
图1 深井井筒受力及力学分解模型
Fig.1 Wellbore stress and mechanical decomposition models of scientific deep wells
1.1 直井井壁稳定力学模型
在无限大平面上，1个圆孔承受均匀内压，在无限远处有2个水平地应力同时作用[16]，其垂直方向有上覆地应力。考虑岩石为小变形弹性体，故线性叠加原理适用。井周的总应力状态可通过各应力分量对井周的应力贡献总和求得。井壁受力力学模型分解如图1(b)，(c)，(d)和(e)所示。结合分解模型在柱坐标系中的应力表达式[17]，求解出地应力作用下，考虑液柱压力的井周地层应力分布：
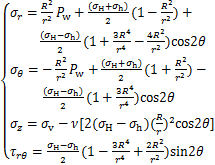(1)
式中：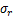
为井壁径向应力；
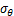为井壁周向应力(切向应力)；
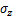为井壁轴向应力；
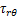为剪切应力；ν为地层泊松比；σH，σh和σv分别为水平最大地应力、水平最小地应力和上覆地应力；Pw为液柱压力；R和r分别为井眼半径和井眼轴线到地层中某点的矢径；θ为井周角。
1.2 定向井井壁稳定力学模型
定向井井周应力分布不仅受地应力等影响，还与井斜角、方位角等井眼轨迹参数密切相关，通常在柱坐标系内进行分析，因此，需对地应力向柱坐标系进行变换。选取坐标系(1，2，3)分别与主地应力σH，σh和σv方向一致，如图2所示。
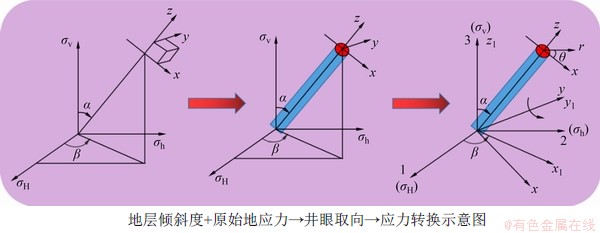
图2 定向井坐标系与应力转换
Fig. 2 Diagram of directional wellbore coordinate system and stress transformation
建立直角坐标系(x，y，z)和柱坐标系(r，θ，z)，其中Oz轴对应于井轴，Ox轴和Oy轴位于与井轴(柱)垂直的平面之中。如图2所示，应力转换与坐标旋转过程如下：先将坐标(1，2，3)以3为轴，按右手定则旋转角β，变为(x1，y1，z1)坐标；(x1，y1，z1)以y1为轴，按右手定则旋转角α，变为(x，y，z)坐标。其中，β为井斜方位与水平最大地应力方位的夹角，α为井斜角。经推导可得各应力分量：
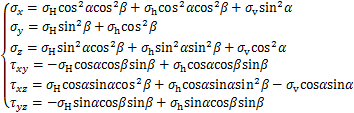(2)
完成应力变换后，利用包括平衡方程、协调方程、本构关系和边界条件的弹性力学基本方程，推导井周应力分布。在地应力作用下，考虑液柱压力的井周应力分布状态方程为[18]
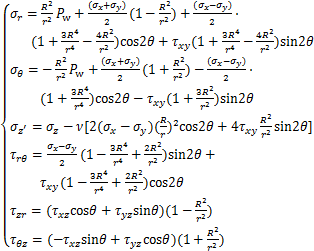(3)
1.3 热效应下井壁稳定力学模型
科学深井的应力集中高温热效应不仅对钻具等材料的性能产生影响，更会对结晶岩产生影响并引起井壁失稳[19]。液柱压力和井壁温度变化易改变井周应力和温度分布，由温变引起的附加应力会导致井壁坍塌、破裂。热效应对井壁稳定影响明显[20-21]，其作用是以围岩的膨胀或收缩等热应变形式表现出来。忽略温度变化对地层流变参数的影响，不计入地层流体和岩石骨架变形过程中的耦合作用，依据孔隙热弹性理论，考虑热效应下井周附加应力场，求解出TM耦合作用下的定向井井周应力分布：
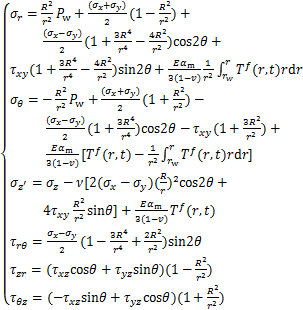(4)
式中：αm为岩石热膨胀系数；σrT，σθT和σzT分别为温变引起的井壁附加径向、周向和轴向应力；Tf(r，t)=T(r，t)-T0为井周围岩热效应场。其中，Tf(r，t)为井周围岩温度变化；T(r，t)为井周围岩温度；T0为地层初始温度，结合井壁应力分布状态，将剪应力转换为主应力进行计算，并减去岩石中相应承受的孔隙压力，通过求解得井壁有效应力：
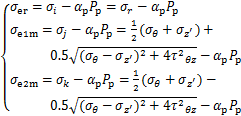(5)
式中：αp为有效应力系数；Pp为孔隙压力。在井壁稳定性研究中，令σ1=max(σer，σe1m，σe2m)，σ3=min(σer，σe1m，σe2m)，其中，σ1为最大主应力；σ3为最小主应力；σer，σe1m和σe2m为主应力分量。
2 MATLAB求解方法
将定向井中地应力转换为主应力并确定其值的求解过程复杂，同时将主应力代入破坏准则求解坍塌、破裂压力时需采用迭代法，还需筛选出不同井周角处初始破坏点对应的坍塌、破裂压力。针对该复杂过程，为此，选取MATLAB为运算平台，开展编程模拟计算求解(见图3)，具体流程如下：1) 输入参数σH，σh，σv，Pp，E，C，φ，ν，St，αp，αm，α，β和ΔT；2) 确定计算的基础参数，代入式(3)和(4)求解出TM耦合下井壁稳定力学模型的井壁应力分布；3) 取θ=0°~360°，按精度要求划分计算步距，根据式(5)计算并筛选出不同参数下各井周角的σ1和σ3；4) 基于式(6)和(7)，求解出坍塌压力ρT、破裂压力ρp在不同井周角处变化规律；5) 筛选出井斜角、方位角、温度变化下的最大坍塌压力(ρT)max和最小破裂压力(ρp)min位置，得出随井眼轨迹的变化规律和井壁温度变化对钻井液密度窗口的影响规律。
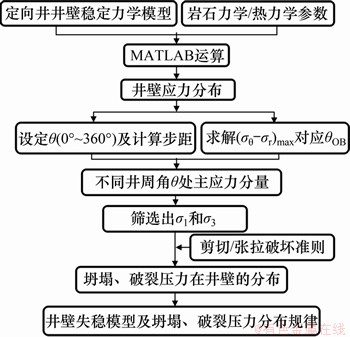
图3 MATLAB求解井壁失稳规律流程
Fig. 3 Flow of mechanical responses for wellbore instability obtained by MATLAB
3 定向井井壁失稳力学响应规律
基于针对σH>σv>σh的原地应力状态实例研究失稳力学响应规律[22]。根据CCSD-1、松科2井及已有资料，选取科学井深H=8 000 m处结晶岩井壁，垂直地应力梯度为0.025 MPa/m，垂直、最大和最小地应力梯度差为0.002 MPa/m，地层初始温度为260 ℃，上覆地应力σv=200 MPa，水平最大地应力σH=216 MPa，水平最小地应力σh=184 MPa，地层弹性模量E=53 GPa，地层孔隙压力Pp=84 MPa，岩石黏聚力C=15 MPa，岩石抗拉强度St=2.1 MPa，地层有效应力系数αp=0.9，泊松比ν=0.39，岩石内摩擦角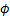
=53.9°，岩石热膨胀系数αm=3.5×10-5，井壁温度变化ΔT1=20 ℃和ΔT2=-20 ℃，以钻井液当量密度表征坍塌、破裂压力。
3.1 坍塌失稳力学响应规律
针对定向井井壁坍塌失稳状态可用坍塌压力进行定量评价，其力学机理是井壁岩石发生压剪破坏，其原因是液柱压力较低，围岩所受应力超过岩石本身强度。本文选用Mohr-Coulomb准则，井壁岩石发生剪切破坏可表示为
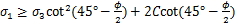(6)
式中：σ1=max(σer，σe1m，σe2m)，σ3=min(σer，σe1m，σe2m)。
3.1.1 坍塌压力在井壁的分布规律
在深井热交换传导效应下，当井眼方位角β为0°，30°，60°和90°时，不同井斜角(α为30°和60°)和井壁温度变化(ΔT为20 ℃和-20℃)下坍塌压力随井周角的变化规律如图4所示。从图4可见：坍塌压力在井壁全井周角呈周期性规律化分布，最大坍塌压力随温度升高或井斜角减小而增大，因此，温度升高和井斜角减小增强了井壁剪切破坏能力，需提高液柱压力来平衡井壁稳定。从图4(a)可见：当深井钻井方向与水平最大地应力方向平行(β=0°)时，井壁最小坍塌压力点在井周角θ=0°和θ=180°处，最大坍塌压力点在θ=90°和θ=270°处，因此，当钻井液密度小于某个临界值时，井壁将在水平最小地应力方向上最早发生剪切破坏。从图4(b)和图4(c)可见：当方位角β为30°和60°时，井壁最大、最小坍塌压力点的井周角随井斜角的变化而变化，井壁最易发生坍塌的位置也随之变化；随着井斜角增大，最大坍塌压力逐渐减小，最小坍塌压力逐渐增大。由图4(d)可知：当井眼轨迹轴线沿水平最小地应力方向倾斜时，最大、最小坍塌压力所处井壁位置的井周角与方位角β=0°时(图4(a))一样并不随井斜角的变化而变化；但随着方位角β由0°转至90°时，最大坍塌压力所对应的井周角θ由90°和270°分别偏移至0°和180°。可见，沿水平最小地应力方向钻井的井壁最易坍塌位置也指示为水平最小地应力方向，与井眼沿水平最大地应力方向钻井时的最易坍塌位置一致。
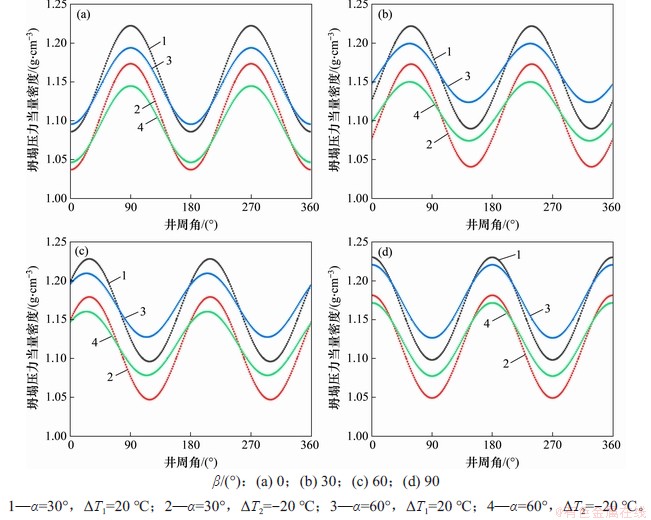
图4 热效应下坍塌压力随井周角、井斜角变化规律
Fig. 4 Collapse pressure change with wellbore round and oblique angles under thermal effect
在深井热交换传导效应下，当井眼井斜角α为30°和60°，不同方位角(β为0°，30°，60°和90°)和井壁温度变化(ΔT为20 ℃和-20 ℃)作用下坍塌压力随井周角的变化规律如图5所示。从图5可见：坍塌压力随着井壁温度升高而增大，随着井周角增大而呈周期性规律变化；当井斜角不变时，在相同井周角处的坍塌压力随着方位角变化而变化，在全井周中井壁最易坍塌破坏点也随之变化；当方位角由沿水平最大地应力方向(β=0°)变化至水平最小地应力(β=90°)时，井壁最大坍塌压力所处井周角位置由θ=90°转移至θ=0°，由此可知沿水平最大和最小地应力方向钻井时，井壁岩石在水平最小地应力方向最易发生坍塌破坏。最大、最小坍塌压力随着方位角增加呈增大趋势，这一增大趋势随着井斜角增大更加明显，井斜角α=60°时的最小坍塌压力比α=30°时的最大坍塌压力增大趋势更加明显。
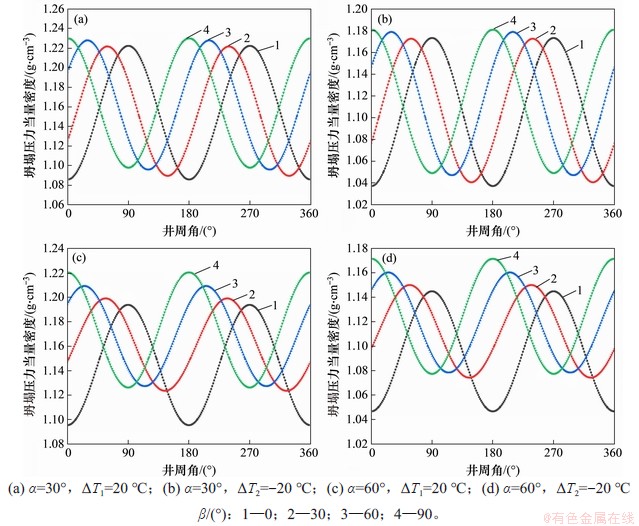
图5 热效应下坍塌压力随井周角、方位角变化规律
Fig.5 Collapse pressure change with wellbore round and azimuth angles under thermal effect
同一深井相同井斜角、方位角和深度处的井壁坍塌压力空间分布并不相同，随着井周角变化呈周期性规律化分布，最大与最小坍塌压力点是确定的，因此，在实际井身结构设计中，不仅要考虑井眼轨迹(井斜角、方位角、深度)对井壁坍塌的影响，更要考虑全井周角坍塌压力分布计算。随着钻井液循环井壁温度降低，坍塌压力减小，有利于井壁稳定。
3.1.2 坍塌压力随井眼轨迹的变化规律
图6所示为井壁温度升高ΔT1=20 ℃，不同方位角(β为0°，30°，45°，60°和90°)条件下坍塌压力随井斜角变化规律。从图6可见：坍塌压力随井斜角的增大而减小，表明斜井与直井(α=0°)相比，其井壁抗剪切破坏能力更强、更加稳定，坍塌压力减小的速率随着方位角的增大而减小；当井斜角α在0°~75°间变化时，沿水平最大地应力方向钻井的井壁坍塌压力最小，不易发生坍塌破坏；对于任意井斜角，沿水平最小地应力方向，钻井的坍塌压力最大，井壁稳定性最弱。对比沿水平最小主应力方向(β=90°)钻井的坍塌压力可知，沿水平最大主应力方向(β=0°)的坍塌压力随井斜角增大而降低的幅度更大，井壁更加稳定，同时，坍塌压力在方位角β=0°处比β=90°处小，说明沿水平最大地应力方向钻井要比沿水平最小地应力方向更加稳定、安全。井眼轨迹沿井斜角α=90°和β=30°钻井时的井壁坍塌压力最小，发生剪切破坏的可能性最小。
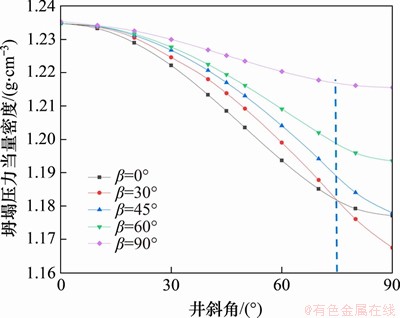
图6 坍塌压力随井斜角变化规律
Fig. 6 Collapse pressure change with oblique angle
图7所示为井壁温度升高ΔT1=20 ℃，不同井斜角(α为0°，30°，45°，60°和90°)条件下坍塌压力随方位角的变化规律如图7所示。从图7可见：井斜角α=0°时直井井壁坍塌压力基本上不随方位角变化而变化，其坍塌压力也最大，最易发生剪切破坏；当井斜角α为30°，45°和60°时，坍塌压力随方位角增加而增大；当井斜角α=90°时，坍塌压力随方位角的增加先减小后增大；当方位角β=30°且井斜角α=90°时，其井壁坍塌压力最小，稳定性最强。
3.2 破裂失稳力学响应规律
针对定向井井壁破裂失稳研究可用破裂压力进行定量评价。结合井壁岩石应力状态和力学特性，选用最大拉应力理论，分析井壁破裂压力[27]。井壁发生张拉破坏判别准则为
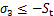(7)
式中：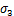
为最小主应力；
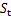为岩石抗拉强度。
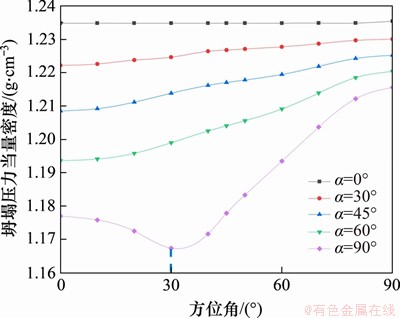
图7 坍塌压力随方位角变化规律
Fig. 7 Collapse pressure change with azimuth angle
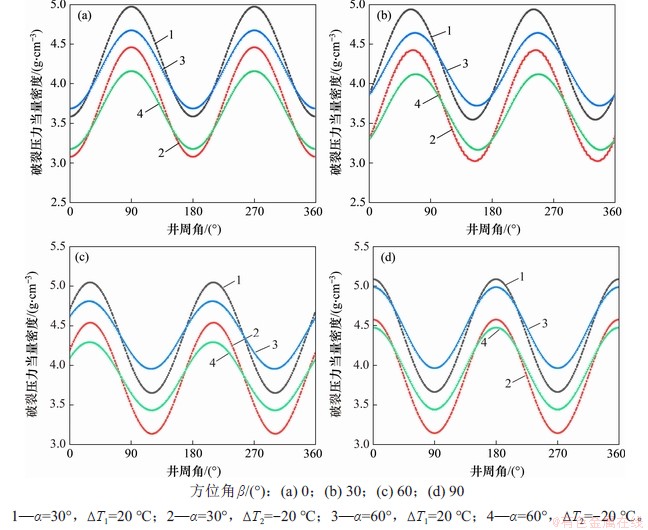
图8 热效应下破裂压力随井周角、井斜角的变化规律
Fig. 8 Fracture pressure change with wellbore round and oblique angles under thermal effect
3.2.1 破裂压力在井壁的分布规律
在深井热交换传导效应下，当井眼方位角β为0°，30°，60°和90°，不同井斜角(α为30°和60°)及井壁温度变化(ΔT为20 ℃和-20 ℃)时井壁破裂压力随井周角呈周期性规律化分布如图8所示。从图8可见：随着井斜角增加，最大破裂压力逐渐降低，最小破裂压力逐渐增大，破裂压力区间变小，相同深度处井壁抗拉伸破裂能力趋于一致；最大、最小破裂压力所处位置的井周角随着井斜角、方位角变化而变化；当β=0°时，最大破裂压力处于水平最小地应力方向(θ为90°和270°)，最小破裂压力处于水平最大地应力方向(θ为0°和180°)；当β=90°时，最大破裂压力处于水平最小地应力方向(θ为0°和180°)，最小破裂压力处于水平最大地应力方向(θ为90°和270°)。最小破裂压力处为井壁最易发生拉伸破坏位置，最大破裂压力处为井壁抗拉伸破坏能力最强位置。当井眼轨迹沿水平最大或最小地应力方向钻井时，最早发生破裂破坏的位置出现在最大地应力方向的可能性最大，在最小地应力方向的可能性最小。
在深井热交换传导效应下，当井眼井斜角α为30°和60°，不同方位角(β为0°，30°，60°和90°)和井壁温度变化(ΔT为20 ℃和-20 ℃)作用下井壁破裂压力随井周角呈周期性变化规律分布如图9所示。从图9可见：当钻井方向由沿水平最大地应力方向(β=0°)转至水平最小地应力(β=90°)时，最小破裂压力所处位置的井周角由θ=0°转至θ=90°，说明当沿水平最大和最小地应力方向钻井时，井壁在水平最大地应力方向最易发生破裂破坏；最大、最小破裂压力随着方位角增加呈增大趋势，这一增大趋势随着井斜角增大更加明显；井斜角α=60°时的最大、最小破裂压力比α=30°时的增大趋势更加明显。
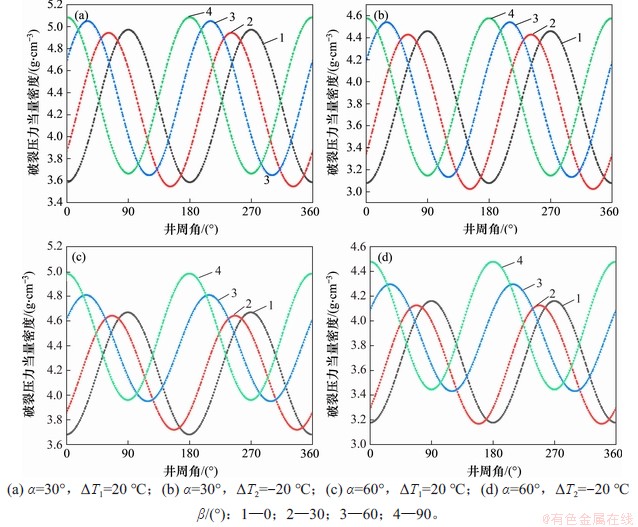
图9 热效应下破裂压力随井周角、方位角变化规律
Fig. 9 Fracture pressure change with wellbore round and azimuth angles under thermal effect
当井眼轨迹沿着水平最大或最小主应力方向钻井时，井壁最容易发生拉伸破裂破坏的位置处在水平最大地应力方向。当井眼轨迹方位逐渐偏移到水平最小地应力方向时，最大破裂压力略有增大。同一深井在相同井斜角、方位角和深度处的井壁破裂压力空间分布不同，随着井周角变化呈周期性规律化分布，最大与最小破裂压力点是确定的，因此，在实际井身结构设计中，不仅要考虑井眼轨迹(井斜角、方位角、深度)对井壁破裂的影响，而且要考虑全井周角破裂压力分布计算。同时，随着钻井液循环井壁温度降低，破裂压力随之减小，不利于井壁稳定。
3.2.2 破裂压力随井眼轨迹的变化规律
图10所示为井壁温度升高ΔT1=20 ℃，不同井眼方位角(β为0°，30°，45°，60°和90°)条件下，井壁破裂压力随井斜角变化规律。从图10可见：破裂压力随井斜角增大而增大，增大速率随方位角增大而增大，表明斜井相比于直井其井壁抗拉伸破坏能力更强，井壁更加稳定，破裂压力增大的速率在井斜角α=90°时趋于稳定；当井斜角α在0°~65°间变化时，沿水平最小地应力方向钻井的井壁破裂压力最大，其抗拉伸破坏能力最强，井壁不易发生破裂破坏；对于任意井斜角，破裂压力在方位角β=0°处比β=90°处小，说明沿水平最小地应力方向钻井的井壁发生破裂失稳的可能性比沿水平最大地应力方向的小；方位角β=60°且井斜角α=90°处的井壁破裂压力最大，井壁稳定性最强。
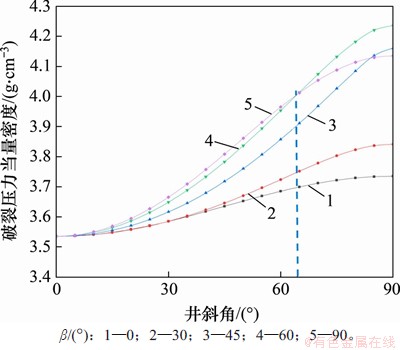
图10 破裂压力随井斜角变化规律
Fig. 10 Fracture pressure change with oblique angle
图11所示为井壁ΔT1=20 ℃，不同井斜角(α为0°，30°，45°，60°和90°)条件下，井壁破裂压力随方位角变化规律。从图11可见：当井斜角α=0°时，直井井壁破裂压力保持一个定值，不随方位角变化而变化；直井(α=0°)的井壁破裂压力最小，最易发生拉伸破坏；当井斜角α为30°，45°和60°时，破裂压力随方位角增加而增大；当井斜角α=90°时，破裂压力随方位角的增加先增大后减小。与直井对比，斜井及水平井的抗拉伸破坏能力更强。同时，井斜角α=90°且β=50°处的井壁破裂压力最大，地层承压能力更强，发生张拉破坏的可能性最小。
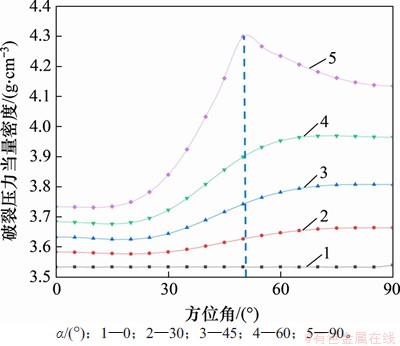
图11 破裂压力随方位角变化规律
Fig. 11 Fracture pressure change with azimuth angle
4 热效应对钻井液安全密度窗口的影响规律
基于上述科学深井参数开展热效应对结晶岩层钻井液安全密度窗口作用规律的研究，分析不同井眼轨迹深井井壁温度变化对钻井液安全密度的影响规律。图12为不同井眼方位角(β为0°，45°和90°)及井斜角(α为0°，45°和90°)条件下，钻井液安全密度窗口随温度降低幅度的变化规律。从图12可见：随着井壁温度降幅增大，坍塌、破裂压力当量密度逐渐降低，且破裂压力降低的速率要远大于坍塌压力降低的速率，安全密度窗口范围越来越小；对于任意方位角，随着井斜角增大，破裂压力随之增大的幅度要远大于坍塌压力随之减小的幅度；井斜角α=90°时安全密度窗口最大，钻井液配方的选择范围更广；在任意井壁温度降低条件下，坍塌压力随方位角几乎没有变化，井斜角α=0°的破裂压力随方位角的变化没有变化，为一固定值，但α为45°和90°时破裂压力随方位角的变化较大；同时，α=0°时的安全密度窗口最小，沿水平最大地应力方向(β=90°)和α=90°时钻井使用的钻井液安全密度窗口最大。
图13所示为不同井眼方位角(β为0°，45°和90°)及井斜角(α为0°，45°和90°)条件下，钻井液安全密度窗口随温度升高幅度的变化规律。从图13可见：随着井壁温度升高，坍塌、破裂压力当量密度逐渐增大，且破裂压力增大的幅度远大于坍塌压力的增大幅度，安全密度窗口变大；对于任意方位角，随着井斜角增大，破裂压力随之增大的幅度要远大于坍塌压力随之减小的幅度；井斜角α=90°时安全密度窗口最大；当井壁温度升高时，坍塌压力随方位角几乎没有变化，井斜角α=0°的破裂压力随方位角的变化也没有变化，为一固定值，但井斜角α为45°和90°时的破裂压力随方位角的变化而变化较大；同时，井斜角α=0°时的安全密度窗口最小，沿水平最大地应力(β=90°)方向和井斜角α=90°时钻井使用的钻井液安全密度窗口最大。由此可知，温度变化对破裂压力的影响更加显著，这是由于温度变化引起的热效应对地层弹性参数的影响较大。
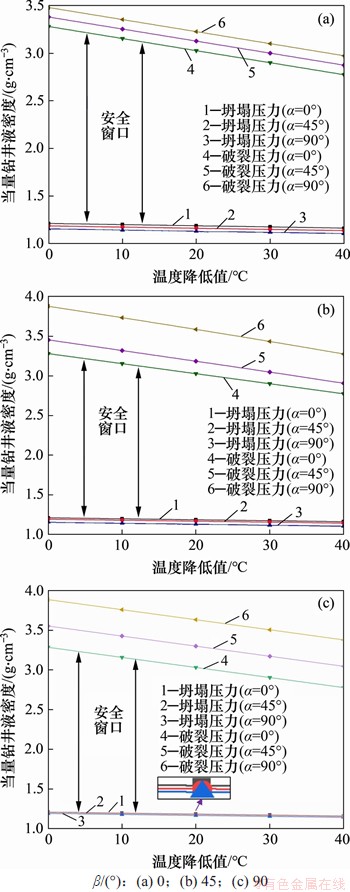
图12 坍塌、破裂压力当量密度随温度降幅的变化规律
Fig. 12 Equivalent density of collapse and fracture pressure change with decreasing temperature
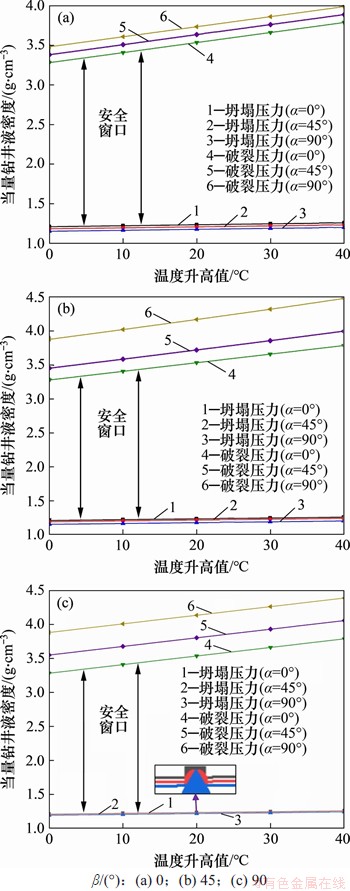
图13 坍塌、破裂压力当量密度随温度升高的变化规律
Fig. 13 Equivalent density of collapse and fracture pressure change with increasing temperature
5 结论
1) 当科学深井轨迹沿结晶岩地层最大或最小水平地应力方向钻井时，井壁在最小水平地应力方向最易坍塌以及在最大水平地应力方向最易破裂，当钻井液密度过低而引发井壁坍塌破坏时，初始坍塌位置能够指示最小水平地应力方向；当钻井液密度过高而发生井壁破裂破坏时，初始破裂位置能够指示最大水平地应力方向。
2) 当科学深井轨迹确定(井斜角、方位角和深度不变)时，坍塌、破裂压力在结晶岩井壁的空间分布呈周期性规律化分布，随着井周角变化而变化。当轨迹任一参数发生改变时，相同井周角处的坍塌、破裂压力随之改变，最易破坏点也发生变化。
3) 随井斜角增大，坍塌压力减小且减小速率变小，破裂压力增大且增大速率变大，表明斜井比直井的井壁抗剪切破坏和拉伸破坏能力更强，井壁更加稳定安全。
4) 直井(α=0°)的井壁坍塌压力最大、破裂压力最小且均不随方位角变化而变化，最易发生剪切和张拉破坏；当井斜角α为30°~60°时，坍塌、破裂压力均随方位角的增加而增大；当井斜角α=90°时，随方位角增加，坍塌压力先减小后增大，破裂压力先增大后减小。
5) 当温度升高ΔT=20 ℃时，方位角β=30°、井斜角α=90°的深井井壁坍塌压力最小，不易发生剪切破坏；方位角β=50°、井斜角α=90°的深井井壁破裂压力最大，抗拉伸破坏能力最强，发生破裂破坏的可能性最小。
6) 热效应对结晶岩井壁坍塌、破裂压力影响显著，尤其对破裂压力影响更加突出。坍塌、破裂压力随井壁温度降幅的增大而逐渐降低，且破裂压力降幅远大于坍塌压力的降幅，钻井液安全密度窗口变小，可选择配方范围变窄。坍塌、破裂压力随井壁温度升高而逐渐升高，且破裂压力升高幅度远比坍塌压力的大，钻井液安全密度窗口变大，可选择配方范围变宽。这说明在科学深井钻井液优选过程中，不仅要考虑初始安全密度窗口，更要考虑因钻井液循环引起热效应下作用下安全密度窗口的变化。
参考文献：
[1] 张培丰. 地层温度对科学超深井井壁稳定的影响[J]. 探矿工程(岩土钻掘工程), 2011, 38(10): 1-5.
ZHANG Peifeng. Effect of the formation temperature on the hole-wall stability in ultra-deep scientific drilling[J]. Exploration Engineering(Rock & Soil Drilling and Tunneling), 2011, 38(10): 1-5.
[2] 张金昌, 刘秀美. 13 000 m科学超深井钻探技术[J]. 探矿工程(岩土钻掘工程), 2014, 41(9): 1-6.
ZHANG Jinchang, LIU Xiumei.13 000 m drilling technology of super-depth scientific drilling-well[J]. Exploration Engineering(Rock & Soil Drilling and Tunneling), 2014, 41(9): 1-6.
[3] CRIDER J G. The initiation of brittle faults in crystalline rock[J]. Journal of Structural Geology, 2015, 77: 159-174.
[4] 姜立春, 王玉丹, 赵奎. 深部高应力空区拱架效应与采场结构尺寸的相依性[J]. 中南大学学报(自然科学版), 2018, 49(10): 2576-2583.
JIANG Lichun, WANG Yudan, ZHAO Kui. Dependence between goaf arching effect and its structure size under high stress[J]. Journal of Central South University(Science and Technology), 2018, 49(10): 2576-2583.
[5] 林鸣, 付宏渊, 颜东煌. 考虑温度与时变因素耦合的混凝土桥梁增量分析方法[J]. 中南大学学报(自然科学版), 2017, 48(9): 2506-2512.
LIN Ming, FU Hongyuan, YAN Donghuang. Incremental analysis considering coupling temperature and time-dependent effects of concrete bridge[J]. Journal of Central South University(Science and Technology), 2017, 48(9): 2506-2512.
[6] MALAN D F. Simulation of the time-dependent behavior of excavations in hard rock[J]. Rock Mechanics and Rock Engineering, 2002, 35(4): 225-254.
[7] KUMARI W G P, RANJITH P G, PERERA M S A, et al. Hydraulic fracturing under high temperature and pressure conditions with micro CT applications: geothermal energy from hot dry rocks[J]. Fuel, 2018, 230: 138-154.
[8] JAMSHIDI E, AMANI M. Numerical wellbore stability analysis using discrete element models[J]. Petroleum Science and Technology, 2014, 32(8): 974-982.
[9] TOMAC I, GUTIERREZ M. Micromechanics of hydro-thermo-mechanical processes in rock accounting for thermal convection[J]. Journal of Engineering Mechanics, 2019, 145(8): 04019055.
[10] CAO Wenke, DENG Jingen, YU Baohua, et al. Offshore wellbore stability analysis based on fully coupled poro-thermo-elastic theory[J]. Journal of Geophysics and Engineering, 2017, 14(2): 380-396.
[11] 肖志强, 贾善坡, 亓宪寅, 等. 流-固-化耦合条件下硬脆性泥页岩井壁渐进破坏效应探讨[J]. 中南大学学报(自然科学版), 2019, 50(10): 2464-2480.
XIAO Zhiqiang, JIA Shanpo, QI Xianyin, et al. Hydraulic-mechanical-chemical coupling evaluation for progressive failure of hard brittle shale wellbore[J]. Journal of Central South University(Science and Technology), 2019, 50(10): 2464-2480.
[12] CHENG Wan, JIANG Guosheng, LI Xiaodong, et al. A porochemothermoelastic coupling model for continental shale wellbore stability and a case analysis[J]. Journal of Petroleum Science and Engineering, 2019, 182: 106265.
[13] 汤盛显, 李亮. 基于Mohr-Coulomb准则的应变软化浅埋隧道围岩弹塑性解[J]. 铁道科学与工程学报, 2019, 16(11): 2775-2781.
TANG Shengxian, LI Liang. Elasto-plastic solution of shallow tunnel considering strain-softening characteristics based on Mohr-Coulomb criterion[J]. Journal of Railway Science and Engineering, 2019, 16(11): 2775-2781.
[14] 李红, 郭孔辉, 宋晓琳, 等. 基于Matlab的多约束自动平行泊车轨迹规划[J]. 中南大学学报(自然科学版), 2013, 44(1): 101-107.
LI Hong, GUO Konghui, SONG Xiaolin, et, al. Trajectory planning of automatic parallel parking with multi-constraints based on Matlab[J]. Journal of Central South University(Science and Technology), 2013, 44(1): 101-107.
[15] BAGDELI M, MANSHAD A K, SHADIZADEH S R, et al. Natural fracture characterization and wellbore stability analysis of a highly fractured southwestern Iranian oilfield[J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 123: 104101.
[16] 杨跃辉, 孙东生, 郑秀华, 等. 岩芯直径变形分析法及其在松科2井深部地应力调查中的应用[J]. 中南大学学报(自然科学版), 2019, 50(12): 3106-3113.
YANG Yuehui, SUN Dongsheng, ZHENG Xiuhua, et al. A method of diametrical core deformation analysis and its application on stress investigation in SK2 Well[J]. Journal of Central South University(Science and Technology), 2019, 50(12): 3106-3113.
[17] 金衍, 陈勉. 井壁稳定力学[M]. 北京: 科学出版社, 2012: 5-15.
JIN Yan, CHEN Mian. Wellbore stability mechanics[M]. Beijing: Science Press, 2012: 5-15.
[18] 王晓. 川西新场地区须家河组水平井井壁稳定性研究[D]. 成都: 成都理工大学, 2011: 10-23.
WANG Xiao. Study on horizontal well borehole stability of Xinchang Xujiahe formation in West Sichuan[D]. Chengdu: Chengdu University of Technology, 2011: 10-23.
[19] 胡继良, 陶士先, 单文军, 等. 超深井高温钻井液技术概况及研究方向的探讨[J]. 地质与勘探, 2012, 48(1): 155-159.
HU Jiliang, TAO Shixian, SHAN Wenjun, et al. Overview of ultra-deep well high-temperature drilling fluid technology and discussion of its research direction[J]. Geology and Exploration, 2012, 48(1): 155-159.
[20] 李亚琛, 段晨阳, 郑秀华. 高温地热钻井的最佳实践[J]. 地质与勘探, 2016, 52(1): 173-181.
LI Yachen, DUAN Chenyang, ZHENG Xiuhua. Best practices for high temperature geothermal drilling[J]. Geology and Exploration, 2016, 52(1): 173-181.
[21] 贾利春, 陈东, 黄兵. 温度对岩石力学特性及井壁稳定性的影响[J]. 钻采工艺, 2017, 40(5): 15-18.
JIA Lichun, CHEN Dong, HUANG Bing. Effects of temperature on rocks mechanics and wellbore stability[J]. Drilling & Production technology, 2017, 40(5): 15-18+2.
[22] 常德玉, 李根生, 沈忠厚, 等. 深井超深井井底应力场[J]. 石油学报, 2011, 32(4): 697-703.
CHANG Deyu, LI Gensheng, SHEN Zhonghou, et al. The stress field of bottom hole in deep and ultra2deep wells[J]. Acta Petrolei Sinica, 2011, 32(4): 697-703.
(编辑 陈灿华)
收稿日期： 2020 -06 -07; 修回日期： 2020 -08 -18
基金项目(Foundation item)：湖南省高新技术产业科技创新引领计划项目(2020GK2067)；湖南省自然科学基金资助项目(2020JJ5707)；有色金属成矿预测与地质环境监测教育部重点实验室开放基金资助项目(2019YSJS16)；自然资源部深部地质钻探技术重点实验室开放基金资助项目(KF201901)；长沙市自然科学基金资助项目(kq2007023) (Project(2020GK2067) supported by the Science and Technology Innovation Leading Program of High-tech Industry of Hunan Province; Project(2020JJ5707) supported by the Natural Science Foundation of Hunan Province; Project(2019YSJS16) supported by the Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring, Ministry of Education; Project(KF201901) supported by the Open Fund of Key Laboratory of Deep Geodrilling Technology of the Ministry of Natural Resources; Project(kq2007023) supported by Natural Science Foundation of Changsha City)
通信作者：隆威，硕士，教授，从事钻井、顶管、探测等研究；E-mail:Lwcsu@sina.com
引用格式： 王李昌, 朱自强, 雷家蔚, 等. TM耦合下科钻深井结晶岩井壁失稳力学响应规律[J]. 中南大学学报(自然科学版), 2021, 52(2): 465-477.
Citation: WANG Lichang, ZHU Ziqiang, LEI Jiawei, et al. Mechanical responses to wellbore instability of crystalline rocks in scientific deep well during thermo-mechano coupling[J]. Journal of Central South University(Science and Technology), 2021, 52(2): 465-477.
