J. Cent. South Univ. (2016) 23: 1961-1969

DOI: 10.1007/s11771-016-3253-3

A bearing fault diagnosis method based on sparse decomposition theory

ZHANG Xin-peng(张新鹏), HU Niao-qing(胡茑庆), HU Lei(胡雷), CHEN Ling(陈凌)

Laboratory of Science and Technology on Integrated Logistics Support, National University of

Defense Technology, Changsha 410073, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: The bearing fault information is often interfered or lost in the background noise after the vibration signal being transferred complicatedly, which will make it very difficult to extract fault features from the vibration signals. To avoid the problem in choosing and extracting the fault features in bearing fault diagnosing, a novelty fault diagnosis method based on sparse decomposition theory is proposed. Certain over-complete dictionaries are obtained by training, on which the bearing vibration signals corresponded to different states can be decomposed sparsely. The fault detection and state identification can be achieved based on the fact that the sparse representation errors of the signal on different dictionaries are different. The effects of the representation error threshold and the number of dictionary atoms used in signal decomposition to the fault diagnosis are analyzed. The effectiveness of the proposed method is validated with experimental bearing vibration signals.

Key words: fault diagnosis; sparse decomposition; dictionary learning; representation error

1 Introduction

Considering the material defects, manufacturing errors, working conditions and other factors like fatigue, aging etc., the damages and faults of the rotating machinery occur inevitably during operation. The bearing is one of the most common and most important key components of the rotating machinery. In case of failure, this will lead to the equipment downtime which affects productivity and results in economic loss. Moreover, it might lead to accidents with extreme danger, which will threaten the safety of the entire equipment, even the staff. Thus, it is particularly important for rotating machinery to execute bearing condition monitoring and fault diagnosis.

For bearing fault diagnosis based on vibration signals, the traditional methods are achieved mainly by the ways like time-domain analysis, frequency domain analysis and time-frequency domain analysis etc [1-5]. In Ref. [6], a novel fault feature extraction method based on the local mean decomposition technology and multi- scale entropy is proposed. The local mean decomposition method, which is a new self-adaptive time-frequency method, is used as a pretreatment to decompose the non-stationary vibration signal of a roller bearing into a number of product functions. Reference [7] presents a new time-frequency manifold feature by combining the time-frequency distribution and the non linear manifold for an effective quantitative representation of machinery health pattern. In Ref. [8], an adaptive data-driven analysis approach called generalized empirical mode decomposition (GEMD) was proposed by defining several baselines. Compared with the original empirical mode decomposition, the components derived from GEMD are more accurate and have the advantages of restrained boundary effect and suppressed mode mixing, as well as precise instantaneous frequency and instantaneous amplitude. In Ref. [9], an effective bearing faults detection algorithm is developed by employing several advanced signal processing techniques as Cepstrum whitening, minimum entropy deconvolution, optimized spectral kurtosis and envelope analysis, which can effectively detect both inner race fault and outer race fault of the planetary bearing. Considering that most of the existing time series methods of feature extraction involve complex algorithm and the extracted features are affected by sample size and noise, a simple time series method for bearing fault feature extraction using singular spectrum analysis of the vibration signal was proposed in Ref. [10], which is used for the decomposition of the acquired signals into an additive set of principal components. A new approach for the selection of the principal components was also presented. To solve the problem of bearing diagnosis under varying rotational speed without a tachometer, a fault characteristic order approach was presented in Ref. [11]. This approach combines the principles of order analysis and resonance demodulation which are respectively among the most effective approaches in dealing with the problem of changing rotational speed and fault diagnosis for rolling element bearings. In Ref. [12], several different feature models are used in a single pool, together with feature selection to optimize the fault diagnosis system. The feature models are based on the complex envelope spectrum, statistical time-domain and frequency-domain parameters, and wavelet packet analysis. Feature selection is achieved by conventional search of the feature space by greedy methods. For final fault diagnosis, the k-nearest neighbor classifier, feedforward net, and support vector machine are used. Reference [13] deals with the discrimination between conditions of faults in rolling element bearings based on the linear discriminant analysis as part of the global spectral analysis, with which spectral features with significant discriminatory power can be obtained. These features are extracted from the envelope spectra of vibration signals without prior knowledge of the bearings specific parameters and the characteristic frequencies. In Ref. [14], a new diagnostic approach was proposed which combines envelope analysis, time synchronous resampling, and spectral averaging of vibration signals to extract condition indicators used for rolling-element bearing fault diagnosis and is validated to be effective for the bearing fault types as inner race, outer race, ball, and cage. In Ref. [15], a novel method of fault diagnosis for bearings was proposed, which accumulates all or part of sub-band signals’ envelope spectrums at a given level in wavelet packet rather than demodulates one selected frequency sub-band signal.

The most information used in these methods would be the bearing structural parameters and the characteristics of the current bearing operating state [16-19]. The bearing fault information will be often interfered or lost in the background noise after the vibration signal being transferred complicatedly, which will make it very difficult to extract fault features from the vibration signals, especially online, and then inevitably affect the fault diagnosis results. To solve this problem, the possibility is considered from another perspective, namely, avoiding fault features extraction directly. For this consideration, a bearing fault diagnosis method based on sparse decomposition theory is proposed. In this method, several over-complete dictionaries corresponded to different bearing states are trained by dictionary learning method using the historical operating data of the bearings. Each of these dictionaries can be effective in signal sparse decomposition for a particular state. While the signals corresponded to other states can not be decomposed sparsely. According to this difference, the bearing states can be identified by comparing the signal sparse representation errors on these different dictionaries. Therefore, the proposed method will avoid the problem in fault features extraction, and has advantages in on-line fault diagnosis. The experimental results demonstrate the effectiveness of the proposed method.

2 Sparse decomposition theory

In order to describe the signal more flexibly, briefly and adaptively, COIFMAN and WICKERHAUSER [20] proposed the concept of signal sparse decomposition in 1992. According to the sparse decomposition theory, the decomposition result would be closer to the nature or intrinsic structure of the signal if the signal can be decomposed more sparsely. The essential characteristics of the signal can be effectively extracted from the sparse representation (decomposition) result, which would be an advantage to the subsequent signal processing and could reduce the signal processing costs essentially. Therefore, in the digital signal processing, the original signal is always described as the corresponded sparse representation in some domain. Currently, the sparse decomposition theory is widely used in the fields of signal processing and image processing [21], such as the radar imaging processing, image compression, audio signal compression, video signal compression, noise suppression, blind source separation, automatic control, seismic data processing, system identification, outline recognition, face recognition.

For an over-complete set G={g_k| k=1, 2, …, K}, where the K elements in G are unit vectors spanning the entire Hilbert space H=R^N; if K>N, then the set G is called over-complete dictionary, whose elements are called atoms.

For any signal f∈H, m atoms in G are selected to represent the signal, viz.,

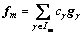                               (1)

where I_m is the suffix set of the atoms g_γ. Define the representation error as

                      (2)

Since m is much smaller than N (the dimension of the space H), the representation defined in Eq. (1) can be called signal sparse representation, and c={c_γ , γ∈I_m} would be called the sparse representation coefficients of the signal f on the dictionary G. The sparse representation coefficients c can be calculated by Matching Pursuit (MP) algorithm or other algorithms [22]. Arranging the atoms (vectors) in over-complete dictionary G as a matrix D, then Eq. (1) can be written in matrix form as

                                  (3)

Obviously, the sparse representation error of the signal is affected directly by the over-complete dictionary. According to the difference of the applications, over-complete dictionaries can be divided into two categories: fixed dictionaries which can be used for non-specific signals and trained dictionaries which are only used for specific signal. Generally speaking, the fixed dictionary can be used for many different kinds of signals, but it is difficult to decompose the signal very sparsely and the signal representation error would be large. While the trained dictionary can decompose the signal sparsely since the structure and characteristics information of the training samples is used in dictionary learning process; therefore, the signal sparse representation result can be very good. However, it can be used only for the signals which have the same state with the training samples. The most frequently used dictionary learning methods are the MOD (method of optimal directions) [23] and the K-SVD (K-singular value decomposition) method [24], and so on. In this work, the over-complete dictionaries corresponded to different states will be trained using the K-SVD as the dictionary learning method.

3 Fault diagnosis method

According to the sparse decomposition theory in Section 2, it can be known that the over-complete dictionary trained by the samples corresponded to some specific state has the good ability to decompose the signals sparsely which have the same state with the training samples. While for the signals corresponded to other states, the dictionary cannot decompose them sparsely. Taking the normal state, the inner ring fault, the outer ring fault and the rolling element fault of a bearing for example, and then 100 vibration signal samples corresponded to each state respectively can be obtained. The data length of each sample is 512 (data source from [25], 6205-2RS JEK SKF deep groove ball bearing, the sampling frequency is 12 kHz). For the samples corresponded to the four states mentioned above, the number of the atoms involved in the decomposition is set to 10 and the mean values of the sparse representation errors on different dictionaries are calculated. The results are shown in Table 1, where D_normal, D_inner, D_outer and D_ball are the over-complete dictionaries corresponded to the normal state, the inner ring fault state, the outer ring fault state and the rolling element fault state respectively. The parameters in dictionary learning method (K-SVD) are set as follows. The quantity of atoms is set to 1024. Thesparsity is set to 10. The number of loops is set to 20. The initial dictionary is selected from the training samples.

Table 1 Mean errors of signal sparse representation on different dictionaries

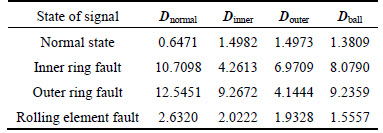
As can be seen from Table 1, compared to the dictionaries corresponded to other states, the sparse representation error of the vibration signal on the dictionary which has the same state with the signal is the smallest. Therefore, this characteristic can be used to achieve the bearing fault diagnosis. The bearing fault diagnosis method based on signal sparse decomposition is proposed and shown in Fig. 1. The main steps are as follows.

1) Acquiring the vibration signals corresponded to different bearing states (including normal state, fault state 1, fault state 2, …, and fault state n) as the training samples;

2) Training the over-complete dictionaries (D₀, D₁, D₂, …, D_n) corresponded to the normal state, fault state 1, fault state 2, …, and fault state n respectively with some appropriate dictionary learning method;

3) Setting the thresholds of sparse representation errors (τ₀, τ₁, τ₂, …, τ_n) corresponded to the bearing normal state, fault state 1, fault state 2, …, and fault state n according to the prior knowledge;

4) Decomposing the test signal x on all the known dictionaries (D₀, D₁, D₂, …, D_n) respectively, and calculating the corresponding sparse representation coefficient vectors c₀, c₁, c₂, …, c_n with MP algorithm. Then the corresponding sparse representation errors (δ₀, δ₁, δ₂, …, δ_n) can be solved as δ_*=||x-D_*·c_*||₂. Finding the smallest one of these errors as the δ, viz. δ=min{δ₀, δ₁, δ₂, …, δ_n};

5) Estimating the state of the bearing:

When δ=δ₀ and δ≤τ₀, the bearing is determined in the normal state; When δ=δ_i and δ≤τ_i, i∈{1, 2, …, n}, the bearing is determined in fault state i; When δ can not satisfy any one of the above terms, we determine the bearing in some unknown state.

In the diagnostic process shown in Fig. 1, we determined the bearing in an unknown state when we can confirm that the bearing is in fault state but not a known fault state. In fact, if more samples corresponded to different fault states can be acquired, then we can get more dictionaries by training, which can be used to recognize the unknown bearing state. The dictionaries corresponded to different states play a role similar to a sieve, which can filter the signals with the corresponding state and achieve the identification of the bearing state ultimately. For the thresholds of sparse representation errors (τ₀, τ₁, τ₂, …, τ_n) corresponded to different states, they can be set according to the prior knowledge.

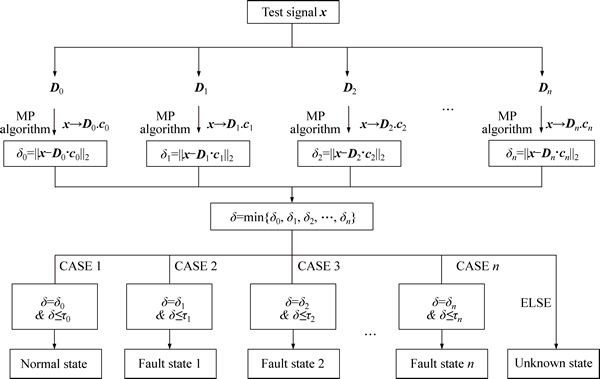
Fig. 1 Flow chart of bearing fault diagnosis method based on signal sparse decomposition

The reason for setting different thresholds of sparse representation errors is that there have many different types of bearing faults, and it is impossible to obtain enough dictionaries by training to describe all the possible bearing states. For some signal which is not in any one of the known states, if decomposing this signal on all the known dictionaries (D₀, D₁, D₂, …, D_n), then the minimum value in all the corresponding sparse representation errors (δ₀, δ₁, δ₂, …, δ_n) can be found consequentially. If we don’t restrict this value and determine the bearing state according to this value directly, then the signal state must be judged as the one of the n+1 known states (the normal state, the fault state 1, the fault state 2, …, and the fault state n). However, according to the foregoing assumption, this signal does not belong to any one of the above-described states, which will result in a misjudgment to the type of the fault. Therefore, the thresholds of sparse representation errors (τ₀, τ₁, τ₂, …, τ_n) are introduced to restrict the minimum value, that is, the bearing state can be determined only when both of the following conditions satisfied.

1) The error δ is the smallest one of all the sparse representation errors;

2) The error δ could not be greater than the corresponding threshold of the signal sparse representation error.

The proposed fault diagnosis method will be validated in next section.

4 Experimental test

The proposed fault diagnosis method is validated using the vibration signals from the 6205-2RS JEK SKF deep groove ball bearings (data sources from [25], and the signal sampling frequency is 12 kHz). Firstly, the over-complete dictionaries corresponded to different states are trained with the training samples. The data length of each training sample is 512. The training samples can be divided into four categories: normal state samples, inner ring fault samples, outer ring fault samples and rolling element fault samples. Each type of the samples contained 20480 signals, which can also be divided into four groups and each group contains 5120 signals according to different motor speeds and loads. The training samples are shown in Table 2.

Then the over-complete dictionaries (D_normal, D_inner, D_outer and D_ball) corresponded to the normal state, the inner ring fault, the outer ring fault and the rolling element fault can be trained respectively by K-SVD dictionary learning method using the above training samples. The parameters in dictionary learning are set as follows. The quantity of atoms is set to 1024. The sparsity is set to 10. The number of loops is set to 20, and the initial dictionary is selected from the training samples.

In order to set the appropriate error thresholds, parts of the training samples in Table 2 on the four known dictionaries are decomposed. The number of the atomsinvolved in the decomposition is set to 10 and the sparse representation errors of the signals with different states on different dictionaries are calculated. The results are shown in Fig. 2.

Table 2 Training samples

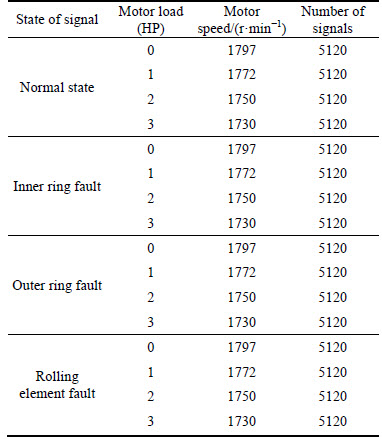
Figure 2(a) shows the sparse representation errors of the normal state signals on the four dictionaries (D_normal, D_inner, D_outer and D_ball) respectively. Figure 2(b) shows the sparse representation errors of the inner ring fault signals on the four dictionaries respectively. Figure 2(c) shows the sparse representation errors of the outer ring fault signals on the four dictionaries respectively. Figure 2(d) shows the sparse representation errors of the rolling element fault signals on the four dictionaries respectively. The data in each figure can be divided into two parts. The data covered by the shadow area indicate the sparse representation errors on the dictionary corresponded to the same state with the current signals. The other parts of the data in the figure describe the sparse representation errors of the signals on other dictionaries.

According to the prior knowledge shown in Fig. 2, the error thresholds (τ_normal, τ_inner, τ_outer and τ_ball) corresponded to the normal state, the inner ring fault, the outer ring fault and the rolling element fault can be set as 1.0, 6.2, 7.2 and 1.8, respectively, which are also shown in Fig. 2 by the black lines. The general principle of setting the threshold is that the threshold value should be greater than most of the errors in the shadow area; meantime, it should be also less than the majority of the errors in the non-shaded area.

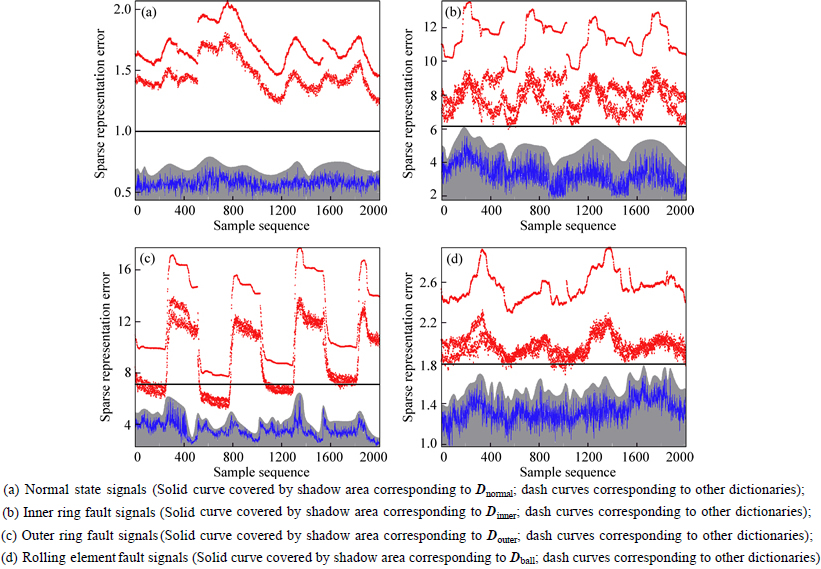
Fig. 2 Sparse representation errors of signals with different states on different dictionaries:

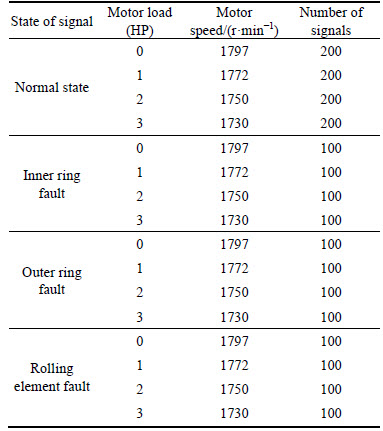
The test samples contain 800 signals corresponded to normal state and 1200 signals corresponded to fault state. The fault can be divided into three categories: the inner ring fault, the outer ring fault and the rolling element fault. For each type of fault, 400 signals were acquired. In accordance with different motor speeds and loads, the test samples corresponded to each bearing state contain four groups of signals, as shown in Table 3. The faults were designed as single point in inner ring, outer ring and rolling element, which were introduced to the test bearings using electro-discharge machining with fault diameter of 0.5334 mm (0.021 inch) and fault depth of 0.2794 mm (0.011 inch).

Table 3 Test samples

The fault diagnosing model is established based on the proposed method in Section 3, where the number of the atoms involved in signal decomposition is set to 10, and the error thresholds are set as follows. The threshold τ_normal is set to 1.0; the threshold τ_inner is set to 6.2; the threshold τ_outer is set to 7.2 and the threshold τ_ball is set to 1.8. Analyzing the test samples in Table 3 and recognizing the corresponding state, the fault diagnosing results are shown in Table 4. It can be seen from Table 4 that the recognition rates of the proposed method to normal state and inner ring fault reach 100%, and to the outer ring fault and rolling element fault, the recognition rates can be up to 99.75% and 91.75% respectively. Meanwhile, the samples which can not be identified correctly are determined to be in some unknown fault state. These results validate the effectiveness of the proposed method to the bearing fault diagnosing.

Table 4 Fault diagnosing results

According to the theory and process of the fault diagnosis method used above, the thresholds of the sparse representation errors have a significant impact on the diagnosing results. Figure 3 shows the recognition rates of the fault diagnosis method to the four bearing states in Table 3 when the corresponding error thresholds change. Figure 3(a) shows the recognition rate to the normal state when the error threshold τ_normal changes. Figure 3(b) shows the recognition rate to the inner ring fault when the error threshold τ_inner changes. Figure 3(c) shows the recognition rate to the outer ring fault when the error threshold τ_outer changes. Figure 3(d) shows the recognition rate to the rolling element fault when the error threshold τ_ball changes.

It can be seen from Fig. 3 that with the increase of the error thresholds, the recognition rates of the proposed method to the four bearing states will increase gradually. However, it should be noticed that the thresholds should not be very large, although a larger threshold can improve the recognition rate to the corresponding state. A very large threshold will increase the possibility of the misjudging when the fault signal is determined to be in some unknown state. In next test, 400 signals corresponded to outer ring fault state in Table 3 were taken as the test samples. Suppose that only three over-complete dictionaries as D_normal, D_inner and D_ball were obtained by training, the desired results should be that all of these 400 test samples are determined to be in some unknown faults according to the proposed method; otherwise, the results should be incorrect. Keeping the threshold τ_normal as 1.0 and τ_ball as 1.8, the misjudging rates can be calculated when the threshold τ_in changes. The misjudging rate is defined as the ratio of the number of the misjudged samples to the total number of the test samples. The number of the atoms used in the signal decomposition is set to 10 and the fault diagnosing results are shown in Fig. 4. It can be seen from Fig. 4 that with the increase of the error threshold τ_innre, the misjudging rate will increase gradually (in fact, most of the misjudged samples are determined to be in inner ring fault), which would be a disadvantage to the fault diagnosing result. Therefore, we should make full use of the prior knowledge to set the thresholds of the sparse representation errors appropriately, viz. not too small or too big.

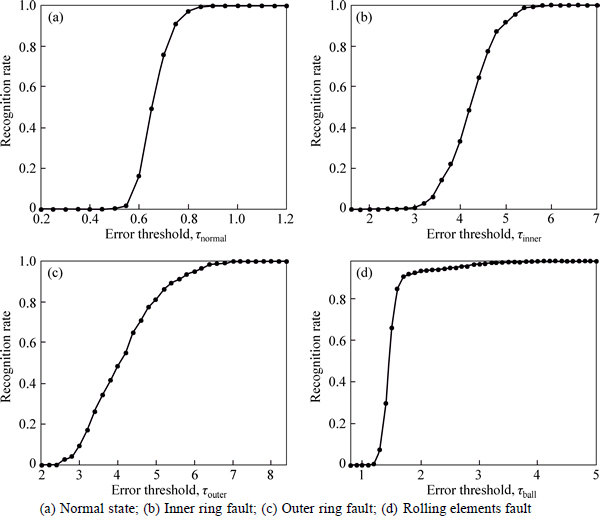
Fig. 3 Recognition rates to bearing states in different error thresholds:

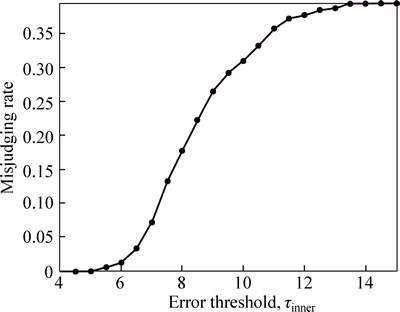
Fig. 4 Misjudging rate to bearing state in different error threshold τ_in

In the foregoing tests, the number of the atoms involved in signal decomposition or reconstruction was kept at 10 all the time. According to the fault diagnosis theory in this work, the number of the atoms used to decompose the signal affects the sparse representation errors directly. Finally, the fault diagnosing results will be also affected. Similar to the previous tests, the thresholds of sparse representation error are kept as follows. The threshold τ_normal is set to 1.0; the threshold τ_inner is set to 6.2; the threshold τ_outer is set to 7.2 and the threshold τ_ball is set to 1.8. The recognition rates to the different states are calculated using different numbers of atoms to decompose the signal. The fault diagnosing results are shown in Fig. 5.

As can be seen from Fig. 5, with the atoms used in signal decomposition increasing, the recognition rates to all the bearing states will gradually increase. For the signals which have the same state with the dictionary,more atoms involved in signal decomposition will be helpful to accurately reconstruct the signals, and then the reconstruction error will be smaller. While for the signals corresponded to other states, since the dictionary can not decompose them sparsely, more atoms could not improve the reconstruction results of these signals significantly. According to the fault diagnosis theory, this difference would be an advantage to the state identification. Therefore, with the increase of the atoms involved in decomposition, the fault diagnosing results improve gradually. It should be noticed that more atoms used in signal decomposition lead to more computational cost. Too much computation should be a disadvantage to bearing fault diagnosis. Therefore, the number of the atoms used in decomposition should have a moderate size, which can be chosen by referring the sparsity set in dictionary learning. Generally, the number of the atoms can be set as the value which is equal to the sparsity used in dictionary learning, just as what we did in this work.

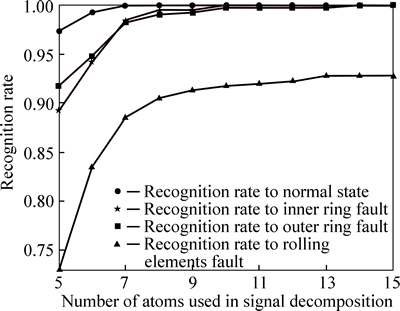
Fig. 5 Recognition rates to different states with different numbers of atoms in signal decomposition

5 Conclusions

1) The proposed method based on the signal sparse representation theory can be achieved effectively in bearing fault diagnosis by avoiding the problem in choosing and extracting the proper fault features.

2) In the proposed method, a bigger threshold can effectively improve the recognition rate to each bearing state, while it should not be set too big; otherwise, it will lead to the increase of the misjudging rate.

3) The number of the atoms involved in signal decomposition can be decided by referring to the sparsity set in dictionary learning.

4) According to the theory of the fault diagnosis method in this work, the more the types of dictionaries obtained by training are, the more the fault states can be identified. A good dictionary is propitious to decompose the signal more sparsely, and the quality of the dictionary will affect the signal sparse representation error directly, thereby affect the final fault diagnosing results. Therefore, how to get abundant and outstanding over-complete dictionaries will be one of the important works in our further research.

Acknowledgements

The authors gratefully acknowledge the Bearing Data Center of Case Western Reserve University to provide the bearing test data. Valuable comments on the work from anonymous reviewers are very much appreciated.

References

[1] RAJ A S, MURALI N. A novel application of Lucy–Richardson deconvolution: Bearing fault diagnosis [J]. Journal of Vibration and Control, 2015, 21(6): 1055-1067.

[2] LIU Tao, CHEN Jin, DONG Guang-ming, XIAO Wen-bing, ZHOU Xu-ning. The fault detection and diagnosis in rolling element bearings using frequency band entropy [J]. Journal of Mechanical Engineering Science, 2012, 27(1): 87-99.

[3] LV Yong, ZHU Qing-lin, YUAN Rui. Fault diagnosis of rolling bearing based on fast nonlocal means and envelop spectrum [J]. Sensors, 2015, 15(1): 1182-1198.

[4] MA Jun, WU Jian-de, YUAN Xu-yi. The fault diagnosis of the rolling bearing based on the LMD and time-frequency analysis [J]. International Journal of Control & Automation, 2013, 6(4): 357-376.

[5] YU Ling-li, CAI Zi-xing, ZHOU Zhi, FENG Zhen-qiu. Fault detection and identification for dead reckoning system of mobile robot based on fuzzy logic particle filte [J]. Journal of Central South University, 2012, 19: 1249-1257.

[6] LIU Huan-huan, HAN Ming-hong. A fault diagnosis method based on local mean decomposition and multi-scale entropy for roller bearings [J]. Mechanism and Machine Theory, 2014, 75: 67-78.

[7] HE Qing-bo. Time–frequency manifold for nonlinear feature extraction in machinery fault diagnosis [J]. Mechanical Systems and Signal Processing, 2013, 35: 200-218.

[8] ZHENG Jin-de, CHENG Jun-sheng, YANG Yu. Generalized empirical mode decomposition and its applications to rolling element bearing fault diagnosis [J]. Mechanical Systems and Signal Processing, 2013, 40: 136-153.

[9] FAN Zhi-qi, LI Huai-zhong. A hybrid approach for fault diagnosis of planetary bearings using an internal vibration sensor [J]. Measurement, 2015, 64: 71-80.

[10] MURUGANATHAM B, SANJITH M A, KRISHNAKUMAR B, SATYAMURTY S A V. Roller element bearing fault diagnosis using singular spectrum analysis [J]. Mechanical Systems and Signal Processing, 2013, 35: 150-166.

[11] WANG Tian-yang, LIANG Ming, LI Jian-yong, CHENG Wei-dong. Rolling element bearing fault diagnosis via fault characteristic order (FCO) analysis [J]. Mechanical Systems and Signal Processing, 2014, 45: 139-153.

[12] THOMAS W R, FRANCISCO A B, F M. Heterogeneous feature models and feature selection applied to bearing fault diagnosis [J]. IEEE Transactions on Industrial Electronics, 2015, 62(1): 637-646.

[13] HARMOUCHE J, DELPHA C, DIALLO D. Improved fault diagnosis of ball bearings based on the global spectrum of vibration signals [J]. IEEE Transactions on Energy Conversion, 2015, 30(1): 376-383.

[14] HECKE B V, QU Y Z, HE D, BECHHOEFER E. A new spectral average-based bearing fault diagnostic approach [J]. J Fail Anal and Preven, 2014, 14: 354-362.

[15] JIANG Rui-hong, LIU Shu-lin, TANG You-fu, LIU Ying-hui. A novel method of fault diagnosis for rolling element bearings based on the accumulated envelope spectrum of the wavelet packet [J]. Journal of Vibration and Control, 2015, 21(8): 1580-1593.

[16] LI Mao-lin, LIANG Lin, WANG Sun-an. Sensitive feature extraction of machine faults based on sparse representation [J]. Journal of Mechanical Engineering, 2013, 49(1): 73-79. (in Chinese)

[17] WANG Guo-biao, HE Zheng-jia, CHEN Xue-feng, LAI Yi-nan. Basic research on machinery fault diagnosis—What is the prescription [J]. Journal of Mechanical Engineering, 2013, 49(1): 63-72. (in Chinese)

[18] ZENG Qing-hu, QIU Jing, LIU Guan-jun, TAN Xiao-dong. Application of wavelet correlation feature scale entropy to fault diagnosis of roller bearings [J]. Journal of National University of Defense Technology, 2007, 29(6): 102-105. (in Chinese)

[19] WANG Bing-cheng, REN Zhao-hui, WEN Bang-chun. Fault diagnoses method of rotating machines based on nonlinear multi- parameters [J]. Journal of Mechanical Engineering, 2012, 48(5): 63-69. (in Chinese)

[20] COIFMAN R, WICKERHAUSER M. Entropy-based algorithms for best basis selection [J]. IEEE Transactions Information Theory, 1992, 38: 1713-1716.

[21] PHILLIPS P J. Matching pursuit filters applied to face identification [J]. IEEE Trans on Image Processing, 1998, 7(8): 1150-1164.

[22] MALLAT S, ZHANG Z. Matching pursuits with time-frequency dictionaries [J]. IEEE Trans on Signal Processing, 1993, 41(12): 3397-3415.

[23] ENGAN K, AASE S O, HAKON-HUSOY J H. Method of optimal directions for frame design [C]// 1999 IEEE Int Conf Acoust, Speech, Signal Process. Phoenix, USA, 1999, 5: 2443-2446.

[24] AHARON M, ELAD M, BRUCKSTEIN A M. K-SVD: An algorithm for designing of overcomplete dictionaries for sparse representation [J]. IEEE Trans on Signal Processing, 2006, 54(11): 4311-4322.

[25] Bearing test data. [2015-03]. ttp://csegroups.case.edu/ bearingdatacenter/pages/download-data-file.

(Edited by YANG Hua)

Foundation item: Projects(51375484, 51475463) supported by the National Natural Science Foundation of China; Project(kxk140301) supported by Interdisciplinary Joint Training Project for Doctoral Student of National University of Defense Technology, China

Received date: 2015-06-15; Accepted date: 2016-01-18

Corresponding author: HU Niao-qing, Professor, PhD; Tel: +86-731-84574971; E-mail: hnq@nudt.edu.cn