DOI: 10.11817/j.issn.1672-7207.2016.09.022

一种基于综合引导的偏好多目标优化算法

戴永彬

(辽宁工业大学 软件学院，辽宁 锦州，121001)

摘要：针对多目标优化的偏好问题，提出一种综合引导的偏好多目标优化粒子群算法(IG-MOPSO)。该算法的核心思想是将多目标优化策略的参考点算法和参考区域算法结合在一起。在参考点移动的过程中，动态调整参考区域面积。经过每一次的迭代计算，该算法可不断调整参考点从而获得更优的偏好解，同时借助参数d控制偏好的范围。另外，采用g-支配改进全局最优粒子的选取方法，提高搜索的有效性。研究结果表明：本文提出的算法是可行、有效的。

关键词：多目标优化；偏好区域；粒子群；综合引导

中图分类号：TP301          文献标志码：A         文章编号：1672-7207(2016)09-3072-07

Preference multi-objective optimization algorithm with integrated guidance

DAI Yongbin

(School of Software, Liaoning University of Technology, Jinzhou 121001, China)

Abstract: A preference multi-objective particle swarm optimization algorithm (IG-MOPSO) with integrated guidance for multi-objective optimization problem was proposed. The main ideas of the algorithm were to combine the notion of reference point with reference region. With the movement of reference points, the area of the reference regions was adjusted dynamically. The reference point was modified by the algorithm to refine the preferences through every iterative calculation, and the parameter d was set to control the reference range simultaneously. By means of g-dominance, the choosing method of best modes of particle swarm optimization was improved, and the effectiveness of the search was also enhanced. The results show that the presented algorithm has good feasibility and effectiveness.

Key words: multi-objective optimization; preference regions; particle swarm; integrated guidance

近年来，随着多目标进化算法的不断发展和完善，基于偏好信息的多目标决策算法的研究成果大量涌现。由于融合了决策者的偏好信息，通过不同的引导方式，进化种群被引导至参考区域。这样，基于偏好信息的多目标决策算法可以忽略对其他解的计算，只需要处理参考区域内的最优解即可，从而改善了算法的效率，减少了计算的负担，是一种优于传统方法的算法。为了实现种群粒子向偏好区域运动，一般进化算法采用3类交互方式^[1]：前决策技术、后决策技术以及交互决策技术。由于交互决策采用一边优化，一边决策的动态执行过程，所以这种交互技术被广泛应用。在交互决策过程中，需要决策者随时提供偏好信息，一般会以参考点、参考区域、参考方向等形式给出。参考点引导方式以参考点作为偏好信息的载体，WIERZBICKI^[2]最先提出参考点方法，该方法利用ASF函数将参考点映射到Pareto前沿上并最终求得有效解，但是每次计算只能获得一个最优解。为此，出现了很多可以获取多个解的参考点引导算法。一般可分为固定参考点和移动参考点2类。固定参考点是指参考点在算法运行时固定不动，一般会以参考点为基础，计算进化粒子与参考点的距离并以此作为粒子选择的标准。DEB等^[3-4]选择与参考点最近的进化粒子进入解集，并提出一种利用参考点提供的方向信息从而获得偏好解集的改进算法。BEN等^[5]提出了一种新的支配关系r-支配，该策略改进了Pareto支配，对互不支配解采取更为严格的偏序关系，可以选择最接近参考点的解。由于该方法的有效性，受到了学界的广泛关注。移动参考点是指在算法进行时不断改变参考点的位置，直到算法结束。WIERZBICKI^[2]提出了一种基于参考点的改进算法，利用偏好向量信息建立新的参考点。MOLINA等^[6]采用g-支配策略并移动参考点从而增加粒子选择压力，同时指引种群向Pareto前沿移动。对参考区域而言，大多数文献将参考区设计成大小固定、形状各异的多面体，一般位置在Pareto前沿附近。参考区引导方式是将解空间的任一点到参考区域距离作为选择粒子的标准，相对于参考点引导，参考区引导更加灵活，计算距离时不必使所有的粒子都指向一个参考点。蒲保兴等^[7]定义的距离是解空间内任意一点到超立方体的最近距离。麦雄发等^[8]定义的距离为目标空间的点到偏好区域的所有顶点的平均距离。另外，刘芳^[9]提出软约束球支配概念，将偏好区域设计成球形。然后，根据距离并借助免疫算法驱动粒子向Pareto前沿移动，最终获取最优解。采用以上这些区域控制方式，算法可以选出最优的进化粒子。综上所述，参考点或参考区域引导方式各自具有不同的特点和不足之处。基于偏好信息的多目标进化算法一般只采用单一的引导方式而有关综合引导方式却不多见。为了兼顾参考点和参考区域引导方式的优点，本文作者将二者结合起来，提出一种综合引导方式。这种综合引导方式控制参考点从初始位置移动到Pareto前沿上，实现偏好方向的准确指引，同时以参考点为中心的参考区域随之移动并在移动过程中自适应调整参考区域的规模和大小，增加粒子选择压力。通过设置参考区域的最小值控制决策的偏好范围，从而获得规模和范围可控的有效解集。为了获取粒子群全局最优粒子，本文作者利用g-支配概念获取偏好信息，实现对整个粒子群的有效引导。通过仿真实验，证明其有效性。

1  基本问题和概念

1.1  多目标问题

多目标为题可描述如下：

Min f(X)={f₁(X), f₂(X), …, f_m(X)}

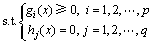          (1)

式中：X为R空间的决策变量；g_i(x)为和h_j(x)分别为不等式约束和等式约束。

多目标优化问题一般很难获得一个满足所有目标的最优解。为此，常采用Pareto解集作为寻优的结果。Pareto解集一般包含若干个解，可以根据决策需要选取Pareto解作为最优解。最优解集的理想状态是解尽量接近Pareto前沿并保证解的均匀分布。

1.2  g-支配概念

g-支配可以通过划分目标空间引导偏好方向，增加选择压力。另外，g-支配很容易和其他多目标算法结合，非常实用。本文采用g-支配实现全局最优粒子的选择，采用Flag_g表示g-支配关系，具体定义如下：

已知2个点w和 w^*∈R^m，只要满足以下2个条件之一就可以称为点w g-支配w^*：

1) Flag_g(w)＞Flag_g(w^*)；

2) w_i≤w_i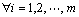^*，，满足Flag_g(w)= Flag_g(w^*)，那么至少存在1个j使w_j＜w_j^*。

Flag_g(w)定义：

       (2)

式中：g为解空间上的参考点；w为解空间的任一点。

2  IG-MOPSO算法

目前，虽然多目标进化算法已经取得了巨大进步，并在多个领域得以应用^[10-13]。但是基于偏好信息的多目标优化算法还有2个方面的问题需要进一步研究和解决：在种群靠近Pareto前沿过程中，如何增加选择压力与加速收敛速度；如何控制偏好区域的规模和偏好范围。为此，本文作者将参考点和参考区域2种引导方式结合起来，提出综合引导的思想。首先，使参考点随着算法的运行从初始点逐步移动到Pareto前沿上。其次，设置参考点为参考区域的中心，参考区域随参考点一齐移动并在移动过程中动态减小参考区域，增加粒子的选择压力。最后，当参考点到达Pareto前沿时，参考区域也同时变为一个最小设定区域，区域内的非支配解即为最优折中解。因此，本文提出的综合引导的方法即可解决选择压力问题，实现对偏好区域的控制，避免有些常规偏好算法，例如文献[5-7]和文献[14]非支配解容易收敛到一点的问题。

2.1  参考区域的设计

由于多目标问题的解空间是一个多维空间，所以在解空间内部的一个区域是一个多面体。为了计算方便，本文参照自适应网格中的超立方体的概念，将参考区域设计成一个自适应变化的超立方体。超立方体空间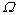的表达式为：

     (3)

式中：x_i为解空间的任意一点；c_i为区域中心点；d为偏好区域规模因子，是超立方体中心到超立方体一个面的距离；m为目标数量。

根据式(3)，在目标空间形成以c_i为中心，d为半径的超立方体，d越大表示参考区域越大，也就是偏好区域的规模越大。在种群初始时，为了使超立方体容纳更多粒子，应该将超立方体设置较大，例如可以根据各粒子的最大、最小目标函数值以及中心点位置来计算d，使超立方体包含所有粒子。

2.2  综合引导的主要方程

综合引导主要包括参考点移动公式和参考区变化公式。这2个公式保证参考点和参考区域向Pareto前沿移动时动态调整。参考点移动的具体公式如下。

1) 移动参考点表达式。

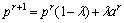            (4)

其中：r为当前运行代数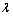；为迭代比例因子；r_max为运行总代数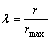；； p^r为参考点；a^r为archive中的非劣解。

2) 偏好区域规模因子d表达式。

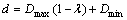            (5)

其中：D_max为偏好规模因子的上限；D_min为偏好规模因子的下限。

2.3  动态引导过程

根据本文提出的参考点和参考区域的移动公式，仅以2目标为例说明综合引导的过程。在种群初始化过程中，将决策者给定的参考点设置为正方形中心并根据各个粒子的最大和最小目标函数值情况确定正方形的D_max。确定D_max的方法很多，例如，首先比较并确定所有粒子的目标函数值f₁，f₂的最小值和最大值并以 f₁=f_1min，f₁=f_1max，f₂=f_2min，f₂=f_2max为边构成一个初始化粒子区域；其次分别计算参考点到区域四边的垂直距离；最后选择最长的距离作为D_max，即可保证D_max决定的区域尽量覆盖所有粒子。当然，也可根据参考点和粒子的具体情况，采用其他方法取得合适的D_max。初始化后，随着算法运行，按照式(4)和式(5)移动参考点，动态减小超正方形面积，逐步增加粒子选择压力。最后，当参考点到达Pareto前沿上时，偏好规模因子d取最小值，在这个正方形区域内的非支配解即为所求，具体见图1所示，图中正方形区域为参考区域初始和停止时的状态，虚线正方形是中间状态。因此，修改偏好规模因子d下限就可以控制偏好范围，同时克服了有些常规偏好多目标算法的非支配解聚集为一点的问题。

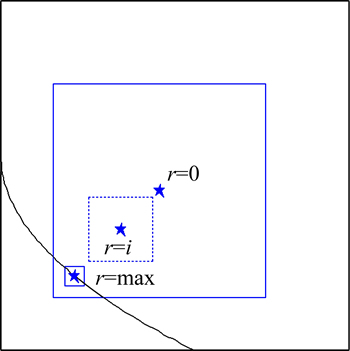
图1  综合引导策略模型

Fig. 1  Preference model of integrated guided strategy

2.4  全局最优粒子的选择

粒子群算法作为一种智能进化算法，近年来发展迅速，已经被广泛应用于各行各业^[15-16]。本文作者利用粒子群算法实现动态综合引导策略。为了保存粒子种群历史最优解，建立archive集，然后，从archive集中选取全局最优粒子，引导整个粒子种群向偏好区域飞行。为了保证全局最优粒子向偏好方向飞行，很多选取全局最优粒子的算法被提出，例如Sigma方  法^[17]、拥挤和收敛距离比值法^[18]、信息熵法^[19]、拉格朗日法^[20]等。但这些方法有的比较复杂，难以执行或者只适用于特定情况。为此，本文采用g-支配概念，将archive的解集进行划分并从中随机选择一个作为全局最优粒子。g-支配的优点之一就是无论参考点是否在可行域都不会影响算法的有效收敛。图2所示为不可行域内g-支配情况，图3所示为可行域内g-支配情况。从图2和图3可知：由实线环绕的Flag₁区域就是按g-支配划分的区域。全局最优粒子可以从处于Flag₁区域的archive粒子中随机选取。

图2  不可行域内支配关系图

Fig. 2  Dominant diagram in infeasible region

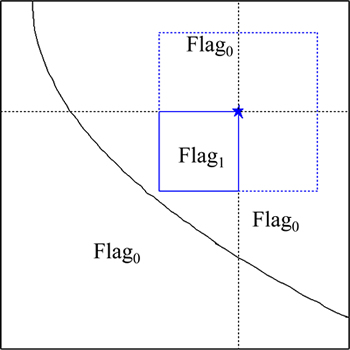
图3  可行域内支配关系图

Fig. 3  Dominant diagram in feasible region

另外，本文采用Pareto占优选择档案粒子，实现外部archive的更新。借助拥挤距离算法对archive进行剪枝。个体最优值可根据个体的占优关系来选取。由于篇幅所限，有关粒子群算法的原理，本文就不再详细介绍^[21]。

3  算法流程

除了以上分析的情况，还应考虑到参考点设置在Pareto前沿上的特殊情况。这时，为了保证偏好区域的准确，将不再移动参考点，可以将参考点作为粒子群全局最优的粒子，引导种群飞行。据此，本文提出的IG-MOPSO算法的流程如下：

1) 初始化。对粒子群主要参数赋值，例如：迭代次数r=0，最大迭代次数r_max，超立方体偏好规模因子的下限D_min等。根据多目标优化的目标数m，随机产生种群数量为N的初始种群，设定archive大小n。

2) 判断参考点是否在Pareto前沿上，如果参考点在Pareto前沿上，设标志变量l=1，否则l=0。

3) 计算种群中各个粒子的多目标适应度。

4) 获取满足式(3)的粒子，利用Pareto占优选择archive粒子。当外部archive中非劣解超过规定数量时，采用拥挤距离方法进行维护。

5) 当l=1时，选择参考点为全局最优粒子；当l=0时，利用g-支配策略划分archive非劣解，从中随机选择全局最优值。然后，利用Pareto占优关系选择个体最优值。

6) 如果l=0时，参考点更新。否则，不更新。

7) 超立方体的偏好规模因子d更新。

8) 粒子种群更新。

9) r=r+1，如果迭代次数小于最大迭代设定值则转到步骤3)，否则结束循环。

4  仿真分析

选取ZDT^[22]和DTLZ^[23]系列的主要测试函数来验证本文提出算法的性能，其中ZDT1~ZDT3和DTLZ2分别测试IG-PSO算法针对Pareto前沿为凸、非凸、不连续和高维时优化的能力。另外，本文将IG-MOPSO算法和比较经典的g-支配算法以及r-支配算法进行了比较和分析。其中，g-支配和r-支配算法采用NSGA-Ⅱ算法框架。相关仿真的基本参数设置为：种群大小为100，档案大小为100，变量维数为30，交叉概率为0.99，变异概率为0.1，最大运行次数为200，r-支配算法的非支配阀值设为0.25。ZDT1，ZDT2和ZDT3的目标维数为2，DTLZ2目标维数为3。测试函数各独立运行20次，c₁=c₂=2，w_q=0.5，c₁和c₂为粒子群算法的学习因子，w_q为粒子群算法的惯性权值。

4.1  收敛性和分布性测试情况

分别采用GD^[24]和SP^[25]作为算法收敛性和分布性能的指标。GD越小，表明算法解的收敛性越好，SP值越小，表明解的分布越均匀。测试函数ZDT1，ZDT2，ZDT3的参考点设置为(0.5,0.5)，DTLZ2的参考点设置为(0.5,0.5,0.5)，本文提出的IG-MOPSO、g-支配算法以及r-支配算法的GD和SP的均值分别如表1和表2所示。

表1  GD计算结果

Table 1  Results of GD computation

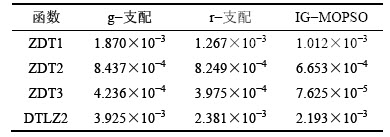
表2  SP计算结果

Table 2  Results of SP computation

由表1和表2可知：r-支配算法的性能比g-支配算法的性能好，主要是因为r-支配算法改进了Perato支配关系，进一步确定了一个非支配解距离参考的远近程度。因此，在控制解集收敛性和分布性方面更具优势。另外，通过以上实验分析可知，在使用二维测试函数ZDT1和ZDT2进行测试时，3种算法的收敛性较平均。但在测试ZDT3时，其Perato前沿是不连续的，g-支配和r-支配与本文提出的IG-MOPSO在收敛性方面有较大差距。从分布性方面看，本文提出的IG-MOPSO算法也接近或优于g-支配算法和r-支配算法的指标。这主要是因为IG-MOPSO算法不仅从交互方式进行了改进，同时也提高了粒子群全局最优的引导能力。因此，本文的IG-MOPSO算法具有较好的收敛性和分布性。

4.2  参考点位置和D_min变化的影响

当综合引导算法的参数发生变化时，选择不同的测试函数进行仿真。利用ZDT1函数进行测试时，参数D_min=0.035，参考点起始位置(0.7,0.6)，测试结果如图4所示。从图4可知：参考点位于可行域。当参考点起始位置为(0.35,0.35)，D_min =0.05，参考点位于不可行域，采用ZDT2函数测试，结果如图5所示。利用测试函数ZDT3检测不连续空间性能，参考点位置为(0.55,0.35)，D_min=0.2，测试效果如图6所示。为了测试参考点设置Pareto前沿上或附近时的算法性能，参考点为(0.5,0.6,0.6)，D_min=0.015，DTLZ2测试的三维效果如图7所示。由图5~7可知：无论参考点位置处于可行域还是不可行域，处于Pareto前沿上或远离前沿，算法都可以得到设定范围内的非劣解。当改变D_min时，算法可以控制偏好范围，获得希望的折中解集。

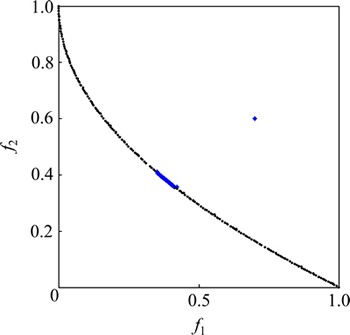
图4  当D_min=0.035时，ZDT1的有效解

Fig. 4  Efficient solutions for ZDT1 with D_min=0.035

图5  当D_min=0.05时，ZDT2的有效解

Fig. 5  Efficient solutions for ZDT2 with D_min=0.05

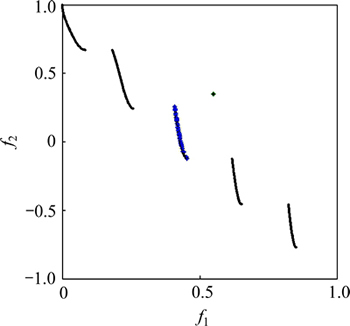
图6  当D_min=0.2时，ZDT3的有效解

Fig. 6  Efficient solutions for ZDT3 with D_min=0.2

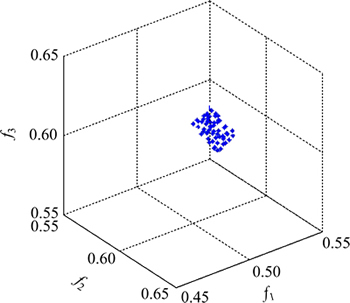
图7  当D_min=0.015时，DTLZ2的有效解

Fig. 7  Efficient solutions for DTLZ2 with D_min=0.015

5  结论

1) 融合了参考点和参考区的优点，提出了一种综合偏好引导策略。当参考点向Pareto前沿逼近时，参考区域不断减小直至区域的下限。这样，便于增加粒子选择压力，同时也控制了偏好区域规模，避免了Pareto解聚集在一点。

2) 采用g-支配获取全局最优引导粒子，可以有效引导粒子种群的飞行。

3) 以ZDT和DTLZ为测试函数进行了仿真测试，通过对仿真结果进行了分析，验证了本文提出算法的有效性和可行性。

参考文献：

[1] COELLO C, CARLOS A. Handling Preferences in evolutionary multi-objective optimization: a survey[C]// Proceedings of the Congress on Evolutionary Computation. La Jolla, USA: IEEE, 2000: 30-37.

[2] WIERZBICKI A P. The use of reference objectives in multi-objective optimization[M]. Berlin: Springer Berlin Heidelberg, 1980: 469–486.

[3] DEB K, SUNDAR J, RAO N U B, et al. Reference point based multi-objective optimization using evolutionary algorithms[J]. International Journal of Computational Intelligence Research, 2006, 2(3): 273-286.

[4] DEB K, KUMAR A. Light beam search based multi-objective optimization using evolutionary algorithms[C]// Proceedings of the Congress on Evolutionary Computation. Singapore: IEEE, 2007: 2125-2132.

[5] BEN-SAID L, BECHIKH S, GHEDIRA K. The r-dominance: a new dominance relation for interactive evolutionary multicriteria decision making[J]. IEEE Transactions on Evolutionary Computation, 2010, 14(5): 801-818.

[6] MOLINA J, SANTANA L V, COELLO C A C, et al. g-dominance: Reference point based dominance for multi- objective metaheuristics[J]. European Journal of Operational Research, 2009, 197(2): 685-692.

[7] 蒲保兴, 杨路明, 谢东. 嵌入决策者偏好区域的多目标优化算法[J]. 小型微型计算机系统, 2009, 1(1): 144-147.

PU Baoxing, YANG Luming, XIE Dong. Multi-objective optimization algorithm embedded by user preference region[J]. Journal of Chinese Computer Systems, 2009, 1(1): 144-147.

[8] 麦雄发, 李玲. 基于决策者偏好区域的多目标粒子群算法研究[J]. 计算机应用研究, 2010, 27(4): 1301-1303.

MAI Xiongfa, LI Ling. Multiobjective particle swarm optimization algorithm based on DMS perference region[J]. Application Research of Computers, 2010, 27(4): 1301-1303.

[9] 刘芳. 基于免疫多目标优化的否定选择算法[D]. 西安: 西安电子科技大学电子工程学院, 2011: 11-35.

LIU Fang. Immune multi-objective optimization based negative selection algorithm[D]. Xi’an: Xi’an University. School of Electronic Engineering, 2011: 11-35.

[10] 段雪妍, 余思勤, 范琛, 等. 基于UTA方法的多目标优化模型[J]. 数学的实践与认识, 2015, 45(23): 138-146.

DUAN Xueyan, YU Siqin, FAN Chen, et al. A multi-objective optimization model based on UTA[J]. Mathematics in Practice and Theory, 2015, 45(23): 138-146.

[11] 章恩泽, 陈庆伟. 改进的r支配高维多目标粒子群优化算法[J] .控制理论与应用, 2015, 32(5): 623-630.

ZHANG Enze, CHEN Qingwei. Improved r-dominance-based particle swarm optimization for multi-objective optimization[J]. Control Theory & Applications, 2015, 32(5): 623-630.

[12] 李章晓, 宋薇, 张兴义. 基于带决策者偏好多目标优化的证券组合投资研究[J]. 合肥师范学院学报, 2015, 33(3): 37-40.

LI Zhangxiao, SONG Wei, ZHANG Xingyi. Stock portfolio based on multi-objective optimization with preference of decision-makers[J]. Journal of Hefei Normal University, 2015, 33(3): 37-40.

[13] 朱海南. 大停电后的机组恢复顺序优化研究[D]. 济南: 山东大学电气工程学院, 2015: 48-58.

ZHU Hainan. Studies on generator start-up sequence after power system major blackout[D]. Jinan: Shandong University. School of Electrical Engineering, 2015: 48-58.

[14] 余进, 何正友, 钱清泉. 基于偏好信息的多目标微粒群优化算法研究[J] .控制与决策, 2009, 24(1): 66-70.

YU Jin, HE Zhengyou, QIAN Qingquan. Study on multiobjective particle swarm optimization algorithm based on preference[J]. Control and Decision, 2009, 24(1): 66-70.

[15] 王万良, 唐宇. 微粒群算法的研究现状与发展[J]. 浙江工业大学学报, 2007, 35(2): 137-138.

WANG Wanliang, TANG Yu. The state of art in particle swarm optimization algorithms[J]. Journal of Zhejiang University of Technology, 2007, 35(2): 137-138.

[16] 程哲, 王伟, 谢广明, 等. 粒子群优化算法及其在机器人技术中的应用[J]. 兵工自动化, 2014, 33(1): 76-81.

CHENG Zhe, WANG Wei, XIE Guangming, et al. Particle swarm optimization algorithm and its application in robotics[J]. Ordnance Industry Automation, 2014, 33(1): 76-81.

[17] 黄敏, 江渝, 毛安, 等. 基于全局最优位置自适应选取与局部搜索的多目标粒子群优化算法[J]. 计算机应用, 2014, 34(4): 1074-1079.

HUANG Min, JIANG Yu, MAO An, et al. Multi-objective particle swarm optimization algorithm based on global best position adaptive selection and local search[J]. Journal of Computer Applications, 2014, 34(4): 1074-1079.

[18] 刘衍民, 牛奔, 赵庆祯. 多目标优化问题的粒子群算法仿真研究[J]. 计算机应用研究, 2011, 28(2): 458-460.

LIU Yanmin, NIU Ben, ZHAO Qingzhen. Particle swarm optimizer simulation research of multi-objective optimization problems[J]. Application Research of Computers, 2011, 28(2): 458-460.

[19] 仲昭明, 李向阳, 逄珊. 混合择优的多目标免疫粒子群优化算法[J]. 计算机工程与应用, 2013, 49(13): 43-47.

ZHONG Zhaoming, LI Xiangyang, PANG Shan. Multi-objective immune particle swarm optimization algorithm with a hybird global best selecting strategy[J]. Computer Engineering and Applications, 2013, 49(13): 43-47.

[20] 何潜, 王岗, 雷雨, 等. 基于改进粒子群优化算法的火电机组负荷多目标优化[J]. 电网技术, 2010, 34(8): 118-122.

HE Qian, WANG Gang, LEI Yu, et al. Improved particle swarm optimization based multi-objective optimization of load dispatching among thermal power units[J]. Power System Technology, 2010, 34(8): 118-122.

[21] KENNEDY J, EBERHART R C. Particle swarm optimization [C]// Proceedings of the IEEE International Conference on Neural Networks. Perth, Australia: IEEE, 1995: 1942-1948.

[22] ZITZLER E, DEB K, THIELE L. Comparison of multi-objective evolutionary algorithms: empirical results[J]. Evolutionary Computation, 2000, 8(2): 173-195.

[23] DEB K, THIELE L, LAUMANNS M, et al. Scalable multi-objective optimization test problems[C]// Proceedings of the Congress on Evolutionary Computation. Honolulu, USA: IEEE, 2002: 825-830.

[24] Van VELDHUIZEN D A, LAMONT G B. Evolutionary computation and convergence to a pareto front[C]// The Late Breaking Papers at the Genetic Programming Conference. California, USA: Stanford University, 1998: 221-228.

[25] SCHOTT J R. Fault tolerant design using single and multi criteria genetic algorithm optimization[D]. Massachusetts: Cambridge University. Massachusetts Institute of Technology, 1995: 35-60.

(编辑  刘锦伟)

收稿日期：2015-09-16；修回日期：2015-11-05

基金项目(Foundation item)：辽宁省自然科学基金资助项目(2013020036) (Project(2013020036) supported by the Natural Science Foundation of Liaoning Province)

通信作者：戴永彬，博士，教授，从事非线性系统控制、过程控制研究；E-mail: dyb16@163.com