煤矿井下大功率开关电源的T-S模糊控制
胡俊达1, 2,言洁奕1,胡慧2
(1. 湘潭大学 信息工程学院,湖南 湘潭,411101;
2. 湖南工程学院 电气与信息工程系,湖南 湘潭,411101)
摘要:针对目前传统控制策略的不足,提出一种基于T-S模糊建模的煤矿井下大功率开关电源模糊控制方法。模型的前件参数由模糊C均值聚类算法确定,后件参数由带遗忘因子的最小二乘法辨识。通过对输出电压的实时检测采样,经过T-S模糊分析后输出控制量,调控占空比来改变IGBT通断时间,从而得到稳定的输出直流电压。采用MATLAB/Simulink仿真,验证了该方法的正确性和可行性。研究结果表明:与常规PI控制方法相比,T-S模糊控制策略在鲁棒性方面具有更好的控制效果。
关键词:大功率开关电源;T-S模糊模型;模糊C均值聚类;带遗忘因子的最小二乘法
中图分类号:TP273 文献标志码:A 文章编号:1672-7207(2013)05-1938-06
T-S fuzzy control of high-power switching power supply in underground coal mine
HU Junda1, 2, YAN Jieyi1, HU Hui2
(1. School of Information Engineering, Xiangtan University, Xiangtan 411101, China;
2. Department of Electrical and Information Engineering, Hunan Institute of Engineering, Xiangtan 411101, China)
Abstract: In view of the current inadequacy of traditional control strategy, a fuzzy control method of high-power switching power supply based on T-S fuzzy modeling in underground coal mine was proposed. In T-S fuzzy modeling method, antecedent parameters were obtained by fuzzy C-means clustering algorithm and consequent parameters were identified by least square with forget factor. The output voltage was sampled in real-time, the process of T-S fuzzy was analyzed and control variable was obtained, which was used to adjust the duty cycle to change IGBT on-off time, so as to acquire the stable output DC voltage. MATLAB/Simulink simulation was used to verify its correctness and feasibility. The results show that compared with conventional PI control method, the T-S fuzzy control strategy has good effect on the robustness.
Key words: high-power switching power supple; T-S fuzzy model; fuzzy C-means clustering; least square with forget factor
近年来,随着大功率全控型电力电子器件应用技术的不断成熟以及煤炭生产技术的不断发展,大功率采煤机组及运输设备不断应用,大大增加了对大功率开关电源的需求。然而,由于特殊的开采空间和煤层结构使得煤矿井下环境十分恶劣,致使供电网络结构复杂,供电负荷种类繁多,因此,对大功率开关电源的性能提出了更高的要求。煤炭是我国重要能源,国家对煤矿安全高度重视,全国煤矿特别是高瓦斯矿井和煤与瓦斯突出矿井必须依照2010版《煤矿安全规程》和MT/T 408—1995(《煤矿用直流稳压电源》)的规定来设计直流电源。在环境恶劣的井下,直流电源有以下特殊要求:一是需要隔爆兼本质安全型输出;二是可靠性高;三是电网适应性强;四是抗干扰性强;五是安装方便;六是能不间断供电。而开关型稳压电源具有的效率高、温升小、适应性强、体积小、密度小的特点使其成为矿井电源发展的主要方向。目前,PWM方式的单闭环控制、双闭环控制以及常规PI和PID控制在煤矿用开关电源中得到广泛应用,然而,由于矿用电源对性能要求比较苛刻,模型相对复杂,因而采用传统控制策略已经无法很好地满足要求[1-2]。随着计算机技术和控制理论的不断发展,实现煤矿用大功率开关电源的数字化和智能化控制已成为发展的必然趋势。近年来,由于模糊控制附加成本不高但可获得精确的控制效果,因而得到广泛应用。而Takagi-Sugeno(T-S)模糊控制作为一种新颖的控制方法,正引起学者们的关注[3-13]。它作为模糊控制中解决非线性问题的一种有效方法,具有结构简单、逼近能力强等特点,以局部线性化为基础,通过模糊推理方法实现全局的非线性,使得模型的全局输出具有良好的数学表达特性。因此,将T-S模糊控制应用于煤矿用大功率开关电源中,能够广泛地对非线性系统动态特性进行描述和表达,以提高系统的性能,使系统输出迅速地达到或接近预先设定值。
1 电路结构
开关电源是由功率变换电路和控制电路2部分组成。原理框图如图1所示。
大功率开关电源的主电路采用“AC—DC—AC—DC”变换的拓扑结构,由三相桥式二极管整流滤波电路,将交流电变为直流电,又经桥式逆变电路将直流电变为频率较高的交流方波,高频交流方波经高频脉冲变压器耦合到次级,通过高频二次整流滤波后输出所需直流电压。
控制电路是在输入电压、内部参数、外部负载发生变化时,来调节功率开关器件的导通时间,使得开关电源的输出电压保持恒定。所以,在开关电源的设计中,控制方法的选择和设计对开关电源的性能十分重要。
1.1 移相全桥ZVZCS变换器的小信号模型
DC-DC变换器是构建大功率开关电源的核心部分,因而,在Buck变换器PWM开关等效模型的基础上,引入副边电压有效占空比的概念,结合FB-ZVZCS-PWM开关变换器的特性,从小信号动态分析角度建立FB-ZVZCS-PWM开关变换器的等效电路模型。
FB-ZVZCS-PWM 变换器的拓扑结构如图2所示,其中:S1~S4为功率开关器件IGBT模块;S1和S3称为超前臂;S2和S4称为滞后臂;且S1和S3分别超前S2和S4相位角θ;D1~D4为器件自带的反并联二极管;C1和C2分别为S1和S2的并联电容;Lk为变压器回路的等效漏感;变压器原副边匝比为n;D5~D8为输出整流二极管;Cs为辅助电容;Lf为输出电感;Cf为输出电容;R为负载。
通过对变换器工作过程的分析,经过计算可得变压器副边电压的有效占空比deff的数学表达式,再对其施加小信号扰动,并忽略高阶项,可得:
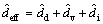 (1)
(1)
式中: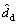 ,
,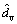 和
和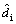 分别表示原边占空比扰动、输入电压扰动和输出电流扰动。通过对比Buck变换器得到FB-ZVZCS-PWM 变换器小信号模型,如图3所示。
分别表示原边占空比扰动、输入电压扰动和输出电流扰动。通过对比Buck变换器得到FB-ZVZCS-PWM 变换器小信号模型,如图3所示。
令输入扰动为0,且假设Rd远远小于R时可忽略Rd/R,同时Gd(s)≈1,则移相全桥变换器的控制-输出传递函数Gvd(s)为
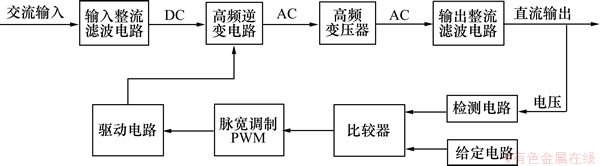
图1 开关电源的原理框图
Fig.1 Principle scheme of switching power supply
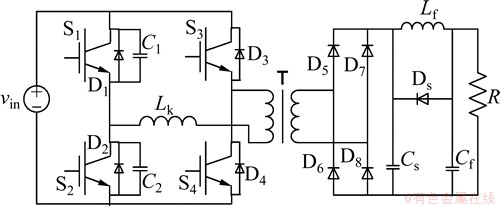
图2 FB-ZVZCS-PWM 变换器的拓扑结构
Fig.2 Topology of FB-ZVZCS-PWM converter
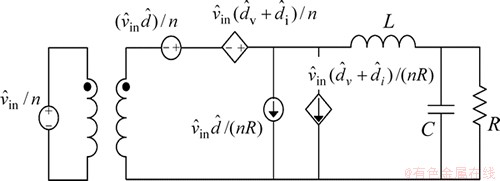
图3 FB-ZVZCS-PWM 变换器小信号模型
Fig.3 Small signal model of FB-ZVZCS-PWM converter
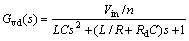 (2)
(2)
其中:Rd为负载电流引起的原边电压损失与负载电流的比值。变换器的具体工作过程分析和小信号模型的建立见文献[14]。
1.2 控制电路
开关电源作为一个闭环的自动控制系统,其控制环节是设计的重要组成部分,控制电路部分实际上是一个实时检测和控制系统。通过修改PWM波占空比改变逆变桥中IGBT的通断时间从而控制输出电压。T-S模糊控制系统为两输入单输出结构,输入为电压误差Ue和电压误差变化率Uec,输出为控制量V。T-S模糊控制系统结构如图4所示。

图4 T-S模糊控制系统结构图
Fig.4 Frame of T-S fuzzy control system
2 控制策略
对于T-S模糊模型,由于其规则前件是模糊变量形式,而结论部分是输入输出线性函数的表达式,因此,将其规则前件和结论后件分开来辨识。对于T-S模糊模型的前提部分参数,采用基于线性原型的模糊C-均值算法对其辨识,得到各模糊规则变量即规则数和隶属度函数的中心点;对于T-S模糊模型的后件参数即结论参数,由带遗忘因子的最小二乘法来辨识。
2.1 T-S模糊模型
T-S模型可以用n条模糊规则组成的集合来表示,则可得到如下一般模型[15]:
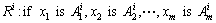 ,
,
then 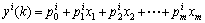 ;
;
i=1, 2, …, m (3)
根据电路的特点及控制要求,设T-S模糊控制器为两输入和单输出,则有
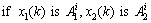 ,
,
then 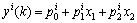 ; i=1, 2, …, n (4)
; i=1, 2, …, n (4)
式中:x1(k)和x2(k)分别记为k时刻电压误差Ue和电压误差变化率Uec;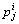 为第i条模糊规则的结论表达式中第j个参数;j=1, 2, …, m;yi为第i条规则输出控制量V。采用高斯型隶属函数,即
为第i条模糊规则的结论表达式中第j个参数;j=1, 2, …, m;yi为第i条规则输出控制量V。采用高斯型隶属函数,即
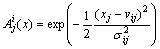 (5)
(5)
其中:vij和σij分别为各规则空间的中心和方差,它们都是待辨识的前件参数。T-S模糊模型在k时刻的被控系统的总输出由式(5)中的yi (i=1, 2, …, n)加权平均求得:
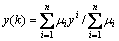 (6)
(6)
其中:n为模糊规则数;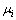 为广义输入向量的第i条规则的隶属度,
为广义输入向量的第i条规则的隶属度,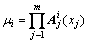 ;
;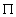 为模糊算子,通常取极小或乘积运算。
为模糊算子,通常取极小或乘积运算。
2.2 规则前件的辨识
采用基于线性聚类原型的模糊C-均值算法辨识模糊模型前件结构及参数。运用自适应距离测度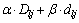 。式中:
。式中: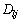 为数据xj (j=1, 2, …, n)到线性聚类原型pi (i=1, 2, …, c)的距离;dlj为数据xj到聚类中心θi (i=1, 2, …, c)的距离;
为数据xj (j=1, 2, …, n)到线性聚类原型pi (i=1, 2, …, c)的距离;dlj为数据xj到聚类中心θi (i=1, 2, …, c)的距离;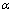 和
和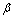 为参数。算法的目标函数为
为参数。算法的目标函数为
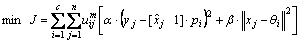
模糊C-均值算法步骤如下。
设有n个样本组成的样本集为{x1, x2, …, xn},则令
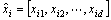 ,
,
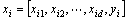 ;i=1, 2, …, n。
;i=1, 2, …, n。
(1) 给定聚类类别数c,2≤c≤n(其中n为数据个数),设定迭代终止阈值ε,初始化G(0),令迭代计数器L=0。
(2) 使用式(7)求聚类中心,使用式(8)求线性聚类原型。
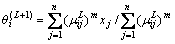 (7)
(7)
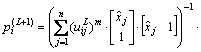
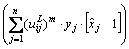 (8)
(8)
(3) 利用式(9)求数据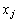 (j=1, 2, …, n)到线性聚类原型
(j=1, 2, …, n)到线性聚类原型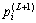 (i=1, 2, …, c)的距离
(i=1, 2, …, c)的距离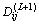 ,利用式(8)求
,利用式(8)求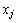 到聚类中心
到聚类中心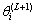 (i=1, 2, …, c)的距离
(i=1, 2, …, c)的距离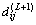 ;然后,将
;然后,将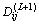 和
和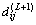 利用式(9)更新
利用式(9)更新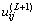 :
:
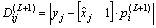 (9)
(9)
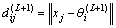 (10)
(10)
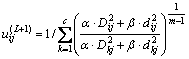 (11)
(11)
(4) 若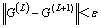 ,则终止;否则,令L=L+1,返回步骤(2)。
,则终止;否则,令L=L+1,返回步骤(2)。
2.3 结论参数的辨识
最小二乘向量形式的T-S模型:
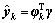 (12)
(12)
其中: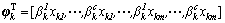 ;
;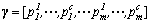 。
。
可利用带遗忘因子的递推最小二乘法来辨识模型后件参数,则有:
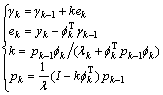 (13)
(13)
为了更好地保持辨识的动态性,则遗忘因子不取固定值,而是根据模型误差来计算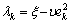 。其中:
。其中:
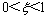 ,
,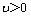 ;且
;且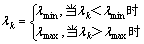
通过上面的描述,可以得到基于聚类算法的模糊建模步骤如下:
(1) 利用改进的基于线性聚类原型的模糊C-均值算法进行离线辨识得到模糊前件参数。
(2)对k时刻输入数据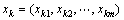 计算
计算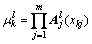 ,
,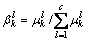 ,
,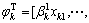
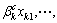
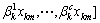 。
。
(3) 利用式(12)辨识参数。
(4) 令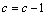 ,转到步骤(2),否则利用式(6)计算系统输出。
,转到步骤(2),否则利用式(6)计算系统输出。
3 系统仿真
针对T-S模糊控制算法,利用MATLAB仿真软件进行仿真实验,并与常规PI控制仿真结果进行比较。仿真中的主要参数如下:交流输入电压Uin=380 V,电压频率为50 Hz。设定直流输出电压为120 V,输入电感Li=3.6 mH,输入电容Ci=1 290 μF,输出电感Lf=64 μH,输出电容Cf=2 200 μF,变压比n:1=3:1,漏感Lk=8 μH,负载电阻RL=100Ω,t=0~1 s。当对系统施加阶跃噪声扰动时,不同控制下的输出电压波形见图5和图6。
当系统的负载发生变化时(当t=0.4 s时,RL=180Ω;当t=0.8 s时,RL=30Ω),输出电压波形如图7和图8所示;当系统的输入电压发生变化时(当t=0.4 s时,Uin=450 V;当t=0.4 s时,Uin=260 V),输出电压波形如图9和图10所示。
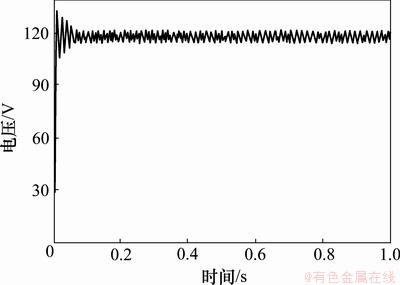
图5 在PI控制下施加阶跃噪声时的输出电压波形
Fig.5 Output voltage waveform under PI control when adding step noise
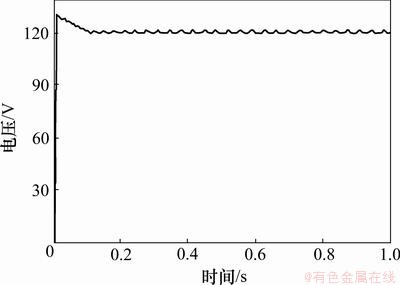
图6 在T-S模糊控制下施加阶跃噪声时的输出电压波形
Fig.6 Output voltage waveform under T-S fuzzy control when adding step noise
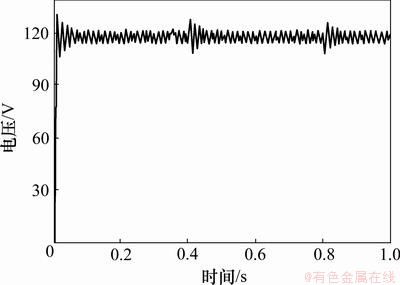
图7 在PI控制下负载变化时的输出电压波形
Fig.7 Output voltage waveform under PI control when load changes suddenly
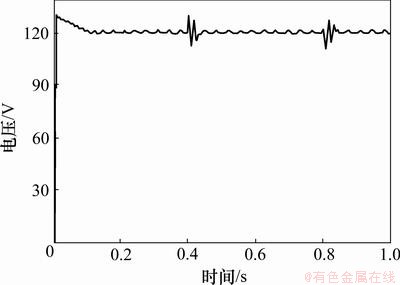
图8 在T-S模糊控制下负载变化时的输出电压波形
Fig.8 Output voltage waveform under TS fuzzy control when load changes suddenly
图5、图7和图9的输出电压偏离稳态值120 V的偏离范围分别大于图6、图8和图10中的输出电压偏离稳态值120 V的偏离范围。
从仿真结果可以得知:在阶跃噪声扰动、负载和输入电压变化的情况下,与基于PI控制系统的动态响应性能相比,基于T-S模糊控制系统具有较好的鲁棒性。
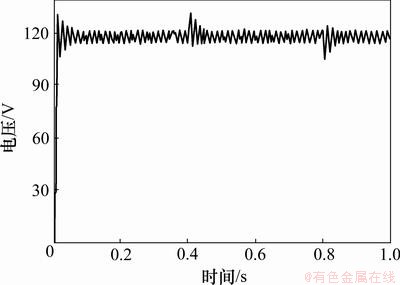
图9 在PI控制下输入电压变化时的输出电压波形
Fig.9 Output voltage waveform under PI control when input voltage changes suddenly
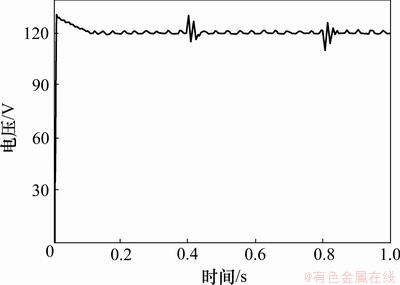
图10 在T-S模糊控制下输入电压变化时的输出电压波形
Fig.10 Output voltage waveform under T-S fuzzy control when input voltage changes suddenly
从仿真结果可以看出:在阶跃噪声扰动、负载和输入电压变化的情况下,与基于PI控制系统的动态响应性能相比较,基于T-S模糊控制系统的响应速度快,超调量较小,且过渡时间短,系统具有较好的鲁棒性。
4 结论
(1) 采用基于线性原型的模糊C-均值聚类和带遗忘因子的最小二乘法辨识的T-S模糊模型, 可实现对具有非线性特征的开关电源的精确建模。
(2) 与常规PI控制方法相比,采用T-S模糊控制可在复杂的矿井环境中获得更好的控制性能。
(3) 设计T-S模糊控制器,可为解决非线性系统特别是难以用传统方法求解的复杂非线性系统控制问题提供一种有效途径。
参考文献:
[1] 成庶, 陈特放, 余明扬. 开关电源时变模型的新型PID算法[J]. 中南大学学报: 自然科学版, 2007, 38(5): 970-974.
CHENG Shu, CHEN Tefang, YU Mingyang. A novel PID algorithm for timer-variable model of switching mode power supply[J]. Journal of Central South University: Science and Technology, 2007, 38(5): 970-974.
[2] 徐应年, 赵阳, 谌海涛, 等. 电压型逆变电源输出电压IMC-PID控制技术研究[J]. 中国电机工程学报, 2007, 27(28): 90-95.
XU Yingnian, ZHAO Yang, CHEN Haitao, et al. Research on waveform control technique based on IMC-PID for voltage- source inverter[J]. Proceedings of the CSEE, 2007, 27(28): 90-95.
[3] 熊浩, 陈伟根, 杜林, 等. 基于T-S模型的电力变压器顶层油温预测研究[J]. 中国电机工程学报, 2007, 27(30): 15-19.
XIONG Hao, CHEN Weigen, DU Lin, et al. Study on prediction of top-oil temperature for power transformer based on T-S model[J]. Proceedings of the CSEE, 2007, 27(30): 15-19.
[4] Abdallah S, Zohra K, Naceur B B. On the state observer based stabilization of T-S systems with maximum convergence rate[J]. International Journal of Engineering, 2009, 3(3): 293-305.
[5] DONG Jiuxiang, YANG Guanghong. H∞ controller synthesis via switched PDC scheme for discrete-time T-S fuzzy systems[J]. IEEE Transactions on Fuzzy Systems, 2009, 17(3): 544-555.
[6] CHEN Peng, DONG Yue, TIAN Yuchu. New approach on robust delay-dependent H∞ control for uncertain T-S fuzzy systems with interval time-varying delay[J]. IEEE Transactions on Fuzzy Systems, 2009, 17(4): 890-900.
[7] HUA Changchun, WANG Qingguo, GUAN Xinping. Robust adaptive controller design for nonlinear time-delay systems via T-S fuzzy approach[J]. IEEE Transactions on Fuzzy Systems, 2009, 17(5): 1143-1156.
[8] CHEN Peng, DONG Yue, YANG Taicheng, et al. On delay-dependent approach for robust stability and stabilization of T-S fuzzy systems with constant delay and uncertainties[J]. IEEE Transactions on Fuzzy Systems, 2009, 17(5): 1143-1156.
[9] Chen S H, Ho W H, Chou J H. Robust controllability of T-S fuzzy-model-based control systems with parametric uncertainties[J]. IEEE Transactions on Fuzzy Systems, 2009, 17(6): 1324-1335.
[10] 刘剑锋, 刘友梅, 桂卫华, 等. 基于模糊预测控制的机车制动控制方法[J]. 中南大学学报: 自然科学版, 2009, 40(5): 1329-1335.
LIU Jianfeng, LIU Youmei, GUI Weihua, et al. Locomotive brake control method based on fuzzy predictive control[J]. Journal of Central South University: Science and Technology, 2009, 40(5): 1329-1335.
[11] ZHANG Xiaohong, Anmar K, DONG Li, et al. Impulsive stability of chaotic systems represented by T-S model[J]. Chaos, Solitons and Fractals, 2009, 41(4): 1-7.
[12] Hirosato S, Iroaki I, Masaharu M. On the monotonicity of fuzzy- inference methods related to T-S inference method[J]. IEEE Transactions on Fuzzy Systems, 2010, 18(3): 629-634.
[13] Hamdi G, Ahmed E H, Mohamed C. Robust control of T-S fuzzy systems with time-varying delay using new approach[J]. International Journal of Robust and Nonlinear Control, 2010, 20(14): 1565-1578.
[14] 陈特放, 付强, 陈春阳, 等. 一种新型移相控制FB-ZVZCS- PWM变换器[J]. 西南交通大学学报, 2010, 45(6): 843-849.
CHEN Tefang, FU Qiang, CHEN Chunyang, et al. Novel FB-ZVZCS-PWM converter based on phase-shift control[J]. Journal of Southwest Jiaotong University, 2010, 45(6): 843-849.
[15] 颜文旭, 纪志成. 三相有源电力滤波器的T-S模糊建模与控制[J]. 电机与控制学报, 2010, 14(11): 92-99.
YAN Wenxu, JI Zhicheng. T-S fuzzy model and control for three-phase shunt APF[J]. Electric Machines and Control, 2010, 14(11): 92-99.
(编辑 陈灿华)
收稿日期:2012-04-28;修回日期:2012-07-22
基金项目:国家自然科学基金资助项目(5177040);湖南省自然科学基金资助项目(09JJ3094);湖南省科技厅科技计划项目(2011FJ3126)
通信作者:胡俊达(1954-),男,湖南长沙人,教授,硕士生导师,从事电力电子技术与智能控制研究;电话:15367100268;E-mail: hjd112233@126.com