Thermodynamic optimization of Mg-Nd system

MENG Fan-gui(孟凡桂), LIU Hua-shan(刘华山), LIU Li-bin(刘立斌), JIN Zhan-peng(金展鹏)

School of Materials Science and Engineering, Central South University, Changsha 410083, China

Received 15 September 2005; accepted 28 March 2006

Abstract: Based on the reported experimental data, the phase diagram of Mg-Nd binary system was optimized using the CALPHAD approach. Gibbs energies of the disordered BCC_A2 and ordered BCC_B2 phases were modeled with a single expression based on a 2-sublattice model. Liquid and terminal solutions, such as dHCP and HCP, were modeled as substitutional solutions. Intermediate phases Mg₂Nd, Mg₃Nd and Mg₄₁Nd₅ were treated as stoichiometric compounds. The optimization was carried out in the Thermo-Calc package. A set of thermodynamic parameters is obtained. Calculated phase diagram, enthalpies of formation and Gibbs energies of formation are in reasonable agreement with the experimental data.

Key words: Mg; Nd; optimization; phase diagram

1 Introduction

Magnesium alloys have attracted many attentions in recent years due to their low density, high specific strength, and good castability, etc. Rare earths, as an important class of alloying elements to magnesium-based alloys, are recently often added into Mg matrix to enhance the high temperature properties and casting characteristics of the alloys[1].

However, the mechanism why the rare earths can improve the performances of the magnesium-based alloys has not been clearly identified. Phase relations in temperature-composition space of the Mg-related systems are particularly helpful to comprehend the interaction between different elements and promote the development of new Mg-based materials with superior properties. The present work aims at the development of a consistent thermodynamic description of the Mg-Nd binary system using the CALPHAD technique. The Mg-Nd phase diagram was formerly optimized and calculated by GORSSE et al[2] using substitutional solution and associate models for the liquid phase. The optimized results showed that the substitutional solution model did not describe the phase equilibria well in the Mg-Nd system. Better agreement was obtained by using the associate model. But the homogeneity range of MgNd (BCC_B2) and the order-disorder transformation between BCC_A2 and BCC_B2 phase were not taken into account. In view of these, thermodynamic reassessment of the Mg-Nd system was performed in the present work.

  2 Experimental

2.1 Phase diagram data

The Mg-Nd phase diagram was first constructed by NAYEB-HASHEMI and CLARK[3] according to reported data[4-7] and the assumed similarities to Mg-La, Mg-Ce, and Mg-Pr. It is believed that there are liquid, the terminal solid solutions of HCP (Mg), dHCP (Nd) and BCC_A2 (Mg) along with five intermetallic compounds, Mg₁₂Nd, Mg₄₁Nd₅, Mg₃Nd, Mg₂Nd, and MgNd in this system. According to NAYEB-HASHEMI and CLARK[3], the Mg-rich eutectic temperature was  at (821±2) K. The maximum solid solubility of Mg in dHCP (Nd) was determined by JOSEPH and GSCHNEIDNER[4] to be at 8.2%Mg (mole fraction) at the eutectoid decomposition temperature of BCC_A2 (824 K). The solid solubility of Nd in HCP(Mg) was measured by PARK and WYMAN[5], ROKHLIN[6], DRITS et al[7]. There are obvious discrepancies among these experimental results [5-7]. Because the higher- purity materials and the more reliable method were used, the value (0.10% Nd at 819 K) measured by PARK and WYMAN[5] should be more reliable. Thus the solid solubility of 0.10% Nd in HCP(Mg) is accepted in the present optimization.

A systematic investigation of the Mg-Nd phase diagram was performed by DELFINO et al[8] using DTA, X-ray diffraction, metallography, and microprobe analysis. They determined the liquidus in the whole composition range, part of solvus and solidus, and temperature of all invariant equilibria by DTA; moreover, they checked the reaction type of most invariant equilibria by optical or SEM micrographs. The Mg-rich eutectic temperature, the eutectoid decomposition temperature of BCC_A2 and the maximum solid solubility of Mg in dHCP show good agreement with the recommended values by NAYEB-HASHEMI and CLARK[3]. For the Mg₂Nd phase, a peritectic formation was assumed at a temperature slightly higher than 1 023 K, the temperature for the eutectic reaction, liquid→ MgNd(BCC_B2)+Mg₂Nd. In addition, DELFINO et al[8] found that Mg₁₂Nd phase is metastable because it only exists in the samples quenched from the liquid state. Homogeneity ranges of all compounds in this system were not determined[8]. However, according to Ref.[8], thermal effects were observed for the 44.0%Mg (molar fraction) and 47.5%Mg (molar fraction) alloys at about 818 K, the eutectoid decomposition temperature of BCC_A2. Therefore, the content of Mg in MgNd seems to be higher than 47.5% Mg. But in fact these thermal effects were observed from DTA of cooling process. During this process, nonequilibrium solidification is very likely to occur. So the opinion that the content of Mg in MgNd compound can not be lower than 47.5% Mg may not be accepted.

Recently, XU et al[9] studied the Mg-Nd diffusion couple annealed at 773 K for 100 h by X-ray energy dispersive spectroscopy with a back-scattered scanning electron microscopy. It was found that MgNd has a homogeneity range of about 40% to 50% Mg and Mg₃Nd is nearly a stoichiometric compound.

Homogeneity ranges of other compounds were not measured. Hence, only the composition range of MgNd is taken into account and other compounds are considered to be stoichiometric ones.

2.2 Thermodynamic data

With the Knudsen effusion method, PAHLMAN and SMITH[10] measured the vapor pressures of magnesium over Mg-Nd alloys, and derived the enthalpy and Gibbs energies of formation of the intermediate phases from the pure solid elements at 773 K. The enthalpy of formation of MgNd from pure solid Mg and Nd was also determined by OGREN et al[11] with the vapor pressure method. Two groups of results agree well with each other. OUYANG et al[12] calculated the enthalpy of formation of all intermediate compounds in this system with Miedema theory. But these calculated data show considerable discrepancies with the experimental data in the Mg-rich side. Because of the simple treatment of the Miedema theory, these data were only introduced to compare with the optimized values.

The thermodynamic properties of liquid Mg-Nd alloys were not published in the literature.

3 Thermodynamic modeling

The thermodynamic models adopted here are summarized in Table 1 and briefly introduced in the following.

Table 1 Summary of thermodynamic models adopted

  3.1 Solution phases: liquid, HCP(Mg), dHCP(α-Nd) and BCC_A2

The Gibbs energies of solution phases, liquid, BCC_A2, HCP and dHCP, were described with a substitutional solution model based on random mixing of the metallic atoms. They are expressed as

(1)

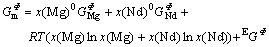
where 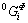  is the molar Gibbs energies of pure element of Φ phase; and are cited from the work of DINSDALE[13], except that  and 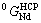 are taken from Ref.[14].

 is the excess Gibbs energy, formulated with the Redlich-Kister polynomial:

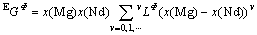       (2)

where  (v=0, 1, ???) are the interaction parameters between elements Mg and Nd.

The general form for  is

                                         (3)

where   and  are parameters resulting from an optimization process.

  3.2 BCC­­_A2 and BCC_B2 Phase

The Gibbs energies of the BCC_A2 and BCC_B2 were modeled with a single function [15] based on a two sublattice model (Mg,Nd)_0.5(Mg,Nd)_0.5:

      (4)

where  x_i represents the alloy mole fraction of constituent i;  and  are the so-called site fractions, i.e. the mole fractions in the first and second sublattices, respectively; the first term, , represents the Gibbs energy of the disordered phase BCC_A2 and is expressed by Eqn.(1); the second term, 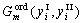, is the Gibbs energy of the ordered phase BCC_B2 as described by the sublattice model and contains implicitly a contribution of the disordered state, expressed as

(5)

The parameters ^vL have the form shown in Eqn.(3). Due to the crystallographical symmetry, the following relations are introduced in Ref.[15]:

                                                    (6)

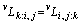                                       (7)

The last term in Eqn.(4), 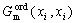, represents the energy contribution of the disordered state to the ordered phase. The last two terms cancel each other when the site fractions are equal, thus corresponding to a disordered phase. Hence, the parameters of both ordered and disordered phases can be evaluated independently.

3.3 Stoichiometric phases

Because there is no report on the homogeneity ranges of Mg₄₁Nd₅, Mg₃Nd and Mg₂Nd, they are treated as stoichiometric compounds, of which Gibbs energies are formulated with the following expression:

            (8)

where  a and b are the mole fraction of Mg and Nd in the compound, respectively; D and E are the parameters to be assessed.

4 Results and discussion

The Mg-Nd binary system was optimized in the PARROT module in Thermo-Calc software[16] based on the experimental data of phase diagram and thermodynamic properties. Reasonable agreement between the calculated results and experimental values is obtained.

Thermodynamic parameters optimized are listed in Table 2. The calculated phase diagram is shown in Fig.1. The invariant equilibria in the Mg-Nd system are listed in Table 3. It is clear that the calculated equilibria in the Mg-Nd system are in good agreement with most experimental data. According to our calculation, the homogeneity range of MgNd phase at 773 K is about 42%-50% Mg, while the experimental value determined by X-ray energy dispersive spectroscopy (EDS)[9] is about 40%-50% Mg. Obviously, the calculated homogeneity range of MgNd can be accepted considering the precision of EDS results. Fig.1 shows that the 44.0%Mg (molar fraction) and 47.5%Mg (molar fraction) alloys at about 818 K are in MgNd single-phase region. This result is reasonable since two thermal effects for the 44.0%Mg and 47.5%Mg alloys at about 818 K observed on cooling may correspond to eutectoid decom- decomposition of BCC_A2 phase formed from the nonequilibrium solidification that is very likely to occur during cooling process.

Fig.1 Phase diagram of Mg-Nd system calculated by present work compared with experimental data from Refs.[8-9]: ● Thermal effects observed on heating and cooling; △ Thermal effects observed on heating;  Thermal effects observed on cooling; ◇ Diffusion couple

Table 2 Thermodynamic parameters in the Mg-Nd system

Table 3 Special points of Mg-Nd phase diagram

Fig.2 shows the comparison of the enthalpy of formation at 773 K with the data measured by PAHLMAN and SMITH[10], and OGREN et al[11] calculated with Miedema theory by OUYANG et al[12]. The calculated values agree well with PAHLMAN’s and SMITH’s[10] and OGREN’s et al[11] experimental data.

Fig.2 Calculated enthalpy of formation in Mg-Nd system compared with experimental data

The comparison of Gibbs energies of formation at 773 K between the calculated and experimental data is shown in Fig.3. The calculated results show that the phase with the greatest relative stability in the Mg-Nd system is Mg₃Nd. It is in agreement with PAHLMAN and SMITH[10]. The calculated Gibbs energies of formation of all the compounds are consistent with experimental values except for Mg₄₁Nd₅. By considering the experimental errors introduced by vapor pressure method, and the fact that the peritectic nature of formation of the Mg₄₁Nd₅ phase may result in the presence of a small amount of nonequilibrium phase in the prepared alloys, this discrepancy is accepted in order to fit the phase diagram data for the Mg₄₁Nd₅ phase better.

Fig.3 Calculated Gibbs energies of formation in Mg-Nd system compared with experimental data

5 Conclusions

1) On the basis of the reported experimental data, a self-consistent thermodynamic description is developed by thermo- dynamic modeling and optimization.

2) Extensive comparisons between the calculated and experimental data are presented. The present description gives a good account of most of the experimental data.

References

[1] MORDIKE B L, EBERT T, Magnesium properties-applications potential [J]. Mater Sci Eng A, 2001, A302: 37-45.

[2] GORSSE S, HUTCHINSON C R, CHEVALIER B, NIE J F. A thermodynamic assessment of the Mg-Nd binary system using random solution and associate models for the liquid phase [J]. J Alloys Compounds, 2005, 39: 253-262.

[3] NAYEB-HASHEMI A A, CLARK J B. The Mg-Nd system [J]. Bull Alloy Phase Diagrams, 1988, 9: 618-623.

[4] JOSEPH R R, GSCHNEIDNER K A. Solid solubility of magnesium in some lanthanide metals [J]. Trans AIME, 1965, 233: 2063-2069.

[5] PARK R R, WYMAN L L. Phase relationships in magnesium alloys [J]. WACD Tech Rep, 1957, 33: 57-504.

[6] ROKHLIN L L. Solid solubility of neodymium and cerium in solid state magnesium [J]. Russ Met Fuels, 1962(2): 98-100.

[7] DRITS M E, PADEZHNOVA E M, MIKLINA N V. The combined solubility of neodymium and zinc in solid magnesium [J]. Russ Metall, 1971(1): 143-146.

[8] DELFINO S, SACCONE A, FERRO R. Phase relationships in the neodymium-magnesium alloy system [J]. Metall Trans A, 1990, 21: 2109-2114.

[9] XU Y, CHUMBLEY L S, WEIGELT G A, LAABS F C. Analysis of interdiffusion of Dy, Nd, and Pr in Mg [J]. J Mater Res, 2001, 16(11): 3287-3292.

[10] PAHLMAN J F, SMITH J F. Thermodynamics of formation of compounds in the Ce-Mg, Nd-Mg, Gd-Mg, Dy-Mg, Er-Mg, and Lu-Mg binary systems in the temperature range 650 to 930 K [J]. Metall Trans, 1972, 3: 2423-2432.

[11] OGREN J R, MAGNANI N J, SMITH J F. Thermodynamics of formation of binary rare earth-magnesium phases with CsCl-type structure [J]. Trans Soc AIME, 1967, 239: 766-771.

[12] OUYANG Yi-fang, ZHANG Bang-wei, LIAO Shu-zhi, JIN Zhan-peng. The study of thermodynamic properties for rare earth-magnesium alloys [J]. Rare Metal Mater Eng, 1995, 24: 32-37. (in Chinese)

[13] DINSDALE A T. Thermochemical data of the elements [J]. CALPHAD, 1991, 15: 317-425.

[14] DINSDALE A T. Private Communication, 2005-01-28.

[15] DUPIN N, ANSARA I. On the sublattice formalism applied to the B2 phase [J]. Z Metallkd, 1999, 90: 76-84.

[16] HELANDER T, HOGLUND L, ANDERSON J O, SHI P F, SUNDMAN B, ANDERSON J O. Thermo-Calc & DICTRA, computational tools for materials science [J]. CALPHAD, 2002, 26(2): 273-312.

Corresponding author: JIN Zhan-peng; Tel: +86-731-8836209; E-mail: jin@mail.csu.edu.cn

(Edited by LI Xaing-qun)