J. Cent. South Univ. (2018) 25: 2677-2687

DOI: https://doi.org/10.1007/s11771-018-3945-y

Numerical study on cavitation in a globe control valve with different numbers of anti-cavitation trims

Hamidreza YAGHOUBI, Seyed Amir Hossein MADANI, Mansour ALIZADEH

Department of Mechanical Engineering, Iran University of Science and Technology, Tehran 16846-13114, Iran

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: Cavitation is a destructive phenomenon in control valves. In order to delay cavitation, a multi-series of perforated cylindrical plates, called trims, are used. Previously, the effects of orifice diameter and different types of trims have been investigated. In this study, by numerical analysis, a globe control valve was investigated by employing four different cases (without trim, with one trim, with two and three trims) and the impact of the number of these trims on the intensity, formation region and the initiation point of cavitation was analyzed. It was found that the addition of one stage or two stages of trims reduces the intensity and delays the onset of cavitation, relative to the valve without trim. However, no significant differences in terms of intensity and initiation point of cavitation were observed in the cases where two or three trims were used. Therefore, due to the high cost of producing the trims, and the severe drop in flow coefficient, it is not economically and technically justified to increase the number of trims to more than three.

Key words: numerical analysis; anti-cavitation trim; globe control valve

Cite this article as: Hamidreza YAGHOUBI, Seyed Amir Hossein MADANI, Mansour ALIZADEH. Numerical study on cavitation in a globe control valve with different numbers of anti-cavitation trims [J]. Journal of Central South University, 2018, 25(11): 2677–2687. DOI: https://doi.org/10.1007/s11771-018-3945-y.

1 Introduction

Control valves are important components of the control process in industrial control systems. Control valves consist of two main parts: the valve body, which conveys and directs the flow; and the actuator, which provides the necessary force for the movement of valve components. The rate of flow passing through the globe valve is changed by adjusting the distance between a stationary seat and a movable plug.

Cavitation is one of the limiting parameters in the design and fabrication of globe control valves. This phenomenon occurs when the local pressure of the fluid becomes less than its saturation vapor pressure at the working temperature. Under these conditions, bubbles form in the low-pressure regions, are carried with the flow and collapse in the high-pressure regions, causing surface erosion and pitting of the metal [1]. The erosion rate changes with the upstream and downstream pressure difference, material used for body manufacturing and amount of oxygen dissolved in the water. From 0.1 to 5 g mass loss was reported after 20 h operation of a needle-valve, highlighting the importance of cavitation prevention [2, 3]. In order to eliminate the cavitation phenomenon or to reduce its intensity, a series of perforated cylindrical plates called trims are installed around the plug. These trims cause a multi-stage pressure drop in the flow and prevent the sudden drop of the fluid pressure to a lower point than its saturation vapor pressure. Therefore, the onset of cavitation is delayed, and at high flow rates the occurrence of cavitation is unavoidable, the intensity and the extent of the cavitation are reduced.

By making the control valves of Plexiglas, one can observe where the cavitation forms; however, this method is costly and cannot be used for all situations. DAVIS et al [4] installed a Plexiglas window in the casing of a valve and by injecting tracing particles and measuring the pressure and flow rate showed that the results obtained from numerical analysis have a good agreement with the experimental results. By building the control valve of Plexiglas, CHERN et al [5] observed the flow pattern and the vortices produced by the valve, and compared their findings with the analytical results. Also, experimental studies have been made investigating flow patterns in perforated plates. MAYNES et al [6] experimentally explored the flow passing through perforated plates and discovered the high dependency of the loss coefficient and cavitation numbers to plate geometry. AMIRANTE et al [7] experimentally and numerically investigated the effects of cavitation phenomena on the performance curves of a hydraulic proportional directional valve and estimated its influence on flow rate and flow coefficient as well.

As the bubbles collapse in high-pressure regions, noise and vibration are produced in the system. DINA [8] used the cavitation-induced noise to detect the onset of cavitation in centrifugal pumps. MARTIN et al [9] stated that high- frequency response pressure transducers are useful tools for diagnosing cavitation inception correlating noise with the cavitation index.

Because of the high cost of empirical methods, the use of computational fluid dynamics for the analysis of flow and cavitation phenomenon in control valves is on the rise. By numerically solving the flow in a poppet valve, HONG et al [10] investigated the effects of parameters such as outlet pressure, inlet velocity and valve stem travel on the cavitation formation region and the maximum vapor volume fraction. They found that, with the increase in the inlet flow rate, the maximum vapor volume fraction increases, and this increase is enormous at the onset of cavitation. AN et al [11] analyzed the globe anti-cavitation valves which are in marine LNG systems. They investigated the effects of the orifice diameter of the trim and the size of the valve discharge on the flow pattern and cavitation intensity. The cavitation intensity in the newly designed valves was less than that in the conventional control valves, and the flow pattern had improved. Through experimental investigations of the globe control valve, RAMMOHAN et al [12] studied the impact of five different types of cages with different numbers and types of perforations on the flow capacity and cavitation. They discovered that, by increasing the number of cage perforations, cavitation intensity diminishes and the onset of cavitation is postponed, while flow capacity drops. Based on input-output linearization, MU et al [13] proved that a nonlinear mathematical model of the flapper nozzle servo valve was a highly advantageous model and the results included useful methods for high-precision position tracking of electro hydraulic servo valves. CHERN et al [14] used numerical analysis to compare a one-stage step cage valve and a one-stage perforated cage valve with a valve without a cage. The cavitation intensity in the valves with cages, at different valve stem travels, was less than that in the valve without a cage. JIN et al [15] investigated the flow field in a pressure reducing valve with an orifice plate. They conducted a numerical study trying to optimize the valve’s body and the orifice’s structure in order to determine the decline of energy loss. AMIRANTE et al [16] employed a full three-dimensional model of the flow field to optimize the design of the sliding spool of a hydraulic proportional valve and reduce the opening force exerted by the solenoid actuator. As a result, the operating zone of the valve became larger due to the decline in the flow force acting on the spool. AUNG et al [17] used numerical analysis to research the cavitation phenomenon in the flapper-nozzle pilot stage of an electrohydraulic servo-valve. They compared two different types of flappers: innovative and traditional flappers. Cavitation was reduced considerably more around the surfaces of the innovative flapper compared to the traditional flapper, and the transverse force, which is an undesirable force, was eliminated in the innovative flapper.

Today, most of the globe control valves used in the industry have trims. In previous studies, the effects of the orifice diameter and trim type on the cavitation intensity and flow pattern have been investigated [11, 14]. In the present study, using the FLUENT 6.3 commercial software, the globe control valve was analyzed in four different cases (no-trim, one trim, two and three trims), and the effect of the trims on the initiation point, location and intensity of cavitation, velocity field and pressure distribution were determined. By adding one and two stages of trims, the cavitation intensity was reduced considerably relative to the valve without trim and the occurrence of cavitation was delayed. By adding more trims, this trend was expected to continue; but the investigations showed that there is no much difference between two and three trims’ cases in terms of the cavitation intensity, region of cavitation formation and the cavitation onset flow rate, due to the high cost of economically justifiable.

2 Subject of study

As a case study, a conventional DN 50 globe valve was chosen for analysis (Figure 1). We appreciate the fact that any changes in either valve geometry or its size can have an impact on the hydraulic calculations and results. Similar results should be expected to be observed for valves different from this case in size and geometry. However, for further clarifications, analysis of the same valve type with different sizes and geometries is suggested as a future work. The geometry of this valve has been adopted from an industrial model without trims. Since the trims occupy a large space, in order to install them, the upper section of a traditional valve’s body is modified so that fluid could easily flow around the most outer trim. The plug curve is an important parameter in globe valves because this curve represents the flow characteristics of the valve. When the plug moves away from the seat, the cross section area of fluid flow gets bigger and the flow rate increases. The plug of a traditional valve initially has quick- opening inherent flow characteristics; and by modifying the valve, it changes to linear inherent flow characteristics (Figure 2).

The linear plug curve is expressed by Eq. (1):

y=0.000002x⁶–0.0001x⁵+0.0026x⁴–0.0263x³+0.1365x²–0.1921x+0.0039, 0 mm (1)

2.1 Grid model

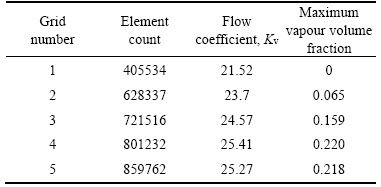
The first step in numerical analysis is to generate a geometric model for the flow path. Due to the symmetry of the geometry and boundary conditions, only half of the geometry was analyzed, which reduced the computation time. The computational domain included the fluid enclosure of the body, 10 pipe-diameters of upstream pipe, and 20 pipe-diameters of downstream pipe. The unstructured grid consists of tetrahedral elements with five prismatic layers along all the walls. The prismatic elements were used to resolve the near-wall boundary region. Mesh density is higher at the lower section of the plug, near the seat and around the orifices. It should be mentioned that more cells are generated with the reduction in the diameter of the orifices and increases in the number of trims. To evaluate the independency of the results from the number of mesh elements, the flow coefficient and the maximum vapor volume fraction in the entire domain have been investigated. Table 1 shows the independency of the results from the mesh elements, which accordingly, the average number of elements has been considered 850000. An example of a mesh grid generated for analysis is shown in Figure 3.

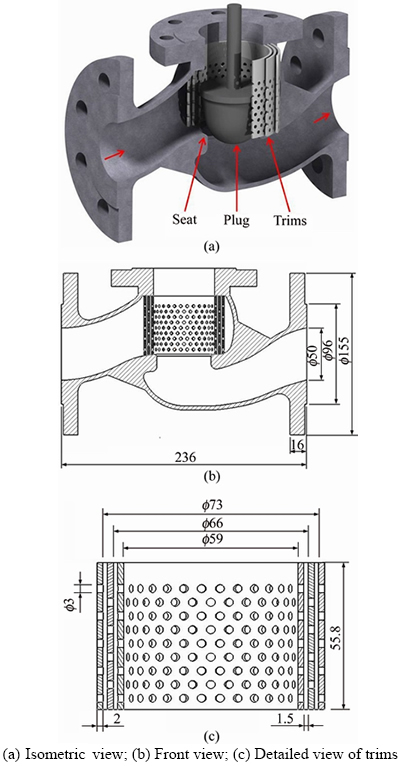
Figure 1 DN 50 control valve (Unit: mm):

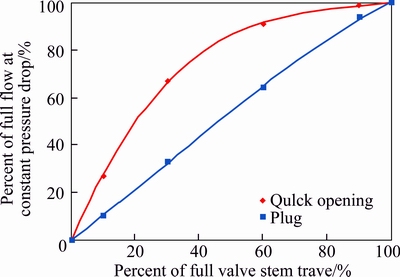
Figure 2 Inherent flow characteristics curves

Table 1 Grid independency test of various meshes

2.2 Mathematical formulation

Since the fluid passing through the valve contains a mixture of water and vapor phases, the numerical simulation has been performed using the mixture model. The mass and momentum conservation law must hold for the passing fluid. Thus, the main governing equations in this study are the continuity and the Navier-Stokes equations. The second order discretization was used to obtain more accurate results for all the computational calculus. Since the flow’s Reynolds number is higher than 2300, turbulence behavior is exhibited by the fluid [18], and the turbulence model is needed to solve the relevant equations. For this purpose, using the Reynolds average method, the mean values of the physical variables are substituted into the following equations:

Continuity equation:

                      (2)

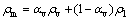                      (3)

In the above equations,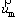is the mass- averaged velocity; ρ_m is the density of the mixture; ρ_l and ρ_v are the densities of water and vapor, respectively; α_v is the volume fraction of vapor.

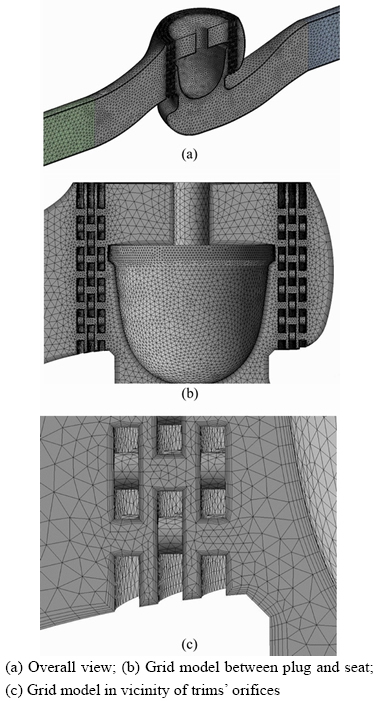
Figure 3 Computational grid of control valve:

Momentum transfer equation:

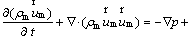
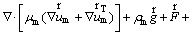
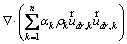                   (4)

where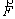is the body force; n is the number of phases;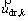is the velocity drift of the secondary phase; 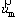is the mass-averaged velocity and μ_m is the mixture viscosity [19].

For solving the Reynolds average Navier- Stokes equations, since the previous studies have obtained good results by using the standard k–ε model (MAHMOUD et al [20]; MARGOT et al [21]; SINGHAL et al [22]), this model was employed to simulate the turbulent flow. In this model, the turbulent kinetic energy (k) and the dissipation rate (ε) are written in the form of the following two transport equations:

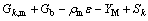                (5)

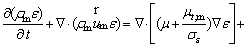
       (6)

et al.mixture viscosity [18

where G_k is the turbulent kinetic energy due to the velocity gradients and G_b is the kinetic energy due to buoyancy; Y_m represents the contribution of the fluctuating dilatation in compressible turbulence to the overall dissipation rate; C_1ε, C_2ε, C_3ε are constant numbers; σ_k and σ_ε are the turbulent Prandtl numbers for k and ε respectively; S_k and S_E are user-defined terms; μ_t is the turbulent viscosity, which is determined from the following equation:

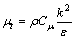                             (7)

The model constants have the following default values [23]:

C_1ε=1.44, C_2ε=1.92, C_3ε=1, C_μ=0.09, σ_k=1.0, σ_ε=1.36

The cavitation model of this scheme is based on the full cavitation model [22] in which the effect of non-condensable gases is considered. To show the interactions between the liquid and vapor phases in this cavitation model, the following vapor mass fraction equation (vapor transport equation) is used:

   (8)

where γ is the effective exchange coefficient and f_v is the vapor mass fraction; R_eva and R_cond indicate the evaporation rate (vapor generation) and the condensation rate (vapor conversion to liquid), whose equations for a complete cavitation model are obtained from the Rayleigh-Plesset equations, as follows.

In the state of evaporation, the pressure becomes less than the saturation pressure (p≤p_sat), so we have:

       (9)

where f_g is the mass fraction of gases. In the state of condensation, the pressure becomes greater than the saturation pressure (p≥p_sat), so we have:

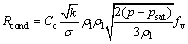            (10)

where C_e and C_c are proper coefficients for the evaporation and condensation rates, respectively. SINGHAL et al [22] have determined the values of these coefficients as C_e=0.02 and C_c=0.01. In addition to the reduction of the fluid’s local pressure below the vapor pressure, experience has shown that turbulent changes of pressure in the jets and the wakes created in the fluid medium constitute the other factors that lead to cavitation [24]. Therefore, to consider this turbulent phenomenon in the cavitation model being used, the saturation vapor pressure is assumed a little higher than the local saturation pressure at that point. In other words, local pressure announces the emergence of cavitation at pressures a little higher than the saturation vapor pressure.

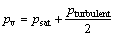                      (11)

In the above relationship, p_v is the saturation vapor pressure; p_sat is the local saturation pressure; the turbulent pressure fluctuation is p_turbulent= 0.39k [25].

2.3 Boundary conditions

In this study, the inlet velocity boundary condition has been generally used; and in certain cases, the inlet pressure boundary condition has been applied for comparing the pressure distribution. The inlet velocity profile was defined using the 1/7th power-law profile given by Eq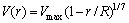. (12):

                    (12)

where V(r) is the axial velocity; V_max is the maximum velocity at the center of tube; r is the radial coordinate and R is the tube radius. At the outlet, the pressure outlet boundary condition has been applied. The outlet pressure is 2.0×10³ kPa (absolute), and it is constant for all the performed analysis. The inlet turbulence intensity was calculated by Eq. (13) for all simulations [19] under conditions that the hydraulic diameter is 50 mm, the considered fluid is water, the vaporization pressure is 3540 Pa, the percentage of the non-condensable gases is 1.5×10^–5, the simulation is steady and no slip is considered on the walls.

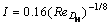                       (13)

where I is the turbulence intensity; Re is the Reynolds number; and D_H is the hydraulic diameter.

2.4 Characteristic coefficients

An important parameter in the analysis of cavitation in control valves is the cavitation number, which is used to predict the occurrence of cavitation, and is expressed as:

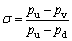                            (14)

where p_u is the upstream pressure; p_v is the saturation vapor pressure at the fluid’s working temperature and p_d is the downstream pressure.

Another important parameter in the design of control valves is the flow coefficient, which relates the pressure loss along the valve to the flow rate of the fluid. In the metric system, the flow coefficient is indicated by K_v, which is defined as follows:

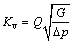                            (15)

where Q is the flow rate; G is the specific gravity of the fluid, which is equal to 1.0 at the temperature of 16 °C; △p is the pressure drop along the valve.

2.5 Initiation point of cavitation

In experimental works, the noise and vibration generated by the collapse of the cavitation bubbles can be used to determine the initiation point of cavitation. This method cannot be employed in numerical analysis to find the initiation point of cavitation, and for this purpose, a new quantitative parameter is needed.

By examining the changes of the maximum vapor volume fraction with the input flow rate at different valve stem travels, it was determined that the maximum volume fraction of vapor increases with the increase of the input flow rate, and that this increase is immense at the onset of cavitation (Figure 4). In this study, the maximum vapor volume fraction interval of 0.1–0.15 was considered as the initiation point of cavitation (outlined in the figure by two red dashed lines). The reason for selecting this interval as a criterion for the onset of cavitation is that at the maximum vapor volume fractions of less than 0.1, cavitation forms very sparsely and the convergence of the numerical solution is slow. And at the maximum vapor volume fractions of more than 0.15, we move away from the onset of cavitation, and this interval cannot be deemed suitable for the initiation point of cavitation.

Figure 4 Changes of maximum vapor volume fraction with inlet flow rate

3 Results

For convergence criterion, all scaled residuals were below 10^–5, and six sensors, which were placed in different points along the flow field, were used to monitor velocity, pressure and the vapor volume fraction. In all cases, iterations continued until the magnitude of the velocity, pressure and the vapor volume fraction measured by the sensors became constant.

Figures 5(a)–(c) illustrate the distribution of pressure in the symmetry plane for 75% of the full control valve stem travel in 4 different cases. The upstream pressure of the control valve is 6.0×10³ kPa and its downstream pressure is 2.0×10³ kPa. In the control valve without trim (Figure 5(a)), a considerable pressure drop occurs between the seat and plug, and the fluid’s local pressure becomes less than the vapor pressure of water, and cavitation ensues. The low-pressure region can be clearly observed between the seat and plug at the valve outlet section. By adding a trim (Figure 5(b)), the pressure drop occurs in two stages. The main pressure loss occurs at the trim, and the subsequent pressure drop occurs between the seat and plug. In this case, the low-pressure region around the seat in the outlet section shrinks considerably.

In the cases where two and three trims are used (Figures 5(c) and (d)), the pressure diminishes in three and four stages, respectively, and the low-pressure region between the seat and plug goes away completely, and cavitation does not form in this plane. Also, it is noted that there is not much difference between pressure distributions in the two and three trims.

Figure 6 shows the streamlines in the symmetry plane for 90% of the full control valve stem travel in 4 different cases. The downstream pressure is 2.0×10³ kPa and the mass flow rate is 35 kg/s. In the no-trim case (Figure 6(a)), a large vortex is observed under the seat. By adding the trims (Figures 6(b)–(d)), the vortices diminish in size and become less intense. Moreover, not much difference exists between the streamlines of the two and three trims’ cases.

In general, the cavitation formation zone is around the seat, near the trims and at the outlet section of the control valve. In this study, to carefully examine the regions where cavitation forms, the profiles of the vapor volume fraction isosurfaces have been used.

Figure 7 shows the isosurfaces at the vapor volume fraction of 0.12, 90% of the full control valve stem travel, downstream pressure of 2.0×10³ kPa (absolute) and mass flow rate of 35 kg/s. The cavitation formation regions which, in the no-trim case (Figure 7(a)) were around the seat and the lower section of valve, with the addition of a trim (Figure 7(b)), move to the vicinity of trim, and the intensity of cavitation around the seat drastically diminishes. In the cases in which two and three trims are used (Figures 7(c) and (d)), cavitation disappears around the trims and its intensity over the seat considerably diminishes. Obviously, there is not much difference between the two and three trims’ cases in terms of the formation region and the intensity of cavitation. In investigating valve openings at less than 75% of the full control valve stem travel, it was observed that cavitation only forms around the seat, and by adding the trims, its formation region does not change. Also, cavitation always exists at the valve outlet and its condition does not change with the addition of trims.

Figure 8 shows the diagram of the cavitation numbers at the initiation point of cavitation for different control valve stem travels. In this curve, the cases of no-trim, one trim, two trims and three trims have been compared with each other. The sections below and above each curve indicate the ‘cavitation zone’ and ‘safe zone’, respectively. So, one should try to select a control valve whose operating zone is above the noted curve. By adding the trims and increasing their quantity, the control valve operates in a more extended range without the occurrence of cavitation. The safe zone of cavitation broadens by 40%, 56% and 58% after adding one, two and three stage trims respectively for the 50% of valve opening. It is clear that the effect of these trims on the reduction of the cavitation zone diminishes with the increase in the number of trims.

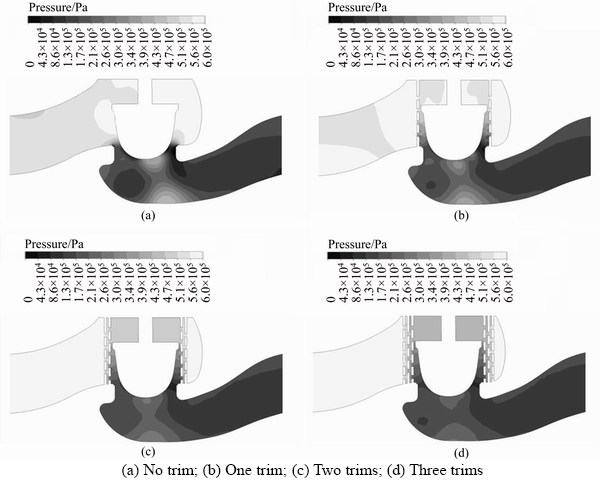
Figure 5 Distribution of pressure in symmetry plane for 75% of full control valve stem travel:

Figure 6 Streamlines in symmetry plane for 90% of full control valve stem travel:

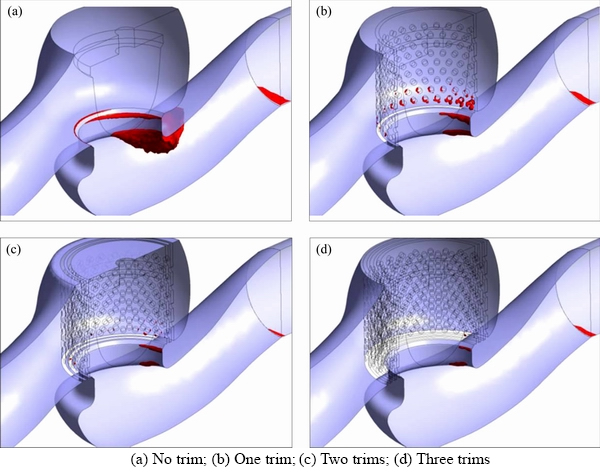
Figure 7 Isosurfaces at vapor volume fraction of 0.12 and 90% of full control valve stem travel:

Figure 9 illustrates the flow coefficients of the control valve at different control valve stem travels and different number of trims. Since the cavitation bubbles reduce the effective cross section of the passing fluid, the flow coefficient of the valve diminishes as a result of this phenomenon. Therefore, to eliminate the effect of the cavitation on the flow coefficient, all the data in this diagram have been obtained for a state of no-cavitation (at mass flow rates lower than those required for the start of cavitation). In all the cases, with the further opening of the control valve, the flow coefficient increases.

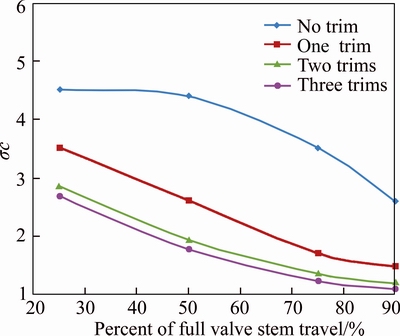
Figure 8 Cavitation numbers for different control valve stem travels at initiation point of cavitation

Figure 9 Flow coefficients at different control valve stem travels

By adding one trim, the flow coefficient decreases by 31 in full valve stem travel, while by adding the second trim, the reduction of the flow coefficient becomes almost half of the preceding case. The reduction in flow coefficient is negligible for low valve opening and as the stem travel increases, the decrease in flow coefficient becomes more considerable. So, in general, by increasing the number of trims, the flow coefficient diminishes, and this reduction is substantial at first, but becomes less so as the quantity of trims increases.

Due to the increase in the number of trims, at a constant pressure difference between inlet and outlet (constant cavitation number), the mass flow rate diminishes, and so does the velocity of the incoming fluid. In view of Bernoulli’s equation, with the reduction of velocity along the streamline, pressure increases, leading to the reduction of cavitation intensity. Therefore, the reduction of cavitation intensity at a constant pressure difference between inlet and outlet is somewhat due to the reduction of the incoming flow rate; while the goal of this study is to investigate the effect of the multi-stage pressure drop by the trims on cavitation. Therefore, the effects of the different numbers of trims cannot be easily compared at a constant pressure difference. So, for a more exact analysis of trims effect, the flow rate for the onset of cavitation was used.

Figure 10 shows the mass flow rates for the initiation of cavitation at different control valve stem travels and numbers of trims. The sections above and below the curve designate the ‘cavitation zone’ and ‘safe zone’, respectively. With the increase in the number of trims, cavitation occurs at a higher flow rate. As one may notice, for the half valve opening, the flow passes through the valve will increase by 82% after putting three stages trims relative to the no-trim case which is due to the less cavity occurrence in the flow pathways. At valve stem travels of more than 50%, the increase in flow rate is significant; whereas at valve stem travels of less than 50%, the increase in flow rate is slight, and even in the cases of two and three trims, the flow rates for cavitation onset do not differ. In general, due to the high cost of trims and also the significant reduction of the valve’s flow coefficient as a result of increase in the number of trims, it is recommended to use two trims; except in cases in which the valves are set to operate at large openings, where, at most, three trims can be utilized. It should be noted that, at flow rates greater than the cavitation onset flow rate (at least 1.5 times the cavitation onset flow rate), a three trims’ case shows its effectiveness, and in these circumstances, cavitation is less intense relative to when two trims are used.

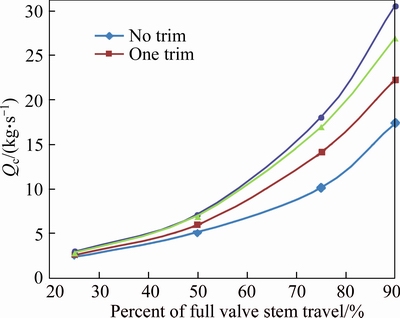
Figure 10 Mass flow rates for different control valve stem travels at initiation point of cavitation

Figure 11 shows the comparison of results obtained from numerical analysis with empirical data for a traditional valve without trim. At valve stem travels of less than 10%, differences exist between the empirical data and numerical analysis; however, at valve stem travels of more than 10%, a good agreement can be observed between the numerical analysis results and empirical data. The experimental uncertainty calculated, ranged from 2.89% to 9.56%.

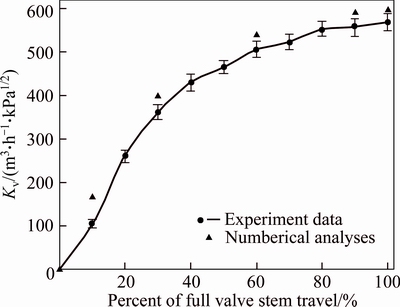
Figure 11 Flow coefficient for traditional valve (experiment uncertainty range is from 3.51% to 9.56%)

4 Conclusions

In this study, by means of numerical analysis, the globe control valve was investigated in four different cases (no-trim, one trim, two and three trims) and the effects of the number of trims on the initiation point, location and intensity of cavitation were studied. It was found that in the control valve without trim, a sudden pressure drop occurs between the seat and the plug; while, after adding the trims, a multi-stage pressure drop occurs around the trims and the fluid’s local pressure reaches the saturation vapor pressure in fewer regions. In all the cases, at valve stem travels of less than 75%, cavitation occurs over the seat at the outlet section of the valve. However, at valve stem travels of more than 75%, cavitation forms over the seat in the valve without trim; and by adding the trims, cavitation moves over the trims. Adding the trims also makes the control valve operate in a vaster operating range without cavitation; in other words, cavitation occurs at higher flow rates. Another effect of adding the trims is that the vortices created under the seat become less intense, which causes a decline in the vibration of the pipes. In addition to all the effects discussed above, by increasing the number of trims, the valve’s flow coefficient considerably decreases. In general, the addition of one and two stage trims significantly reduces the cavitation intensity relative to the valve without trim and delays the occurrence of cavitation. However, there is not much difference between the two and three trims’ cases in terms of the intensity and initiation point of cavitation. Therefore, due to the high cost of making the trims and the substantial reduction of flow coefficient, it is not recommended to increase the number of trims to more than three.

Nomenclature

f

Mass fraction

F

Body force

G

Specific gravity of the fluid

I

Turbulence intensity

k

Turbulent kinetic energy

K_v

Flow coefficient

p

Pressure

Q

Mass flow rate

R

Evaporation rate

u_m

Mass-averaged velocity

α_v

Volume fraction of vapor

γ

Effective exchange coefficient

ε

Dissipation rate

μ_m

Mixture viscosity

μ_t

Turbulent viscosity

ρ_m

Density of mixture

ρ_l

Density of liquid

ρ_v

Density of vapor

σ

Cavitation number

References

[1] SHEN W, ZHANG J, SUN Y, ZHANG D J, JIANG J H. Effect of cavitation bubble collapse on hydraulic oil temperature [J].Journal of Central South University,2016, 23(7): 1657–1668. DOI: 10.1007/s11771-016-3220-z.

[2] CASADA D. Throttled valve cavitation and erosion. ORNL/NRC/LTR-91/25 [R]. 1991.

[3] YUZAWA S, OKUTSU R, HASHIZUME T, OUTA E. Cavitation erosion features in industrial control valves at an inlet pressure of 20 MPa [J].JSME International Journal Series B Fluids and Thermal Engineering, 1998, 41(4): 1105–1113. DOI: 10.1299/jsmeb.41.1105.

[4] DAVIS J A, STEWART M. Predicting globe control valve performance—Part I: CFD modeling [J]. Journal of Fluids Engineering, 2002, 124(3): 772–777. DOI: 10.1115/ 1.1490108.

[5] CHERN M J, WANG C C. Control of volumetric flow-rate of ball valve using V-port [J]. Journal of Fluids Engineering, 2004, 126(3): 471–481. DOI: 10.1115/1.1760536.

[6] MAYNES D, HOLT G, BLOTTER J. Cavitation inception and head loss due to liquid flow through perforated plates of varying thickness [J]. Journal of Fluids Engineering, 2013, 135(3): 031302. DOI: 10.1115/1.4023407.

[7] AMIRANTE R, CATALANO L A, POLONI C, TAMBURRANO P. Fluid-dynamic design optimization of hydraulic proportional directional valves [J]. Engineering Optimization, 2014, 46(10): 1295–1314. DOI: 10.1080/ 0305215X.2013.836638.

[8] DINA M. Detection of cavitation phenomenon in a centrifugal pump using audible sound [J]. Mechanical Systems and Signal Processing, 2003, 17(6): 1335–1347. DOI: 10.1006/mssp.2002.1514.

[9] MARTIN C S, MEDLARZ H, WIGGERT D C, BRENNEN C. Cavitation inception in spool valves [J]. Journal of Fluids Engineering, 1981, 103: 564–575. DOI: 10.1115/1.3241768.

[10] GAO Hong, FU Xin, YANG Hua-yong, TSUKIJI T. Numerical investigation of cavitating flow behind the cone of a poppet valve in water hydraulic system [J]. Journal of Zhejiang University: Science B, 2002, 3(4): 395–400. DOI: 10.1007/BF02839479.

[11] AN Y J, KIM B J, SHIN B R. Numerical analysis of 3-D flow through LNG marine control valves for their advanced design [J]. Journal of Mechanical Science and Technology, 2008, 22(10): 1998–2005. DOI: 10.1007/s12206-008- 0745-6.

[12] RAMMOHAN S, SASEENDRAN S, KUMARASWAMY S. Effect of multi jets on cavitation performance of globe valves [J]. Journal of Fluid Science and Technology, 2009, 4: 128–137. DOI: 10.1299/jfst.4.128.

[13] MU D, LI C. A new mathematical model of twin flapper-nozzle servo valve based on input-output linearization approach [C]// Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC), 2011 2nd International Conference on. IEEE, 2011: 3662– 3666. DOI: 10.1109/AIMSEC.2011.6009893.

[14] CHERN M J, HSU P H, CHENG Y J, TSENG P H, HU C M. Numerical study on cavitation occurrence in globe valve [J]. Journal of Energy Engineering, 2012, 139(1): 25–34. DOI: 10.1061/ (ASCE)EY.1943-7897.0000084.

[15] JIN Z J, WEI L, CHEN L L, QIAN J Y, ZHANG M. Numerical simulation and structure improvement of double throttling in a high parameter pressure reducing valve [J]. Journal of Zhejiang University: Science A, 2013, 14(2): 137–146. DOI: 10.1631/jzus.A1200146.

[16] AMIRANTE R, DISTASO E, TAMBURRANO P. Experimental and numerical analysis of cavitation in hydraulic proportional directional valves [J]. Energy Conversion and Management, 2014, 87: 208–219. DOI: 10.1016/j.enconman.2014.07.031.

[17] AUNG N Z, LI S. A numerical study of cavitation phenomenon in a flapper-nozzle pilot stage of an electrohydraulic servo-valve with an innovative flapper shape [J]. Energy Conversion and Management, 2014, 77: 31–39. DOI: 10.1016/j.enconman.2013.09.009.

[18] WHITE F M. Fluid mechanics [M]. Boston: McGraw-Hill, 2003.

[19] INCORPORATION F, FLUENT User’s guide version 6.3 [M]. Lebanon, NH, USA: FLUENT Inc., 2005.

[20] VAGHEFI M, SAFARPOOR Y, AKBARI M. Numerical investigation of flow pattern and components of three-dimensional velocity around a submerged T-shaped spur dike in a 90° bend [J].Journal of Central South University, 2016,23(11): 2984–2998. DOI: 10.1007/s11771- 016-3362-z.

[21] MARGOT X, HOYAS S, GIL A, PATOUNA S. Numerical modelling of cavitation: Validation and parametric studies [J]. Engineering Applications of Computational Fluid Mechanics, 2012, 6(1): 15–24. DOI: 10.1080/19942060.2012.11015399.

[22] SINGHAL A K, ATHAVALE M M, LI H, JIANG Y. Mathematical basis and validation of the full cavitation model [J]. Journal of Fluids Engineering, 2002, 124(3): 617–624. DOI: 10.1115/1.1486223.

[23] LAUNDER B E, SPALDING D B. Lectures in mathematical models of turbulence [M]. New York: Academic Press, 1972.

[24] FRANC J P, MICHEL J M. Fundamentals of cavitation [M]. Springer Science & Business Media, 2006.

[25] ROUSE H. Cavitation and pressure distribution: Head forms at zero angle of yaw [M]. 1948.

(Edited by YANG Hua)

中文导读

不同气蚀次数球阀空化的数值研究

摘要：空化是控制阀中的一种破坏性现象。为了延缓空化，采用一种多孔圆柱板，称为trim。在此之前，我们曾研究过孔板直径和不同类型的trim的影响。本文采用4种不同工况(无trim，1，2和3 trims)对球阀进行数值分析，分析了trim的数量对气蚀强度、形成区域和空化起始点的影响。结果表明，与不加trim的阀门相比，增加一个或两个trim可以降低气蚀的强度，延缓空化的发生。然而，在使用两到三个trims的情况下，空化的强度和起始点没有明显的差异。由于trim生产成本高，流量系数严重下降，将trim数量增加到3个以上在经济和技术上都是不合理的。

关键词：数值分析；抗空化调整；球阀

Received date: 2017-06-25; Accepted date: 2018-03-21

Corresponding author: Mansour ALIZADEH, Assistant Professor; Tel: +98-21-77240540; E-mail: ma_alizadeh@iust.ac.ir; ORCID: 0000-0002-9631-0593