J. Cent. South Univ. (2020) 27: 76-87

DOI: https://doi.org/10.1007/s11771-020-4279-0

A new hybrid energy absorption mechanism subjected to axial loading

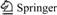
BAHMAN Paygozar¹, MOHAMMAD ALI Saeimi Sadigh²

1. Department of Mechanical Engineering, TED University, Ankara, Turkey;

2. Department of Mechanical Engineering, Azarbaijan Shahid Madani University, Tabriz, Iran

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: This study aims to introduce a novel hybrid design with a combination of two more common mechanisms for improving the capacity of systems in absorbing the kinetic energy of moving vehicles or devices. This new model consists of two individual mechanisms, i.e., expansion of a circular tube accompanied by crushing of an inner tube, which dissipate the energy through friction, plastic deformations and failures of inner tube. This study comprises 24 case studies surveyed under two different design controls, constant mass and constant volume, for comparing purposes. Finite element simulations are utilized so as to investigate models’ deformations and to extract some crashworthiness parameters in aid of representing the efficiency of the mechanism as well as conducting a parametric study between three different profiles of inner tube. This study shows that models with inner circular and hexagonal tube profile absorb higher amount of energy due to experiencing three different modes of energy dissipation systems, including folding, shear and ductile damages.

Key words: energy absorption; specific energy; hybrid mechanism; finite element

Cite this article as: BAHMAN Paygozar, MOHAMMAD ALI Saeimi Sadigh. A new hybrid energy absorption mechanism subjected to axial loading [J]. Journal of Central South University, 2020, 27(1): 76-87. DOI: https://doi.org/10.1007/s11771-020-4279-0.

1 Introduction

Absorbing the kinetic energy of vehicles is a significant goal owing to improving the safety of both passengers and vehicles, in case of both active and passive accidents. In this regard, different modes of energy absorber systems have been introduced and improved during recent years. One of the most useful methods for the purpose of absorbing the kinetic energy of moving devices is the use of two circular tubes (a deformable tube expanded by another deformable or rigid one). This common sort of energy absorber system is more practically investigated by many researchers [1-4]. In this method, the energy is dissipated through the friction and plastic deformations. Another usual mechanism for this purpose, works through crushing a tube, which could be in different shapes, by means of a rigid plate [5-10]. This mechanism dissipates the energy by plastic deformations and also complete failure of the deformable tube while crushing.

To improve the capacity of the energy absorption, some researches have recently been done, in which some methods have been introduced. For instance, XIE et al [11] investigated a system consisting of multi-cell, square, thin-walled tubes in order to improve the capability of the energy absorption mechanism. They found out that side-length of the exterior tube had a direct effect on the crushing force but little influence on the absorbed energy. In addition, both parameters were less sensitive to side-length of the interior tube. They also, investigated the effects of some dimensional parameters on the specific absorbed energy in addition to mean and peak crushing forces [12]. As a result, it was observed that the number of cells used in the structure and wall thickness of the construction had direct relationships with the aforementioned parameters; however, increasing the side-length affected the parameters slightly. Another kind of improvement was investigated by QIU et al [13], which surveyed the amount of absorbed energy while using multi-cell hexagonal columns. They mainly examined the best possible sectional configuration under multiple loading angles and found out that mid-edge connected hexagonal column was the best bi-tubular configuration, according to maximum carried load as well as the amount of absorbed energy, through employing complex proportional assessment method. In a similar way, SHARIFI et al [14] surveyed bi-tubular circular systems in order for the improvement of the system capacity. They investigated three different parameters, including tube thickness and diameter as well as the interaction between two tubes. They proposed two feasible solutions in aid of improving crashworthiness parameters, i.e., the use of two tubes in different length and cutting grooves at the end of either tube. Similarly, PAYGOZAR and SAEIMI SADIGH [15] improved the capacity of the circular tubes by welding lateral annular and vertical parts. They investigated the efficiency of the systems and found out that the improved models dissipated more energy than a simple circular tubes system in the same weight. Another related study was done by LI et al [16], which combined two different energy absorption mechanisms. They studied a model consisting of a mandrel expanding the tube in addition to a blade for cutting purposes. This absorbed the energy through the plastic expansions and the tube splitting. As a result, they drawn that the expansion mechanism absorbed more energy than splitting system.

On the other hand, in the case of improving the second aforementioned mechanism, AZARAKHSH et al [17] surveyed a foam-filled bi-tubular model crushed by a rigid plate. They used two coaxial brass-made tubes and foam in between. It was found that system capacity was improved measurably, although the construction lost its weight efficiency. Similarly, LIU et al [18] studied crashworthiness of the cylindrical tubes filled with conventional and negative Poisson ratio foams and found that systems with sandwich double tubes filled with mixed Poisson ratio foam have better absorption capacity in comparison with those filled with either positive or negative Poisson ratio foam. WANG et al [19] investigated the absorption capability of connectors filled by aluminum foam under the impact loading. They utilized aluminum foam as filler to improve the pleated plates outside and consequently found progress in the energy absorption capacity.

The present study is a novel design of energy absorber system which enjoys a new mechanism consisting of two individual practical mechanisms. This study aims to introduce a novel hybrid mechanism that enhances the amount of absorbed energy in favor of optimizing of the system’s occupied space. This model includes an aluminum tube in the center of structure surrounded by a steel tube in addition to a rigid conical mandrel which is responsible for the expansion of the steel circular tube as well as crushing the aluminum tube. Moreover, this study investigates three different profiles of the aluminum tube in order to signify the most efficient configuration of the model. For this purpose, two main crashworthiness parameters were drawn and compared. The most possible usage of the proposed model can be in the body of roadside utilities like lamp-posts or even in front of the gas stations or special places, by which as much vehicles kinetic energy as possible can be absorbed in case of crash, while occupying a little space with the aid of placement of one mechanism inside another. This kind of utility can be located inside a suitable frame able to be mounted in roadside devices or to be put individually in the likely places for accident.

2 Model definition

Hybrid mechanism of this study dissipates the energy using two individual methods: expansion of circular tubes (ECT) and axial crushing tubes (ACT). Figure 1 shows the configurations of these models [20, 21]. In ECT model (Figure 1(a)), a rigid conical mandrel expands the deformable tube circumferentially and dissipates the energy through plastic deformations and friction. Figure 1(b) shows ACT model, in which a rigid moving plate impacts the deformable tube and causes the tube to be crushed. The plate with an initial velocity crushes the tube into the rigid base and dissipates the kinetic energy through the tube plastic deformations and tube failures.

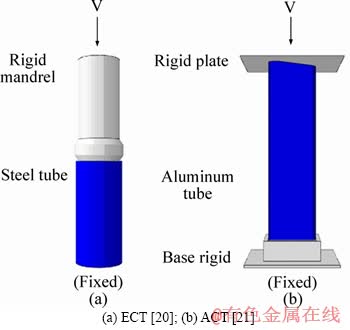
Figure 1 General configurations of two ordinary mechanisms:

As discussed previously, hybrid mechanism is a combination of two individual viable methods of energy absorption, which dissipates the kinetic energy through friction, plastic deformations, and complete failure of the deformable tube. In general, the model consists of two deformable tubes described before as well as two rigid parts, a conical mandrel in the top of the system and another in the bottom for the purpose of supporting the system, in other words, a rigid plate holding the other parts in position. In case of a crash, the mandrel is press-fitted into the deformable steel tube, and consequently it expands the deformable tube circumferentially and simultaneously it impacts the aluminum tube. Figure 2 shows a general layout of a hybrid model in addition to some relevant constant dimensions. It is worth mentioning that considering the placement of an ACT model into an ECT model, the volume of the system with and without the central part is the same. It was assumed that the outer tube was welded to the rigid plate, while the inner tube was press-fitted into the raised hollow section of the rigid plate. Concerning accurate, correct assembly of the system, it should be mentioned that the mandrel and both tubes are considered coaxial.

This study investigates twenty four case studies under two different designs: constant mass (CM) and constant volume (CV). In other words, first design relates to models with a constant mass of inner tube, while the second one refers to models with a constant inside volume of inner tube. It is worth noting that the dimensions of both mandrel and steel circular tube are the same in all models. However, the geometry of the inner tube is changed from one model to another. This part of case studies are generally in three different shapes: rectangular, circular and hexagonal. A parametric illustration of the aluminum tube in three different profiles shown in Figure 3.

3 Theory and material characterization

3.1 Material definition

The hybrid energy absorber system contains an inner tube which is made of aluminum alloy EN AW-710 T6, with high energy absorbing capacity. In this regard, an exact definition of its mechanical characteristics was vital for the sake of the accurate numerical simulation of plastic deformations and material failure. To simulate large deformations and the failure, rate-dependent plasticity behavior of aluminum in addition to two main failure models (ductile and shear failure) were defined.

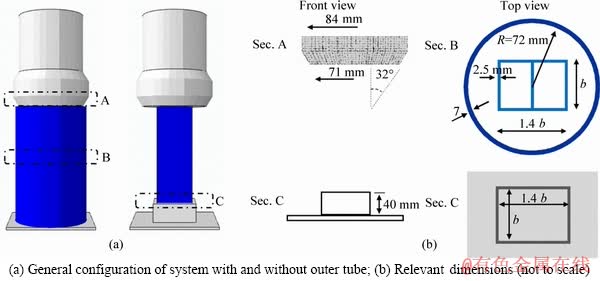
Figure 2 Geometry of hybrid mechanism:

Figure 3 Configuration of three types of aluminum tubes:

In all analyses, plastic anisotropy and strain hardening were considered. Equation (1) was utilized to define material plasticity. In this equation, a and n are material constants, ε₀ is analytical approximation constant and ε_eq is the equivalent strain.

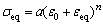                          (1)

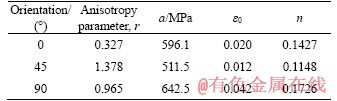
Material parameters used in this equation were calculated at 0°, 45° and 90° with respect to the extrusion direction and are collected in Table 1. According to the table and the values of the plastic anisotropy (r), it is clear that this parameter cannot be neglected.

Table 1 Material parameters of EN AW-7108 T6 [21]

Strain sensitivity of the material was defined by the use of the adiabatic flow stress curves (see Figure 4). In order for the simulations of rate-dependent plasticity and explicit dynamic time integration scheme, the incorporation of the strain rate features of the material was precondition. Damage initiation and propagation of the crushing tube were modeled with the aid of ductile and shear fracture criteria.

KOLMOGOROV [22] introduced a criterion which can be used to denote fractures.

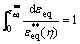                              (2)

In ductile material, is assumed as a function of stress triaxiality (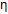), defined as follows:

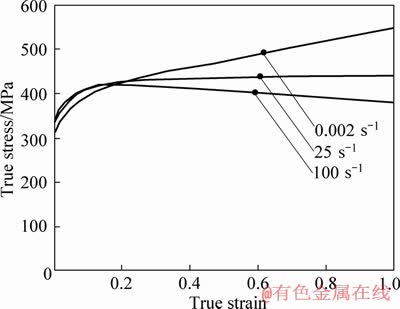
Figure 4 Adiabatic flow stress versus strain [21]

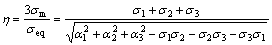  (3)

The relationship between equivalent fracture strain and stress triaxiality is shown below:

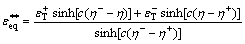      (4)

where c is an orientation-dependent parameter;

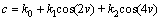                  (5)

Moreover, in order to simulate shear fracture, 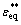 is defined as a function of variable θ, as follows:

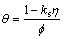                                (6)

where k_s is a material parameter and Ф is the ratio of maximum shear stress and equivalent stress.

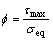                                 (7)

Equation (8) demonstrates the equivalent plastic strain for shear fracture, as follows:

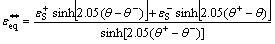  (8)

Table 2 has material parameters of Eqs. (4) and (8).

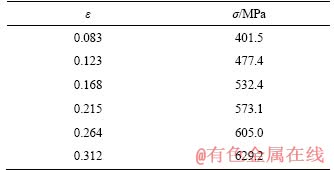
On the other hand, the hybrid energy absorber system contains an outer steel tube which absorbs the energy through circumferentially plastic deformations. Taking large deformations of the steel tube into account, material behavior of the tube was considered elastic-plastic when the conical mandrel was rigid. The true stress-strain data for steel tube, adopted from Ref. [20], are summarized in Table 3.

Table 2 Ductile and shear fracture material parameters of EN AW-7108 T6 [1]

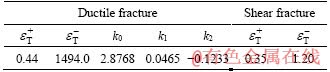
Table 3 Stress-strain relationship of deformable steel tube material [2]

3.2 Crashworthiness parameters

In respect of comparing investigated models and predicting the most preferable model, definitions of some parameters are crucial. In this regard, both plastic and frictional dissipation energy are extracted from finite element package. These values are required to compute total amount of absorbed energy (E_tot), described as a summation of plastic and frictional dissipation energy. On the other hand, this parameter is related to the total integral of the load-displacement curve with respect to displacement [23, 24], as follows:

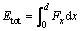                              (9)

where F_x and d are equivalent to the instantaneous axial load during crushing and total displacement, respectively.

In addition to two above-mentioned criteria, two other suitable parameters for investigations are specific absorbed energy when the mass and volume of the inner tube are constant, SAEM and SAEV, respectively. Equations (10) and (11) define two aforementioned parameters, as follows:

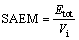                             (10)

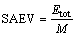                             (11)

where E_tot, V_i and M represent the total absorbed energy, the internal volume of aluminum tubes and the weight of aluminum tubes, respectively.

4 Numerical investigation

This part deals with finite element simulation techniques. In general, twenty-four case studies were numerically investigated in two different designs, constant mass and constant volume. The introduced hybrid model contains two different mechanisms, described previously. In order to validate the simulation of hybrid mechanism, initially, both inner and outer tubes were individually analyzed. Then, some hybrid case studies were analyzed to determine their efficiencies and preferences.

4.1 Validation process

To validate the simulation procedure, inner tube with ACT mechanism and outer tube with ECT mechanism were analyzed individually. This is because each mechanism of the hybrid system has no effect or interference on the other one.The validation for the outer part of the hybrid mechanism was previously done in a similar work [15]. To check the validity of the numerical part, the ECT mechanism was simulated according to an experimental work [20] with identical conditions and dimensions as introduced in the research. Figure 1(a) shows the general configuration of the sample. Given the sample in experiments [20], a mandrel with dimensions identical to that shown in Figure 2(b) (Sec. A), as well as a steel tube with a length and thickness of 200 mm and 4 mm, respectively, was modeled in the ABAQUS with an initial mandrel velocity of 6.39 m/s. The comparison between experimental and numerical results was shown in Figure 5(a). In addition, a similar experiment was designed in this study to validate the numerical simulations in the other way. In this experiment, two identical tubes with the lengths and diameter of 50 and 40 mm, respectively, and with the thickness of 2 mm, were utilized so as to survey the precision of the numerical investigations. The length of the tubes was considered small due to stabilization of the load- displacement curve after a little displacement of the moving tube and to limitation of the testing machine. To do experiment, a drop-hammer was employed in order to simulate the crash with a rigid plate hitting the system with an initial velocity, including specific kinetic energy.

Figure 6 indicates the apparatus in addition to a sample while and after deformation. Figure 7 shows the stabilization of the load-displacement curve after a movement of 15 mm, and a good agreement between the numerical and experimental results.

Figure 5 Comparison between load-displacement diagrams of numerical models and corresponding experiments:

Figure 6 Experiment used to validate ECT mechanism of hybrid mechanism:

For the inner mechanism,the ACT model with aluminum rectangular tube, was analyzed numerically and the results are plotted against those from experiments carried out by HOOPUTRA et al [21], which was also presented in the ABAQUS documentation as an example [25]. The general configuration of the experimental model used to validate the ACT mechanism was plotted in Figure 1(b). The variable dimension of ACT, b, as illustrated in Figure 2(b), was considered equal to 71 mm. The length of the tube was taken 400 mm as well. An initial velocity of 10 m/s, was imposed on the impactor rigid plate. Figure 5(b) shows a very good agreement between load-displacement responses of the validated model and the experimental data [21].

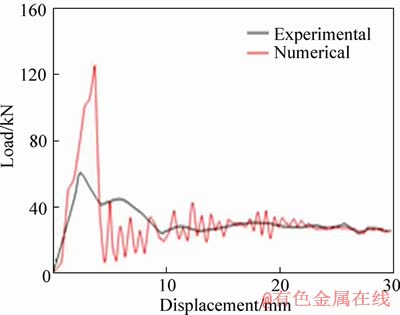
Figure 7 Comparison between load-displacement diagrams of designed experiment and corresponding numerical models (Validation of the test carried out via apparatus in Figure 6)

4.2 Finite element analyses

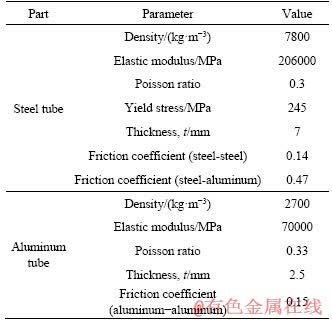
A finite element package, ABAQUS/Explicit, was used for the simulations of this study. In all models, two rigid parts as well as two tubes are meshed by 4-node quadrilateral surface element and 8-node linear brick which denoted by SFM3D4R and C3D8R, respectively. Mesh sensitivity study was conducted, and subsequently a mesh size of 2.5 and 5 mm was chosen for inner and outer tube, respectively. Moreover, four and two layers of elements were used in the thickness of steel and aluminum tubes, respectively. In addition, the Coulomb friction along with an explicit surface- to-surface contact interaction was employed between all surfaces in contact. Concerning boundary condition, a clamped constraint was applied to the base plate in order to fix the model and also the bottom of the steel tube was fixed in two transverse directions. In all case studies, the velocity of the conical mandrel was considered equal to 10 m/s, for comparing purposes. Table 4 shows all relevant material properties which are constant in all simulations as well as the friction coefficients between two surfaces of different materials. It is worth mentioning that the length of tubes are variable according to each case study. In this regard, the corresponding tube length of each sample is gathered in the last two tables of this study.

Table 4 Finite element parameters of both steel and aluminum tubes [1, 2]

5 Results and discussion

In this study, a hybrid model was introduced, and subsequently some case studies of this model were analyzed numerically. In the first part of study, the efficiency of the hybrid model was compared to the efficiency of CTE and ACT models. Then, twenty-four case studies of three different profiles under two different designs, constant mass and constant volume, were compared together according to four crashworthiness parameters.

5.1 Model efficiency

The system capacity for absorbing the kinetic energy is a valuable criterion for specifying the efficiency of the hybrid model. In this regard, the load-displacement diagram of the hybrid model was compared with that of each single mechanism, independently (see Figure 8). According to the figure, the curve relating to hybrid mechanism is the sum of two simple mechanisms utilized in it. As can be observed in this figure, applying hybrid mechanism of absorbing energy enhance the capability of the system which absorb higher amount of energy, by superposing the amounts of absorbed energy by each individual mechanism.

Overall, regarding the efficiency of hybrid mechanism, it should be pointed out that this mechanism improves an ECT model more significantly and controllably, or, more precisely, by mounting aluminum tubes in different shapes and thicknesses into an ECT, the energy absorption capacity of the mechanism can be managed accurately in aid of designing a favorite system with a limited and specific volume. This efficiency of hybrid mechanism can be intensified considering the volume of hybrid mechanism, especially while using that in a small limited volume into special devices, such as in small vehicles for the purpose of absorbing the kinetic energy during an active crash. This is because the secondary mechanism (ACT) is placed inside the internal space of a primary one (ECT), in other words, the general occupied volume of a hybrid mechanism is equal in size to that of an individual ECT mechanism. In brief, in the new model, the useless internal space of an ECT model could efficiently be utilized with the aid of placing an ACT mechanism for improving system capacity.

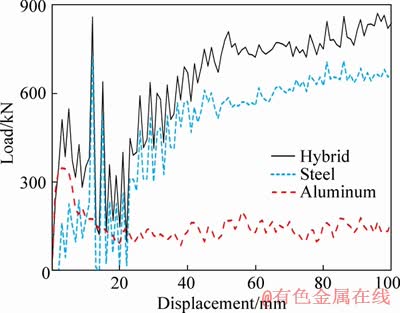
Figure 8 Comparison between load-displacement curves of hybrid mechanism and two individual models (case study RM2)

As another survey in proving the efficiency of the new mechanism, another hybrid model (RMS2-1) with a thicker inner tube was studied (see Figure 9). According to the figure, it is obvious that with an increase in the thickness of inner tube, from 2.5 to 4 mm, the load-displacement curve shifted upwards meaningfully, and consequently the total amount of absorbed energy surges from 60.4 to 71 kJ. This fact shows that in special use of energy absorber systems, especially while using it in a limited available space, a hybrid mechanism can be utilized including an ECT model as a main system improved by an ACT model, which is capable of undertaking different designs by changing the tube thickness in aid of enhancing the total amount of absorbed energy.

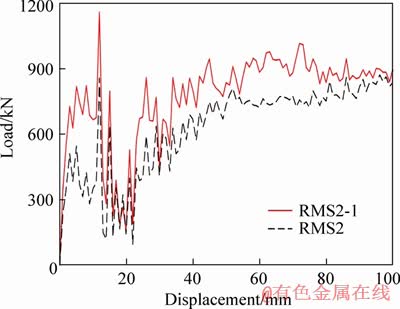
Figure 9 Comparison between load-displacement curves of hybrid mechanism (case study RMS2 with a thickness of 2.5 mm (RNS2) and 4 mm (RMS2-1)

5.2 Effect of tube geometry

In order to geometrically investigate the introduced model, the inner tube was analyzed in three common profiles (rectangular, circular and hexagonal) into two sets: constant mass and constant volume. For comparison purposes, two before-mentioned criteria, SAEM and SAEV, of all models were compared with each other. Tables 5 and 6 represent the results of this investigation in addition to some relevant variable parameters. These two tables classified all twenty four case studies into two main group according to their designs, constant mass (CM) and constant volume (CV). Each group of samples was categorized with respect to inner tube profile into three batches, each of which contains four specimens arranged in order of tube length from 175 mm to 250 mm.

According to Table 5, which represents the results of constant mass (CM) models, in the RMS models, the increase of length results in the decrease of energy absorption in the outer tube but the increase of energy in the inner tube. This causes in the hybrid system, a minimum value of SAEM value was experienced in all batches. This trend was followed by other two batches (CMS, HMS).Additionally, the effects of geometry can be investigated by comparing the SAEM values between three batches. Comparing the SAEM values for the hybrid models reveals that HMS models absorbs higher energy in comparison to the RMS and CMS models.

On the other hand in accordance with the models of constant volume (Table 6), with the increase of tube length the values of SAEV for both inner and outer tube has upward trend and consequently this amount of hybrid system raises noticeably. Considering the influence of geometry, it is evident that rectangular profile absorbs the lowest SAEV among three profiles. This amount is the highest for models of CVS in the cases with l=175 and 200 mm; however, in the cases with l=225 and 250 mm, SAEV value in HVS is the highest.

Table 5 Amount of absorbed energy in the case studies of CM design

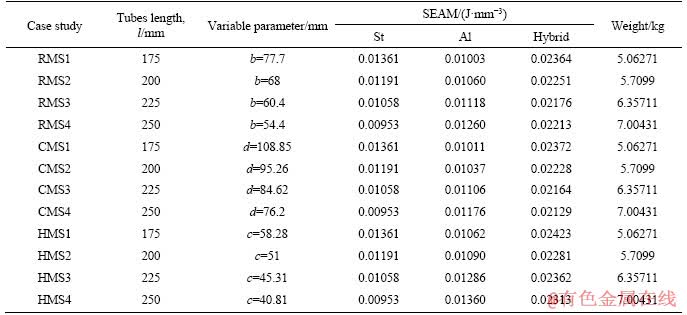
Table 6 Amount of absorbed energy in studies of CV design

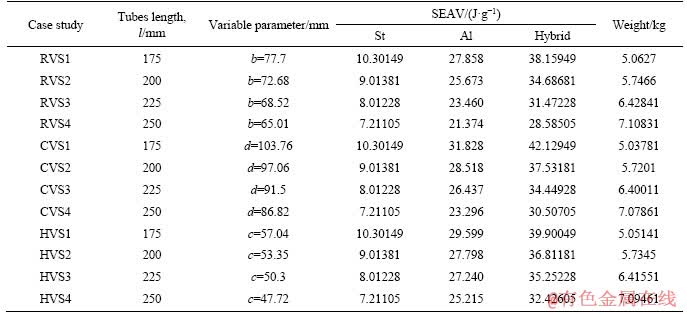
Table 5 shows that in the models of constant mass, the hybrid model with inner hexagonal tube of 250 mm in length (HMS4) dissipates the highest energy. Moreover, Table 6 depicts that in the models of constant volume, the hybrid model with inner circular tube in the length of 175 mm (CVS1) absorbs the highest energy. As a comparison between results of above tables, energy- displacement diagram of the HMS4 and CVS1 are presented in Figure 10. This figure shows that CVS1 with 5 kg weight absorbs slightly more energy than the HMS4 model with 7 kg weight.

In order to represent the deformation and failure trend of both inner and outer tubes of hybrid system while crushing, deformation counters of the models with different profiles are illustrated in Figure 11. In hybrid mechanism, plastic deformations including folding along with the ductile and shear modes of inner tube failure are mainly responsible for absorbing the energy in all case studies of current study. According to the figure, it is evident that folding occurred in all models. Figure 11(a) shows that folding and a slight shear damage at the corners of inner tube and dissipate the energy in rectangular tube. For the system with circular inner tube, the ductile damage in addition to two previously mentioned modes of energy dissipation systems occurs more severely,which may be the reason for its better function in absorbing energy (Figure 11(b)) in comparison to rectangular profile.

Figure 10 Comparison between amounts of absorbed energy (CVS1 versus HMS4)

According to Figure 11(c), three modes of folding, shear damage and ductile damage are responsible for energy absorbing during crush. In the similar fashion, this phenomenon results in better performance of hexagonal profile comparing to the rectangular profile. Moreover, deformations of the outer tubes are illustrated in Figure 11(d). This figure indicates that the outer tube undertakes just circumferentially expansion without any crushing or failures, during a crash.

6 Conclusions

In current research, a new hybrid mechanism was introduced in order to improve the system capacity in absorbing the kinetic energy of an impactor. This new model consists of two individual mechanism, expansion of a circular tube accompanied by crushing of an inner tube, which dissipates the energy through friction, plastic deformations and failure of inner tube. Overall, twenty four specimens in three different profiles of the inner tube and under two different model designs were numerically surveyed and subsequently the results were used for comparing purposes, according to four crashworthiness parameters. According to the observations, the following conclusions can be drawn:

1) This mechanism is effective and controllable owing to two reasons: the total absorbed energy is equal to that of each individual mechanism and this amount can also be controlled by changing the thickness of inner tube when the volume of whole system is considered a specific value. This fact makes the mechanism more feasible while using in special devices with limited space for placing the system.

2) In the models of constant mass, the hybrid model with the longest inner hexagonal tube profile dissipates the highest energy.

3) In the models of constant volume, the hybrid model with the shortest inner circular tube profile dissipates the highest energy.

4) As a comparison between models of constant mass and volume, the model including inner circular tube, with lower weight, dissipates slightly more energy than the model with inner hexagonal tube.

5) In the models with inner circular and hexagonal tubes, folding and damage energy absorption mechanisms are responsible for dissipating the kinematic energy, whereas in models of inner rectangular tubes, damage energy absorption mechanism is somewhat negligible.

Figure 11 Contour of deformable parts of hybrid models:

Nomenclature

F_x

Axial crushing load

F_tot

Total absorbed energy

b

Width of aluminum rectangular tube

d

Diameter of aluminum circular tube

M

Mass of the tubes

V_i

Internal volume of tubes

c

Side of aluminum hexagonal tube

l

Length of tubes

CM

Constant mass design

CV

Constant volume design

ECT

Expansion of circular tubes

ACT

Axial crushing tubes

CMS

Sample with circular inner tube and constant mass design

HMS

Sample with hexagonal inner tube and constant mass design

RVS

Sample with rectangular inner tube and constant volume design

CVS

Sample with circular inner tube and constant volume design

HVS

Sample with hexagonal inner tube and constant volume design

RMS

Sample with rectangular inner tube and constant mass design

SAEM

Specific absorbed energy under constant mass

SAEV

Specific absorbed energy under constant volume

References

[1] ALMEIDA B P P, ALVES M L, ROSA P A R, BRITO A G, MARTINS P A F. Expansion and reduction of thin-walled tubes using a die: Experimental and theoretical investigation [J]. International Journal of Machine Tools and Manufacture, 2006, 46(12): 1643-1652.

[2] SEIBI A C, BARSOUM I, MOLKI A. Experimental and numerical study of expanded aluminum and steel tubes [J]. Procedia Engineering, 2011, 10: 3049 -3055.

[3] SHAKERI M, SALEHGHAFFARI S, MIRZAEIFAR R. Expansion of circular tubes by rigid tubes as impact energy absorbers: Experimental and theoretical investigation [J]. International Journal of Crashworthiness, 2007, 12(5): 493-501.

[4] JAKIRAHEMED M D, DAVIDSON M J, VENKATESWARLU G, VENUGOPAL L. A study on effect of process parameters on the expansion of thin walled aluminium 7075 tubes [J]. International Journal of Advanced Science and Technology, 2011, 36(11): 83-93.

[5] KOHAR C P, MOHAMMADI M, MISHRA R K. INAL K. Effects of elastic-plastic behaviour on the axial crush response of square tubes [J]. Thin-Walled Structures, 2015, 93: 64-87.

[6] SALEHGHAFFARI S, TAJDARI M, PANAHI M, MOKHTARNEZHAD F. Attempts to improve energy absorption characteristics of circular metal tubes subjected to axial loading [J]. Thin-Walled Structures, 2010, 48(6): 379-390.

[7] SINGH A, PANDA S K. Parametric study on quasi-static crushing behaviour of flanged tubes under axial loading [J]. Materials Today: Proceedings, 2017, 4(2, Part A): 863-871.

[8] YANG Z, YAN H, HUANG C, DIAO X, WU X, WANG S, LU L, LIAO L, WEI Y. Experimental and numerical study of circular, stainless thin tube energy absorber under axial impact by a control rod [J]. Thin-Walled Structures, 2014, 82: 24-32.

[9] ZHANG X, LENG K, ZHANG H. Axial crushing of embedded multi-cell tubes [J]. International Journal of Mechanical Sciences, 2017, 131-132: 459-470.

[10] ZHANG X, ZHANG H, REN W. Axial crushing of tubes fabricated by metal sheet bending [J]. Thin-Walled Structures, 2018, 122: 252-263.

[11] XIE S, YANG W, WANG N, LI H. Crashworthiness analysis of multi-cell square tubes under axial loads [J]. International Journal of Mechanical Sciences, 2017, 121: 106-118.

[12] XIE S, YANG W, LI H, WANG N. Impact characteristics and crashworthiness of multi-cell, square, thin-walled, structures under axial loads [J]. International Journal of Crashworthiness, 2017, 22(5): 503-517.

[13] QIU N, GAO Y, FANG J, FENG Z, SUN G, LI Q. Crashworthiness analysis and design of multi-cell hexagonal columns under multiple loading cases [J]. Finite Elements in Analysis and Design, 2015, 104: 89-101.

[14] SHARIFI S, SHAKERI M, FAKHARI H E, BODAGHI M. Experimental investigation of bitubal circular energy absorbers under quasi-static axial load [J]. Thin-Walled Structures, 2015, 89: 42-53.

[15] PAYGOZAR B, SAEIMI SADIGH M A. Improved energy absorption mechanism: Expansion of circular tubes by rigid tubes during the axial crushing [J]. Journal of Failure Analysis and Prevention, 2018, 18(1): 174-182.

[16] LI J, GAO G, DONG H, XIE S, GUAN W. Study on the energy absorption of the expanding–splitting circular tube by experimental investigations and numerical simulations [J]. Thin-Walled Structures, 2016, 103: 105-114.

[17] AZARAKHSH S, RAHI A, GHAMARIAN A, MOTAMEDI H. Axial crushing analysis of empty and foam-filled brass bitubular cylinder tubes [J]. Thin-Walled Structures, 2015, 95: 60-72.

[18] LIU W, HUANG J, DENG X, LIN Z, ZHANG L. Crashworthiness analysis of cylindrical tubes filled with conventional and negative Poisson’s ratio foams [J]. Thin-Walled Structures, 2018, 131: 297-308.

[19] WANG Y, ZHAI X, YAN J, YING W, WANG W. Experimental, numerical and analytical studies on the aluminum foam filled energy absorption connectors under impact loading [J]. Thin-Walled Structures, 2018, 131: 566-576.

[20] YAN J, YAO S, XU P, PENG Y, SHAO H, ZHAO S. Theoretical prediction and numerical studies of expanding circular tubes as energy absorbers [J]. International Journal of Mechanical Sciences, 2016, 105: 206-214.

[21] HOOPUTRA H, GESE H, DELL H, WERNER H. A comprehensive failure model for crashworthiness simulation of aluminium extrusions [J]. International Journal of Crashworthiness, 2004, 9(5): 449-463.

[22] KOLMOGOROV W L. Spannungen deformationen bruch [M]. Metallurgija, 1970: 230-235.

[23] HANSSEN A G, LANGSETH M, HOPPERSTAD O . Static and dynamic crushing of square aluminium extrusions with aluminium foam filler [J]. International Journal of Impact Engineering, 2000, 24(4): 347-383.

[24] HANSSEN A G, LANGSETH M, HOPPERSTAD O S. Static and dynamic crushing of circular aluminium extrusions with aluminium foam filler [J]. International Journal of Impact Engineering, 2000, 24(5): 475-507.

[25] ZAHRAN M S, XUE P, ESA M S, ABDELWAHAB M M. A novel tailor-made technique for enhancing the crashworthiness by multi-stage tubular square tubes [J]. Thin-Walled Structures, 2018, 122: 64-82.

(Edited by HE Yun-bin)

中文导读

一种新型的轴向载荷作用下的混合吸能机制

摘要：本研究结合两种常见的机制以提高系统吸收移动车辆或设备动能的能力。该模型由两个独立的机制组成，即圆管的膨胀和内胎的破碎，通过内胎的摩擦、塑性变形和失效来耗散能量。本研究调查24个在恒质量和恒体积两种不同设计控制下的案例以进行比较。利用有限元模拟方法研究了模型的变形，提取了耐撞性参数，以反映机制的效率，并对三种不同的内胎外形进行了参数化研究。研究表明，内环型和六角形管型模型由于经历了折叠、剪切和延性损伤三种不同的能量耗散系统，吸收了更多的能量。

关键词：能量吸收；比能；混合动力机制；有限元

Received date: 2018-02-13; Accepted date: 2019-09-08

Corresponding author: BAHMAN Paygozar; Tel: +90-312-5850192; E-mail: bahman.paygozar@tedu.edu.tr; ORCID: 0000-0001-8492- 5497