基于组合广义形态滤波的大地电磁资料处理

李晋^{1, 2}，汤井田²，肖晓²，张林成²，张弛²

(1. 湖南师范大学 物理与信息科学学院，湖南 长沙 410081；

2. 中南大学 地球科学与信息物理学院，有色金属成矿预测教育部重点实验室，湖南 长沙，410083)

摘要：针对矿集区大地电磁强干扰的特征，构建组合广义形态滤波器，从时间域波形上探讨组合广义形态滤波对实测大地电磁强干扰的噪声压制效果。给出基于组合广义形态滤波的大地电磁资料处理流程，在人烟稀少、基本无电磁干扰的青海柴达木盆地进行试验研究，对包含比较单一的人工广域电磁干扰源的试验点进行组合广义形态滤波处理，横向对比时间域波形和视电阻率-相位曲线的改善情况。研究结果表明：该方法可以更加精确地勾勒出大尺度强干扰的轮廓特征，视电阻率-相位曲线的整体形态更加光滑、平稳，数据质量得到明显改善；由于该算法能有效提取暂态信号中的奇异信号，且只需进行加、减和比较运算，计算速度快，这对于在矿集区开展大地电磁强干扰的压制及资料处理具有一定应用价值。

关键词：组合广义形态滤波；大地电磁资料处理；矿集区；视电阻率-相位；强干扰压制

中图分类号：P631            文献标志码：A         文章编号：1672-7207(2014)01-0173-13

Magnetotelluric data processing based on combined generalized morphological filter

LI Jin^{1, 2}, TANG Jingtian², XIAO Xiao², ZHANG Lincheng², ZHANG Chi²

(1. Institute of Physics and Information Science, Hunan Normal University, Changsha 410081, China;

2 .Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education,

School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)

Abstract: Considering the characteristics of magnetotelluric strong interference in ore concentration area, the combined generalized morphological filter was conducted, and the noise suppression effect of measured magnetotelluric strong interference was discussed by combined generalized morphological filter from time domain waveform. The magnetotelluric data processing procedure was presented based on the combined generalized morphological filter, and the relevant experimental research was carried out in sparsely populated, Qaidam Basin in Qinghai Province, where there is almost no electromagnetic interference. Using the combined generalized morphological filter for processing relatively simple artificial sources of wide field electromagnetic interference test points, the improvement situations of both time domain waveform and apparent resistivity-phase curve were compared. The results show that the proposed method can more accurately present the outline characteristics of the large-scale strong interference, and apparent resistivity-phase curve of the overall morphology is more smooth and stable. Moreover, magnetotelluric data quality is significantly improved. Since the algorithm can effectively extract singular signal in the transient signal, and only needs operations of addition, subtraction and comparison, the calculation speed increases. These potential advantages for the ore concentration area to carry out magnetotelluric strong interference suppression and data processing have application value.

Key words: combined generalized morphological filter; magnetotelluric data processing; ore concentration area; apparent resistivity-phase; strong interference suppression

随着我国经济高速发展，资源储备急剧下降，现有能源和重要矿产资源对社会经济可持续发展的保证程度日渐减弱，导致资源的供需矛盾日益突出。为了满足我国经济的高速发展对各种资源的需求，必须提高资源勘查水平、增大勘探深度，不断向地球深部索取资源。2008年，“深部探测技术与实验研究”专项(SinoProbe)启动，标志着我国地球科学在深部探测领域拉开序幕^[1-3]。大地电磁测深法(magnetotelluric，MT)自20世纪50年代初由Tikhonov和Cagniard提出至今，以野外施工简便、成本低廉、探测深度大、垂向分辨能力和水平分辨能力高等优点，在探测地壳深部结构方面得到广泛应用^[4-5]。近年来，其应用范围得到了飞速拓展，已逐渐成为矿产资源勘查、地下水、地热资源勘探、油气普查、地震预报、岩石圈深部结构探测、固体矿产深部找矿、水文、海洋地质及环境地质调查等诸多领域中的一种重要手段，并取得了丰硕成果^[6-7]。目前，由于专项三(SinoProbe-03)需要在长江中下游的矿集区及经济发达区进行大地电磁探测工 作^[8-9]，但鉴于天然大地电磁场频带范围宽且本身信号微弱，实际观测到的大地电磁信号是典型的非线性、非平稳信号；同时，随着人类文明的不断发展，重工业密集等因素造成的环境噪声以及人类活动等因素造成的人文电磁噪声日益严重，导致大地电磁测深数据受到严重污染，大地电磁探测的抗干扰能力明显减弱。现有的大地电磁强干扰分离方法在矿集区实际应用和测试中表现出诸多不足，这一领域面临的困难和挑战也日益加剧^[10-14]。为了提高矿集区大地电磁测深数据质量，抑制噪声干扰已成为当务之急。研究大地电磁强干扰的特征，提出有针对性的大地电磁强干扰分离方法，对改善大地电磁测深数据质量以及对大地电磁法探测结果的处理和解释具有重要意义^[15-16]。数学形态学(mathematical morphology, MM)是一门建立在严谨数学推理基础上的科学，其基本思想是利用集合描述目标信号，集合各部分之间的联系用来说明目标信号的结构特征，即通过设计1个“探针”即结构元素，其类型及尺寸由设计者根据分析的目的来设计^[17-18]。“探针”通过在待处理信号中不停移动来分析各部分之间的联系，从而提取出有价值的信息进行结构描述^[19]。近年来，随着形态学理论的发展，形态学滤波被逐步推广到一维信号处理领域^[20-22]。在此，本文作者针对矿集区大地电磁强干扰的特征，讨论广义形态滤波器的优势，构建组合广义形态滤波器在时间域对大地电磁强干扰进行噪声压制，并给出基于组合广义形态滤波的大地电磁资料处理流程，在青海柴达木盆地开展相关试验研究，选取具有一定代表性的试验点进行组合广义形态滤波处理。

1  组合广义形态滤波

数学形态变换能将复杂的待处理信号与背景进行分离，并在拆解成若干个具有不同物理意义成分的同时，对信号本身所固有的主要特征及形状进行较好保持^[23-24]。对Maragos构建的经典形态开-闭和闭-开滤波器的统计特性进行研究可知，传统形态滤波器存在严重的统计偏倚现象^[25-26]。显然，单独使用传统的形态开-闭和闭-开滤波器不能达到理想的滤波效果。为了有效压制信号中的各种噪声干扰，可以在形态开、闭运算的级联过程中选用不同类型及尺寸的结构元 素构建广义形态滤波器，从而更好地克服统计偏倚现象^[27]。

1.1  广义形态滤波器的定义

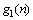设输入信号f(n)为定义在上的离散函数，结构元素为定义在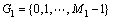上的离散函数，结构元素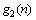为定义在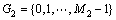上的离散函数，则f(n)关于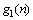和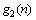的广义形态开-闭和形态闭-开滤波器定义为：

          (1)

          (2)

式中：和分别表示开运算和闭运算；g ₁和g ₂分别表示不同的结构元素；GOC为广义形态开-闭滤波器；GCO为广义形态闭-开滤波器。广义形态滤波器的基本滤波单元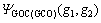定义为

        (3)

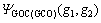式中：为形态滤波器的输出结果；为广义形态滤波器的基本滤波单元。利用广义形态开-闭和闭-开运算的线性组合，能较好地消除标准形态算子产生的统计偏倚现象，同时能保持目标信号所固有的几何结构特征，且不会模糊信号中突然出现的陡峭阶跃性变化。

图1所示为采用广义和传统形态滤波在消除统计偏倚现象上的仿真效果对比图。其中，原始信号假设为计算机模拟的4种不同幅值同一频率的正弦信号。

分析图1可知：传统形态开-闭和闭-开滤波器并没有完全滤除噪声，特别是在信号曲率最大的峰顶和谷底均有被削平的迹象。若待处理信号的能量增强、幅值增大，传统形态滤波在曲率变化处会出现极大失真现象，势必严重影响其噪声抑制能力。

图1  广义形态滤波消除统计偏倚现象效果图

Fig. 1  Effect charts of generalized morphological filter to eliminate statistical bias phenomenon

根据形态开、闭运算的收缩性及扩张性可知：开运算本身在消除正脉冲干扰的同时会加大负脉冲干扰，导致在形态开-闭滤波器中的闭运算若仍采用相同尺寸的结构元素，其输出结果将不能完全消除增强后的负脉冲干扰。从图1可知：有些负脉冲干扰仍然保留在传统形态开-闭滤波的结果中，而有些正脉冲干扰同样保留在传统形态闭-开滤波结果中。因此，由于传统形态滤波器选择相同类型及尺寸的结构元素，导致不能完全滤除正、负脉冲，而广义形态开-闭和闭-开滤波器由于选用不同类型及尺寸的结构元素，输出统计偏倚明显小于传统形态滤波器。经广义形态开-闭和闭-开滤波器处理后，在信号曲率变化处的细节成分得到了较好地保留，正、负脉冲均被较好地滤除，其整体去噪性能明显改善。

1.2  组合广义形态滤波器的构建

传统形态滤波虽可抑制正、负脉冲干扰，但由于仅采用相同类型及尺寸的结构元素，导致输出结果很难全面涉及信号在各个方向上的几何结构特征。因此，传统形态滤波在消除噪声干扰的同时，也丢失了信号中某些有用的局部细节信息，对处理过程中原始信号本身所固有的边缘特性及几何形状特征的保留产生不利影响。

广义形态滤波器的优势在于可以灵活选取不同类型和不同尺寸的结构元素，对消除传统形态滤波器存在的统计偏倚现象具有更好的效果，同时能有效提高对噪声干扰的压制性能。

传统形态开-闭(OC)和闭-开(CO)滤波器组成的并联平均基本滤波单元如图2所示，定义为。

由并联平均形态滤波单元组成常见的正、负结构元素广义形态滤波器和级联平均广义形态滤波器分别如图3和图4所示。

图2  并联平均基本滤波单元框图

Fig. 2  Block chart of parallel and average basic filter unit

图3  正、负结构元素广义形态滤波器框图

Fig. 3  Block chart of positive and negative structure element generalized morphological filter

图4  级联平均广义形态滤波器框图

Fig. 4  Block chart of cascade and average generalized morphological filter

考虑到大地电磁信号的准对称性及有效克服基线漂移现象，结合正、负结构元素和级联平均滤波器的优点构建如图5所示的组合广义形态滤波器，其目的是进一步抑制目标信号中的各种噪声干扰和消除统计偏倚现象^[28]。

由于圆盘型结构元素具有旋转不变性，避免了直线型结构元素平滑程度不够的缺点，同时，抛物线型结构元素能有效抑制脉冲噪声干扰，因此，结构元素选用圆盘型和抛物线型2种类型来设计组合广义形态滤波器。经组合广义形态滤波提取大地电磁强干扰的轮廓特征后，重构的大地电磁有用信号定义如下：

            (4)

1.3  时间域波形去噪效果

图6所示为一段实测大地电磁磁道H_x和H_y的时间域信号，经传统形态滤波和组合广义形态滤波处理后的去噪效果图。从图6可知，H_x和H_y的时域波形中均不同程度地受到典型大尺度强噪声的干扰。

分析图6可知：传统形态滤波在获取噪声轮廓上出现很严重的毛刺现象，曲线不光滑，连续性差，且在部分曲率最大处造成了信号的失真，滤波效果不好。这是由于传统形态开-闭和闭-开滤波器只采用单一类型及尺寸的结构元素进行处理，虽能在较大程度上压制了噪声，但信号的细节成分也被模糊化；组合广义形态滤波则几乎完整地勾勒出整段大尺度噪声轮廓，曲线自然、光滑，重构的大地电磁信号较好地保留了有用信号的细节信息，重现了原始大地电磁信号的基本特征，保持了目标信号的几何结构，从而保证了大地电磁有用信号的准确性。

2  基于组合广义形态滤波的大地电磁资料处理流程

图7所示为基于组合广义形态滤波的大地电磁资料处理流程。

首先，读取V5-2000大地电磁测深系统采集的原始数据，使其成为Window能识别的dat文件。然后，将3种不同采样率的E_x，E_y，H_x和H_y共12道信号分别进行组合广义形态滤波处理，结构元素的尺寸及大小由各道信号的波形特征决定。接着，将去噪处理后的dat数据重新还原成V5-2000格式的文件。最后，利用SSMT2000计算视电阻率和相位。

3  实际资料分析

为了验证组合广义形态滤波在大地电磁实测点中的噪声压制效果，在人烟稀少、基本无电磁干扰的青海省柴达木盆地开展了相关试验研究。试验主要是在大地电磁数据采集过程中，同时进行广域电磁法的数据采集，以广域电磁发射源作为人工干扰源，运用组合广义形态滤波对已知的伪随机干扰信号进行去噪，以未受到广域电磁发射源干扰的时间段信号作为评价标准，分析对比其去噪效果。

3.1  工区范围与测线分布

东坪MT采集概况：东坪构造位于青海省柴达木盆地西部阿尔金山前，为柴达木盆地西部坳陷区—里坪凹陷亚区的1个近南北走向三级背斜构造，行政区划隶属于青海省海西州。北靠阿尔金山南麓，构造西部与红山旱一号构造相接，南部与碱山构造相邻，东部与牛鼻子山梁构造相对。地表以砂泥质硬盐碱壳为主，地面海拔为2 770 m左右。地下为一近东西向展布，由北向南延伸至盆地的一个斜坡带，工区内整体地势较平坦。

图8所示为该工作区的范围与设计物探测线分布图。在东坪地区以东坪3井为中心，100 km²(即10 km×10 km)三维坐标布置5条广域电磁法测线，每条测线长为10 km，线距为2 km，点距为100 m。同时，在每条广域电磁法测线上布置11个大地电磁测点，点距为1 km，测网内共布置55个大地电磁测深点。

本次大地电磁数据采集的仪器使用的是4套V5-2000大地电磁测深系统，包括2台MTU-5A仪器(探头为MT8C-80)和2台MTU-5P仪器(探头为MTC-50)。为便于仪器的标记，对仪器进行了编号。

同时，为保证工作的准确及正常开展，首先对仪器盒子和磁棒进行标定，随后进行仪器一致性实验。

图5  正、负结构元素级联组合广义形态滤波器

Fig. 5  Combined generalized morphological filter of positive and negative structure element cascade

图6  传统和组合广义形态滤波效果对比

Fig. 6  Filtering effect comparison of traditional and combined generalized morphological filter

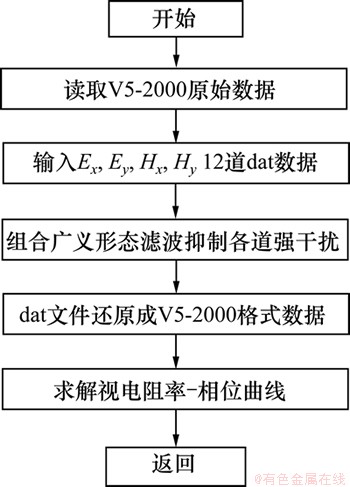
图7  基于组合广义形态滤波的大地电磁资料处理流程

Fig. 7  Magnetotelluric data processing procedure based on combined generalized morphological filter

野外布设采用“十”字型测量系统，电极采用不极化电极，保证极差在2 mV以内，电极距为170 m。使用森林罗盘测定方向，角度误差不超过0.5°。水平磁传感器离中心10 m左右呈正交地埋入地下20~30 cm处；垂直磁传感器垂直埋入地下，一般确保磁棒1/2~2/3长度被埋入地下。采集之前测量接地电阻，采取浇灌盐水、深挖电极坑、清除石块虚土和更换地点等措施确保接地电阻小于2 kΩ。在大地电磁采集开始前，规定沿测线方向(北偏东78°，近东西方向)为Y方向，与其垂直的方向为X方向(近南北方向)。

3.2  时间域信号分析

选用某测点作为试验点进行分析。该试验点具有以下特征：试验点采集时间为当天06:06到第二天凌晨01:10，共约19 h。其中，在06:06—07:36近1.5 h内，距该测点2 km远处的广域电磁发射机正在向地下注入电流为80 A的伪随机信号，频率范围为0.016~8 192 Hz，导致MT数据采集的同时也接收到广域电磁发射源的干扰；而在07:37—01:10近17.5 h内，由于广域电磁发射机停止工作，MT采集的数据未受其影响。

图9所示为该测点在06:06—07:36共1.5 h内的一段时间域波形。从图9可知：电道E_x和E_y以及磁道H_x和H_y中分别出现了大尺度类方波干扰和类充放电三角波干扰，其幅值和能量远大于正常大地电磁有用信号。观测整个干扰时间段的电道和磁道的时间序列发现，噪声干扰的类型均比较单一。因此，从时间域波形可以推断，该时间段受到的噪声干扰源应该也比较单一。

图10所示为该测点在07:37—01:10近17.5 h内的一段时间域波形。从图10可知：电道和磁道均未发现明显的非天然电磁场信号，即没有受到强噪声干扰。

对该测点的采集环境进行分析可知：该试验点周围地势平坦，在MT采集时除了广域电磁发射机在前1.5 h工作外，周围未发现其他明显的干扰源，因此，可以判断前1.5 h的MT采集信号中出现的大尺度异常波形应该是由广域电磁发射源所引起的。由于该测点仅受到广域电磁发射机的干扰，导致时间域波形中出现的干扰类型比较单一，主要体现为低频采样率时电道信号中出现的类方波干扰和磁道信号中出现的类充放电三角波干扰。

图8  工作区范围与设计物探测线分布图

Fig. 8  Workspace range and design geophysical exploration detecting line distribution

图9  含强干扰的一段时间域波形

Fig. 9  A period waveform of strong interference in the time domain

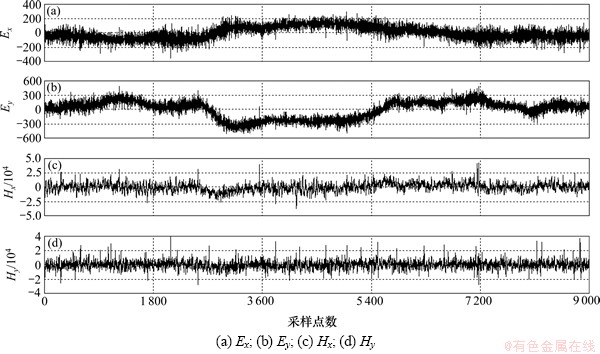
图10  未受噪声干扰的一段时间域波形

Fig. 10  A period waveform of unaffected strong interference in the time domain

图11所示为TS5格式采样(15 Hz)时，一段电道E_x分量数据采用组合广义形态滤波去噪前后的时间域波形。

图12所示为TS5采样率时，与图11相对应的同一时间段的磁道H_y分量数据经组合广义形态滤波去噪前后的时间域波形。

分析图11和图12可知：由于噪声干扰类型比较单一，电道E_x和磁道H_y中含大尺度的类方波干扰和类充放电三角波干扰经组合广义形态滤波处理后，较好地提取出了整个含强噪声干扰的轮廓曲线，重构信号基本还原了叠加在大尺度强干扰上非常微弱的大地电磁有用信号。

图11  E_x数据组合广义形态滤波去噪效果图

Fig. 11  Denoising effect chart of E_x data by combined generalized morphological filter

图12  H_y数据组合广义形态滤波去噪效果图

Fig. 12  Denoising effect chart of H_y data by combined generalized morphological filter

3.3  视电阻率-相位曲线

以均匀半空间的大地电磁场为例，视电阻率具体定义如下：

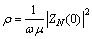               (5)

式中：为电阻率；为圆频率；为导磁率；；包括Z_TE和Z_TM，其中，Z_TE表示横电波型，Z_TM表示横磁波型，，。

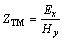式(5)表明：彼此正交的大地电场和磁场分量之比表示大地电磁阻抗张量。随着工作频率的降低，勘探深度会逐渐增加，在地面上测量得到的不同频率的阻抗可用来获取有关地下介质电阻率随深度变化的信息。由此可知，视电阻率反映的是在一定频率范围内，电磁场影响所能涉及岩石电性的综合情况。当频率不同时，电磁场影响的范围不同，视电阻率自然也随频率变化，反映的是对不同频率信号进行测量时，得到不同深度的电阻率。

考虑到组合广义形态滤波能较精确地提取出大尺度强噪声干扰的轮廓曲线，获取叠加在噪声轮廓上非常微弱的大地电磁信号。同时，由于试验点仅受到单一干扰源的影响，因此，可以运用组合广义形态滤波对该测点进行处理，并以未受到干扰时间段的大地电磁信号特征作为评价标准，说明该方法的有效性，具体步骤如下：首先，在时间域对受到干扰的时间段运用组合广义形态滤波去除大尺度强噪声干扰。然后，将重构后的大地电磁信号做阻抗估算，计算视电阻率-相位曲线。最后，与未受人工干扰时间段的视电阻率-相位曲线进行对比，说明去噪效果。

图13所示为广域电磁发射源干扰前后的视电阻率-相位曲线对比图。其中，未受到广域电磁发射源干扰时间段为07:37—01:10，受到广域电磁发射源干扰时间段为06:06—07:36。

分析图13(a)可知：该时间段的视电阻率曲线形态光滑、平稳，且数值稳定，相位曲线连续，呈50°左右。结合图10的时间域波形进行分析可以得出：该时间段由于未受到强噪声干扰，得到的视电阻率-相位曲线的形态特征符合正常逻辑。

分析图13(b)可知：xy方向的视电阻率曲线突跳明显；在0.1 Hz时，视电阻率下降至0.01Ω·m附近，而在0.05 Hz时，视电阻率上升至1Ω·m，相差近2个数量级，且该频段曲线不连续；yx方向的视电阻率曲线从1 Hz开始直线上升，直至0.005 Hz时，视电阻率达到最大值100Ω·m；xy方向的相位曲线在0.1 Hz附近不连续，频点凸变明显，且有误差棒；yx方向的相位曲线跳变剧烈，在1~0.005 Hz时几乎全为-180°。结合图9的时间域波形可知：由于该时间段受到了广域电磁发射机发射伪随机序列的干扰，导致低频段的数据质量严重下降，视电阻率-相位曲线形态紊乱。

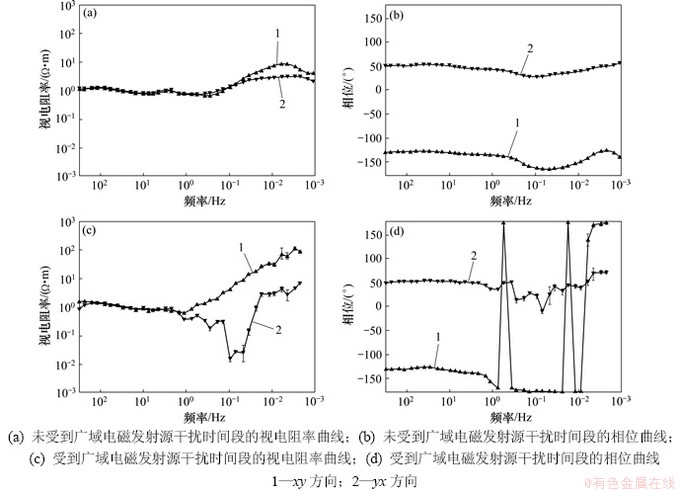
图13  广域电磁发射源干扰前后的视电阻率-相位曲线对比

Fig. 13  Comparison of apparent resistivity-phase curves by wide field electromagnetic interference source

从图13可知：由于噪声干扰持续时间仅为1.5 h，导致获得的视电阻率的频率范围有限，不足以反映该测点所包含的深部信息。

图14所示为该测点在受到广域电磁发射源干扰时间段(06:06—07:36)和全时段(06:06—01:10)的视电阻率-相位曲线对比结果。

分析图14可知：由于采集时间增长，大地电磁低频段延伸至0.001 Hz附近，中、低频段的数据质量也有所改善，但视电阻率曲线的整体形态仍然没有发生变化；xy方向的相位曲线在0.1 Hz附近仍出现凸跳现象，yx方向的相位曲线在1~0.01 Hz基本仍呈-180°。

由以上分析可知：由于广域电磁发射机工作的原因，该测点在前、后两段时间内视电阻率-相位曲线完全不同，因此，受广域电磁发射源干扰时间段的视电阻率-相位曲线已无法真实反映地下电性结构信息。对该试验点受到广域电磁发射源干扰时间段的E_x，E_y，H_x和H_y同时进行组合广义形态滤波处理。同时，为了确保获得的大地电磁频率能真实反映该测点深部的电性结构信息，将处理后的数据均在全时段进行阻抗估算。

图15所示为经组合广义形态滤波处理前后的全时段视电阻率-相位曲线对比图。分析图15可知：经组合广义形态滤波处理后，视电阻率-相位曲线得到了明显改善；除了xy方向的视电阻率-相位曲线在0.01~0.001 Hz处有个别频点蹦跳外，其他频段光滑、平稳，与未受到广域电磁发射源干扰时间段的视电阻率-相位曲线的整体形态(图13(a))非常相似，视电阻率也相对稳定。为更进一步与未受到广域电磁发射源干扰时间段的视电阻率-相位曲线进行比较，对图15(b)中部分飞点功率谱进行简单筛选。

图16所示为该测点在未受到广域电磁发射源干扰时间段和经组合广义形态滤波处理并进行功率谱筛选的全时段视电阻率-相位曲线对比图。

分析图16可知：经简单的功率谱筛选后得到的视电阻率-相位曲线光滑、连续，除了最后2个频点外， 其整体形态与未受到广域电磁发射源干扰时间段的曲线形态几乎完全一致。由于在不受干扰的情况下，同一测点在采集时间满足一定的勘探深度时，由不同时间段得到的电性结构应该是相同的，为此，通过上述试验，对受到噪声干扰的时间段进行处理，在全时段的整体形态上基本获得了未受到噪声干扰时间段的特征规律，从而证明了该方法的有效性和实用性。

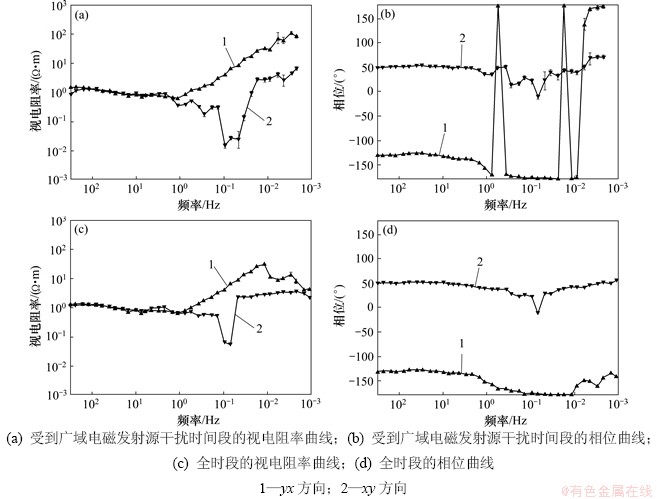
图14  受到广域电磁发射源干扰时间段和全时段的视电阻率-相位曲线对比

Fig. 14  Comparison of apparent resistivity-phase curves by wide field electromagnetic interference source time period and full time period

图15  全时段视电阻率-相位曲线对比

Fig. 15  Comparison of apparent resistivity-phase curves for full time period

图16  视电阻率-相位曲线对比

Fig. 16  Comparison of apparent resistivity-phase curves

以上试验结果表明：在时间域波形上，组合广义形态滤波可以更加精确地勾勒出大尺度强干扰的轮廓特征；视电阻率-相位曲线的整体形态更加光滑、平稳，与未受到广域电磁发射源干扰时的形态非常相似，除个别频点外无明显跳变，对功率谱略进行筛选即可基本达到未受人工干扰时的效果。因此，可以得出：当测点中所受的噪声干扰类型比较单一即噪声干扰源比较单一时，组合广义形态滤波具有较好的噪声抑制能力，受噪声污染的实测点的数据质量可以得到明显改善。

4  结论

(1) 由不同结构元素构建的广义形态滤波器其输出统计偏倚明显小于传统形态滤波器，有效地抑制了峰值和谷底的干扰信号，较好地保持了信号的几何结构特征，滤波性能得到了明显改善。

(2) 由正、负结构元素构建的组合广义形态滤波器，在时间域可以更加精确地勾勒出大尺度强噪声干扰的轮廓曲线，在曲率最大处也能较好地保留大地电磁有用信号的细节成分，基本还原了微弱的未受噪声干扰的大地电磁有用信号。

(3) 组合广义形态滤波对包含比较单一的强噪声干扰类型的测点具有较好的噪声抑制能力。经组合广义形态滤波处理后，受到广域电磁发射源干扰的时间段波形中基本剔除了大尺度干扰和基线漂移。视电阻率-相位曲线光滑、连续，与未受到广域电磁发射源干扰时间段的曲线形态非常相似，只需稍对功率谱进行筛选即可基本达到未受到干扰时的效果。

(4) 在实际应用中，结构元素类型和尺寸的选取对滤波的精度至关重要。针对具体的测点，需结合该测点采集时的具体环境、时域中所包含的干扰特征及不同采样率时受噪声干扰的程度来综合考虑及选取结构元素的类型及尺寸。若大尺度噪声干扰的轮廓提取不彻底，可能会损失部分有用信号的低频细节信息。

(5) 实际应用中结构元素类型和尺寸的选取对滤波的精度至关重要，针对具体的测点，需结合该测点采集时的具体环境、时域中所包含的干扰特征及不同采样率时受噪声干扰的程度来综合考虑及选取结构元素的类型及尺寸。另外，若大尺度噪声干扰的轮廓提取不彻底，可能会损失部分有用信号的低频细节信息。

参考文献：

[1] 董树文, 李廷栋, 高锐, 等. 地球深部探测国际发展与我国现状综述[J]. 地质学报, 2010, 84(6): 743-770.

DONG Shuwen, LI Tingdong, GAO Rui, et al. International progress in probing the Earth’s lithosphere and deep interior: A review[J]. Acta Geologica Sinica, 2010, 84(6): 743-770.

[2] 董树文, 李廷栋, 陈宣华, 等. 我国深部探测技术与实验研究进展综述[J]. 地球物理学报, 2012, 55(12): 3884-3901.

DONG Shuwen, LI Tingdong, CHEN Xuanhua, et al. Progress of deep exploration in mainland China: A review[J]. Chinese J Geophys, 2012, 55(12): 3884-3901.

[3] 董树文, 李廷栋, SinoProbe团队. 深部探测技术与实验研究(SinoProbe)[J]. 地球学报, 2011, 32(S1): 3-23.

DONG Shuwen, LI Tingdong, SinoProbe Team. Deep exploration technology and experimentation (SinoProbe)[J]. Acta Geoscientica Sinica, 2011, 32(S1): 3-23.

[4] Tikhonov A N. On determining electrical characteristics of the deep layers of the Earth’s crust[J]. Dok1 Akad Nauk SSSR, 1950, 73(2): 295-297.

[5] Cagniard L. Basic theory of the magnetotelluric method of geophysical prospecting[J]. Geophysics, 1953, 18(3): 605-635.

[6] 汤井田, 何继善. 可控源音频大地电磁法及其应用[M]. 长沙: 中南大学出版社, 2005: 1-6.

TANG Jingtian, HE Jishan. Controllable source audio magnetotelluric method and its application[M]. Changsha: Central South University Press, 2005: 1-6.

[7] 何继善. 可控源音频大地电磁法[M]. 长沙:中南大学出版社, 1990: 132-154.

HE Jishan. Controlled source audio frequency magnetotellurics [M]. Changsha: Central South University Press, 1990: 132-154.

[8] 吕庆田, 常印佛, SinoProbe-03项目组. 地壳结构与深部矿产资源立体探测技术实验—SinoProbe-03项目介绍[J]. 地球学报, 2011, 32(S1): 49-64.

L Qingtian, CHANG Yinfo, SinoProbe-03 Team. Crustal structure and three-dimensional deep exploration technology for mineral resources: An introduction to SinoProbe-03 Project[J]. Acta Geoscientica Sinica, 2011, 32(S1): 49-64.

[9] 吕庆田, 史大年, 汤井田, 等. 长江中下游成矿带及典型矿集区深部结构探测—SinoProbe-03年度进展综述[J]. 地球学报, 2011, 32(3): 257-268.

L Qingtian, SHI Danian, TANG Jingtian, et al. Probing on deep structure of middle and lower reaches of the Yangtze Metallogenic Belt and typical ore concentration area: A review of annual progress of SinoProbe-03[J]. Acta Geoscientica Sinica, 2011, 32(3): 257-268.

[10] 宋守根, 汤井田, 何继善. 小波分析与电磁测深中静态效应的识别、分离及压制[J]. 地球物理学报, 1995, 38(1): 120-128.

SONG Shougen, TANG Jingtian, HE Jishan. Wavelets analysis and the recognition, separation and removal of the static shift in electromagnetic soundings[J]. Chinese J Geophys, 1995, 38(1): 120-128.

[11] Sutamo D, Vozoff K. Phase-smoothed robust M-estimation of magnetotelluric impedance function[J]. Geophysics, 1991, 56(12): 1999-2007.

[12] 高静怀, 汪文秉, 朱光明. 小波变换与信号瞬时特征分析[J]. 地球物理学报, 1997, 40(6): 821-832.

GAO Jinghuai, WANG Wenbing, ZHU Guangming. Wavelet transform and instantaneous attributes analysis[J]. Chinese J Geophys, 1997, 40(6): 821-832.

[13] 汤井田, 化希瑞, 曹哲民, 等. Hilbert-Huang变换与大地电磁噪声压制[J]. 地球物理学报, 2008, 51(2): 603-610.

TANG Jingtian, HUA Xirui, CAO Zhemin, et al. Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data[J]. Chinese J Geophys, 2008, 51(2): 603-610.

[14] Cai J H, Tang J T. An analysis method for magnetotelluric data based on the Hilbert-Huang transform[J]. Exploration Geophysics, 2009, 40(2): 197-205.

[15] 汤井田, 徐志敏, 肖晓, 等. 庐枞矿集区大地电磁测深强噪声的影响规律[J]. 地球物理学报, 2012, 55(12): 4147-4159.

TANG Jingtian, XU Zhimin, XIAO Xiao, et al. Effect rules of strong noise on magnetotelluric (MT) sounding in the Luzong ore cluster area[J]. Chinese J Geophys, 2012, 55(12): 4147-4159.

[16] 朱威, 范翠松, 姚大为, 等. 矿集区大地电磁噪声场源分析及噪声特点[J]. 物探与化探, 2011, 35(5): 658-662.

ZHU Wei, FAN Cuisong, YAO Dawei, et al. Noise source analysis and noise characteristics study of MT in an ore concentration area[J]. Geophysical & Geochemical Exploration, 2011, 35(5): 658-662.

[17] 汤井田, 李晋, 肖晓, 等. 基于数学形态滤波的大地电磁强干扰分离方法[J]. 中南大学学报(自然科学版), 2012, 43(6): 2215-2221.

TANG Jingtian, LI Jin, XIAO Xiao, et al. Magnetotelluric sounding data strong interference separation method based on mathematical morphology filtering[J]. Journal of Central South University (Science and Technology), 2012, 43(6): 2215-2221.

[18] Li J, Tang J T, Xiao X. De-noising algorithm for magnetotelluric signal based on mathematical morphology filtering[J]. Noise and Vibration Worldwide, 2011, 42 (11): 65-72.

[19] Wang J, Xu G H, Zhang Q, et al. Application of improved morphological filter to the extraction of impulsive attenuation signals[J]. Mechanical Systems and Signal Processing, 2009, 23(1): 236-245.

[20] 赵静, 何正友, 钱清泉. 利用广义形态滤波与差分熵的电能质量扰动检测[J]. 中国电机工程学报, 2009, 29(7): 121-126.

ZHAO Jin, HE Zhengyou, QIAN Qingquan. Detection of power quality disturbances utilizing generalized morphological filter and difference entropy[J]. Proceedings of the CSEE, 2009, 29(7): 121-126.

[21] 陈辉, 郭科, 胡英. 数学形态学在地震信号处理中的应用研究[J]. 地球物理学进展, 2009, 24(6): 1995-2002.

CHEN Hui, GUO Ke, HU Ying. A study on application of mathematical morphology to seismic signal processing[J]. Progress in Geophys, 2009, 24(6): 1995-2002.

[22] Trahanias P E. An approach to QRS complex detection using mathematical morphology[J]. IEEE Transactions on Biomedical Engineering, 1993, 40(2): 201-205.

[23] 白银刚, 于盛林, 李建明. 一类新的广义形态开和广义形态闭滤波器[J]. 中国图像图形学报, 2009, 14(8): 1523-1529.

BAI Yingang, YU Shenglin, LI Jianming. A new generalized open and close Morphological filters[J]. Journal of Image and Graphics, 2009, 14(8): 1523-1529.

[24] 沈路, 周晓军, 张文斌, 等. 广义数学形态滤波器的旋转机械振动信号降噪[J]. 振动与冲击, 2009, 28(9): 70-73.

SHEN Lu, ZHOU Xiaojun, ZHANG Wenbin, et al. De-noising for vibration signals of a rotating machinery based on generalized mathematical morphological filter[J]. Journal of Vibration and Shock, 2009, 28(9): 70-73.

[25] Maragos P, Schafer R W. Morphological filters-Part Ⅰ: Their set theoretic analysis and relation to linear shift invariant filters[J]. EEE Transactions on Acoustics, Speech and Signal Processing, 1987, 35(8): 1153-1169.

[26] Maragos P, Schafer R W. Morphological filters-Part II: Their relation to median, order-statistic and stack filters[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1987, 35(8): 1170-1184.

[27] 张文斌, 杨辰龙, 周晓军. 形态滤波方法在振动信号降噪中的应用[J]. 浙江大学学报(工学版), 2009, 43(11): 2096-2099.

ZHANG Wenbin, YANG Chenlong, ZHOU Xiaojun. Application of morphology filtering method in vibration signal de-noising[J]. Journal of Zhejiang University (Engineering Science), 2009, 43(11): 2096-2099.

[28] 汤井田, 李晋, 肖晓, 等. 数学形态滤波与大地电磁噪声压制[J]. 地球物理学报, 2012, 55(5): 1784-1793.

TANG Jingtian, LI Jin, XIAO Xiao, et al. Mathematical morphology filtering and noise suppression of magnetotelluric sounding data[J]. Chinese J Geophys, 2012, 55(5): 1784-1793.

(编辑  陈灿华)

收稿日期：2013-06-25；修回日期：2013-08-19

基金项目：国家科技专项(SinoProbe-03)；国家自然科学基金资助项目(41104071)；湖南师范大学博士启动基金资助项目(130617)

通信作者：汤井田(1965-)，男，江苏连云港人，博士，教授，从事信号处理及电磁法数值模拟研究；电话：13507317396；E-mail: jttang@csu.edu.cn