基于矩阵重构的非圆信号ESPRIT算法
司伟建1，林晴晴1，张铁军2
(1. 哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨，150001；
2. 总参陆航部驻上海地区军事代表室，上海，200233)
摘要：在信号源为非圆信号的情况下，提出一种基于矩阵重构的ESPRIT波达方向估计方法。根据非圆信号为实值信号的特点，首先通过对接收数据矩阵进行共轭重排，构造多个具有旋转不变关系的子阵；为抑制噪声对算法的影响，对接收数据矩阵进行延迟处理，并构造其与各子阵之间的协方差矩阵；最后利用ESPRIT算法的原理实现信号波达方向的估计。仿真结果表明：在相同的信噪比和快拍数条件下，算法的正确分辨概率和测角精度均优于ESPRIT算法，并且在信号入射角度间隔较小时也具有良好的分辨性能。
关键词：波达方向；ESPRIT算法；非圆信号；数据矩阵重构
中图分类号：TN911.7 文献标志码：A 文章编号：1672-7207(2013)12-4936-06
ESPRIT algorithm for non-circular signals based on matrix reconstruction
SI Weijian1, LIN Qingqing1, ZHANG Tiejun2
(1. College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China;
2. Military Representative Office of the Army Aeronautical Department Resident in
Shanghai Region for the Headquarters of General Staff, Shanghai 200233, China)
Abstract: To estimate the direction-of-arrival (DOA) of non-circular signals, an estimation of signal parameters via rotational invariance techniques (ESPRIT) algorithm based on data matrix reconstruction was presented. Firstly, considering the properties of non-circular signals, sub-matrixes with rotational invariance relationship were conducted by conjugating and reconstructing the received data. In order to restrain the interference of noise, we delayed the received data matrix, and conducted the covariance matrixes between sub-matrixes and the delayed received data matrix. At last, the DOAs of signals were estimated by ESPRIT algorithm. Simulation results show that the resolution performance and angular precision of the proposed algorithm are better than those of ESPRIT algorithm under the same signal to noise ratio (SNR), and it has better resolution performance at the condition of small angle spacing.
Key words: direction of arrival (DOA); estimation of signal parameters via rotational invariance techniques (ESPRIT) algorithm; non-circular signals; data matrix reconstruction
波达方向(direction of arrival, DOA)估计是阵列信号处理领域的一个重要研究方向，在雷达、声纳、通信及医学成像等领域有着广泛的应用。其中信号子空间类波达方向估计算法因其精确的角度估计和超分辨性能成为研究热点，例如多重信号分类(multiple signal classification, MUSIC)算法[1-3]和旋转不变子空间(estimation of signal parameters via rotational invariance techniques，ESPRIT)算法[4-5]。MUSIC算法利用接收数据协方差矩阵特征分解后得到的信号子空间和噪声子空间的正交性生成空间谱，但是需要进行谱峰搜索来确定信号的DOA，耗费了大量时间。ESPRIT算法[6-8]不需要进行谱峰搜索，而是根据子阵间的旋转不变性，利用不同方向的信号到达两子阵间的相位差不同，来估计信号的DOA。近年来，对在现代通信和卫星系统中常见的BPSK和MASK等非圆信号的波达方向估计的研究受到了国内外学者越来越多的关注。研究利用非圆信号的特征来提高波达方向估计的性能成为了阵列信号处理领域的一个研究热点，学者们提出了许多基于非圆信号的波达方向估计算法[9-13]。Tayem等[14]提出的C-SPRIT (Conjugate ESPRIT)算法通过对接收数据进行共轭重排巧妙的生成了2个具有旋转不变关系的子阵，通过对子阵进行处理得到了信号的DOA。史文涛等[15-16]将C-SPRIT算法的原理推广到了MUSIC算法中，但是MUSIC算法需要进行谱峰搜索，耗费了大量的时间。本文作者利用非圆信号为实值信号的特点，提出了基于矩阵重构的非圆信号ESPRIT(Noncircular-CSPRIT)算法，通过对接收数据矩阵进行共轭重排，构造了阵列结构相同并且相邻子阵间存在旋转不变关系的子阵，子阵个数与阵元个数相同，对接收数据的利用更加充分；然后对接收数据矩阵延迟处理并与子阵构造新的协方差矩阵，很好的抑制了噪声对算法的影响；最后利用ESPRIT算法的原理实现了信号DOA的估计。
1 信号模型
考虑有1个由M个全向阵元组成的等距均匀线阵，假设有D个不相关的窄带信号分别从角度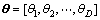
由远场入射到该天线阵列，阵元间距d等于入射信号的半波长。在t时刻第m个(m=1，2，…，M)阵元的接收信号为：
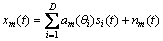(1)
其中：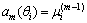
为第m个阵元在方向θi上的导向系数，
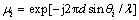，λ为入射信号波长。
阵列接收数据的表达式为
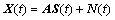(2)
式中：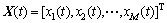
为M×1维的阵列接收数据矩阵；上标T表示对矩阵进行转置；
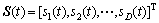为D×1维的信号矢量矩阵；
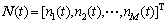为M×1维的噪声矢量矩阵，N(t)为零均值的加性高斯白噪声，各阵元输出噪声统计独立并且与信号相互独立；
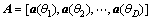为M×D维的导向矢量阵，其中
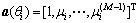表示阵列在θi方向的导向矢量。
因此接收数据的协方差矩阵为：
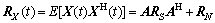(3)
其中：上标H表示对矩阵进行共轭转置，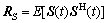
为信号协方差矩阵，
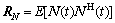为噪声协方差矩阵。
2 算法原理
2.1 C-SPRIT算法
Tayem等[14]提出的C-SPRIT算法，通过对接收数据矩阵进行共轭重排来获得2个具有旋转不变关系的子阵，然后利用ESPRIT算法的原理进行DOA估计，如图1所示。
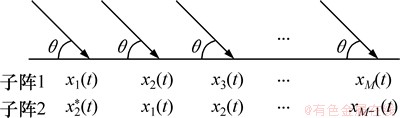
图1 C-SPRIT算法的数据输出
Fig. 1 Output data of C-SPRIT algorithm
子阵1的阵列输出为
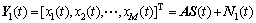(4)
子阵2的阵列输出为
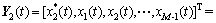
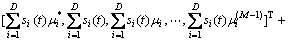
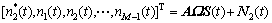(5)
这里信号为非圆信号，假设信号包络为实包络，对于像BPSK和MASK这样的信号有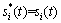
。
其中：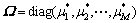
为对角阵，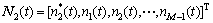
为经过共轭重排处理后的噪声矢量矩阵。
经过对数据进行共轭重排后得到了子阵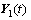
和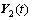
，两者的阵列结构相同且存在着阵列间距
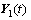，包含了入射角度信息。也就是说子阵和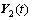构成了移动不变矩阵对，因此可以利用ESPRIT算法的原理对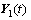和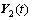进行处理得到包含入射信号角度信息的对角阵。这就是C-SPRIT算法的原理。
2.2 Noncircular- CSPRIT算法原理
2.2.1 数据共轭重构
C-SPRIT算法将数据进行一次共轭重排后得到子阵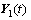和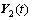，仅构造了一个旋转不变阵，为了更加充分的利用共轭重排的数据，这里将所有数据进行共轭重排，得到M个子阵，，…，
。
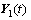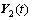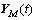因此，第3个子阵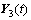
为：
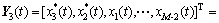
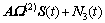(6)
其中：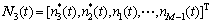
。
以此类推，第m个(m=1，2，…，M)子阵Ym(t)为
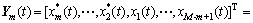
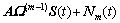(7)
其中：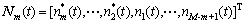
。
2.2.2 噪声的抑制
传统的DOA估计算法要求噪声在空间上是不相关的，协方差矩阵的计算只利用了零延迟相关函数，而忽略了非零延迟相关函数中隐藏的信号入射角度信息。为了利用非零延迟相关函数中的信息，本文构造阵列接收数据X(t)的第k个阵元xk(t)和的第l个阵元xl(t)之间的延迟相关函数为：
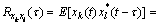
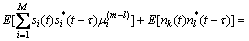
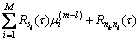(8)
其中：延迟τ＞0，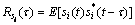
为入射信号si(t)的延迟自相关函数；
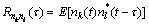为第k个与第l个阵元接收噪声之间的延迟互相关函数。
分析式(8)的延迟相关函数，当存在延迟τ时，对于窄带入射信号，在时间τ内可以忽略包络的变化。而对于方差为σ2的加性高斯白噪声，不同阵列之间的噪声经过时间τ的延迟后，噪声之间不再具有相关性，因此式(8)中信号和噪声是可分离的。
而在实际工程应用中，信号在时间上是相关的。当接收机带宽较宽时，噪声的功率谱近似为一条直线，因此噪声的时间相关长度远小于信号的时间相关长度，也就是说在时间上可以认为噪声是不相关的，信号与噪声在时间上存在一个可分离性，因此可以令延迟τ远小于入射信号带宽的倒数。因此有
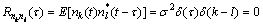(9)
即当2个阵元数据存在一定的延迟τ时，它们的延迟相关函数的噪声项为零，式(8)可写成
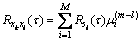(10)
因此，可以通过对数据进行延迟相关处理来有效的抑制噪声。
2.2.3 DOA估计
对阵列接收数据X(t)进行时间长度为τ的延迟
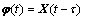(11)
根据2.2.2节对噪声的抑制原理，构造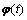
与共轭重排得到的M个子阵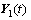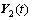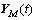，，…，之间的协方差矩阵为：
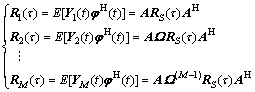(12)
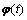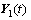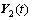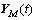由式(12)可知：与子阵，，…，之间的相关矩阵
，
，…，
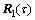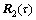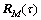有效地抑制了噪声的影响，各相关矩阵的阵列结构相同并且相邻相关矩阵构成了移动不变矩阵对，这就可以利用ESPRIT算法的原理对M个相关矩阵进行处理得到包含入射信号角度信息的对角阵，进而实现DOA估计。
令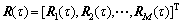
，对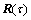
进行奇异值分解，求出奇异值构成的对角阵以及对应的左奇异矢量和右奇异矢量构造的矩阵U和V。将奇异值由大到小进行排列，其中前D个大的奇异值对应的左奇异矢量构成的矩阵即为信号子空间
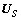，并且有
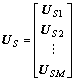(13)
其中：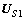
，
，…，
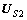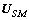都是M×D维的，它们和矩阵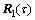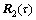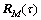，，…，的方向矢量张成的子空间为同一个空间，因此存在一个非奇异矩阵T，使得
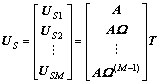(14)
由式(14)可以推得
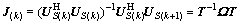(15)
其中：k=1，2，…，M-1。
对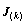
进行特征值分解即可得到对角阵，进而得到μi(i=1，2，…，D)，因此入射信号的角度信息为
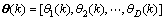(16)
其中：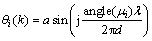
，i=1，…，D。
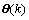为通过对第k个信号子空间
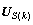与第k+1个信号子空间
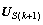进行处理得到的信号的DOA，利用平均的思想，对M-1对相邻的信号子空间进行处理得到的入射信号DOA求取平均得
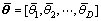(17)
其中：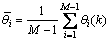
。
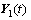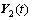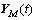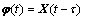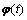本文算法估计入射信号的DOA，首先通过对阵列接收数据X(t)进行M次共轭重排，得到M个子阵，，…，，这M个子阵的阵列结构相同并且相邻子阵间存在一个旋转不变关系。然后对X(t)进行延迟得到，最后构造与子阵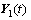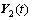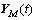，，…，之间的相关矩阵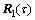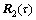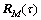，，…，，这样处理得到的相关矩阵很好地抑制了噪声的影响，进而可以提高算法的估计性能。
3 仿真分析
为了验证本文提出Noncircular-CSPRIT算法的性能，将Noncircular-CSPRIT算法与传统的ESPRIT算法和Tayem等[14]提出的C-SPRIT算法的性能进行比较。仿真实验采用七元均匀线阵，阵元间距为半波长，采用不相关的BPSK信号，系统噪声为加性高斯白噪声。本文使用的正确分辨概率定义为正确估计DOA的次数与实验次数的比值，均方根误差(root mean square error, RMSE)定义为：
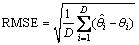(18)
其中：D为信号个数；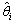
和
分别为第i个信号入射角度的估计值与理论值。
3.1 信噪比对算法性能的影响
3个BPSK信号入射到该天线阵，快拍数取100，在不同的信噪比(signal to noise ratio, SNR)下进行100次Monte Carlo实验，统计3种算法的正确分辨概率与均方根误差，结果如图2和3所示。
由图2和3可知：随着信噪比的增大，3种算法的正确分辨概率提高、均方根误差减小，算法的性能提高。在快拍数为100时，Noncircular-CSPRIT算法的ESPRIT算法和C-SPRIT算法正确检测概率为100%时的信噪比门限分别为7，9和10 dB；均方根误差小于1°时的信噪比门限分别为-4，-2和-2 dB，即在相同的信噪比下本文算法相对于其他2种算法性能最优。
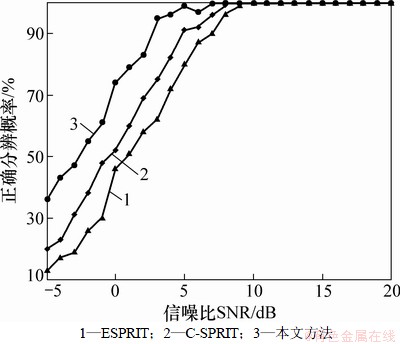
图2 正确分辨概率与信噪比的关系
Fig. 2 Relationships between resolution probability and SNR
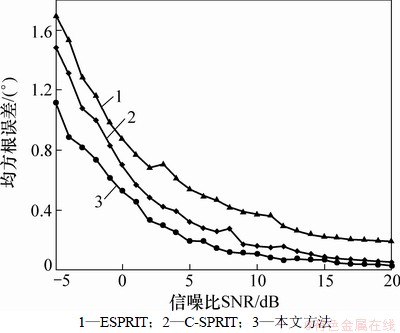
图3 均方根误差与信噪比的关系
Fig. 3 Relationships between RMSE and SNR
3.2 快拍数对算法性能的影响
3个BPSK信号入射到该天线阵，信噪比SNR=13 dB，在不同的快拍数下进行100次Monte Carlo实验，统计3种算法的正确分辨概率与均方根误差，结果如图4和5所示。
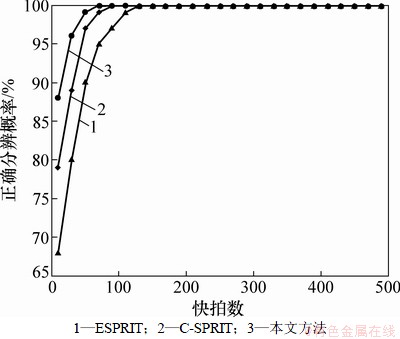
图4 正确分辨概率与快拍数的关系
Fig. 4 Relationships between resolution probability and number of snapshots
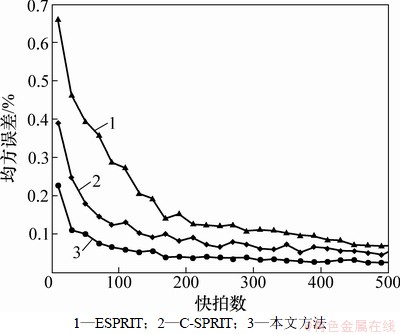
图5 均方根误差与快拍数的关系
Fig. 5 Relationships between RMSE and number of snapshots
由图4和5可知：随着快拍数的增大，3种算法的正确分辨概率提高、均方根误差减小，算法的性能提高。在信噪比为13 dB时，Noncircular-CSPRIT算法的ESPRIT算法和C-SPRIT算法正确检测概率为100%时的最小快拍数分别为40，50和70，在相同的快拍数条件下本文算法相对于其他2种算法性能最优，并且本文算法在小快拍数下也具有较好的分辨性能。
3.3 小角度间隔下的算法性能
采用2个BPSK信号，信号入射角度分别为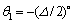
，
，
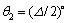表示2个信号的角度间隔，即为分辨力，令信噪比SNR=13 dB，快拍数为100，进行100次Monte Carlo实验，统计3种算法的正确分辨概率与均方根误差，结果如图6和7所示。
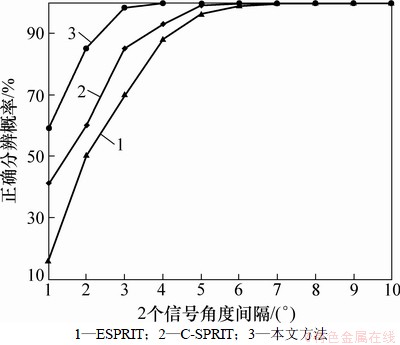
图6 不同角度间隔下的正确分辨概率
Fig. 6 Resolution probability of different angle interval
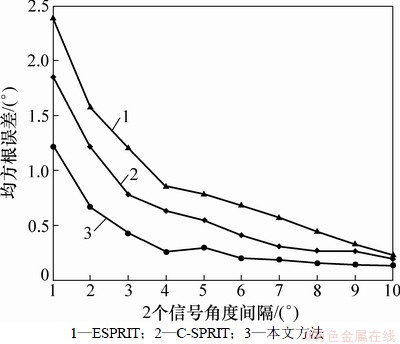
图7 不同角度间隔下的均方根误差
Fig. 7 RMSE of different angle interval
图6和7给出了2个信号入射时，不同角度间隔下的算法性能。随着2个信号的角度间隔的增大，3种算法的性能均有提高。Noncircular-CSPRIT算法的ESPRIT算法和C-SPRIT算法在2个信号的入射角度间隔至少为4°，6°和7°时，正确检测概率为100%，并且在小角度间隔下本文算法的DOA估计精度最高。
图2~7的结果表明了本文提出的Noncircular-CSPRIT算法的分辨性能相对于ESPRIT算法和C-SPRIT算法均有提高。这是因为文献提出的C-SPRIT算法仅对接收数据进行了一次共轭重排，生成了2个子阵，然后利用ESPRIT算法的原理进行DOA估计。而Noncircular-CSPRIT算法对接收数据进行了M次的共轭重排，从而生成了M个具有旋转不变关系的子阵，对数据的利用率得到了提高，并且通过数据的进行延迟相关处理很好的抑制了噪声对算法的影响，因此本文算法的性能得到了提高。
4 结论
(1) 提出的Noncircular-CSPRIT算法通过构造阵列结构相同并且相邻子阵间存在旋转不变关系的子阵，对接收数据矩阵延迟处理并与子阵构造新的协方差矩阵，很好地抑制了噪声对算法的影响，进而可以提高DOA估计的精度和分辨力。
(2) 在相同的信噪比和快拍数条件下，Noncircular-CSPRIT算法正确检测概率达到100%的信噪比和快拍数门限均低于ESPRIT算法及C-SPRIT算法，并且DOA估计精度高于2种算法的估计精度，本文算法性能最优。
(3) 在2个入射信号角度间隔不小于4°时，Noncircular-CSPRIT算法可以分辨2个信号，而ESPRIT算法及C-SPRIT算法分别需要2个信号的角度间隔至少为6°和7°，本文算法在小角度间隔下也具有良好的分辨性能。
参考文献：
[1] Le Bihan N, Miron S, Mars J I. MUSIC algorithm for vector-sensors array using biquaternions[J]. IEEE Transactions on Signal Processing, 2007, 55(9): 4523-4533.
[2] Chevalier P, Ferreol A, Albera L. High-resolution direction finding from higher order statistics: The 2q-MUSIC algorithm[J]. IEEE Transactions on Signal Processing, 2006, 54(8): 2986-2997.
[3] LIANG Junli, LIU Ding. Passive localization of mixed near-field and far-field sources using two-stage MUSIC algorithm[J]. IEEE Transactions on Signal Processing, 2010, 58(1): 108-120.
[4] Ottersten B, Kailath T. Direction-of-arrival estimation for wide-band signals using the ESPRIT algorithm[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1990, 3(2): 317-327.
[5] LI Jian, Compton R T Jr. Two-dimensional angle and polarization estimation using the ESPRIT algorithm[J]. IEEE Transactions on Antennas and Propagation, 1992, 40(5): 550-555.
[6] Taillefer E, Hirata A, Ohira T. Reactance-domain ESPRIT algorithm for a hexagonally shaped seven-element ESPAR antenna[J]. IEEE Transactions on Antennas and Propagation, 2005, 53(11): 3486-3495.
[7] Sanguinetti L, Morelli M, Poor H V. An ESPRIT-based approach for initial ranging in OFDMA systems[J]. IEEE Transactions on Communications, 2009, 57(11): 3225-3229.
[8] ZHANG Xiaofei, GAO Xin, XU Dazhuan. Multi-invariance ESPRIT-based blind DOA estimation for MC-CDMA with an antenna array[J]. IEEE Transactions on Vehicular Technology, 2009, 58(8): 4686-4690.
[9] 郑春弟, 冯大政, 周祎, 等. 基于非圆信号的实值ESPRIT算法[J]. 电子与信息学报, 2008, 30(1): 130-133.
ZHENG Chundi, FENG Dazheng, ZHOU Yi, et al. A real-value algorithm of ESPRIT via exploitation of non-circular sources property[J]. Journal of Electronics and Information Technology, 2008, 30(1): 130-133.
[10] 刘剑, 黄知涛, 周一宇. 基于四阶累积量的非圆信号测向方法[J]. 电子与信息学报, 2008, 30(4): 876-880.
LIU Jian, HUANG Zhitao, ZHOU Yiyu. A new forth-order direction finding algorithm for noncircular signals[J]. Journal of Electronics and Information Technology, 2008, 30(4): 876-880.
[11] Abeida H, Delmas J P. Statistical performance of MUSIC-like algorithms in resolving noncircular sources[J]. IEEE Transactions on Signal Processing, 2008, 56(9): 4317-4329.
[12] GAO Feifei, Nallanathan A, WANG Yide. Improved MUSIC under the coexistence of both circular and noncircular sources[J]. IEEE Transactions on Signal Processing, 2008, 56(7): 3033-3038.
[13] Hassen S B, Bellili F, Samet A, et al. DOA estimation of temporally and spatially correlated narrowband noncircular sources in spatially correlated white noise[J]. IEEE Transactions on Signal Processing, 2011, 59(9): 4108-4121.
[14] Tayem N, Kwon H M. Conjugate ESPRIT (C-SPRIT)[J]. IEEE Transactions on Antennas and Propagation, 2004, 52(10): 2618-2624.
[15] 史文涛, 黄建国, 侯云山. 基于非圆信号的波束域共轭MUSIC方法[J]. 系统工程与电子技术, 2009, 31(10): 2317-2319.
SHI Wentao, HUANG Jianguo, HOU Yunshan. Beamspace conjugate MUSIC algorithm for non-circular signals[J]. Systems Engineering and Electronics, 2009, 31(10): 2317-2319.
[16] 史文涛, 黄建国, 侯云山. 基于非圆信号的MIMO阵列方位估计方法[J]. 系统工程与电子技术, 2010, 32(8): 1596-1599.
SHI Wentao, HUANG Jianguo, HOU Yunshan. DOA estimation method for MIMO array based on non-circular signals[J]. Systems Engineering and Electronics, 2010, 32(8): 1596-1599.
(编辑 陈爱华)
收稿日期：2013-03-14；修回日期：2013-06-09
基金项目：中央高校基本科研业务费重点专项资金项目(HEUCFZ1215)
通信作者：林晴晴(1987-)，女，山东济宁人，博士研究生，从事宽带信号处理、检测与识别及高分辨高精度测向技术研究；电话：18911717656；E-mail：linqinglqq@163.com
