J. Cent. South Univ. (2012) 19: 2458-2467 

DOI: 10.1007/s11771-012-1297-6

Analytical modeling and multi-objective optimization (MOO) of slippage for wheeled mobile robot (WMR) in rough terrain

O. A. Ani, XU He(徐贺), XUE Kai(薛开), LIU Shao-gang(刘少刚), ZHANG Zhen-yu(张振宇)

College of Mechanical and Electrical Engineering,Harbin Engineering University, Harbin 150001, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: Good understanding of relationship between parameters of vehicle, terrain and interaction at the interface is required to develop effective navigation and motion control algorithms for autonomous wheeled mobile robots (AWMR) in rough terrain. A model and analysis of relationship among wheel slippage (S), rotation angle (θ), sinkage (z) and wheel radius (r) are presented. It is found that wheel rotation angle, sinkage and radius have some influence on wheel slippage. A multi-objective optimization problem with slippage as utility function was formulated and solved in MATLAB. The results reveal the optimal values of wheel-terrain parameters required to achieve optimum slippage on dry sandy terrain. A method of slippage estimation for a five-wheeled mobile robot was presented through comparing the odometric measurements of the powered wheels with those of the fifth non-powered wheel. The experimental result shows that this method is feasible and can be used for online slippage estimation in a sandy terrain.

Key words: autonomous wheeled mobile robot; terramechanics; traction; motion control; soil shear failure; drawbar pull

1 Introduction

With the rapidly increasing application of wheel mobile robots in scientific planetary explorations, military, agriculture, rescue, forestry, industry and institutions, more and more attention is being paid to autonomous navigation in outdoor environments usually characterized by rough and uneven terrain. Accurate positioning and hence effective navigation and motion control of autonomous wheel mobile robots require that they are able to detect, accurately estimate and compensate for wheel slippage while traversing rough and deformable terrain. Accuracy of dead reckoning for wheeled mobile robot (WMR) positioning on rough terrain can be improved by compensating for rover-terrain dynamic effects such as wheel slippage, sinkage, and effective radius change due to compressive deformation. If these terrain effects are not taken care of, it can lead to incorrect position estimates [1].

Wheel slippage is defined as relative movement in the direction of travel at the mutual contact surface of traction or transport device and the surface, which supports it [2]. Wheel slippage can also be considered as the reduction in actual vehicle travel speed when compared to the theoretical speed that should be attained from the speed of the wheel. It has been noted that it may be undesirable or impossible to eliminate vehicle wheel slippage considering the fact that the maximum traction occurs at non-zero values of slip. However, there is need for the robot to be able to detect and estimate wheel slip at every point while traversing rough and deformable terrain so that adequate decision for motion control can be taken as it becomes necessary[3].

The wheel slip of a robot will occur when the traction force exceeds the maximum shear stress of the supporting terrain, leading to inability of the soil to support the stress and loose movement of the soil. This is in accordance with Coulomb-Mohr soil failure criterion which states that the soil will experience shearing failure when the force or load exerting on it exceeds its maximum shear stress. However, if this slip occurrence is undetected by the robot, it may result in the controller actuating the wheels to produce more torque, hence traction force, and this results in either sinkage or slip immobilization. This is a situation where the robot wheel begins to dig and sink into the soil or where the wheel rotation fails to produce corresponding forward motion in the direction of travel [4]. In Ref. [5] GUSTAFSSON reported a method of measuring vehicle wheel slip using encoders by comparing the speed of driven wheels to that of undriven ones and the relative difference in the wheel velocities of the two. This method was further cited in Ref. [6]. Taking odometer measurements from non-powered wheels enhances position estimation of autonomous field vehicles [7]. OJEDA and BORENSTEIN [8] proposed an odometry method that could provide good travel distance estimates as long as at least one wheel was gripping (that is the opposite of slipping). In this work, we present a precise concept of vehicle wheel slippage on rough and deformable terrain, with its modeling using the classical slip/traction mechanics and a method of slip estimation by comparing the odometric measurements of the powered wheels and the non powered fifth-wheel of a five-wheeled mobile robot platform. Also, this work tries to obtain the optimal wheel-terrain values required to achieve the optimum slippage in order to maximize the traction by formulating a multi-objective optimization problem and solving it in MATLAB. A precise estimation of the value of robot’s wheel slip will be useful for developing effective navigation algorithm and for motion control on rough and deformable terrain. The algorithm should have a decision point where the value of slip is compared to the optimum value required, hence initiating a signal to the controller to increase or reduce torque, change the direction of travel, or end the navigation.

2 A five-wheeled mobile robot with differential mechanisms

2.1 Overview of wheel robot

The robot platform (Fig. 1) used for this work consists of five wheels (rigid), with four powered and one having two sub wheels, one powered and the other unpowered.

Fig. 1 Picture of five-wheeled mobile robot

The prototype of the WMR (Fig. 2) [9] consists of a reconfigurable chassis. This implies that wheelbase, wheel stance, length of rocker, centre of gravity, vertical and horizontal stability margin, and caster/camber angles of wheels are adjustable, giving the rover an advantage of effective motion on rough and challenging terrain. These properties also facilitate adequate positioning of the rover for effective use of GPS signals, camera mast and other science equipment.

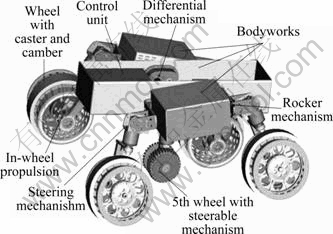
Fig. 2 Prototype of five-wheeled mobile robot showing some important parts

Each wheel can be adjusted around two pivots at the rocker mechanism, making the wheels produce forward and backward angles of inclination in the vertical plane as viewed from the side, like the caster of an automobile. Also, the wheels can be made to produce inside and outside angles of inclination in the cross vertical plane as viewed from the front, similar to a camber of an automobile. The steering mechanism is configured by HSR-5990TG robot servo and an unloading mechanism which absorbs the vibration from the interaction of wheel and terrain. The unloading mechanism contains Igus bearings, a rigid shaft and the bearing block among others.

2.2 Mechanism of the fifth wheel

The exploded view of the fifth wheel is shown in Fig. 3, indicating the major component parts. The fifth wheel consists of two sub wheels mounted on the either side of the wheel arm, with one sub wheel powered and the other unpowered [10].

Fig. 3 Exploded view of the fifth wheel

The bigger sub wheel which is the powered one is synchronized with the other four wheels and is controlled during motion through the program in the onboard industrial PC 104 computer with 90 mm × 90 mm dimension. The non-powered smaller fifth wheel has an encoder in it which measures the displacement of the robot supposedly at no slip situation.

3 Wheel slippage/traction modeling on rough terrain and optimization

3.1 Characteristics of rough terrain

SCHENKER et al [11] noted that although the subject of terramechanics has been studied for long time in other applications, it appears to be a fairly new research focus in rover design, for the reason of wide-ranging surface characteristics, the non-linear underlying wheel interactions, and empirical testing requirements. The missions of WMR for terrestrial applications as earlier highlighted most often require them to traverse through outdoor rough terrains. A terrain is described to be rough when it is characterized by any or all of the following items: irregular surface (with rocks and other materials of varying sizes and shapes), uneven (with different heights of obstacles, resulting in varying wheel contact angles), soft and deformable (with sand and fine textured soil) and having other surface cover different from the parent material of the terrain (e.g. plant materials, ice and snow) [3].

Generally, all these lead to low traction, rolling resistance, wheel slippage or travel reduction, wheel sinkage and finally energy and time loss. Figure 4 shows a typical natural rough terrain being traversed by FIDO rover [12].

Fig. 4 A typical natural rough terrain traversed by FIDO rover

3.2 Wheel slippage/traction modeling

Towards meeting the challenge of developing effective navigation and motion control algorithms for AWMR in rough terrain, IAGNEMMA et al [13] stated that advanced control and planning methods must be developed that consider the physical characteristics of the rover and its environment, and thus fully utilize the physical capabilities of the rover. A physics-based modeling technique for planetary exploration rovers operating in rough terrain was presented, as illustrated in Fig. 5. In this approach, both the rover and its environment are carefully modeled to ensure accurate prediction of the capabilities of the system.

Fig. 5 Physics-based modeling technique for AWMR in rough terrain

Three classes of parameters are important to adequately describe and model wheel-terrain interaction (Fig. 6). These include: vehicle/wheel parameters (e.g. input power, torque, and wheel characteristics like radius and width), terrain/soil parameters (e.g. shear stress, normal stress, coefficient of surface friction, soil cohesion, soil angle of internal friction, soil cohesive modulus, soil frictional modulus, soil bulk density, coefficients of wheel-soil interaction angles, shearing deformation, and soil sinkage exponent) and wheel-terrain interface/motion parameters (wheel slip, wheel sinkage, traction force, displacement of rover on terrain, time of travel of rover on terrain, wheel angular velocity, leading/entrance angle of wheel, trailing/departing angle of wheel, angle of maximum stress, slip angle, and wheel forward velocity). A good wheel-terrain interaction model should be able to connect key components of these three major classes of parameters.

Figure 7 shows a model of a rigid wheel on deformable terrain, where W is the vertical load on the wheel due to robot’s mass and P is horizontal pull force or drawbar pull, both applied by vehicle suspension on the wheel; T is torque applied by an actuator at the wheel rotation axis.

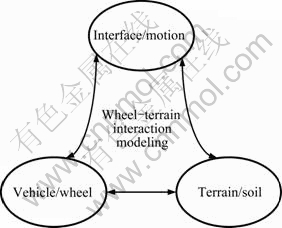
Fig. 6 Modeling of wheel-terrain interaction (traction)

Fig. 7  Model of a rigid wheel on deformable terrain

WONG [14] gave a relationship between the shear stress τ(θ) and the normal stress σ(θ) of loose soil beneath the wheel:

                         (1)

where c is the soil cohesion; φ is the soil internal friction angle; r is the wheel radius; k is the shear displacement under the wheel; S is the wheel slip; θ₁ is the angle between vertical and leading edge of wheel contact patch; θ is the rotation angle (angle between the vertical and normal stress).

In Fig. 7, θ₂ is the angle between the vertical and trailing edge of the wheel which is usually small and negligible [15].

The soil will fail, leading to slippage immobilization and sinkage when the shear stress exerting on the terrain by the wheel of the robot exceeds the maximum shear stress of the soil. The maximum shear stress τ_max is given by the Coulomb-Mohr soil failure criterion:

                        (2)

where σ_n(max) is the maximum normal stress.

The work of BEKKER [16-17] is one of the earliest works on slip and traction modeling which gives the fundamental idea that most researchers [18-24] in this field derive from. He showed the relationship between shear force and slip for different soils, and gave the model for soil shear/deformation using curves having the form of an over-damped sinusoid. However, JANOSI and HANAMOTO [22] proposed a simpler model that can be applied to most common soils and suggested that the shear stress τ and deformation j may be related as follows:

                       (3)

Given that k depends on soil properties, τ_max is obtained from Coulomb-Mohr soil failure criterion as earlier stated in Eq. (2).

The above mentioned works have treated other areas of wheel-terrain interaction like the relationship between torque and slip [22], between drawbar pull and slip [18] and friction coefficient and slip [20]; but not much has been done in analyzing the relationship between slip and wheel rotation angle, radius and sinkage together.

According to SAE in Ref. [22], vehicle wheel slip s is defined  as  the  relative  difference of  a  driven  wheel’s  circumferential  velocity  ωr and  its  absolute velocity ν, where r is the wheel radius.  Another common definition [25] is as follows:

,                     (4)

,                     (5)

And for small slip values, it has been noted that these definitions give almost the same answer.

In this work, wheel slip s is considered in the longitudinal direction with respect to the torque acting on it. In Eq. (6), which is another way of expressing vehicle wheel slip, v_a is the actual translational speed of (the centre of) the wheel; while v_t is the theoretical translational speed as determined from odometer measurements:

                                  (6)

From Eq. (1) and assuming the soil is completely dry (i.e. the effect of water content is negligible), let

                           (7)

This gives

           (8)

Dividing by T gives

 (9)

Opening the bracket gives

                  (10)

Simplifying further, we get

 (11)

    (12)

    (13)

For condition of non-zero value, dividing by (sinθ₁-sinθ) gives

                (14)

              (15)

(16)

In Eq. (1) and only for τ(θ), considering a particular case, when τ(θ)=τ(θ₁), this will imply that at this point also, θ=θ₁, and if this is substituted in Eq. (1), we have that τ(θ)=0 and Eq. (16) becomes

                     (17)

The wheel entrance angle θ₁ can be expressed as [26]

                            (18)

Equation (17) then becomes

           (19)

A numerical analysis of the changing tendencies of wheel radius, sinkage and rotation angle with slippage is carried out in a MATLAB simulation.

3.3 Multiobjective optimization (MOO)

3.3.1 Theory and application of MOO to AWMR motion control

An optimization problem is one requiring the determination of the optimal (maximum or minimum) value of a given function, called the objective function, subjected to certain defined restrictions, or constraints placed on the variables concerned [27]. Optimization could also be viewed as the process of making a decision or choosing the best out of available resources in order to achieve the most desired results [28]. In optimization problems, we are either interested in minimizing undesirable effects or maximizing desirable effects. The interest forms the objective of optimization from which the objective function is formulated. If the interest is one it is a single-objective optimization problem, but when the interest is two or more, then we have multi-objective optimization (MOO) problem. In this case of multi-objective optimization, the final solution of the objective functions will represent a compromise (trade-offs) between the different objectives which may be totally conflicting, partially conflicting or non-conflicting.

A general multi-objective minimization problem can be defined as

           (20)

where x is the element of decision variables bounded by the decision space, and f is the set of objectives to be minimized. The functions g(·) and h(·) are sets of inequality and equality constraints that define the feasible region of the n_x-dimensional continuous or discrete feasible solution space.

The MOO problems are mostly continuous and non- linear and the primary goal is to model a decision maker’s preferences, for instance, the ordering or relative importance of objectives of a wheel robot designer or that involved in developing motion control algorithm for autonomous wheeled mobile robots. From economics point of view, utility which is modeled with a function called utility function is a representation of the degree of satisfaction/contentment of the decision maker. The utility function is an amalgamation of the individual objective functions and is a mathematical expression that attempts to approximate the reference functions, which typically cannot be expressed in a single mathematical function or form.

In this work, the parameters to be analyzed and optimized are given in Eqs. (2), (7) and (19) for wheel slippage as the utility function F(x) depending on several variables expressed as x in the MOO problem formulation:

:

:

:

In order to obtain the optimal set of variables for minimum wheel slippage of the WMR, the fminimax algorithm in MATLAB is used. The utility function F(x) is given as

                 (21)

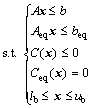
A solution is formulated in MATLAB as follows:

[x, f_n]=fminimax (@fun, x₀, A, b, A_eq, b_eq, l_b, u_b, @ C_non-linear, options…)                          (22)

where x=[r, z, θ, φ, c, kc, kφ, b, n]^T, is the optimal solution; A and b are linear inequality constraints specified by the matrix A and the vector b; A_eq and b_eq  are linear equality constraints specified by the matrix A_eq and the vector b_eq; l_b and u_b are lower and upper bounds on the variables specified as vectors; f_n is function that returns vectors; C_non-linear is the non linear constraint consisting of C and C_eq which are non linear inequalities and equalities respectively; “options” is the selective parameter for optimization; “fun” is the objective function to be minimized or maximized, i.e. f₁, f₂, f₃.

The choice of WMR and terrain parameters used in MOO and in the numerical simulation is based on the parameters of the 5-WMR considered in this work and characteristics of the selected soil/terrain type used in our test bed and available related information in literature (Table 1) [29].

Table 1 Parameters for various terrain types

3.3.2 Results of multi-objective optimization of wheel slippage for rigid wheel in deformable terrain

The results of multi-objective optimization of slippage for a rigid wheel moving in deformable terrain are presented in Table 2. The variables are nine in number and involve design variables such as wheel radius (r) and width (b); terrain characteristic variables such as cohesion (c), internal friction angle (φ), cohesion modulus (k_c), internal friction angle modulus (k_φ); and interface/running state variables such as wheel rotation angle (θ), sinkage (z) and sinkage exponent (n). This result reveals that to obtain the optimum wheel slippage determined as 0.114 6 for this particular WMR and terrain, the other variables should have the optimal values, as listed in Table 2. The MOO algorithm developed can be manipulated to suit the goal of the decision maker for design or motion control.

Table 2 Results of multiobjective optimization of wheel slippage

3.4 Simulation results

Numerical analysis and solution of Eq. (19) are presented in Figs. 8-10. Figures 8, 9 and 10 show the trend of changes of wheel slippage with respect to rotation angle, sinkage and wheel radius, respectively. These results reveal that these variables have some influence on wheel slippage.

4 Slip estimation with the fifth wheel

4.1 Method of estimation

Wheel slip of the five-wheeled mobile robot is to be estimated using Eq. (6) by comparing the velocity of the other four powered wheels with that of the fifth non- powered wheel. It is taken that the fifth wheel measures the circumferential velocity (same as theoretical velocity), and this is achieved through the embedded encoder pulse counts. The other four wheels also have encoders embedded in each of them which measure the actual velocity (i.e. when the wheels are experiencing slippage).

From Eq. (6), v_t is given as

                                    (23)

where ω is the angular velocity for the non-powered fifth wheel, and r is the radius of non-powered fifth wheel. An approximate formula for calculating ω is given as [9]

    (24)

where t_i-1, Δt_i-1, and ω_i-1 denote the start point, the width and the angular velocity corresponding to the (i-1)th pulse, respectively. Estimated slip can be applied in a motion control algorithm, as illustrated in Fig. 11.

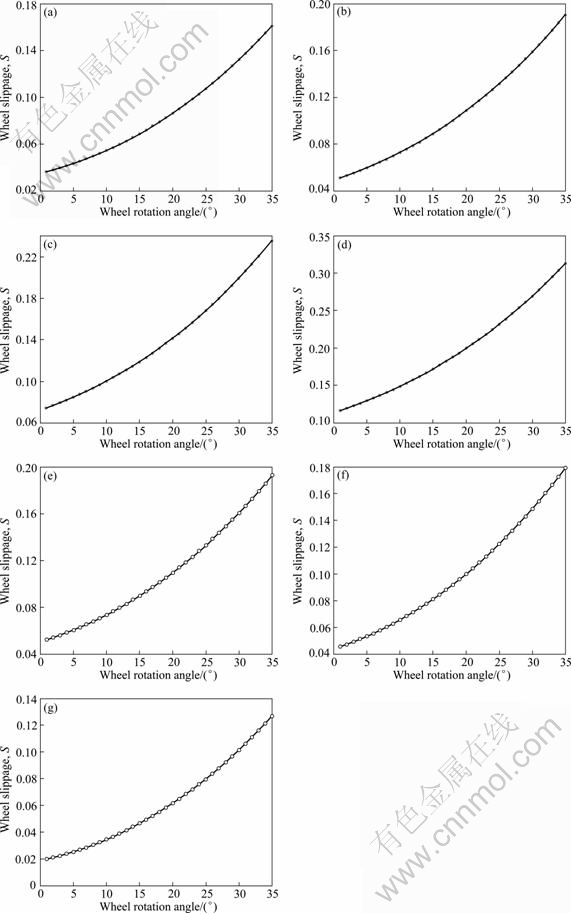
Fig. 8 Changing tendency of wheel slippage with rotation angle: (a) z=0.01 m, r=0.10 m; (b) z=0.014 m, r=0.10 m; (c) z=0.02 m, r=0.10 m; (d) z=0.03 m, r=0.10 m; (e) z=0.01 m, r=0.07 m; (f) z=0.01 m, r=0.08 m; (g) z=0.01 m, r=0.18 m

Fig. 9 Changing tendency of wheel slippage with sinkage (θ=32°): (a) r=0.07 m; (b) r=0.08 m; (c) r=0.10 m; (d) r=0.18 m

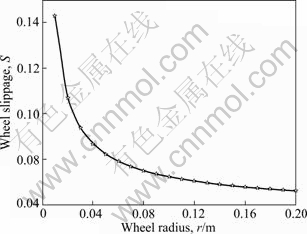
Fig. 10 Changing tendency of wheel slippage with radius (θ=32°, z=0.001 m)

4.2 Experimental result

The wheeled mobile robot was tested on a makeshift sandy terrain (Fig. 12) [30] and wheel slippage was estimated using the fifth wheel method. The result of slippage plotted against time is shown in Fig. 13. The range of slip shows covers for both driving and braking; however, slip exceeding 100% in either side is due to the influence of noise.

5 Discussion and application of results

Coulomb-Mohr soil failure criterion [31] is probably the most widely accepted model for predicting wheel slippage. However, the model does not contain slip as a variable in it; the prediction is usually inferred. The model infers that wheel slippage is a function of soil shear stress which in turn depends on normal stress, cohesion and angle of internal friction. SCREENIVASAN and WALDRON [32] stated that all wheel slippage is caused by soil characteristics, terrain inclination, load, vehicle configuration and kinematic incompatibility. The work of JANOSI and HANAMOTO [22] further confirms this idea when they tried to establish shear stress as a function of shear displacement in order to find the relationship between vehicle thrust and associated wheel slippage. This research work tries to develop a model for predicting wheel slippage based on the concept illustrated in Fig. 7, to find wheel slippage as a function of wheel rotation angle, wheel radius and sinkage. Wheel rotation angle depends on terrain inclination, soil characteristics and wheel configuration while sinkage depends on soil characteristics and load. This agrees with the ideas of other researchers already mentioned. This result could be applied in developing an online slippage detection and estimation algorithm for motion control of autonomous wheeled mobile robots with rigid wheels in deformable terrain. The rotation angle (θ) and entrance angle (θ₁) can be measured by visual camera or by kinematic analysis of the suspension of the wheel robot; while sinkage (z) can be measured by a high precision sliding resistance displacement sensor or through visual methods also by measuring the contact angle between the wheel and terrain using the geometrical relationship. The fifth wheel method can also be used for online slippage detection and estimation. Finally, the multi-objective optimization algorithm developed could be manipulated to suit the goal of a wheel robot designer or a person involved in developing motion control algorithm for autonomous wheeled mobile robots in rough terrain.

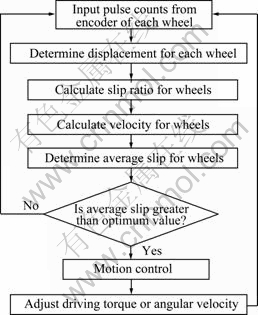
Fig. 11 Block diagram of slip estimation and motion control algorithm

Fig. 12 Picture of five-wheeled mobile robot being tested on makeshift sandy terrain

Fig. 13 Experimental result of slippage verses time by the fifth wheel method

6 Conclusion and future work

1) A model and an analysis of wheel slippage as a function of rotation angle, sinkage and wheel radius for a five-wheeled mobile robot moving in rough terrain are presented. The analysis is for a rigid wheel moving on a deformable and dry sandy terrain.

2) It is found that wheel slip is influenced by the rotation angle, sinkage and wheel radius. Wheel rotation angle depends on terrain inclination, soil characteristics and wheel configuration while sinkage depends on soil characteristics and load.

3) This result could be applied in developing an online slippage detection and estimation algorithm for motion control of autonomous wheeled mobile robots with rigid wheels in deformable terrain. The rotation angle (θ) and entrance angle (θ₁) can be measured by visual camera or by kinematic analysis of the suspension of the wheel robot; while sinkage (z) can be measured by a high precision sliding resistance displacement sensor or through visual methods also by measuring the contact angle between the wheel and terrain using the geometrical relationship. The fifth wheel method can also be used for online slippage detection and estimation.

4) The multi-objective optimization algorithm developed could be manipulated to suit the goal of a wheel robot designer or a person involved in developing motion control algorithm for autonomous wheeled mobile robots in rough terrain in order to maximize traction or minimize energy.

5) Future work will focus on sensor fusion approach (fifth wheel, IMU, and vision camera) to wheel slippage detection, estimation and compensation and online terrain parameter identification for motion control of autonomous wheeled mobile robots in rough terrain.

Acknowledgements

The authors are grateful to Dr. LIANG Ding of Harbin Institute of Technology, China, for making some of his relevant published papers available and for being available for useful discussion on them.

References

[1] FUKE Y, KROTKOV E. Dead reckoning for a lunar rover on uneven terrain [C]// Proceedings of IEEE International Conference on Robotics and Automation. Minneapolis, Minnesota, 1996: 411-416.

[2] ASAE-American Society of Agricultural Engineers. Uniform terminology for traction of agricultural tractors, self-propelled implements, and other traction and transport devices [M]. Agricultural Engineers Yearbook of Standards, 1983: 190-192.

[3] ANI O A, XU H, ZHAO G. Analysis and modelling of slip for a five-wheeled mobile robot (WMR) in an uneven terrain [C]// Proceedings of International Conference on Mechatronics and Automation (ICMA). Beijing, China, 2011: 154-159.

[4] YOSHIDA K, HAMANO H. Motion dynamics and control of a planetary rover with slip-based traction model [C]// Unmanned Ground Vehicle Technology IV. 2002: 275-286.

[5] GUSTAFSSON F. Slip-based tire-road friction estimation [J]. Automatica, 1997, 33: 1087-1099.

[6] IAGNEMMA K, WARD C C. Classification-based wheel slip detection and detector fusion for mobile robots on outdoor terrain [J]. Autonomous Robots, 2009, 26: 33-46.

[7] LINDGREN D R, HAGUE T, SMITH P J P, MARCHANT J A. Relating torque and slip in an odometric model for an autonomous agricultural vehicle [J]. Autonomous Robots, 2002, 13: 73-86.

[8] OJEDA L, BORENSTEIN J. Methods for the reduction of odometry errors in over-constrained mobile robots [J]. Autonomous Robots, 2004, 16: 273-286.

[9] XU H, TAN D, ZHANG Z, XUE K, JIN B. A reconfigurable mobile robot with 5th wheel [C]// Proceedings of the IEEE International Conference on Mechatronics and Automation. Changchun, China, 2009: 211-216.

[10] XU H, ZHANG Z, ALIPOUR K, XUE K, GAO X Z. Prototypes selection by multi-objective optimal design: Application to a reconfigurable robot in sandy terrain [J]. Industrial Robot: An International Journal, 2011, 38(6): 599-613.

[11] SCHENKER P, HUNTSBERGER T, PIRJANIAN P. Rovers for intelligent, agile traverse of challenging terrain [C]// International Conference on Advanced Robotics. Coimbra, Portugal: NASA Jet Propulsion Laboratory, 2003: 203-208.

[12] SAITOH K, MACHIDA T, KIYOKAWA K, TAKEMURA H. A 2D-3D integrated interface for mobile robot control using omnidirectional images and 3D geometric models. [C]// IEEE and ACM International Symposium on Mixed and Augmented Reality (ISMAR). Montreal, Canada: i-SAIRAS, 2007: 173-176.

[13] IAGNEMMA K, SHIBLY H, RZEPNIEWSKI A, DUBOWSKY S. Planning and control algorithms for enhanced rough-terrain rover mobility [C]// Proceedings of the Sixth International Symposium on Artificial Intelligence, Robotics and Automation in Space. i-SAIRAS. 2001.

[14] WONG J Y. Theory of ground vehicles [M] Third Ed, New York: John Willey and Sons, 2001: 144-153.

[15] THRUN S, BUECKEN A. Integrating grid-based and topological maps for mobile robot navigation [C]// Proceedings of 13th National Conference on Artificial Intelligence. Oregon, Poland, 1996: 944-950.

[16] BEKKER M G. Theory of land locomotion [EM/OL]. Ann Arbor, MI, University of Michigan Press, www.amazon.com/Theory- land-locomotion. 1956.

[17] BEKKER M G. Off-the-road locomotion [EM/OL]. University of Michigan Press, www.amazon.com ? Books ? Reference. 1960.

[18] REINA G. Methods for wheel slip and sinkage estimation in mobile robots [M]. Robot Localization and Map Building, 2006: 561-578.

[19] YOSHIDA K. Slip, traction control, and navigation of a lunar rover [C]// Proceeding of the 7th International Symposium on Artificial Intelligence, Robotics and Automation in Space. Nara, Japan, 2003: 1-7.

[20] IAGNEMMA K, GOLDA D, DUBOWSKY S. Experimental study of high-speed rough-terrain mobile robot models for reactive behaviours [C]// Proceedings of the 8th International Symposium on Experimental Robotics. Sant’ Angelo d’Ischia, Italy, 2002: 628-637.

[21] LINDGREN D R, HAGUE T, SMITH P J P, MARCHANT J A. Relating torque and slip in an odometric model for an autonomous agricultural vehicle [J]. Autonomous Robots, 2002, 13: 73-86.

[22] JANOSI Z, HANAMOTO B. The analytical determination of drawbar pull as a function of slip for tracked vehicles in deformable soils [C]// Proceedings of the 1st International Conference on Terrain-Vehicle Systems. Torino, 1961: 707-726.

[23] WONG J Y. Predicting the performances of rigid rover wheels on extraterrestrial surfaces based on test results obtained on earth [J]. J Terramechanics, 2012, 49(1): 49-61.

[24] HEMMAT A, NANKALI N, AGHILINATEGH N. Simulating stress-sinkage under a plate sinkage test using a viscoelastic 2D axisymmetric finite element soil model [J]. Soil & Tillage Research, 2012, 118: 107-116.

[25] GUSTAFSSON F. Slip-based tire-road friction estimation [J]. Automatica, 1997, 33: 1087-1099.

[26] DING L, GAO H, DENG Z, NAGATANI K, YOSHIDA K. Experimental study and analysis on driving wheel’s performance for planetary exploration rovers moving in deformable soil [J]. Journal of Terramechanics, 2011, 48: 27-45.

[27] STROUD K A. Advanced engineering mathematics [M]. Fourth Edition. Houndmills, Palgrave Macmillan, 2003: 940-948.

[28] CHI-KEONG G, KAY C T. Evolutionary multi-objective optimization in uncertain environments [M]. KACPRZYK J, Ed. Springer, 2009: 1-39.

[29] SHIBLY H, IAGNEMMA K, DUBOWSKY S. An equivalent soil mechanics formulation for rigid wheels in deformable terrain, with application to planetary exploration rovers [J]. Journal of Terramechanics, 2005, 42: 1-13.

[30] ZHANG Z. Kinematics and Estimation study on a rough terrain mobile robot [D]. Harbin Engineering University, 2011. (in Chinese)

[31] BEKKER M G. Theory of land locomotion [M]. Ann Arbor: University of Michigan Press, 1956.

[32] SREENIVASAN S, WALDRON K. Displacement analysis of an actively articulated wheeled vehicle configuration with extensions to motion planning on uneven surface [J]. J Mech Des, 1996, 118(2): 312-317.

(Edited by YANG Bing)

Foundation item: Project(60775060) supported by the National Natural Science Foundation of China; Project(F200801) supported by the Natural Science Foundation of Heilongjiang Province, China; Project(200802171053, 20102304110006) supported by the Specialized Research Fund for the Doctoral Program of Higher Education of China; Project(2012RFXXG059) supported by Harbin Science and Technology Innovation Talents Special Fund, China

Received date: 2011-12-12; Accepted date: 2012-04-24

Corresponding author: XU He, Professor; Tel: +86-13351117608; E-mail: railway_dragon@163.com