J. Cent. South Univ. Technol. (2010) 17: 549-553
DOI: 10.1007/s11771-010-0521-5 
Application of empirical mode decomposition in early diagnosis of
magnetic memory signal
LENG Jian-cheng(冷建成)1, 2, XU Min-qiang(徐敏强)1, ZHANG Jia-zhong(张嘉钟)1
1. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China;
2. Department of Mechanical Science and Engineering, Daqing Petroleum Institute, Daqing 163318, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract: In order to eliminate noise interference of metal magnetic memory signal in early diagnosis of stress concentration zones and metal defects, the empirical mode decomposition method combined with the magnetic field gradient characteristic was proposed. A compressive force periodically acting upon a casing pipe led to appreciable deformation, and magnetic signals were measured by a magnetic indicator TSC-1M-4. The raw magnetic memory signal was first decomposed into different intrinsic mode functions and a residue, and the magnetic field gradient distribution of the subsequent reconstructed signal was obtained. The experimental results show that the gradient around 350 mm represents the maximum value ignoring the marginal effect, and there is a good correlation between the real maximum field gradient and the stress concentration zone. The wavelet transform associated with envelop analysis also exhibits this gradient characteristic, indicating that the proposed method is effective for early identifying critical zones.
Key words: metal magnetic memory; noise interference; early diagnosis; empirical mode decomposition; magnetic field gradient; stress concentration; zones; envelop analysis
1 Introduction
Iron and steel are used widely in the construction of railways, bridges, airports, infrastructure, and buildings. So it is necessary and important to nondestructively inspect or monitor corrosion, cracks and other defects to ensure safety. Conventional nondestructive testing (NDT) techniques, such as magnetic particle inspection [1] and ultrasonic testing [2], only can detect already developed defects. So far, a new NDT method, referred to as metal magnetic memory (MMM) [3], has become an emerging field recently [4-9] because it has potentials in early diagnosis of fatigue damage and pre-defect state of metal.
MMM technique is based on the analysis of self-magnetic leakage field distribution on components’ surfaces for determination of stress concentration zones and metal defects [10]. Owing to unclear physical fundamentals of MMM method, many researchers have devoted their efforts to investigate variation regularities of MMM signals in laboratory. WILSON et al [4] measured magnetic field distributions under both applied and residual stresses, respectively, and obtained good correlation between them. DONG et al [5, 8] investigated the variation of stress-induced magnetic signals during static tensile test, and studied further different signal patterns due to elastic and plastic loads in tension and different signal characteristics at different cycles in fatigue tests for early damage assessment [7]. YANG et al [6] applied the magnetomechanical effect theory induced by cyclic tensile stress to interpret the relationship between surface magnetic field and elastic stress, and derived a simple model. LENG et al [9] discussed magnetic field variations throughout the rotary bending fatigue process and the corresponding signal characteristics to identify damage zones. The above laboratory studies focus on analyzing normal components of magnetic leakage fields, and the other basic diagnostic parameter is the magnetic field gradient on length which is rarely studied.
Indeed, the real signals measured in engineering practice usually contain interference noise. Since the magnetic memory signal is sensitive to noise, the stress concentration zones can hardly be distinguished directly, while the maximum gradient value has more advantages. Based on signal processing technique, the wavelet exponential denoising method and Hilbert transform [11-12] were introduced to analyze MMM signal, and signal-noise ratio was greatly improved. The signal singularity detection theory of wavelet transform was also employed to determine stress concentration zones [13], reducing the influence of noise. The above findings achieved good results, however, the effectiveness of wavelet denoising technique largely depends on the chosen wavelet basis function. Nevertheless, it is not easy to choose a suitable wavelet basis function that is not self-adaptive. In this work, empirical mode decomposition (EMD), a new time-frequency analysis method capable of self-adaptive filtering characteristic [14], was adopted to extract real gradient characteristics and accurately identify the stress concentration zones.
2 Introduction of empirical mode de- composition
EMD is a new signal decomposition method pioneered by HUANG et al [15]. It relies on data sifting according to the time scale that is defined as a time interval between successive extrema in the signal. A signal x will be decomposed into a finite number of n intrinsic mode functions (IMFs) ci, i=1, 2, …, n, similar to frequency bands of wavelet transform, which extract the energy associated with different intrinsic time scales and a residual r. Thus
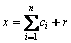(1)
where ci are different frequency bands arranged from high frequency to low frequency, and each component represents different physical properties because of self-adaptive decomposition. Hence, we can construct filters by choosing different IMFs.
The high-pass filter can be expressed as
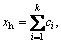i=1, 2, …, k (2)
where xh represents the first k IMFs, and thus high-frequency components of the signal are extracted effectively.
Similarly, the low-pass filter can be expressed as
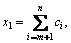i=m+1, m+2, …, n (3)
where xl represents the last (n-m) IMFs, and thus low-frequency components of the signal are extracted effectively.
Also, the band-pass filter can be expressed as
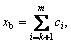i=k+1, k+2, …, m (4)
where xb represents the middle (m-k) IMFs, and thus middle-frequency components of the signal are extracted effectively.
From the above process, we can find that the signal is filtered in time domain, and there is no distortion during EMD. Thus, a new temporal space filtering method different from traditional filtering methods in frequency domain is constructed with the help of chosen IMFs. Consequently, the filtered signal can fully preserve intrinsic nonlinear and nonstationary characteristics of the signal itself. Since EMD algorithm is implemented based on local characteristics, it can give satisfactory results in analyzing physical measurements.
3 Experimental signal analysis
Nearly 40% accidental wells in complicated oil fields are induced by casing failure [11]. Bending, deformation or breaking easily occurs in casing pipes when subjected to unbalanced loads, thus reducing directly production efficiency and even abandoning the well. Therefore, it is of great significance to find stress concentration zones to avoid casing failure. Although MMM technique can be used to solve this problem, complex environments with high temperature, small space and bad noise in wells make serious stress concentration zones more difficult to be identified. In this work, the EMD method combined with the gradient characteristic was applied to analyzing the measurement signal.
The casing pipe of diameter of 140 mm and about 1 m in length studied was made of middle carbon steel. In this experiment, a compressive force of 160 kN to simulate squeezing action in the well was periodically acted around 350 mm on the casing pipe, and appreciable deformation appeared. The experimental system was photographically provided in the previous work [12]. The measurement surface was not preliminarily treated. The normal components of the magnetic field intensities, Hy, on the outer surface were collected at each 2 mm interval along the pipe length, L, by a magnetic indicator TSC-1M-4, with a scanning probe Type 2. Note that the sensor probe was always perpendicular to the surface with a lift-off of 2 mm during testing.
The measured data in the MM-system were exported to MATLAB software. The Hy distribution is plotted in Fig.1, and Fig.2 shows its absolute gradient values. It follows that the magnetic memory signal characteristic induced by stress concentration is not clear, confused by many extreme value zones. It is difficult to determine the real locations of stress concentration by virtue of the gradient characteristic of the raw signal alone since it is contaminated by several factors including measurement noise, imperfections in data collection and experimental error.
The original signal was decomposed into 11 IMFs and its residue with the help of the improved EMD [16],in which the first six IMFs are random noise with high frequency and low correlation coefficients less than 0.1. Fig.3 displays other IMFs containing useful information. It should be noted that the results of EMD with other measured data are quite similar, but the number of IMFs may differ slightly.
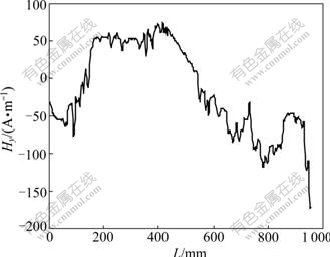
Fig.1 Magnetic memory signal collected from casing pipe
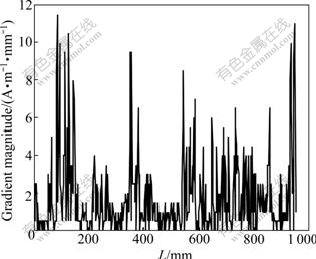
Fig.2 Absolute gradient curve of original signal
Based on the qualified correlation coefficients between the IMFs and the original signal, the above components, c7 to c11, are reconstructed as shown in Fig.4. Correspondingly, the absolute gradient curve is given in Fig.5. It is clear that the gradient around 350 mm represents the maximum value ignoring the marginal effect, corresponding to the stress concentration zone, which is in accordance with the real deformation location of the casing pipe. Notice that the gradient values around the margins, including from 0 to 100 mm, and 900 to 1 000 mm, are not considered due to the sudden variation in lift-off of the probe [12].
4 Discussion
Compared with the original measurement signal in Fig.1, it can be observed that the reconstructed signals in Fig.4 are purified and the correlation coefficient between them equals 0.956 4. As a result, the absolute gradient curve of the reconstructed signal definitely reveals that the maximum peak value is around 350 mm except the marginal effect at two ends, improving the accuracy for locating the stress concentration zone. Numerous experiments on measured data were carried out. Application results show that high-frequency noise can be filtered successfully by the EMD method, predicting the maximum gradient zones in correspondence with real damage locations.
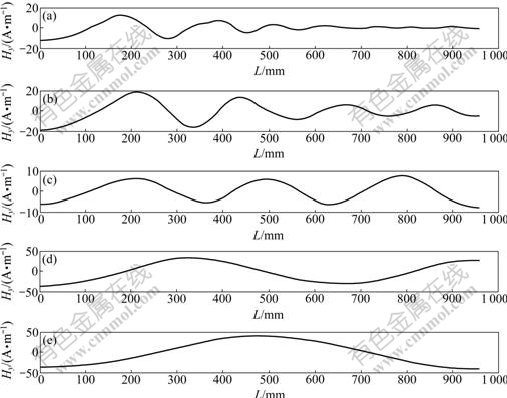
Fig.3 IMFs of lower frequency by EMD: (a) c7; (b) c8; (c) c9; (d) c10; (e) c11
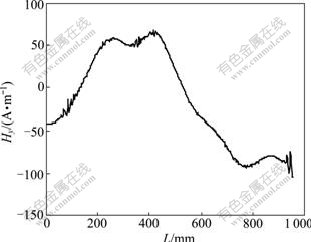
Fig.4 Reconstructed results of IMFs from c7 to c11
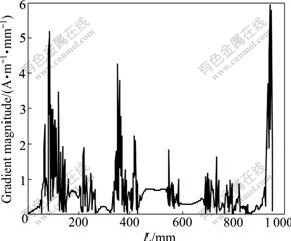
Fig.5 Absolute gradient curve corresponding to reconstructed signal in Fig.
In order to further verify the performance of the proposed method, the original signal was processed using the soft-thresholding wavelet denoising method. The subsequent envelop via Hilbert transform is shown in Fig.6. It can be seen that the amplitude around 350 mm
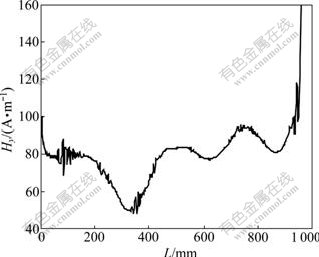
Fig.6 Envelop curve of denoised signal via wavelet transform
350 mm changes markedly, and the gradient curve also exhibits an absolute maximum value in this region as shown in Fig.7.
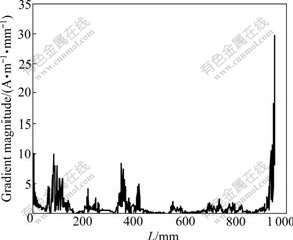
Fig.7 Absolute gradient curve of envelop
In general, although both wavelet transform and EMD method cannot solve the marginal effect of magnetic memory signal commendably, this problem can be ignored in engineering application. Due to self-adaptive denoising capability of EMD, it can effectively eliminate high-frequency noise, and give more distinct identification of real signal characteristic as compared to the wavelet transform.
5 Conclusions
(1) MMM technique is an effective method in early diagnosing structural failure or fatigue damage, and the maximum field gradient value has a good correlation with stress concentration zones, which can be used as a characteristic quantity.
(2) Since real MMM signals always contain much interference noise, denoising is required. Based on the self-adaptive filtering characteristics of EMD, the real maximum field gradient is successfully extracted.
(3) Compared with the wavelet transform, EMD has the same or even better denoising effect, simultaneously overcoming the difficulty of selecting basis functions.
(4) It is very important to predict abnormal stress concentration zones to avoid casing failure in oil fields, especially in complex working environments. The proposed method in this work provides a new way to diagnose casing faults in advance.
Acknowledgement
The authors are grateful to Dr. ZHANG Jun (Institute of Shanghai Academy of Spaceflight Technology, China) for providing the data analyzed in this work.
References
[1] PRESTON C R. Magnetic particle inspection of precipitation hardening type steels [J]. Insight, 2002, 44(12): 782-785.
[2] LERNER Y, BRESTEL P. Ultrasonic testing predicts casting properties [J]. Advanced Materials & Processes, 1996, 150(5): 39-41.
[3] DUBOV A A. A study of metal properties using the method of magnetic memory [J]. Metal Science and Heat Treatment, 1997, 39(9/10): 401-405.
[4] WILSON J W, TIAN G Y, BARRANS S. Residual magnetic field sensing for stress measurement [J]. Sensors and Actuators A, 2007, 135(2): 381-387.
[5] DONG Li-hong, XU Bin-shi, DONG Shi-yun, CHEN Qun-zhi, WANG Dan. Variation of stress-induced magnetic signals during tensile testing of ferromagnetic steels [J]. NDT & E International, 2008, 41(3): 184-189.
[6] YANG En, LI Lu-ming, CHEN Xing. Magnetic field aberration induced by cycle stress [J]. Journal of Magnetism and Magnetic Materials, 2007, 312(1): 72-77.
[7] DONG Li-hong, XU Bin-shi, DONG Shi-yun, CHEN Qun-zhi, WANG Yu-ya, ZHANG Lei, WANG Dan, YIN Da-wei. Metal magnetic memory testing for early damage assessment in ferromagnetic materials [J]. Journal of Central South University of Technology, 2005, 12(S2): 102-106.
[8] DONG Li-hong, XU Bin-shi, DONG Shi-yun, YE Ming-hui, CHEN Qun-zhi, WANG Dan, YIN Da-wei. Metal magnetic memory signals from surface of low-carbon steel and low-carbon alloyed steel [J]. Journal of Central South University of Technology, 2007, 14(1): 24-27.
[9] LENG Jian-cheng, XU Min-qiang, XU Ming-xiu, ZHANG Jia-zhong. Magnetic field variation induced by cyclic bending stress [J]. NDT & E International, 2009, 42(5): 410-414.
[10] DUBOV A A. The method of metal magnetic memory—The new trend in engineering diagnostics [J]. Welding in the World, 2005, 49(S): 314-319.
[11] SHAO Xiao-wei, ZHANG Jun. Study on wavelet analysis in metal magnetic memory forecasts the fault of borehole casing well [C]// Proceedings of the 6th World Congress on Intelligent Control and Automation. Piscataway: Institute of Electrical and Electronics Engineers Inc, 2006: 5557-5561. (in Chinese)
[12] ZHANG Jun, WANG Biao, JI Bing-yu. Signal processing for metal magnetic memory testing of borehole casing based on wavelet transform [J]. Acta Petrolei Sinica, 2006, 27(2): 137-140. (in Chinese)
[13] ZHANG Jun, WANG Biao. Recognition of signals for stress concentration zone in metal magnetic memory tests [J]. Proceedings of the CSEE, 2008, 28(8): 144-148. (in Chinese)
[14] MAO Yi-mei, QUE Pei-wen. Application of Hilbert-Huang signal processing to ultrasonic non-destructive testing of oil pipelines [J]. Journal of Zhejiang University: Science A, 2005, 7(2): 130-134.
[15] HUANG N E, SHEN Z, LONG S R, WU M C, SHIH H H, ZHENG Q, YEN N C, TUNG C C, LIU H H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceedings of the Royal Society of London A, 1998, 454: 903-995.
[16] PENG Z K, PETER W T, CHU F L. An improved Hilbert-Huang transform and its application in vibration signal analysis [J]. Journal of Sound and Vibration, 2005, 286(1/2): 187-205.
Foundation item: Project(10772061) supported by the National Natural Science Foundation of China; Project(A200907) supported by the Natural Science Foundation of Heilongjiang Province, China; Project(20092322120001) supported by the PhD Programs Foundations of Ministry of Education of China
Received date: 2009-06-15; Accepted date: 2009-09-19
Corresponding author: LENG Jian-cheng, Doctoral candidate; Tel: +86-451-86418020; E-mail: lbyljc@163.com
(Edited by YANG You-ping)
