氯化稀土溶液射流热解反应器流体动力学的数值模拟
来源期刊:中国有色金属学报(英文版)2015年第3期
论文作者:吕 超 赵秋月 张子木 豆志河 张廷安 赵洪亮
文章页码:997 - 1003
关键词:数值模拟;氯化稀土;射流;热解反应器
Key words:numerical simulation; rare earth chloride; jet-flow; pyrolysis reactor
摘 要:基于直接热解氯化稀土溶液制备稀土氧化物技术,设计一种新型射流热解反应器,并采用CFD方法对反应器内压力、速度等流体动力学特性进行了数值模拟。结果表明:射流热解反应器喉管处自主产生的动压(p)与燃气的进口速度(v)呈二次函数关系(p=0.06v2+0.23v-4.49)。欲使氯化稀土溶液热解反应充分利用燃料燃烧所产生的热量,需在进料口施加一定的压力,此压力与燃料的进口速度呈二次函数关系(p=v2+3v-4.27)。进料口的直径增加到原来的1.25和1.5倍,稀土氧化物的吸入量分别增加了30%和60%以上。整个反应器内流体流动主要受燃料的入口速度影响,且在喉管附近速度形成波峰,随物料加入速度急剧下降,到射流反应器末端速度趋于平缓。
Abstract: Rare earth oxide was prepared via direct pyrolysis of rare earth chloride solution. Based on this technique, a new-type jet-flow pyrolysis reactor was designed, and then the fluid dynamics (pressure and velocity) inside the reactor was numerically simulated using a computational fluid dynamics method. The self-produced pressure (p) and the fuel inlet velocity (v) satisfied a quadratic function, p=0.06v2+0.23v-4.49. To fully utilize the combustion-generated heat in pyrolysis of rare earth chloride, an appropriate external pressure p=v2+3v-4.27 should be imposed at the feed inlet. The 1.25- and 1.5-fold increase of feed inlet diameter resulted in decline of adsorption dynamic pressure, but the intake of rare earth chloride increased by more than 30% and 60%, respectively. The fluid flow in the reactor was affected by the feeding rate; the fluid flow peaked near the throat of venturi and gradually smoothed down at the jet-flow reactor’s terminal along with the sharp decline of feeding rate.
Trans. Nonferrous Met. Soc. China 25(2015) 997-1003
Chao  1,2, Qiu-yue ZHAO, Zi-mu ZHANG1, Zhi-he DOU1, Ting-an ZHANG1, Hong-liang ZHAO1
1,2, Qiu-yue ZHAO, Zi-mu ZHANG1, Zhi-he DOU1, Ting-an ZHANG1, Hong-liang ZHAO1
1. Key Laboratory of Ecological Utilization of Multi-metal Intergrown Ores, Ministry of Education, School of Materials and Metallurgy, Northeastern University, Shenyang 100819, China;
2. Northeast Petroleum University at Qinhuangdao, Qinhuandao 066004, China
Received 29 April 2014; accepted 18 August 2014
Abstract: Rare earth oxide was prepared via direct pyrolysis of rare earth chloride solution. Based on this technique, a new-type jet-flow pyrolysis reactor was designed, and then the fluid dynamics (pressure and velocity) inside the reactor was numerically simulated using a computational fluid dynamics method. The self-produced pressure (p) and the fuel inlet velocity (v) satisfied a quadratic function, p=0.06v2+0.23v-4.49. To fully utilize the combustion-generated heat in pyrolysis of rare earth chloride, an appropriate external pressure p=v2+3v-4.27 should be imposed at the feed inlet. The 1.25- and 1.5-fold increase of feed inlet diameter resulted in decline of adsorption dynamic pressure, but the intake of rare earth chloride increased by more than 30% and 60%, respectively. The fluid flow in the reactor was affected by the feeding rate; the fluid flow peaked near the throat of venturi and gradually smoothed down at the jet-flow reactor’s terminal along with the sharp decline of feeding rate.
Key words: numerical simulation; rare earth chloride; jet-flow; pyrolysis reactor
1 Introduction
Rare earth oxides are widely used in magnetic materials, catalytic materials, hydrogen storage materials, optical glass, optical fiber, and luminescent materials. Rare earth oxides are traditionally produced via oxalic acid-based or ammonium bicarbonate-based precipitation of rare earth chlorides, followed by roasting of rare earth precipitate. However, the precipitation and roasting steps in this procedure will generate abundant wastewater and gas. This procedure is also encountered with disadvantages of low production efficiency, large loss of raw materials, and severe environmental risks. Therefore, our team proposed a new approach for preparation of rare earth oxides: direct pyrolysis of rare earth chloride solutions. We developed a core installation for jet-flow pyrolysis with independent intellectual property rights. This jet-flow pyrolysis reactor was featured with high reaction speed, short reaction time, reaction uniformity, high product quality, complete gas-phase absorption, and no gas-phase escape. Based on the low-temperature pyrolysis of rare earth chloride solutions, the low-cost green preparation of rare earth oxides was achieved.
The design and research on pyrolysis reactors are the keys for realization of pyrolysis, and there are many researches in this field [1]. The experience in preparation of rare earth luminescent materials via spray pyrolysis has been used [2-6]. So far, Venturi tubes have never been used in the rare earth chloride solution. Based on the Venturi tubes and original jet-flow reactor, a new type of Venturi jet-flow reactor was established to prepare rare earth chlorides.

Fig. 1 Flow chart of pyrolysis process
Combined with pyrolysis technique [7] and Venturi jet-flow reactor technique, a new-type jet-flow pyrolysis reactor was designed. Thereby, the rare earth chlorides were directly pyrolyzed into rare earth oxides using the gas-generated heat, thus achieving high efficiency, economic and environmental effects. The technical process of jet-flow pyrolysis is shown in Fig. 1. In the technical process, the gas combustion and expansion at the left inlet of the jet-flow pyrolysis reactor will form a high-speed air flow, and the gas flow passing the throat of Venturi tube will be accelerated. Under the action of the applied pressure, the rare earth chloride solution enters the reactor via the liquid supplying pool and is atomized at high temperature. The vaporized gas will be mixed and heat-exchanged with the combustion- produced gas, thus transforming the rare earth chlorides into rare earth oxides. The gas-solid phases will be separated in the cyclone separator, and the high- temperature end-gas and the pyrolyzed gas will be absorbed by the alkali liquid in the lye absorption pool. Based on the research of Venturi tubes [8-10], the jet-flow pyrolysis reactor was numerically simulated and the changes of pressure field and velocity field inside the reactor were investigated.
2 Reactor geometry
The reactor consists of three parts, including combustion (fuel gas inlet), jet pyrolyzation and outlet. The structure of jet pyrolyzation reactor is shown in Fig. 2 and its dimensions are as follows:
Length of reactor, LR=0.85 m; Diameter of fuel gas inlet, Din,fg=0.01 m; Length of Venturi tube, LV=0.1 m; Diameter of Venturi tube, DV =0.025 m; Diameter of LaCl3 inlet in the middle of the Venturi tube, Din,LaCl3=0.01 m; Diameter of the main pipe, D=0.05 m; Length of main pipe, L1=0.15 m and L2=0.3 m; Length of reducer pipe, Lr1=Lr2=0.14 m.
3 Mathematical model
3.1 Governing equations
Standard k-ε turbulence model [11] is used to simulate the pressure and velocity fields in the jet pyrolyzation reactor. The governing equations are as follows:
Continuity equation:
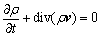 (1)
(1)
Momentum equation:
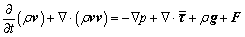 (2)
(2)
where ρ is fluid density, p is fluid pressure, μ is fluid viscosity, t is time, v is velocity vector, F is the body force exerted on unit fluid mass, and 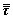 is the phase stress-strain tensor contributed by viscosity and Reynolds stress:
is the phase stress-strain tensor contributed by viscosity and Reynolds stress:
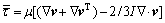 (3)
(3)
Species equation:
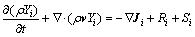 (4)
(4)
where Ji is the diffusion flux of species i, which arises due to concentration gradients, Ri is the net production rate of the reaction, Yi is local mass fraction of each species, and Si is the rate of creation by addition from the dispersed phase plus any user-defined source.
Energy equation [12,13]:

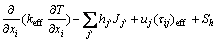 (5)
(5)
where
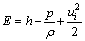 (6)
(6)
and
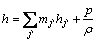 (7)
(7)
where 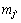 is the mass fraction of species j′ whose enthalpy is defined as
is the mass fraction of species j′ whose enthalpy is defined as
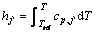 (8)
(8)
The species transmission model of mixture- template [14] is adopted in the combustion model, and eddy-dissipation [15,16] model is used to calculate the chemical reaction rate.

Fig. 2 Dimensions of jet-flow pyrolysis reactor
The net production rate of species i due to reaction r, Ri,r is calculated by smaller one of the two expressions below:
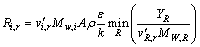 (9)
(9)
 (10)
(10)
where Yp is the mass fraction of any product species p; YR is the mass fraction of a particular reactant R; A is an empirical constant equal to 4.0; B is an empirical constant equal to 0.5.
3.2 Numerical methods and boundary conditions
In this work, we simulated the chemical reaction inside the jet-flow pyrolysis reactor with CH4 and O2 combustion reactions separately and lanthanum chloride as a continuous phase. The whole jet-flow pyrolysis reactor was selected as the computing area, and the walls were supposed to be adiabatic.
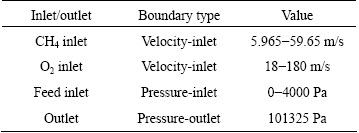
Pressure and velocity are coupled by SIMPLE algorithm, and second-upwind differencing scheme is used for governing equations. The computations are considered converged when the residuals for all quantities are less than 10-3, except for energy equation with the residual below 10-6. The boundary conditions are listed in Table 1.
Table 1 Boundary conditions
3.3 Mesh model
Figure 3 shows the mesh model of the jet pyrolyzation reactor. The three-dimensional hexahedral meshes are used to model parts 1 and 2, and part 2 of venture is locally refined by tetrahedral. Moreover, a preliminary mesh-independent study was carried out.
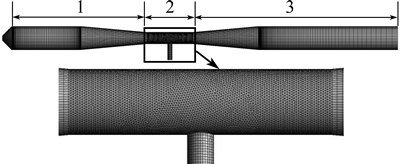
Fig. 3 Schematic grid of jet pyrolyzation reactor
4 Results and discussion
4.1 Mesh-independence verification
Three grid sizes of 90, 230 and 440 k were considered to simulate complex flows during the pyrolyzation. Figures 4(a) and (b) show the axial distributions of pressure and velocity, respectively, with three different grid numbers. The results show very small differences (<5%) between the grids of 230 k and 440 k, but not between 230 k or 440 k and 90 k. Based on the above results, all the subsequent simulations were performed with 230 k computational cells.
4.2 Experimental verification
Figure 5 shows the comparison between the physical experiment results and the simulation results on LaCl3 mass flow rate. The deviations between the physical experiment results and the simulation results were less than 10% and acceptable, which proved that the setting of boundary conditions was accurate and the selected model was correct.
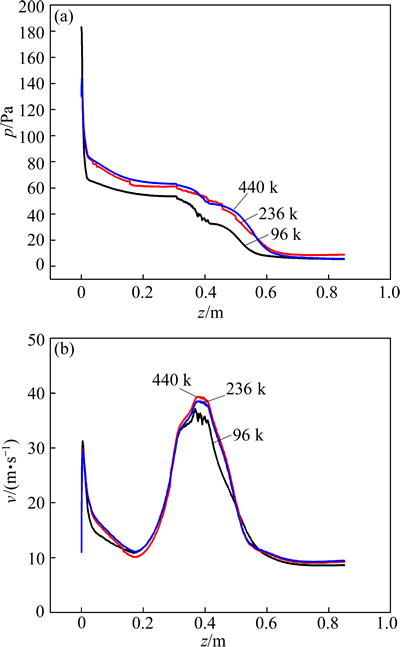
Fig. 4 Mesh-independence verification of pressure (a) and velocity (b)
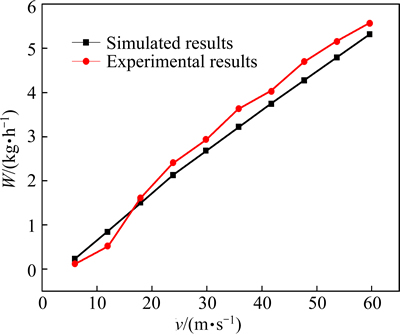
Fig. 5 Comparison between simulated LaCl3 mass flow results and experimental results
We selected the theoretical calculation results of typical intra-reactor reaction products and compared them with the numerical simulation results. The major final product was La2O3. During the chemical reactions inside the jet pyrolysis reactor, the simulated results and calculated results were well consistent for the second-stage product (La2O3), with error less than 10%, (Fig. 6), indicating that the numerical simulation was accurate.
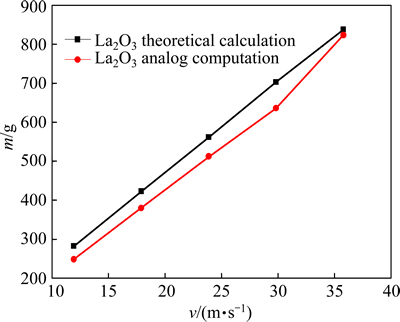
Fig. 6 Comparison between simulated results and calculated results on La2O3 with different gas velocities
4.3 Pressure field
Along with the increasing inlet velocity (v), the dynamic pressure (p) was rising at the jet-flow pyrolysis reactor’s throat (Fig. 7), and the two parameters satisfied a quadratic function: p=0.06v2+0.23v-4.49. Along with the increasing inlet velocity, more heat was produced from combustion. For full utilization of heat, an external pressure was exerted on the feed inlet, which ensured that the feed amount per unit time, the feed rate at the inlet, and the applied external pressure satisfied a quadratic function: p=v2+3v-4.27.
Figure 8 shows that feeding amount is affected by the inlet rate of CH4 and the external pressure. When the pressure is less than 400 Pa, feeding amount increases with the increasing of the inlet rate of CH4. When the pressure is more than 400 Pa, feeding amount is affected mainly by the pressure.

Fig. 7 Self-produced and external pressures with different fuel inlet velocities
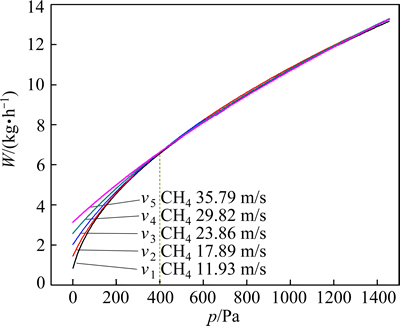
Fig. 8 Feeding amount of LaCl3 with different external pressures
The density of the rare earth chloride solution changed with its concentration. The external pressure should be different so as to fully utilize the combustion-produced heat. The density was larger at a higher concentration, and thus the solution could not enter the reactor easily and required a larger external pressure (Fig. 9).
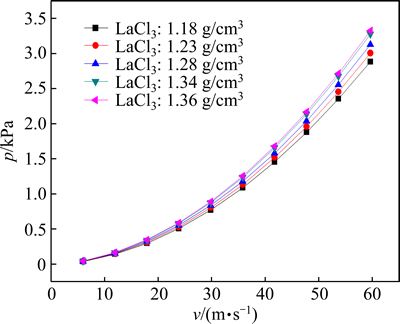
Fig. 9 Self-produced pressure with different concentrations of LaCl3
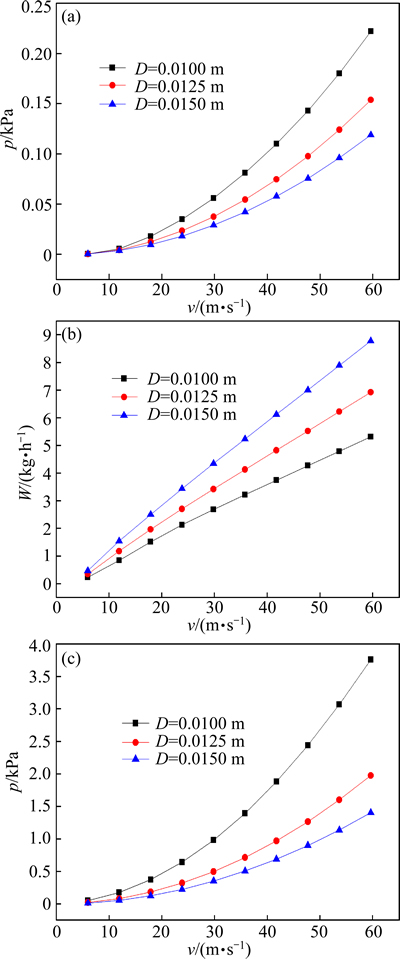
Fig. 10 Influence of different diameters of LaCl3 inlet on self-produced pressure (a), feeding amount of LaCl3 (b) and external pressure (c)
Figure 10(a) shows the changes of spontaneous adsorption dynamic pressure generated by the jet-flow pyrolysis reactor after the feed inlet diameter was changed. Clearly, after the inlet diameter increased from 0.01 to 0.0125 (1.25-fold) or to 0.015 m (1.5-fold), the adsorption dynamic pressure decreased and satisfied a quadratic function with the inlet rate. Figure 10(b) shows the relationship between the feeding amount of spontaneous adsorption and the inlet rate after the feed inlet diameter was changed. Clearly, when the inlet diameter was enlarged by 1.25- and 1.5-fold, the feeding amount and the inlet rate satisfied a linear function. Figure 10(c) shows the relationship between the required external pressure and the inlet rate under the aim of fully utilizing the combustion-produced heat. Clearly, the required external pressure decreased along with the increasing feed inlet diameter. The curve between the external pressure and the inlet rate was basically consistent with the curve between the adsorption dynamic pressure and the inlet rate. After the feed inlet diameter was enlarged by 1.25- or 1.5-fold, the spontaneous dynamic pressure at the throat of Venturi tube decreased, but the intake of rare earth chloride solution increased by more than 30% or 60%. The variation of feed inlet diameter affected the feeding amount more severely than the spontaneous dynamic pressure, and thus with a larger feed inlet diameter, the required external pressure was smaller under the same conditions.
4.4 Velocity field
Then, three straight lines inside the reactor were selected for analysis on-line speed variation. The three lines were X-axis (y=0), the parallel line 0.01 m above X-axis (y=0.01), and the parallel line 0.01 m below X-axis (y=-0.01) (Fig. 11).

Fig. 11 Monitoring line in axial position
The velocity at initial position in the reactor was 0, because the gas nozzle was near y=0, and the initial seeds at upper and low ends were both 0 (Fig. 12(a)). As the gas entered the straight pipeline via the nozzle, the rate was generated on the line and started to rise at z=0.17 m, because the combustion-produced high-temperature exhaust gas started to enter the diameter-variant channel. At z=0.31 m, the rate peaked, because the high- temperature exhaust gas went through the diameter- variant channel to the throat of Venturi tube, but at the center of the throat, the materials entered the inlet vertically, which partially offset the horizontal speed. The zone between z=0.41 m and z=0.55 m was rate-dead, because of the interaction between the vertical entrance of materials and the horizontal speed of gas. The speed was recovered and gradually increased after z=0.55 m.
The gas inlet speed was large at the initial stage, but starting from the straight pipes, the space expansion rate decreased and the pipeline was straight since z=0.17 m, the speed gradually increased (Fig. 12(b)). The speed was maximized at z=0.385 m, because of the interaction between the inlet feeding rate and the combustion- produced high-temperature exhaust gas and the increasing speed (Fig. 12(b)). The speed decreased and stabilized in the diameter-variant channel.
Figure 12(c) shows that the speed was zero at the initial position, but the rate decreased starting from the straight pipes, and the speed gradually increased since z=0.17 m, which were basically consistent with Fig. 12(a). The rate fluctuated slightly at z=0.36 m because of the feeding materials, and the speed was maximized at z=0.385 m because of the interaction between the inlet feeding rate and the combustion-produced exhaust gas. The speed decreased starting from the diameter-variant channel until the straight pipeline.

Fig. 12 Velocity distributions at different monitoring lines
As shown in Fig. 13, the fluid flow in the reactor was affected by the feeding rate of fuel, and the rate peaked near the throat of Venturi tube, and gradually smoothened down at the jet-flow reactor’s terminal along with the sharp decline of feeding rate. Based on the rate changing trend near the throat of Venturi tube, the heat transfer and mass transfer during pyrolysis can be strengthened via the diffusion of fluid components and the homogenization of temperature. The smoothing rate at the outlet would prevent the backward flow at the connection between the outlet and the cyclone separator, and facilitate the diffusion of high-temperature smoke and the pyrogenated gases. It would also prolong the retention time of lanthanum oxide particles, facilitate gas-solid separation, promote the normal process of reaction, and prevent the products from accumulation in the reactor.
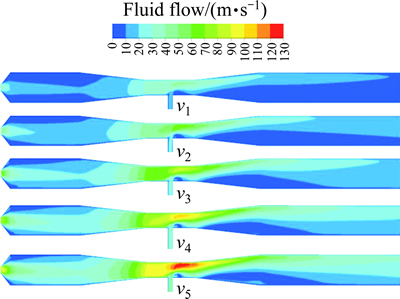
Fig. 13 Contour of velocity
5 Conclusions
1) The self-produced pressure and the fuel inlet velocity satisfied a quadratic function p=0.06v2+ 0.23v-4.49. To fully utilize the combustion-generated heat during pyrolysis of rare earth chloride, a certain amount of pressure p=v2+3v-4.27 should be imposed at the feed inlet, so as to maintain the feeding rate per unit time.
2) Self-produced pressure decreased with the increasing diameter of feed inlet, while more than 30% LaCl3 solution could be inhaled, and the needed external pressure decreased.
3) The fluid flow in the jet-flow pyrolysis reactor is mainly affected by fuel inlet velocity, which peaked near the throat of Venturi tube and gradually smoothened down at the jet-flow reactor’s terminal along with the sharp decline of feeding rate.
References
[1] YANG Z G, LIU X P, YANG Z D, ZHUANG G Q. BAI Z H, ZHANG H X, GUO Y F. Preparation and formation mechanism of levoglucosan from starch using a tubular furnace pyrolysis reactor [J]. Journal of Analytical and Applied Pyrolysis, 2013, 102: 83-88.
[2] QI Fa-xin. Research on rare earth doped yttrium aluminum garnet phosphor synthesized by spray pyrolysis [D]. Nanjing: Nanjing University of Technology, 2006: 1-27. (in Chinese)
[3] SOUMAHORO I, SCHMERBER G, DOUAYAR A, COLIS S, ABD-LEFDIL M, HASSANAIN N, BERRADA A, MULLER D, SLAOUI A, RINNERT H, DINIA A. Structural, optical, and electrical properties of Yb-doped ZnO thin films prepared by spray pyrolysis method [J]. Journal of Applied Physics, 2011, 109(3): 1-5.
[4] ZHOU Y H, LIN J. Luminescent properties of YVO4: Dy3+ phosphors prepared by spray pyrolysis [J]. Journal of Alloys and Compounds, 2006: 856-859.
[5] LING Xiao-qiao. Studies on preparation of nano-oxysulfide via pyrolysis of rare earth complexes with sulphur-contaning ligands [D]. Dalian: Dalian Maritime University, 2009: 9-11. (in Chinese)
[6] FENG Zhi-li. Study on decomposition kinetics, simulation and experiment in multi-grade circulation and fluidzing for siderite ore [D]. Wuhan: Huazhong University of Science and Technology, 2011: 7-15. (in Chinese)
[7] GRIECO E, BALDI G. Analysis and modelling of wood pyrolysis [J]. Chemical Engineering Science, 2011, 66(4): 650-660.
[8] WANG H J. The work principle and structure of Venturi tube in nozzle inner [J]. Journal of Southwest University of Science and Technology, 2004, 19(2): 41-44.
[9] WANG Z Y, ZHANG X D, YANG H Z. Numerical simulation of cavitation flow field in the venture [J]. Computers and Applied Chemistry, 2006, 23(10): 939-942.
[10] XIE F, WU Z S. Numerical simulation and experimental study of gas-solid two-phase flow in venturi tubes [J]. Journal of Power Engineering, 2007, 27(2): 237-241.
[11] WANG Fu-jun. The analysis of computational fluid dynamics: principle and application of CFD software [M]. Beijing: Tsinghua University Press, 2004. (in Chinese)
[12] VAKIL A, GREEN S I. Stagnation pressure, the Bernoulli equation, and the steady-flow energy equation [J]. International Journal of Mechanical Engineering Education, 2011, 39(2): 130-138.
[13] YANG Xia-wei, ZHU Jing-chuan, HE Dong, LAI Zhong-hong, NONG Zhi-sheng, LIU Yong. Optimum design of flow distribution in quenching tank for heat treatment of A357 aluminum alloy large complicated thin-wall workpieces by CFD simulation and ANN approach [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(5): 1442-1451.
[14] LILLEBERG B,·ERTESVAG I S, KNEER D C R, CHRIST D, RIAN K E. Numerical simulation with an extinction database for use with the eddy dissipation concept for turbulent combustion [J]. Flow Turbulence Combust, 2013, 91: 319-346.
[15] KASSEM H I, SAQR K M, ALY H S, SIES M M, WAHID M A. Implementation of the eddy dissipation model of turbulent non-premixed combustion in open foam [J]. International Communications in Heat and Mass Transfer, 2011, 38(3): 363-367.
[16] HU G, WANG H G, QIAN F. Numerical simulation on flow, combustion and heat transfer of ethylene cracking furnaces [J]. Chemical Engineering Science, 2011, 66(8): 1600-1611.
吕 超1,2,赵秋月1,张子木1,豆志河1,张廷安1,赵洪亮1
1. 东北大学 材料与冶金学院,多金属共生矿生态化利用教育部重点实验室,沈阳 110819;
2. 东北石油大学 秦皇岛分校,秦皇岛 066004
摘 要:基于直接热解氯化稀土溶液制备稀土氧化物技术,设计一种新型射流热解反应器,并采用CFD方法对反应器内压力、速度等流体动力学特性进行了数值模拟。结果表明:射流热解反应器喉管处自主产生的动压(p)与燃气的进口速度(v)呈二次函数关系(p=0.06v2+0.23v-4.49)。欲使氯化稀土溶液热解反应充分利用燃料燃烧所产生的热量,需在进料口施加一定的压力,此压力与燃料的进口速度呈二次函数关系(p=v2+3v-4.27)。进料口的直径增加到原来的1.25和1.5倍,稀土氧化物的吸入量分别增加了30%和60%以上。整个反应器内流体流动主要受燃料的入口速度影响,且在喉管附近速度形成波峰,随物料加入速度急剧下降,到射流反应器末端速度趋于平缓。
关键词:数值模拟;氯化稀土;射流;热解反应器
(Edited by Yun-bin HE)
Foundation item: Projects (51204040, U1202274) supported by the National Natural Science Foundation of China; Projects (2010AA03A405, 2102AA062303) supported by the National High-tech Research and Development Program of China; Project (2012BAE01B02) supported by the National Science and Technology Support Program of China; Project (N130702001) supported by the Fundamental Research Funds for the Central Universities, China
Corresponding author: Ting-an ZHANG; Tel: +86-24-83687715; E-mail: zta2000@163.net
DOI: 10.1016/S1003-6326(15)63690-1

