耦合初始微结构的不连续动态再结晶模型
来源期刊:中国有色金属学报(英文版)2018年第11期
论文作者:钟茜婷 黄林科 王磊 刘峰 董晓明 张忠铧
文章页码:2294 - 2306
关键词:不连续动态再结晶;动力学模型;晶界;初始显微组织
Key words:discontinuous dynamic recrystallization (DDRX); kinetic model; grain boundary; initial microstructure
摘 要:为了定量描述和预测中低层错能金属热加工过程中不连续动态再结晶(DDRX)的动力学过程,通过考虑原始晶粒尺寸分布特征、初始晶界(GBs)的曲率效应和GBs的连续消耗作用,构建新的基于物象的动力学模型。采用Incoloy 028合金进行压缩试验以获得动力学数据(再结晶晶粒的尺寸和体积分数)和显微组织。结果表明,DDRX过程特征参数,即流变应力、再结晶分数和晶粒尺寸演变的模型计算结果与实验匹配良好;在此基础上,提出再结晶晶粒长大的热动力学关系,即:动力学能垒随热力学驱动力的增大而不断减小。
Abstract: In order to describe and predict the kinetic process of discontinuous dynamic recrystallization (DDRX) during hot working for metals with low to medium stacking fault energies quantitatively, a new physically-based model was proposed by considering the characteristics of grain size distribution, capillary effect of initial grain boundaries (GBs) and continuous consumption of GBs. Using Incoloy 028 alloy as a model system, experiments aiming to provide kinetic data (e.g., the size and volume fraction of recrystallized grain) and the associated microstructure were performed. Good agreement is obtained between model predictions and experimental results, regarding flow stress, recrystallized fraction and grain size evolution. On this basis, a thermo-kinetic relationship upon the growth of recrystallized grain was elucidated, i.e., with increasing thermodynamic driving force, the activation energy barrier decreases.
Trans. Nonferrous Met. Soc. China 28(2018) 2294-2306
Xi-ting ZHONG1, Lin-ke HUANG1, Lei WANG1, Feng LIU1, Xiao-ming DONG2, Zhong-hua ZHANG2
1. State Key Laboratory of Solidification Processing, Northwestern Polytechnical University, Xi’an 710072, China;
2. Baoshan Iron & Steel Co. Ltd. Research Institute (R&D Center), Shanghai 201900, China
Received 7 August 2017; accepted 28 March 2018
Abstract: In order to describe and predict the kinetic process of discontinuous dynamic recrystallization (DDRX) during hot working for metals with low to medium stacking fault energies quantitatively, a new physically-based model was proposed by considering the characteristics of grain size distribution, capillary effect of initial grain boundaries (GBs) and continuous consumption of GBs. Using Incoloy 028 alloy as a model system, experiments aiming to provide kinetic data (e.g., the size and volume fraction of recrystallized grain) and the associated microstructure were performed. Good agreement is obtained between model predictions and experimental results, regarding flow stress, recrystallized fraction and grain size evolution. On this basis, a thermo-kinetic relationship upon the growth of recrystallized grain was elucidated, i.e., with increasing thermodynamic driving force, the activation energy barrier decreases.
Key words: discontinuous dynamic recrystallization (DDRX); kinetic model; grain boundary; initial microstructure
1 Introduction
During hot deformation, discontinuous dynamic recrystallization (DDRX) taking place by nucleation and growth in materials with low to medium stacking fault energies (SFEs), plays a crucial role in grain refinement and hence has been a subject of fundamental research and industrial application for decades [1-6]. To control and improve the microstructure and the corresponding mechanical properties of products arising from DDRX, it is necessary to model the kinetics, in terms of flow stress curve, recrystallized fraction and grain size, which together characterize the DDRX process. Generally, the developed kinetic models can be divided into two types: phenomenological and physical models. Note that these models focused here do not involve the discrete methods, such as cellular automata [7,8], Monte Carlo [9,10], phase field [11,12] and level set [13,14] models.
Generally, phenomenological models [1-4,15-18], further, consist of the constitutive, analytical and empirical models, where, the Zener-Hollomon parameter Z is often adopted to describe the flow stress and the steady-state recrystallized grain size, and the kinetics of DDRX is obtained by JMAK approach [19-22]. These phenomenological models are widely used in industrial applications [2,3,15,16]. However, such model involves considerable fitting parameters and meanwhile, does not consider the physically based nucleation law and grain boundary (GB) migration driven by energy difference. These non-physical parameters and only deriving the static conditions point out the need of physically based quantitative model.
Regarding the physically based model, extensive endeavors [5,23-28] are made mainly considering the following transformation processes, including work- hardening, dynamic recovery, nucleation and GB migration [5,23]. Work hardening and dynamic recovery determine the dislocation density, whose evolution is generally described using constitutive models [29-31]. On this basis, the driving force of DDRX can be quantitatively evaluated. In the view of the typical nucleation theory, dynamic substructure nucleation (i.e., climb of edge dislocation [25] and evolution of subgrain [23,32,33]) is proposed. The GB migration is driven by the energy difference on both sides, which is affected by the dislocation density [23-28], the capillary effect [24,25] and the solute/precipitate effect [25,27]. Following the framework of classical JMAK equation [19-22] and the Cahn model [34], the capability of describing kinetic process is proven.
Despite the success in describing DDRX kinetics, the current physically based models [5,23-28] pay little attention on the original microstructure characteristics (i.e., grain size, grain size distribution, and differently kinetic properties of GBs), which are centers to the evolution of DDRX. As far as the authors know, only the effects of grain size on the evolution of dislocation density [24] and the nucleation at GBs [23,26-28], as two typical examples exhibit the effect of initial microstructure characteristics on DDRX, have been usually investigated. However, we argue that, additionally, at least three characteristics of microstructures are still missing in the modeling, which are briefly summarized as follows.
(1) Grain size distribution. Previous models [26-28] are mostly based on a mean-field approximation (i.e., a grain is considered to be representative of the whole microstructure); while, experimentally [1,35], the grain sizes always follow a distribution, which, in turn, influences the evolution of dislocation density and hence the DDRX kinetics [23,25].
(2) The capillary effect of initial GB on the new recrystallized grain nucleated at GBs. Experiments suggest that [36-38], the newly recrystallized grain will be influenced by the capillary effect of the GB, which, however, is often overlooked [23,25,26] or modeled in a phenomenological way without a clear physical implication [27,28].
(3) GBs are consumed in a continuous way. In the commonly adopted phase transformation theory (i.e., Cahn model [34]), saturated GB consumption is assumed, which obviously is inconsistent with the experimental and computational results showing that GBs are consumed in a gradual and continuous way [1,2,6,24,35-39], since GBs in the system possess different kinetic properties from one to each other [40].
So, one may conclude that, a comprehensively, kinetic model of DDRX incorporating the characteristics of initial microstructure, is still not available. Considering the effect of grain size on the evolution of dislocation density, we further devote to modeling the kinetics with respect to the microstructure characteristics, including grain size distribution, capillary effect of initial GB using the thermodynamic extreme principle (TEP) [41,42], and continuous consumption of GB using the modified Cahn model. On this basis, DDRX experiments are performed for Incoloy 028 alloy [43-46]. Then, a correlation between thermodynamic driving force and kinetic barrier involved in the DDRX is discussed.
2 Model derivations
2.1 Physical structure of DDRX
To explore the kinetics of DDRX, the true stress–true strain curve is widely utilized, as schematically shown in Fig. 1(a), where three typical stages are presented [1,29]. At the beginning of deformation (i.e., Stage I), recovery takes place but without the occurrence of DDRX; compared with softening due to the recovery, work-hardening due to the deformation plays a dominated role, which accounts for an increased stress with strain. Once the critical condition (ec, sc) is reached, the microstructure evolution is mainly controlled by the concomitant recrystallization and deformation. Thus, a competition between the work-hardening and the softening due to recrystallization prevails, and correspondingly, the stress firstly increases and then decreases, thereby exhibiting a peak (Stage II) in Fig. 1(a). Once a balance is arrived between the recrystallization and the deformation, a steady-state (i.e., Stage III) is reached.
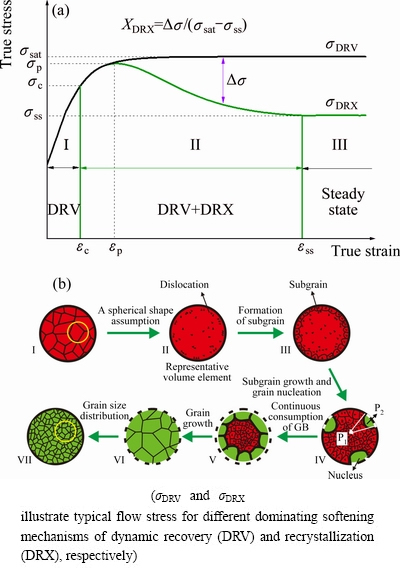
Fig. 1 Schematic sketch showing true stress-true strain curves (a) and physical structure of DDRX (b)
For a system with a given grain size distribution, a grain is selected as the representative volume element (RVE) (see Fig. 1(b)-I). With progressing hot deformation, the dislocation density is substantially increased (Fig. 1(b)-II), thus resulting in the formation and growth of sub-grains (Fig. 1(b)-III). Once the size of subgrains nearby the GB reaches the critical size of recrystallized nuclei [23,32,33], the DDRX will take place: the recrystallized nuclei form at GBs and propagate into the nearby grain interior (Fig. 1(b)-IV). Most importantly, the newly recrystallized grain will be influenced due to the capillary effect of the initial GB (see P1 and P2 in Fig. 1(b)-IV) and the GBs are progressively consumed (Fig. 1(b)-IV and V). Ultimately, the RVE (Fig. 1(b)-VI) and then the system (Fig. 1(b)-VII), are totally covered by the recrystallized grains.
2.2 Kinetic model of DDRX
2.2.1 Dislocation density evolution
The dislocation density providing the driving force of DDRX, is determined by combination of work hardening and dynamic recovery [29-31]. KOCKS and MECKING [29,30] developed an effective approach to describe the relationship between dislocation density ρ and plastic strain ε:
 (1)
(1)
where b is the absolute value of burgers vector, R is the grain size, and K1 and K2 are the material constants associated with the dislocation storage and annihilation process, dependent on the deformation condition. As such, the instantaneous dislocation density as a function of the strain during deformation can be determined.
2.2.2 Nucleation at GBs by subgrain growth
As described in Section 2.1, the dislocation motion leads to the subgrain formation, whose averaged growth rate is expressed as [23,26]
 (2)
(2)
where  is the average subgrain size, γsub is the sub-boundary energy, Kc (=10) is the material parameter [47,48], and Msub(=M0,subexp(-Qsub/(RgT))) is the subgrain boundary mobility with M0,sub as the pre-exponential factor and Qsub as the activation energy. Conventionally, Qsub is assumed to be constant [23,26]. From the recent studies [49,50], however, it is increasingly believed that, a decreasing apparent activation energy prevails, accompanied by an increasing driving force. Further, a correlation between thermodynamic driving force and activation energy is suggested as [49] Qsub=Q0-AsubPsub with Q0 as the activation energy at the start of subgrain growth, Psub(=2γsub/
is the average subgrain size, γsub is the sub-boundary energy, Kc (=10) is the material parameter [47,48], and Msub(=M0,subexp(-Qsub/(RgT))) is the subgrain boundary mobility with M0,sub as the pre-exponential factor and Qsub as the activation energy. Conventionally, Qsub is assumed to be constant [23,26]. From the recent studies [49,50], however, it is increasingly believed that, a decreasing apparent activation energy prevails, accompanied by an increasing driving force. Further, a correlation between thermodynamic driving force and activation energy is suggested as [49] Qsub=Q0-AsubPsub with Q0 as the activation energy at the start of subgrain growth, Psub(=2γsub/ ) as the driving force of subgrain growth, and Asub as the constant value representing the extent of the above correlation. This correlation is adopted in modeling and, further, will be confirmed later.
) as the driving force of subgrain growth, and Asub as the constant value representing the extent of the above correlation. This correlation is adopted in modeling and, further, will be confirmed later.
Subsequently, the subgrain growth leads to the initial GB nucleation, and generally, a well-accepted nucleation criterion is expressed as [1]
 (3)
(3)
where γgb is the GB energy, and τ(=αμb2) is the dislocation energy per unit length with α (=0.5 [1,48]) as a constant and μ as the shear modulus.
In the RVE (Fig. 1(b)), the subgrain radius r in the vicinity of the initial GB can be approximated by a Rayleigh distribution [1,23,32,33,42], and thus, the fraction of subgrain, whose size is greater than the instantaneous critical nucleation size rc can be further determined as

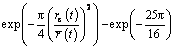
Therefore, the effective number of nuclei for a spherical assumption is given as N(t)=Nsub(t)F(t)=  , with Nsub as the total number of subgrains nearby the GB and R0 as the radius of the initial grain. Ultimately, the nucleation rate in a RVE becomes
, with Nsub as the total number of subgrains nearby the GB and R0 as the radius of the initial grain. Ultimately, the nucleation rate in a RVE becomes
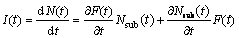 (4)
(4)
2.2.3 Growth of recrystallized grain
By incorporating the capillary effect of initial GBs (Fig. 1(b)-IV; Section 2.1) and using the concept of thermodynamic extreme principle (TEP), the migration velocity of recrystallized GB of grain i in the RVE can be expressed as (see details in Appendix A)
 (5)
(5)
where Mgb(=M0,gbexp(-Qgb/(RgT))) is the mobility of recrystallized GB, with M0,gb as the pre-exponential factor and Qgb as the activation energy. Analogous to Section 2.2.2, an increasing Qgb prevails as the recrystallization proceeds, and thus, Qgb=Q0-AgbPgb. For the RVE, the average growth rate is given by a volume average of all the recrystallized grains:
 (6)
(6)
Correspondingly, the average dislocation density, ρDRX, is defined by a surface-area-weighted average over all the grains [51]:
 (7)
(7)
2.2.4 Fraction of recrystallization in one deformed grain
Following Cahn model, the volume of new phase per unit GB area, is expressed as


where I is the nucleation rate per unit GB area (i.e., Eq. (4)), and vDRX is the growth velocity of the new phase (i.e., Eq. (6)). The extended volume is obtained as (see details in Appendix B)
 (8)
(8)
where (dS/dt)(=S0exp(-Kst)) is the instantaneous consumption rate of GB, with Ks as the kinetic coefficient for GB consumption and S0=3/R0 as the area of initial GB per volume.
Ultimately, the fraction of recrystallization is obtained for an initially deformed grain with volume  :
:
 (9)
(9)
The average grain size of dynamically recrystallized grain in one deformed grain is express by the initial grain size and recrystallized fraction:
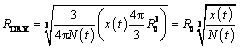 (10)
(10)
2.2.5 Prediction of overall fraction, average grain size and flow stress
With the fraction of DDRX in one deformed grain and the Rayleigh distribution of all the original grain sizes f(R0), the DDRX fraction in the entire system can be expressed as
 (11)
(11)
Furthermore, the average grain size in the whole recrystallized region is expressed as
 (12)
(12)
where the average grain sizes in deformed and recrystallized region are described as
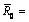

and

respectively.
Following the rule of mixture [26], the flow stress is
 (13)
(13)
where the stresses in deformed and recrystallized regions are described as

and

respectively.
Up to now, a DDRX kinetic framework has been proposed, considering the characteristics of the grain size distribution, the capillary effect of initial GBs and the continuous consumption of GBs. Note that, these characteristics, related closely to the initial microstructure, will be confirmed by the current experiments, as described in Section 5.1.
2.3 Recipe of DDRX model
A procedure for applying the present model is summarized and illustrated in Fig. 2, which is described concisely as follows.
(1) Dislocation density evolution. Generally, using double-differentiation method proposed by JONAS et al [52,53], true stress–true strain curves (σDRX–ε; Fig. 1(a)) with DDRX as the raw data, are firstly transformed into true stress–true strain curves (σDRV–ε; Fig. 1(a)) without DDRX, which are then fitted by Eq. (1). As a result, the evolution of dislocation density is obtained.
(2) Nucleation. Based on the dislocation density evolution, the nucleation criterion and the evolution of average subgrain size can be determined using Eqs. (2) and (3), respectively. In combination with the average subgrain size and the Rayleigh distribution, the evolution of subgrain size in the RVE can be estimated. As such, the nucleation kinetics could be determined according to the nucleation criterion.
(3) Growth. The evolution of dislocation density in deformed and recrystallized grain, together with the capillary effect of initial GBs, enables the description of recrystallized grain growth.

Fig. 2 Flowchart for procedure of applying present DDRX model
(4) Recrystallization. Combination of Steps 1-3 permits a well-described recrystallization in one deformed grain, i.e. REV. Then, by considering the Rayleigh distribution, the DDRX kinetics of the whole system will be determined.
3 Experimental
Incoloy corrosion-resistant 028 alloy with chemical composition Ni-27%Cr-29%Fe-0.03%C-3.5%Mo- 2.5%Mn-1.0%Cu (mass fraction) was studied here. Before testing, all the specimens were solution-treated at 1473 K for 2 h followed by water quenching. Compression specimens with the diameter of 8 mm and the length of 12 mm were prepared according to ASTM: E209-00 (2010) standard. Constant-strain rate compression tests were carried out on a Gleeble 3500 testing system. Microstructural observation of original and deformed specimens on sections parallel to the compression axis was performed via optical microscopy (OM) and scanning electron microscope (SEM) equipped with an electron backscattered diffraction (EBSD) analyzer. Grain sizes were measured by the mean linear intercept method.
4 Results
4.1 Flow stress, DDRX kinetics and microstructures
Figures 3(a) and (b) show a series of true stress- true strain (i.e., s-e) curves for Incoloy 028 alloy under different deformation conditions. Obviously, all the flow curves display distinct peak points, followed by softening and steady-state condition, attesting to the typical characteristics of the DDRX flow curve. Besides, the overall levels of the flow stress curves increase with decreasing the deformation temperature (Fig. 3(a)), as well as with increasing the strain rate (Fig. 3(b)); this has been interpreted elsewhere [1-6]. Applying the double- differentiation method proposed by JONAS et al (see Fig. 1(a)) [52,53], the DDRX kinetic curves are obtained and shown in Figs. 3(c) and (d). A detailed kinetic analysis for DDRX of 028 alloy can be seen in Ref. [45].

Fig. 3 True stress-true strain curves (a, b) and DDRX kinetics (c, d) under different deformation conditions
Subjected to the above deformations, the steady-state microstructures are obtained and shown in Fig. 4, where, as compared with initial coarse equiaxed grains with a large quantity of twin boundaries (Fig. 4(a)), the deformed specimens exhibit finely equiaxed grains (Figs. 4(b)-(f)), further attesting to the occurrence of DDRX. Correspondingly, the average grain sizes are shown in Fig. 5, where, the decrease of temperature, as well as the increase of strain rate, prefers to refine the resulting microstructure. Furthermore, the typical microstructure evolution at one selected deformation condition (i.e., 1423 K and 0.01 s-1), is demonstrated in Fig. 6 [46]. At e=0.15 corresponding to the peak stress on the flow curve (Fig. 3(b)), the nucleation of new fine grains occurs at the original GBs (Fig. 6(a)). With increasing strain, DDRX proceeds, reflected by the increased number of recrystallized grains and nucleus growth (e =0.35, Fig. 6(b)). When the strain is further reached to 0.6 (Fig. 6(c)), the area of interest is almost covered by recrystallized grains, which, however, are non-uniform. Ultimately, the originally deformed grains are totally replaced by uniformly recrystallized grains (e=0.9, Fig. 6(d)). Accordingly, the averaged grain size is shown in Fig. 5(b). Moreover, the associated size distribution of recrystallized grains can be discerned and displayed in Fig. 7, where, with the increase of strain, the average recrystallized grain size firstly increases from 10 to 21 μm, followed by a saturated value of 22 μm.
4.2 Model application
Corresponding to different combinations of deformation temperature (T) and stain rate ( ), a fixed Raleigh distribution (f(R0)) is assumed for the initial grain size at the start of the calculation (Fig. 8(b)). Fits of the current model to the experimental results (Fig. 3) are performed, as summarized in Fig. 2. The essential physical parameters applied in the current model are given in Table 1. As indicated in Fig. 3, the true stress–true strain curves and the kinetics of DDRX, at different temperatures and strain rates, are described well. Moreover, the average size at steady-states (Dss) under different deformation conditions, as well as the evolution of averaged recrystallized size at one selected deformation condition (i.e. 1423 K and 0.01 s-1), is predicted and shown in Fig. 5, where the corresponding experimental data are also shown for comparison. Good agreements have been achieved between model predictions and experimental measurements. One can see that, the current model is successfully applied to describing the experimental results for 028 alloy, including the true stress–true strain curves, the recrystallization kinetics and the average grain size.
), a fixed Raleigh distribution (f(R0)) is assumed for the initial grain size at the start of the calculation (Fig. 8(b)). Fits of the current model to the experimental results (Fig. 3) are performed, as summarized in Fig. 2. The essential physical parameters applied in the current model are given in Table 1. As indicated in Fig. 3, the true stress–true strain curves and the kinetics of DDRX, at different temperatures and strain rates, are described well. Moreover, the average size at steady-states (Dss) under different deformation conditions, as well as the evolution of averaged recrystallized size at one selected deformation condition (i.e. 1423 K and 0.01 s-1), is predicted and shown in Fig. 5, where the corresponding experimental data are also shown for comparison. Good agreements have been achieved between model predictions and experimental measurements. One can see that, the current model is successfully applied to describing the experimental results for 028 alloy, including the true stress–true strain curves, the recrystallization kinetics and the average grain size.

Fig. 4 Microstructures of samples at different states
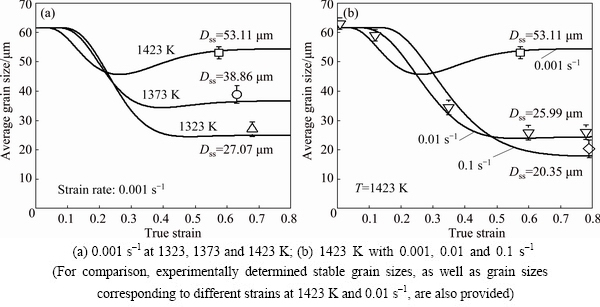
Fig. 5 Predictions of evolution of average grain size under different deformation conditions

Fig. 6 EBSD images of microstructures deformed to different strains at 1423 K and 0.01 s-1 (with permission of Ref. [45])
5 Discussion
As described in Section 2, the characteristics of the original microstructure are considered in the modeling, as reflected by three assumptions. Here, it is aimed to, first, provide experimental evidences for the assumptions, then, demonstrate some information that cannot be obtained experimentally, and finally, suggest a correlation between thermodynamic driving force and kinetic energy barrier for the growth of recrystallized grain, as well as its possible application in designing DDRX.
5.1 Experimental evidence for model assumption
Based on the current experiment results, the rationality of the three assumptions adopted for the current modeling will be proven as follows.
(1) Grain size distribution. Non-uniform grains are clearly indicated in the initial microstructure (see Fig. 4(a)). For a sophisticated characterization, EBSD is therefore carried out and the corresponding result is illustrated in Fig. 8. It is observed that, the initial grains with an average size of 63 μm are randomly- orientated and equiaxed (Fig. 8(a)). The measured and simulated grain size distributions applying Rayleigh distribution which has been widely utilized in the previous studies [1,23,32,33,42], are described in Fig. 8(b).

Fig. 7 Size distributions of recrystallized grain at different true strains, 1423 K and 0.01 s-1
Fig. 8 Characteristics of initial microstructure
(2) Capillary effect of initial GBs. Following the theory of recrystallization [1-5], nucleation occurs by the bulging of initial GBs (as marked in Fig. 6(a)). This bulged GB segment will be influenced by the adjacent GB segment (not involved in nucleation and successive growth) since they are closely bound to each other. This interactive effect between the two kinds of GB segments will, in return, make the above adjacent GB bulged. On this basis, the bulging of GB segment nearby the newly formed nuclei (as depicted in Fig. 6(b)), is a strong evidence of capillary effect of initial GBs.
(3) Continuous consumption of GBs. As shown in Fig. 6(c), GBs with different misorientation angles are involved. It is believed that the kinetic properties of GBs can vary by orders of magnitude from one GB to the other, depending on the GB types [28], and hence, GBs in the initial microstructure continuously take part in the DDRX. This augment can be supported by Fig. 6(a), where, only some GB segments are covered by new nucleus, in contrast with the saturated assumption of GB where the initial GBs are totally covered by nuclei. Actually, the progressive consumption of GBs has also been observed both experimentally [1,2,35–38] and computationally [6,24,39].
Table 1 Definitions and values of parameters used in model (Typically at 1423 K, 0.01 s–1)
5.2 Analysis of intermediate state
By using the data in Table 1, the present model could predict the size distribution of recrystallized grain at any intermediate state. This is superior to previous models without considering the grain size distribution [26-28] where only mean grain size is predicted. For a selected deformation condition (1423 K and 0.01 s-1), Fig. 7 shows the grain size distribution of recrystallized grains with increasing the strain, where, the average grain first increases from 8 to 24 μm (Figs. 7(a)-(c)) and then saturates at a stable size of 24 μm (Fig. 7(d)). Accordingly, the experimentally measured average grain size and grain size distributions are shown in Figs. 5 and 7 as well. Model predictions match well with experimental results with minor discrepancies, which are probably induced by the prior assumption of Rayleigh distribution of subgrain. By applying the present models and the true stress–true strain curves as the initially raw data, the microstructures (e.g., average grain size and grain size distribution) could be estimated. Correspondingly, the current model permits to select optimized deformation conditions, to achieve desired grain sizes.
5.3 Correlation between thermodynamic driving force and kinetic energy barrier
In this modeling, particularly in dealing with the GB migration (Eq. (5)), a correlation between thermo- dynamic driving force and kinetic energy barrier is assumed. This correlation has been qualitatively proven in a lot of experiments [1-5], e.g., the activation energy increases with the decrease of driving force. Therefore, for the convenience of modeling, an empirical relation is approximately assumed here. Surprisingly, this correlation does exist for the steady-state subjected to different deformation conditions. The corresponding driving forces and activation energies (Qss) are determined and shown in Fig. 9, where, a linear relationship prevails, i.e., the activation energy decreases with increasing the driving force. Hence, one may conclude that, the correlation not only prevails in the process of DDRX under a given deformation condition, but also presents for the steady stages after various deformation conditions. On this basis, a correlation between the stable grain size and the driving force is determined as well (see Fig. 9), which reveals that, for steady-states, the increase of thermodynamic driving force tends to reduce the stable grain size. Generally, for a certain temperature or a certain strain rate, increasing the strain rate or decreasing the deformation temperature tends to increase the thermodynamic diving force. This follows that, a condition with high strain rate and low temperature is preferable to obtain refined grain size after DDRX. This conclusion is well consistent with the predictions by the parameter  with Qdef as the deformation activation energy, which is conventionally and widely used in describing the relationship between the stable grain size and the deformation condition. Obviously, the consistency between conclusions made from thermodynamic/kinetic correlation and the parameter Z, proves the rationality of the correlation between the thermodynamic driving force and kinetic energy barrier.
with Qdef as the deformation activation energy, which is conventionally and widely used in describing the relationship between the stable grain size and the deformation condition. Obviously, the consistency between conclusions made from thermodynamic/kinetic correlation and the parameter Z, proves the rationality of the correlation between the thermodynamic driving force and kinetic energy barrier.
As addressed previously, to predict the stable grain size, the initial deformation conditions (e.g., strain rate  and temperature T) are necessarily involved in the parameter Z. Whereas, in this study, the correlation between thermodynamic driving force and kinetic energy barrier corresponding to deformation conditions are demonstrated. This gives us an inspiration: if a relationship among deformation conditions, thermo- dynamic/kinetic correlation and microstructures (e.g., grain size) could be determined, the stable grain size, as well as the evolved size, might be predicted more effectively, arising from a quantitative linkage between the initial or final condition and the kinetic process.
and temperature T) are necessarily involved in the parameter Z. Whereas, in this study, the correlation between thermodynamic driving force and kinetic energy barrier corresponding to deformation conditions are demonstrated. This gives us an inspiration: if a relationship among deformation conditions, thermo- dynamic/kinetic correlation and microstructures (e.g., grain size) could be determined, the stable grain size, as well as the evolved size, might be predicted more effectively, arising from a quantitative linkage between the initial or final condition and the kinetic process.

Fig. 9 Relationship between driving force and activation energy/average grain size for steady-states
6 Conclusions
1) A new physically-based model, by considering the characteristics of grain size distribution, capillary effect of initial grain boundaries (GBs) and continuous consumption of GBs, is proposed.
2) Regarding the true stress–true strain curve, recrystallized fraction, average grain size and recrystallized grain size distribution, the model predictions match well with the experimental observations.
3) The steady-state recrystallization grain size decreases with the increase of the thermodynamic driving force, which is consistent with the discipline under the deformation condition with high strain rate and low temperature.
4) A linear correlation between the thermodynamic driving force and kinetic energy barrier is uncovered: with increasing thermodynamic driving force, the activation energy barrier decreases.
Appendix A: Growth of recrystallized grain derived using thermodynamic extreme principle (TEP)
The total Gibbs energy of the system stems G deriving from two parts, i.e., the store energy GD and GB energy Gγ. The store energy due to plastic deformation is in the form of dislocation:
 (A1)
(A1)
where ρi is the dislocation density of the newly recrystallized grain i, which can be estimated by Eq. (1) and taking into account the formation of nuclei at different times tc,i,
 (A2)
(A2)
The GB energy consists of the initially deformed and recrystallized grain area, but excluding the cross-sectional area due to the GB nucleation:
 (A3)
(A3)
Then, the total Gibbs energy change of the system is given by

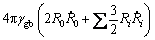 (A4)
(A4)
Upon growth, only the recrystallized GBs migrate with a velocity v expressed by time derivative of the recrystallized grain radius  , under the thermodynamic driving force P, and thus, the dissipation Q is given by Pv. By assuming the relation v=MP, the dissipation becomes a quadratic function of v as
, under the thermodynamic driving force P, and thus, the dissipation Q is given by Pv. By assuming the relation v=MP, the dissipation becomes a quadratic function of v as 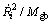 , and finally, total dissipation in system becomes [41,42]
, and finally, total dissipation in system becomes [41,42]
 (A5)
(A5)
where Mgb is the high angle GB mobility.
The conservation law of system volume gives
 →
→ (A6)
(A6)
which is constrained by
 (A7)
(A7)
According to TEP, the evolution path of the system corresponds to the maximum of the total dissipation in the system. Thus, the maximum of Q can be obtained using the Lagrange multiplier method:
 (A8)
(A8)
Substituting Eqs. (A4)–(A7) into Eq. (A8) gives the Lagrange multipliers β, ω and  as β=-2, ω=2τρ+ 4γ/R0 and
as β=-2, ω=2τρ+ 4γ/R0 and  .
.
Appendix B: Modified Cahn model
Considering the characteristic of continuous transition for GBs, we assume that at any time, the GBs in the system (initial area S0) can be divided into two parts: the covered GBs, Scov(t), and uncovered GBs, S(t). Thus, the conservation law of GB area gives
S0=Scov(t)+S(t) (B1)
The instantaneous consumption rate of GB is proportional to the instantaneously uncovered GBs in the system with a kinetic coefficient Ks (i.e., represents the nucleation ability of GB), and thus,
 (B2)
(B2)
Substituting Eq. (B1) into Eq. (B2) and integrating give the uncovered GBs as a function of time:
S(t)=S0exp(-Kst) (B3)
Thus, the GB consumption rate becomes
 (B4)
(B4)
Hence, the extended volume is expressed as
 (B5)
(B5)
where VGB can be evaluated by Cahn model [34].
References
[1] HUMPHREYS F J, HATHERLY M. Recrystallization and related annealing phenomena [M]. 2nd ed. Oxford: Elsevier, 2004.
[2] SAKAI T, BELYAKOV A, KAIBYSHEV R, MIURA H, JONAS J J. Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions [J]. Progress in Materials Science, 2014, 60: 130-207.
[3] SAKAI T, JONAS J J. Dynamic recrystallization: Mechanical and microstructural considerations [J]. Acta Metallurgica, 1984, 32: 189-209.
[4] DOHERTY R D, HUGHES D A, HUMPHREYS F J, JONAS J J, JENSEN D JUUL, KASSNER M E, KING W E, McNELLEY T R, McQUEEN H J, ROLLETT A D. Current issues in recrystallization: A review [J]. Materials Science and Engineering A, 1997, 238: 219-274.
[5] HUANG K, LOGE R E. A review of dynamic recrystallization phenomena in metallic materials [J]. Mater Design, 2016, 111: 548-574.
[6] ROLLETT A D. Overview of modeling and simulation of recrystallization [J]. Progress in Materials Science, 1997, 42: 79-99.
[7] LIU Xiao, LI Luo-xing, HE Feng-yi, ZHOU Jia, ZHU Bi-wu, ZHANG Li-qiang. Simulation on dynamic recrystallization behavior of AZ31 magnesium alloy using cellular automaton method coupling Laasraoui-Jonas model [J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 2692-2699.
[8] HALLBERG H, WALLIN M, RISTINMAA M. Simulation of discontinuous dynamic recrystallization in pure Cu using a probabilistic cellular automaton [J]. Computational Materials Science, 2010, 49: 25-34.
[9] ROLLETT A D, LUTON M J, SROLOVITZ D J. Microstructural simulation of dynamic recrystallization [J]. Acta Metallurgica et Materialia, 1992, 40: 43-55.
[10] PECZAK P. A Monte Carlo study of influence of deformation temperature on dynamic recrystallization [J]. Acta Metallurgica et Materialia, 1995, 43: 1279-1291.
[11] TAKAKI T, HISAKUNI Y, HIROUCHI T, YAMANAKA A, TOMITA Y. Multi-phase-field model to simulate microstructure evolutions during dynamic recrystallization [J]. Materials Transactions, 2008, 49: 2559-2565.
[12] TAKAKI T, HISAKUNI Y, HIROUCHI T, YAMANAKA A, TOMITA Y. Multi-phase-field simulations for dynamic recrystallization [J]. Computational Materials Science, 2009, 45: 881-888.
[13] BOULAIS-SINOU R, SCHOLTES B,  D PINO, MOUSSA C, POITRAULT I, BOBIN I, MONTOUCHET A, BERNACKI M. Full field modeling of dynamic recrystallization in a global level set framework, application to 304L stainless steel [C]// The 12th International Conference on Numerial Methods in Industrial Forming Processes. Troyes, France, 2016, 02005: 1-6.
D PINO, MOUSSA C, POITRAULT I, BOBIN I, MONTOUCHET A, BERNACKI M. Full field modeling of dynamic recrystallization in a global level set framework, application to 304L stainless steel [C]// The 12th International Conference on Numerial Methods in Industrial Forming Processes. Troyes, France, 2016, 02005: 1-6.
[14] HALLBERG H. A modified level set approach to 2D modeling of dynamic recrystallization [J]. Modelling and Simulation in Materials Science and Engineering, 2013, 21(8): 085012.
[15] DERBY B. The dependence of grain size on stress during dynamic recrystallization [J]. Acta Metallurgica et Materialia, 1991, 39: 955-962.
[16] OHASHI M, ENDO T, SAKAI T. Effect of initial grain size on the dynamic recrystallization of nickel [J]. Journal of the Japan Institute of Metals, 1990, 54: 435-441.
[17] McQUEEN H J, RYAN N D. Constitutive analysis in hot working [J]. Materials Science and Engineering A, 2002, 322: 43-63.
[18] LI Yu-fei, WANG Zhen-hong, ZHANG Lin-ying, LUO Chao, LAI Xin-chun. Arrhenius-type constitutive model and dynamic recrystallization behavior of V-5Cr-5Ti alloy during hot compression [J]. Transactions of Nonferrous Metals Society of China, 2015, 25: 1889-1900.
[19] KOLMOGOROV A. On the statistical theory of the crystallization of metals [J]. Bull Acad Sci USSR Ser Math, 1937, 1: 355-359.
[20] JOHNSON W, MEHL R. Reaction kinetics in processes of nucleation and growth [J]. Transactions of the Metallurgical Society of AIME, 1939, 135: 416-458.
[21] AVRAMI M. Kinetics of phase change: I. General theory [J]. Journal of Chemical Physics, 1939, 7: 1103-1112.
[22] AVRAMI M. Kinetics of phase change: II. Transformation time relations for random distribution of nuclei [J]. Journal of Chemical Physics, 1940, 8: 212-224.
[23] CRAM D G, ZUROB H S, BRECHET Y J M, HUTCHINSON C R. Modelling discontinuous dynamic recrystallization using a physically based model for nucleation [J]. Acta Materialia, 2009, 57: 5218-5228.
[24] DING R, GUO Z X. Coupled quantitative simulation of microstructural evolution and plastic flow during dynamic recrystallization [J]. Acta Materialia, 2001, 49: 3163-3175.
[25] SOMMITSCH C, MITTER W. On modelling of dynamic recrystallization of FCC materials with low stacking fault energy [J]. Acta Materialia, 2006, 54: 357-375.
[26] MOMENI A, EBRAHIMI G R, JAHAZI M, BOCHER P. Microstructure evolution at the onset of discontinuous dynamic recrystallization: A physics-based model of subgrain critical size [J]. Journal of Alloys and Compounds, 2014, 587: 199-210.
[27] BERNARD P, BAG S, HUANG K, LOGE R E. A two-site mean field model of discontinuous dynamic recrystallization [J]. Materials Science and Engineering A, 2011, 528: 7357-7367.
[28] BELTRAN O, HUANG K, LOGE R E. A mean field model of dynamic and post-dynamic recrystallization predicting kinetics, grain size and flow stress [J]. Computational Materials Science, 2015, 102: 293-303.
[29] KOCKS U F, MECKING H. Physics and phenomenology of strain hardening: The FCC case [J]. Progress in Materials Science, 2003, 48: 171-273.
[30] MECKING H, KOCKS U F. Kinetics of flow and strain-hardening [J]. Acta Metallurgica, 1981, 29: 1865-1875.
[31] LIN Yong-cheng, CHEN Xiao-min. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working [J]. Materials and Design, 2011 32: 1733-1759.
[32] HOLM E A, MIODOWNIK M A, ROLLETT A D. On abnormal subgrain growth and the origin of recrystallization nuclei [J]. Acta Materialia, 2003, 51: 2701-2716.
[33] ZUROB H S, BRECHET Y, DUNLOP J. Quantitative criterion for recrystallization nucleation in single-phase alloys: Prediction of critical strains and incubation times [J]. Acta Materialia, 2006, 54: 3983-3990.
[34] CAHN J W. The kinetics of grain boundary nucleated reactions [J]. Acta Metallurgica, 1956, 4: 449-459.
[35] FROMMERTA M, GOTTSTEINB G. Mechanical behavior and microstructure evolution during steady-state dynamic recrystallization in the austenitic steel 800H [J]. Materials Science and Engineering A, 2009, 506: 101-110.
[36] WUSATOWSKA-SARNEK A M, MIURA H, SAKAI T. Nucleation and microtexture development [J]. Materials Science and Engineering A, 2002, 323: 177-186.
[37] SHI Zhao-xia, YAN Xiao-feng, DUAN Chun-hua, ZHAO Ming-han. Effect of strain rate on hot deformation characteristics of GH690 superalloy [J]. Transactions of Nonferrous Metals Society of China, 2017, 27: 538-550.
[38] MIURA H, SAKAI T, MOGAWA R, GOTTSTEIN G. Nucleation of dynamic recrystallization at grain boundaries in copper bicrystals [J]. Scripta Materialia, 2004, 51: 671-675.
[39] RIOS P R, GLICKSMAN M E. Topological and metrical analysis of normal grain growth in three dimensions [J]. Acta Materialia, 2007, 55: 1565-1571.
[40] ALEXANDER K C, SCHUH C A. Exploring grain boundary energy landscapes with the activation-relaxation technique [J]. Scripta Materialia, 2013, 68: 937-940.
[41] FISCHER F D, SVOBODA J, PETRYK H. Thermodynamic extremal principles for irreversible processes in materials science [J]. Acta Materialia, 2014, 67: 1-20.
[42] SVOBODA J, FISCHER F D. A new approach to modelling of non-steady grain growth [J]. Acta Materialia, 2007, 55: 4467-4474.
[43] WANG Lei, LIU Feng, ZUO Qiang, CHEN Chang-feng. Prediction of flow stress for N08028 alloy under hot working conditions [J]. Materials and Design, 2013, 47: 737-745.
[44] WANG Lei, LIU Feng, CHENG Jia-jia, ZUO Qiang, CHEN Chang-feng. Hot deformation characteristics and processing map analysis for nickel-based corrosion resistant alloy [J]. Journal of Alloys and Compounds, 2015, 623: 69-78.
[45] WANG Lei, LIU Feng, CHENG Jia-jia, ZUO Qiang, CHEN Chang-feng. Arrhenius-type constitutive model for high temperature flow stress in a nickel-based corrosion-resistant alloy [J]. Journal of Materials Engineering and Performance, 2016, 25: 1394-1406.
[46] WANG Lei, LIU Feng, ZUO Qiang, CHENG Jia-jia, CHEN Chang-feng. Processing map and mechanism of hot deformation of a corrosion-resistant nickel-based alloy [J]. Journal of Materials Engineering and Performance, 2017, 26: 392-406.
[47] GALINDO-NAVA E I, RIVERA-DI'AZ-DEL-CASTILLO P E J. A thermodynamic theory for dislocation cell formation and misorientation in metals [J]. Acta Materialia, 2012, 60: 4370-4378.
[48] HUANG Ming-xin, RIVERA-DI'AZ-DEL-CASTILLO P E J, BOUAZIZ O, van der ZWAAG S. Modelling the steady–state deformation stress under various deformation conditions using a single irreversible thermodynamics based formulation [J]. Acta Materialia, 2009, 57: 3434-3438.
[49] YU Tian-bo, HANSEN N, HUANG Xiao-xu. Linking recovery and recrystallization through triple junction motion in aluminum cold rolled to a large strain [J]. Acta Materialia, 2013, 61: 6577-6586.
[50] YU Tian-bo, HANSEN N. Coarsening kinetics of fine-scale microstructures in deformed materials [J]. Acta Materialia, 2016, 120: 40-45.
[51] MONTHEILLET F, LURDOS O, DAMAMME G. A grain scale approach for modeling steady-state discontinuous dynamic recrystallization [J]. Acta Materialia, 2009, 57: 1602-1612.
[52] JONAS J J, QUELENNEC X, JIANG L, MARTIN E. The Avrami kinetics of dynamic recrystallization [J]. Acta Materialia, 2009, 57: 2748-2756.
[53] POLIAK E I, JONAS J J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization [J]. Acta Materialia, 1996, 44: 127-136.
钟茜婷1,黄林科1,王 磊1,刘 峰1,董晓明2,张忠铧2
1. 西北工业大学 凝固技术国家重点实验室,西安 710072;
2. 宝山钢铁有限股份公司研究院,上海 201900
摘 要:为了定量描述和预测中低层错能金属热加工过程中不连续动态再结晶(DDRX)的动力学过程,通过考虑原始晶粒尺寸分布特征、初始晶界(GBs)的曲率效应和GBs的连续消耗作用,构建新的基于物象的动力学模型。采用Incoloy 028合金进行压缩试验以获得动力学数据(再结晶晶粒的尺寸和体积分数)和显微组织。结果表明,DDRX过程特征参数,即流变应力、再结晶分数和晶粒尺寸演变的模型计算结果与实验匹配良好;在此基础上,提出再结晶晶粒长大的热动力学关系,即:动力学能垒随热力学驱动力的增大而不断减小。
关键词:不连续动态再结晶;动力学模型;晶界;初始显微组织
(Edited by Bing YANG)
Foundation item: Project (51431008) supported by the National Natural Science Foundation of China; Projects (2017YFB0703001, 2017YFB0305100) supported by the National Key Research and Development Program of China
Corresponding author: Feng LIU; Tel: +86-29-88460374; Fax: +86-29-88491484; E-mail: liufeng@nwpu.edu.cn
DOI: 10.1016/S1003-6326(18)64874-5

