基于神经网络技术的股票频谱分析

李清峰^{1, 2}，彭文峰¹，何静¹

(1. 湖南商学院 计算机与电子工程学院，湖南 长沙，410205；

2. 中南大学 信息科学与工程学院，湖南 长沙，410083)

摘要：根据艾略特波浪理论以及波浪理论中的各参数具有费波纳奇数列关系的特征，分析股票价格波形的特点；运用人工神经网络模型，提出基于波形分解与重构的神经网络预测方法，给出具体的实现过程。研究结果表明：通过波形分解与重构，把原始价格时间序列分解为规律相对简单、不同频率范围内的子波动序列来提高神经网络的预测精度，实现对特征不同的信号选取不同的参数模型进行预测；采用傅里叶反变换拟合出股价波动变化趋势的曲线，以达到预测股价波动变化周期的目的。

关键词：波浪理论；费波纳奇数列；频谱分析；神经网络

中图分类号：F830.9           文献标志码：A         文章编号：1672-7207(2011)03-0726-05

Frequency analysis in stock by neural network

LI Qing-feng^{1, 2}, PENG Wen-feng¹, HE Jing¹

(1. Department of Computer and Electronic Engineering, Hunan Business College, Changsha 410205, China;

2. School of Information Science and Engineering, Central South University, Changsha 410083, China)

Abstract: According to Elliott wave theory and wave theory of the Fibonacci array, the stock price profile characteristics were analyzed. The neural network was researched and a neural network prediction method was brought out. Its concrete realization process based on wavelet decomposition and reconstruction were made. The results show that through this method, the price function is decomposed into a series of wavelets in different frequency ranges, whose fluctuation rule can be easily grasped. This method increases the neural network prediction precision, and makes it possible to predict signals with prediction models of different parameters. The inverse Fourier transform can be used to fit the stock price fluctuation change tendency, and to forecast stock price fluctuation cycle.

Key words: stock wave theory; Fibonacci array; frequency analysis; artificial neural network

通过对股市价格波动规律的研究有助于揭示金融市场的运行规律，为证券组合的选择、金融资产定价、期货和期权等金融衍生工具定价以及风险管理提供理论基础。然而，股市投资的收益与风险往往是成正比的，即投资收益越高，可能冒的风险越大；因此，对股市预测方法的研究具有极其重要的应用价值和理论意义。随着越来越多的人进入股市进行投资活动，人们迫切需要一种有效的分析方法，能够最大限度地增加收益，降低风险。徐梅^[1]研究基于小波变换的LMSV(Long memory stochastic volatility)模型的估计方法，根据LMSV过程同一尺度和不同尺度下DWT (Discrete wavelet transform)系数的近似不相关性，提出了基于小波变换的LMSV模型参数的伪极大似然估计方法以及潜在波动过程的估计方法。郑宇泉等^[2]在期望均值收益与收益方差模型基础上，采用数据挖掘中聚类的方法，定义一种衡量时间序列样本之间相似程度的指标，这个指标反映了股票间波动行情趋势的异同。夏卿卿^[3]设计了将股票行情时间序列数据转移为多阶均线形态多维度层次结构挖掘模型，分析了形态走势分析中预测目标与输入状态的相关性。吕淑萍^[4]研究了小波分析与神经网络的结合，通过小波分解与重构，把原始价格时间序列分解为规律相对简单、不同频率范围内的子波动序列来提高神经网络的预测精度。这些研究主要是分析股票间波动行情趋势，或对股票价格进行预测，但对股票间波动周期的定量分析不足。在此，本文作者通过对股票波浪图形的时域参数采用神经网络频域系数进行分解，来分析股市价格波动周期，帮助投资者在进行买进卖出决策时提供有益的参考和指导。

1  相关理论

1.1  波浪理论

波浪理论是艾略特^[5]最先提出来的，因此，也被称为艾略特波浪理论。艾略特理论认为，股市价格波动就如同大自然的潮汐一样，一浪跟着一浪，并且周而复始，具有一定的规律性。艾略特波浪理论将股票变动循环周期分为8个浪，其中5个是上升(或是下跌)浪，3个是下跌(或上升)浪。

该理论还认为，每一波浪之间的比例包括波动时间和幅度都接近各自的费波纳奇比率，例如，上升浪的时间周期与下降浪的时间周期、第3浪波动的幅度与第1浪起始点至第1浪最高点之间的距离都符合费波纳奇比率的关系。

1.2  傅里叶级数

傅里叶理论^[6-7]认为1个周期为T的周期信号f(T)可分解成若干正弦信号的叠加，即：

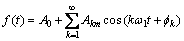
从f(t)的展开式可看到：其分解式中除直流分量外，还包含1，2，3等整数谐波分量，谐波次数越高，其对应的幅值越小。其波形的主要变化趋势由前几项低次谐波确定，高次谐波体现波形的细节变化。

1.3  神经网络技术

神经网络^[15]可以看作是一个多输入单输出的信息处理系统。根据神经元的特性和功能，可以把神经元抽象为一个简单的数学模型，它对信息的处理是非线性的。

神经网络有3个要素：拓扑结构、连接方式和学习规则。随着计算机技术和人工神经网络技术的快速发展，人工神经网络用于股票预测正得到越来越多的关注，尤其是人工神经网络强大的非线性映像能力以及自学习能力，不用像基于时间序列的预测那样主观设定模型，因此，在金融时间序列的预测上具有很大的实用性。

2  波形分析

波浪理论考虑的因素主要有3个：(1) 股价走势所形成的形态；(2) 股价走势图中各个高点和低点所处的相对位置；(3) 完成某个形态所经历的时间。这三者简单地概括为形态、幅度和时间，是波浪理论首先应考虑的，其中，以形态最为重要。

股价的波浪图与正弦函数i(t)=Icos (ωt+φ)曲线相似，见图1。

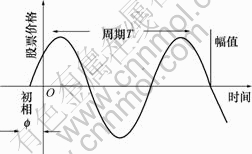
图1  与股票波浪理论对应的正弦波

Fig.1  Sine wave correspondence stock wave theory

正弦函数i(t)与股价的波动一样是起伏变化的，其中也包含3个要素：初相φ、振幅I和角速度ω，如图1所示。其中初相φ代表信号的起始时间，即信号开始变化的时间，它对应股价走势所形成的形态起点(即上升浪抑或下降浪的起始时间)；振幅I对应股价走势图中各个高点和低点所处的相对位置；角速度ω(ω=2π/T)代表信号的周期，其对应股价波动完成某个形态所经历的时间。因此，采用正弦函数来分析股价的波动是比较恰当的，由于股价波动复杂，其对应的正弦函数i(t)的初相φ、振幅I和角速度ω都是变化的函数。

将股票变动循环周期作为正弦函数的1个周期，则股票变动波形中包含了正弦函数的若干次谐波。1次谐波对应股票变动的整个周期，3次谐波对应股票变动的3个下跌(或上升)浪，5次谐波对应股票变动的5个上升(或下跌)浪。按傅里叶级数分解的逆过程(即信号合成)，将正弦函数的1次、3次和5次谐波信号合成便得到与图2所示矩形波图形相似的雏形。当然，由于3次和5次谐波分量随实际股价的波动图变化而不同，因此，得矩形波图形不对称，如图2所示。图2中，t₁≠t₂，即矩形波的占空比σ(σ=t₁/T, T=t₁+t­₂)将发生变化。从图2可以看到：高电平代表股市上升浪，是多头市场；低电平代表股市下跌浪，是空头市场。矩形波的上升沿代表股市的空多逆转信号，矩形波的下降沿代表股市的多空逆转信号。若能计算上升沿和下降沿持续的时间，则能帮助投资者在决策何时买进和卖出时提供有益的参考指导。

图2  与股票涨跌对应的矩形波

Fig.2  Increase and decrease of rectangular wave correspondence stock

3  系统的构造及分析

根据股票时域波形周期前期的重要参数，利用神经网络强大的非线性映射能力，分析时域波形的频谱参数，拟合整个时域波形，以预测周期后期(下降浪或上升浪)的延续时间，即预测下半个周期达到谷底(下降浪)或峰顶(上升浪)的时间。系统整个信号处理过程见图3。

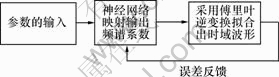
图3  分析系统结构图

Fig.3  Structure block of analytic system

3.1  输入和输出参数的选择

选取股票时域波形周期前期的主要参数时，由于该波形不完整，选前5个上升(或是下跌)浪的特征值，如每个浪的延续时间(t₁~t₅，单位为h)和相对幅值(h₁~h₅，单位为元)，以及变化周期前期每天的威廉指标(S)。其中：

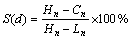
其中：d=1, 2, …, int [(t₁+t₂+t₃+t₄+t₅)/24], int [(t₁+t₂+t₃+ t₄+t₅)/24]表示变化周期前期的总时间(单位为d)；C_n为当天的收盘价；H_n和L_n分别为最近n日内(包括当天)出现的最高价和最低价。

指标S表示的涵义是当天的收盘价在过去的n日中全部价格范围内所处的相对位置。

输出参数对股票波动周期的精度有其特殊要求。用户往往将精度确定到0.05 d，这里将精度定为0.01 d。这样，在频谱分析中，选取1个股票变动循环周期波形的前7次谐波分量。由于波形的形态与谐波的分量系数和频谱系数都有关，为此，将1次谐波系数定为1，后6次谐波的分量系数分别设为a₂，a₃，a₄，a₅，a₆和a₇；频谱系数分别设为b₂，b₃，b₄，b₅，b₆和b₇作为输出参数，因此，可以得到相应的频谱函数X(ω)：

X(ω)=2π[δ(ω-ω₀)+a₂δ(ω-b₂×2ω₀)+a₃δ(ω-b₃×3ω₀)+a₄δ(ω-b₄×4ω₀)+a₅δ(ω-b₅×5ω₀)+a₆δ(ω-b₆×6ω₀)+a₇δ(ω-b₇×7ω₀)]

式中：ω₀=2π/T；T为股票变动循环周期；δ(ω)为频域分析中的单位冲激函数。

3.2  神经网络

由于求解的问题是复杂的非线性问题，系统采用三层(即输入层、隐藏层和输出层)模型结构。其中，隐藏层可以有任意多层，每层单元的输出是下一层的输入。同时，为使系统自主学习并不断提高精度，采用反向传播算法(Back-propagation, BP算法)。该算法过程如下。

输入：层次为m的神经网络，其中第i层结点数为n_i，训练样本集为T。

T={t­₁,…,t₅,h₁,…, h₅,S(d),d=1,2,…,int ((t₁+t₂+t₃+t₄+t₅)/24)}

输出：经过训练的神经网络Y={a₂, …, a₇, b₂, …, b₇, T}

(1) 初始化各层的权系数和偏置。为了加快系统的训练时间，保证系统的收敛性，根据艾略特波浪理论中各次波浪的时间和幅度具有费波纳奇数列和黄金分割的关系特点，初始权系数取0.618或1.618。

(2) 输入训练样本。输入T中的1个样本X=   (X₁, X₂, …, X_n)和期望输出Y=(Y₁, Y₂, …, Y_m)。

(3) 正向传播。从第2层开始到第m层，计算每层单元的输出。令第k层第j个单元的输出记为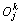。其计算公式如下：

其中：W_ij(t)为t时刻单元与下层单元j间的权系数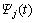；为t时刻单元j的偏值；为t时刻第k-1层单元i的输出。对于输入单元，输出就等于输入，即=。

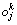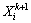(4) 反向传播。输出的误差主要是比较拟合的股票波形与实际波形的吻合程度，这里采用明考斯基距离来确定。由于这里主要考虑波形周期，因此，以明考斯基距离水平误差来表示：

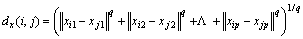
其中：x_ip为实际波形主要点的水平坐标值，如峰值点、谷值点、过均值点等；X_jp为拟合波形对应点的水平坐标值；q根据分析的艾略特波浪层次来取值，层次越多，q取值越小，层次越少，q取值越大(q为正整数)。

若用户同时对股价波动幅度关注，则可将垂直方向的误差引入：

合成误差d(i, j)=[d_x(i,j)+0.618d_y(i, j)]/(1+0.618)。其中：0.618是体现艾略特波浪具有费波纳奇比率关系的特征值。

从输出到第2层，其反馈误差为d(i, j)，然后，从第m层开始直到第2层，计算每层单元的误差。将第k层第j个单元的误差记为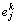，对于输出层单元，误差为：

 (1≤j≤n_m)

对于各隐藏层单元，误差为

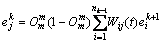 (2≤k≤m-1, 1≤j≤n_k)

 (5) 修正权系数和各单元的偏置为：

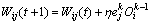
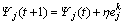
 (6) 根据给定的结束条件判断是否满足。若满足，则算法结束，否则，返回步骤(2)继续执行。这里的结束条件参数可以是d(i, j)，也可以是周期的误差。

3.3  波形的拟合

后6次谐波的分量系数分别设为a₂，a₃，a₄，a₅，a₆和a₇；频谱系数分别为b₂，b₃，b₄，b₅，b₆和b₇，将它们作为输出参数，则可以得到相应的频谱函数X(ω)。

采用傅里叶逆变换：

上述变换公式将频谱函数X(ω)变换成对应的时域表达式X(t)，然后，根据X(t)得出对应的时域波形。从该波形的上升沿和下降沿就可以拾取股票变动中空多逆转信号和多空逆转信号。

4  实验解释及验证

对上面的理论分析进行实验验证。选取上海电力 2009—11—27至2009—12—22共18个工作日的股票行情^[16]，如表1所示；用信息分析与处理软件MATLAB语言工具箱函数来进行运算。以日收盘价绘出其波动图，如图4中实线所示，其中，5个上升浪和3个下跌浪构成1个波动周期。图4中纵坐标表示日收盘价(单位为元)，横坐标表示2009—11—27至2009—12—22共18个工作日。从图4可以看出：从2009—11—27至2009—12—10共10个工作日完成了5个浪的多头市场，故0.618×5ω₀=2π/0.9，得出ω₀= 0.226。。

由a₂=0.534, a₃=0.124, a₄=0.032, a₅=0.012, a₆=a₇= 0, b₂=1.12, b₃=1.21, b₄=1.34, b₅=1.56可得频谱函数：

X(ω)=2π[δ(ω-0.226)+0.534δ(ω-0.578)+0.124δ(ω-0.798)+0.032δ(ω-1.178)+0.012δ(ω-1.578)

其对应的时域函数为：

X(t)=2[sin0.226t+0.534sin0.578t+0.124sin0.798t+0.032sin1.178t+0.012sin1.578t]

表1  上海电力股票行情

Table 1  Data of Shanghai power stock

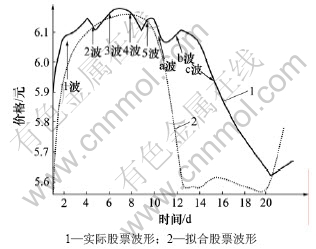
图4  拟合的上海电力股票波形曲线

Fig.4  Composition wave curve of Shanghai power stock

该函数拟合的波形如图4中虚线所示。从图4可见：拟合波形的低电平大约在16.9个工作日结束，其价格与实际由a~c波构成的空头市场在第18个工作日结束的价格误差为6.1%；拟合波形的多空翻转时间为10.1个工作日，其价格与实际由1~5波构成的多头市场在第9.3个工作日结束的价格误差为8.6%。误差主要来源于以下几方面：(1) 在实验过程中只分析了幅频函数X(ω)，没有对相对应的相频函数进行分析；(2) 实线以整数“天”进行描绘，精度不高；(3) 与π的取值精度有关；(4) X(t)函数拟合过程的准确度。

5  结论

(1) 在幅频函数的分析过程中，若能同时分析相频函数的变化关系，则能提高拟合波形的精确度。

(2) 波浪理论一个很明显的不足之处在于投资者较难学习和掌握。从理论上讲，波浪理论的1个完整过程只是1个8浪结构，而且单纯的8浪结构也很简单。但在实际操作中，由于主浪和调整浪都会发生变异，而且存在大浪套小浪、浪中有浪的多层次现象，使得使用波浪理论的投资者在具体确定浪的数量时会发生偏差。波浪层次的确定以及每个浪的起始点的确认是运用频谱分析的两大难点。

(3) 频谱分析只考虑了价格形态上的因素，忽略了交易量和股票基本面的影响。

参考文献：

[1] 徐梅. 金融波动分析的小波和频域方法研究[D]. 天津: 天津大学管理学院, 2003: 102-109.
XU Mei. Study on the wavelet and frequency domain methods of financial volatility analysis[D]. Tianjin: School of Management. Tianjin University, 2003: 102-109.

[2] 郑宇泉, 姜青山, 管河山. 基于聚类的股票波动分析及其应用[J]. 四川大学学报, 2007, 39(S1): 192-195.
ZHENG YU-quan, JIANG Qing-shan, GUAN He-shan. Fluctuation analysis on base of clustering and application[J]. Journal of Sichuan University: Engineering Science Edition, 2007, 39(S1): 192-195.

[3] 夏卿卿. 基于股价均线形态序列的数据挖掘模型[J]. 电子科技大学学报, 2007, 4(6): 459-462.
XIA Qing-qing. Data-mining model based on move-average form series of stock prince[J]. Journal of University of Electronic Science and Technology, 2007, 4(6): 459-462.

[4] 吕淑萍. 小波网络建模预报方法研究及其在股市预测中的应用[D]. 哈尔滨: 哈尔滨工程大学信息学院, 2004: 56-59.
L? Shu-ping. The research on wavelet network prediction model and its application in stock market fForecasting[D]. Harbin: School of Information. Harbin Engineering University, 2004: 56-59.

[5] Daigler R T. Financial futures and option markets: Concepts and strategies[M]. HarperCollins College Publishers, 1994: 283-291.

[6] 何孝星. 证券投资理论与实务[M]. 北京: 清华大学出版社, 2004: 132-135.
HE Xao-xing. Securities investment theory and practice[M]. Beijing: Tsinghua University Press, 2004: 132-135.

[7] 郑君里. 信号与系统[M]. 北京: 人民教育出版社, 1980: 312-316.
ZHENG Jun-li. Signal and system[M]. Beijing: People’s Education Press, 1980: 312-316.

[8] 丁玉美. 数字信号处理[M]. 西安: 西安电子科技大学出版社, 2004: 212-216.
DING Yu-mei. Digital signal proceding[M]. Xi’an: Xi’an University of Electronic Science and Technology, 2004: 212-216.

[9] Shintani M, Linton O B. Is there chaos in the world economy: A nonparametric test using consistent standard errors[J]. International Economic Review, 2008, 44(1): 331-357.

[10] Mandelbrot B B, Taqqu M S. Robust R/S analysis of long-run serial correlation[J]. Bulletin of the International Statistical Institute, 1979, 48(6): 69-99.

[11] Abry P, Veitch D. Wavelet analysis of long rang dependence traffic[J]. IEEE Trans Inform Theory, 1996, 44(1): 2-15.

[12] Kin K L, Lean Y. Mean variance skewness kurtosis based portfolio optimization[C]//Proceeding of the First International Muti-Symposiums on Computational Sciences(IMSCCS’06). Nova Scotia, 2007: 45-59.

[13] Baillie R T. Long memory process and fractional in econometrics[J]. Journal of Econometrics, 2007, 73: 54-59.

[14] Beran J. Estimation of dominating frequency for stationary and nonstationary fractional autoregressive models[J]. Journal of Time Series Analysis, 2009, 21(5): 212-219.

[15] HAN Jia-wei. Data mining: Concepts and techniques[M]. Burnaby: Morgan Kaofmann Publishers Inc, 2006: 89-103.

[16] The stock network platform[EB/OL]. [2009-12-26]. http://www.lh29.com.

(编辑 陈灿华)

收稿日期：2010-06-10；修回日期：2010-08-21

基金项目：国家自然科学基金资助项目(60573057)；湖南省科技计划项目(2010GK3034)

通信作者：李清峰(1965-)，男，湖南邵阳人，副教授，从事数据挖掘、复杂问题的算法研究；电话：13549643089；E-mail: lqf4pwf3@163.com