J. Cent. South Univ. (2012) 19: 453-458

DOI: 10.1007/s11771-012-1024-3

Node deployment strategy optimization for wireless sensor network with mobile base station

LONG Jun(龙军), GUI Wei-hua(桂卫华)

School of Information Science and Engineering, Central South University, Changsha 410083, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: The optimization of network performance in a movement-assisted data gathering scheme was studied by analyzing the energy consumption of wireless sensor network with node uniform distribution. A theoretically analytical method for avoiding energy hole was proposed. It is proved that if the densities of sensor nodes working at the same time are alternate between dormancy and work with non-uniform node distribution. The efficiency of network can increase by several times and the residual energy of network is nearly zero when the network lifetime ends.

Key words: wireless sensor network; mobile base station; network optimization; energy consumption balancing; density ratio of sensor node; network lifetime

1 Introduction

The main function of wireless sensor networks is to gather the information of surrounding environment, manage it and transmit the sensed data to the base station for further processing [1-3]. As the sensor node has limited energy, many researchers focused on how to increase the efficiency of energy use to prolong network lifetime. It is known that the traditional data gathering scheme is based on an assumption that the base station is static. Under such circumstance, the sensor nodes around the base station become the bottlenecks of network performance because of undertaking all loads in the network. Then, the throughput of network declines and these sensor nodes die. So, the network lifetime decreases.

In order to balance the load around the base station, researchers proposed many effective methods. The methods could be devided into the following five categories:

1) Deploy the sensor nodes that have larger initial energy or more sensor nodes in the region which consumes large energy to avoid the energy hole problem. In the researches of energy hole, the distance ratio of sensor node from the base station to the density of sensor node was exclusively discussed in Ref. [3]. LI and MOHAPATRA [4-5] firstly proposed a model applied to analyze the energy hole in wireless sensor network. OLARIU and STOJMENIVIC [6] proved that the energy hole in wireless sensor network is unavoidable under given conditions. The similar researches can be found in Refs. [7-8].

2) Sensor nodes use different transmission power levels to transmit data. As the energy consumption of sensor node is related to transmission distance, the effects caused by energy hole may be relieved if the sensor nodes in different regions employing different transmission distances. For instance, MHATRE and ROSENBERG [10] proposed an alternate transmission mode between single hop and multiple hops. The sensor nodes far away from the base station consume large energy under the circumstance of single hop, while the sensor nodes close to the base station have large energy consumption under the condition of multiple hops. Therefore, employing the alternate mode can balance the energy consumption, and elevate the network lifetime [10]. Similar studies can be found in Ref. [9]. Based on the hierarchical network, the non-uniform clustering algorithm can balance the energy consumptions, which also includes the thinking of employing different transmission power levels [11].

3) Use mobile relays to share the load of sensor nodes around the base station. WANG et al [3] used mobile relays to prolong the lifetime of wireless sensor networks. The research indicated that if the mobile relay moves in the scope of two hops from the base station, the lifetime of network will increase by four times.

4) Employ mobile base station to balance the energy consumption. SHI and LIAO [12] proposed an movement-assisted data gathering scheme. According to the scheme, the base station gathers data while moving along the given buffer area purposefully. It is found that the scheme takes both the energy consumption and load balancing into consideration. Moreover, the scheme supports the data gathering modes both based on the event-driven and inquiry-driven at the same time.

5) Exploit the non-uniform clustering algorithm to avoid the energy hole problem [11]. Different from the classical uniform clustering algorithms such as LEACH algorithm [13] and HEED algorithm [14], most algorithms for avoiding the energy hole employ the idea of non-uniform clustering, for example, LIU et al [11] proposed such kind of algorithm, EADEGG algorithm. Non-uniform clustering algorithm can balance the energy consumption, and prolong the lifetime of the network.

In recent years, wireless sensor technology developed rapidly. The wireless transmission power becomes controllable, that is, the sensor nodes can adjust its transmission power according to its distance from the receiver. For instance, Berkeley mode has 100 transmission power levels [10, 14]. Such sensor nodes can adjust transmission power in accordance with practical application environment in order to reduce the energy consumption of network and prolong network lifetime.

A movement-assisted data gathering scheme was proposed in Ref. [12]. A method was employed to avoid the energy hole problem with non-uniform distribution node of wireless sensor network, and a more accurate formula was given for the ratio of different region to the density of sensor node after strict deduction.

2 Network model and description of problem

2.1 Network models

1) Network structure model

A typical model of wireless sensor network was employed in this work [1-3]. This kind of network is described as a circular area similar to the one shown in Ref. [15]. The difference between our typical network and general network is that the base station is no longer fixed in the centre, while it can move. In addition, the transmission power of sensor node is variable, and the maximal transmission radius is k times of the minimal transmission radius r. Such as the Berkeley mode, it has 100 transmission power levels [10, 14].

2) Energy consumption model

A typical energy consumption model was adopted which specific details can be found in Ref. [14]. The energy consumption of transmitting data can be seen in Eq. (1), while that of receiving data can be found in   Eq. (2).

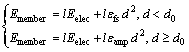                              (1)

                                                               (2)

For a sensor node, the energy consumption of transmitting a bit of data can be seen in Eq. (1) where E_elec represents the energy consumption of transmission circuit. If the transmission distance d is less than the threshold value d₀, the power amplification loss exploits the free space model. If the transmission distance d is greater than or equal to the threshold value d₀, the power amplification loss uses the multi-path attenuation model. Variables ε_fs and ε_amp represent the energy required by power amplification in the two models, respectively. The energy consumption of transmitting a bit of data can be seen in Eq. (2). All the of parameters are listed in Table 1 [14].

Table 1 Network parameters

2.2 Description of problem

As shown in Fig. 1, the network has two main characteristics. First, the base station is mobile. The base station can move along the black area shown in Fig. 1(a), and the data gathered in the network should be transmitted to the buffer area periodically. When the base station moves in the buffer area, it can gather the data in the buffer area. Buffer area divides the network into two parts ψ₁ and ψ₂. Second, the transmission power of sensor node is variable. The transmission power can be selected in {1, …, k}. When the transmission power is i, the transmission distance is D_i. The key of our research is: how to give the density of sensor nodes in different region in the networks with non-uniform distribution node, so that the entire network can achieve uniform energy consumption and optimal energy efficiency.

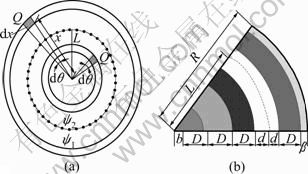
Fig. 1 Network model and parameters buffer area: (a) Buffers ψ₁ and ψ₂; (b) Relationship of R and D

3 Node deployment strategy for mobile base station wireless sensor network

There are a considerable number of researches on optimizing the location of buffer area for mobile base stations wireless sensor network [12, 16]. Therefore, in this work, the optimization location of buffer area used can be got by the algorithm proposed in Refs. [12,16].

Assume that the density of sensor nodes that do undertake data forwarding is ρ, which can meet the lowest requirement of network coverage and monitor performance [17]. The sensor nodes were deployed with different densities in the different regions of network. If the densities of sensor nodes working at the same time are ρ, the entire work can achieve uniform energy consumption by making the sensor nodes whose density is greater than ρ alternating between dormancy and work.

The following theorem shows that when the densities of sensor nodes in different regions of network meet a certain requirement, the entire network can achieve uniform energy consumption (namely the highest energy efficiency of network). That is, when the network lifetime ends, the residual energy of network is zero.

Theorem 1: In the area ψ₁, assume that the density of sensor nodes in the outermost circular ring is ρ, and the density of sensor nodes whose distance from the base station is | i{0, …, w}, x {0, …, D} is  When  meets the requirement of the following expression, the entire network can achieve uniform energy consumption.

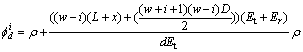
where

             (3)

Proof: The condition of the sensor nodes in the i-th circular ring will be discussed. In the location whose distance from the circular centre is | i{0, …, w}, x {0, …, D}, a segment of circular ring f with a width dx and 2π(L+iD+x)dxf_x sensor nodes will be taken. So, the area of this circular ring is approximately =2π(L+iD+x)dx.

If these sensor nodes are located in the {iD, …, iD+ε}|{0, …w} circular ring, the calculation method of the data amount required to be undertaken by the circular ring φ is given below:

The circular ring φ is responsible for forwarding the data of sensor nodes in the circular rings, which is the integral multiple of D far away from the circular ring φ with a width dx. The area of these regions is given as

             (4)

Assuming that the density of sensor nodes in those regions whose data is received by circular ring is φ and the sensor nodes whose density is greater than ρ alternating between dormancy and work. If the sensor nodes with the density ρ are working at any time, the data amount required to be received by circular φ is shown as

         (5)

The data amount required to be sent is presented as

                                              (6)

Then, each sensor node is required to undertake, the data amount is given as

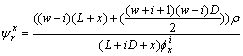              (7)

                                                           (8)

According to Eqs. (1) and (2) of energy consumption, the energy consumption of sensor nodes in this region is given as

E_x=(2+ρ/)E_elec+(+ρ/)ε_fsD²                   (9)

The energy consumption of sensor nodes in the region that are not required to forward data is presented as

E_R=E_elec+ε_fsD²                                                            (10)

To achieve uniform energy consumption of entire network, the equation E_x=E_R should hold. Then:

(11)

Then, Theorem 1 is proven.

Theorem 2: In the area ψ₂, assume that the density of sensor nodes in the innermost circular ring is ρ, and the density of sensor nodes whose distance from the base station is d=L-iD-x, i{0, a}, x{0, …, D} is  When  meets the requirement of following expression, the entire network can achieve uniform energy consumption.

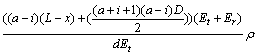(12)

where

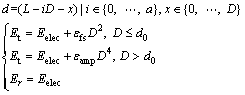
Proof: In the location whose distance from the circular centre is  in the area ψ₂, the segment of circular ring f with a width dx and   sensor nodes will be taken. So, the area of this circular ring is approximately f_s=2π(L- iD-x)dx.

If the sensor nodes are located in the d=L-iD-x, i{0, …, a}, x{0, …, D}, the calculation method of the data amount required to be undertaken by the circular ring f is given below:

The circular ring f is responsible for forwarding the data of all the sensor nodes in the circular rings each of which is the integral multiple of D far away from the circular ring f and with a width dx. The area of these regions is given as

         (13)

Similarly, the data amount that each sensor node is required to undertake is given as

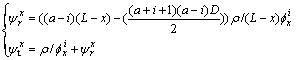(14)

According to Eqs. (1) and (2) of energy consumption, the energy consumption of sensor nodes in this region is given as

E_x=(2+ρ/)E_elec+(+ρ/)ε_fsD²                (15)

The energy consumption of sensor nodes in the region that are not required to forward data is presented as (the density of sensor node is ρ)

E_R=E_elec+ε_fsD²                                                            (16)

To achieve uniform energy consumption of entire network, the equation E_x=E_R should hold.

(17)

Assuming that

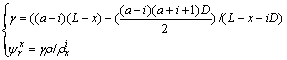(18)

The following expression yields:

                                                   (19)

So, Eq. (12) is obtained.

Theorem 2 is proven.

4 Numerical analysis and simulation

Figure 2 shows that the total nodes amount required to deploy the whole network under different network radii and different node transmission distances with non-uniform node distribution. It can be seen that the decrease of total nodes with the increase of node transmission distance.

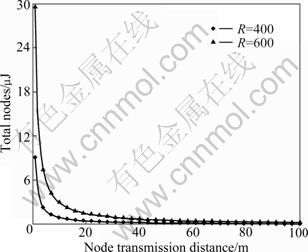
Fig. 2 Total nodes under different transmission distances

Figure 3 shows the ratio of network lifetime to the number of sensor nodes with non-uniform node distribution, and the ratio is referred to as the lifetime efficiency which in fact reflects the effective energy efficiency of sensor nodes. It illustrates that when the same number of sensor node are deployed in some networks, the network with higher lifetime efficiency has longer lifetime. Figure 3 shows the lifetime of network with non-uniform node under different network scales. It is obvious that the larger the network scale is, the lower the lifetime efficiency is. When the transmission distance is 92 m, the lifetime efficiency is the highest. This illustrates that selecting appropriate transmission radius can largely elevate lifetime efficiency.

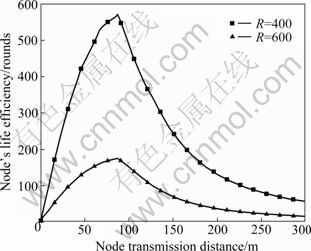
Fig. 3 Ratio of network lifetime for sensor nodes

Figure 4 shows the lifetime of network with uniform node distribution under different transmission radii. Figure 5 illustrates the ratio of the network lifetime to the number of sensor nodes. It is obvious that the network with non-uniform node distribution energy consumption is more efficient than that with uniform node distribution. Figure 6 shows that the ratio of lifetime efficiency with uniform network to non-uniform network. And it can be seen that the efficiency of network with node non-uniform distribution alternating between dormancy and work is higher than the uniform network’s. Moreover, the difference is more obvious with the increase of node transmission radius.

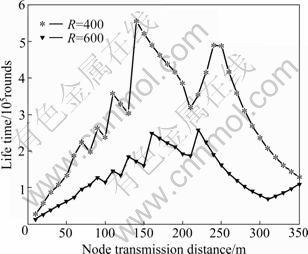
Fig. 4 Lifetime of network under different transmission    radii

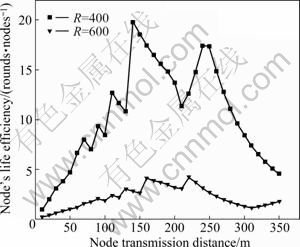
Fig. 5 Ratio of network lifetime for sensor nodes

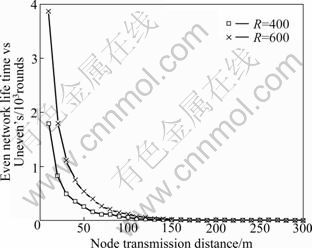
Fig. 6 Ratio of even network lifetime comparing with uneven’s network lifetime

Figures 7 and 8 show that the ratio of node density is related to the parameters E_elec and e_fs, and it may cause inaccurate conclusion if not considered.

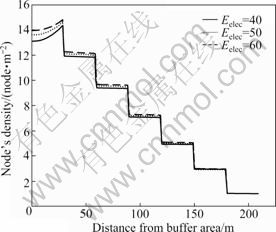
Fig. 7 Node density under different E_elec values

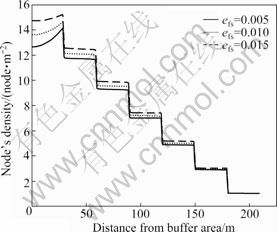
Fig. 8 Node density under different e_fs parameter

5 Conclusions

1) Considering a network scenario where  with mobile base station, a more accurate theoretically analytical method for avoiding energy hole is proposed for wireless sensor network with non-uniform node distribution. And the equations are given for the ratio of node density in different regions.

2) Numerical analysis and simulation prove that the conclusions are right and it presents a better guidance on the optimization of performance for wireless sensor networks.

References

[1] AKYILDIZ I F, SU W, SANKARASUBRAMANIAM Y, CAYIRCI E. Wireless sensor networks: A survey [J]. Computer Networks, 2002, 38(4): 393-422.

[2] LI Jian-zhong, GAO Hong. Survey on sensor network research [J]. Journal of Computer Research and Development, 2008, 45(1): 1-45. (in Chinese)

[3] WANG W, SRINIVASAN V, CHUA K C. Using mobile relays to prolong the lifetime of wireless sensor networks [C]// PORTA T L, LINDEMANN C. Proceedings of the 11th Annual Int’l Conference on Mobile Computing and Networking. New York: ACM Press, 2005: 270-283.

[4] LI J, MOHAPATRA P. An analytical model for the energy hole problem in many-to-one sensor networks [C]// Proceedings 62nd IEEE Vehicular Technology Conference (VTC-Fall ’05). 2005: 2721-2725.

[5] LI J, MOHAPATRA P. Analytical Modeling and Mitigation Techniques for the Energy Hole Problems in Sensor Networks, Pervasive and Mobile Computing, 2007, 3(8): 233-254.

[6] OLARIU S, STOJMENOVIC I. Design guidelines for maximizing lifetime and avoiding energy holes in sensor networks with uniform distribution and uniform reporting [C]// Proceedings of IEEE INFOCOM. Barcelona, Spain, 2006: 1-12.

[7] LIAN J, NAIK K, AGNEW G. Data capacity improvement of wireless sensor networks using non-uniform sensor distribution [J]. International Journal of Distributed Sensor Networks, 2006, 2(2): 121-145.

[8] LIAN J, CHEN L, NAIK K, OTZU T, AGNEW G. Modeling and enhancing the data capacity of wireless sensor networks [C]// IEEE Monograph on Sensor Network Operations, IEEE Press, 2004.

[9] MHATRE V, ROSENBERG C. Design Guidelines for Wireless Sensor Networks: Communication, Clustering and Aggregation, Ad Hoc Networks, 2004.

[10] PERILLO M, CHENG Z, HEINZELMAN W. On the problem of unbalanced load distribution in wireless sensor networks [C]// Proceedings of IEEE GLOBECOM Workshops on Wireless Ad Hoc and Sensor Networks. Dallas, TX, 2004: 74-79.

[11] LIU An-feng, WU Xian-you, CHEN Zhi-gang, GUI Wei-hu. Research on the energy hole problem based on unequal cluster-radius for wireless sensor networks [J]. Computer Communications, 2010, 33(3): 302-321.

[12] SHI Gao-tao, LIAO Ming-hong. Movement-assisted data gathering scheme with load-balancing for sensor networks [J]. Journal of Software, 2007, 18(9): 2235-2244. (in Chinese)

[13] YOUNIS O, FAHMY S. HEED: A hybrid, energy-efficient, distributed clustering approach for ad hoc sensor networks [J]. IEEE Transactions on Mobile Computing, 2004, 3(4): 660-669.

[14] HEINZELMAN W, CHANDRAKASAN A, BALAKRISHNAN H. An application-specific protocol architecture for wireless microsensor networks [J]. IEEE Transactions on Wireless Communications, 2002, 1(4): 660-670.

[15] WU Xiao-bing, CHEN Gui-hai. The energy hole problem of nonuniform node distribution in wireless sensor networks [J]. Chinese Journal of Computers, 2008, 31(2): 1-9. (in Chinese)

[16] LIU An-feng, HE Hui, WU Xian-you, CHEN Zhi-gang. Optimization of parameter selection for wireless sensor network with mobile base station [J]. Journal of Central South University: Science and Technology, 2009, 40(5): 1336-1344. (in Chinese)

[17] LI Ting, LAI Xu-zhi, WU Min. A novel two-swarm based particle swarm optimization algorithm for optimal power flow problem [J]. Journal of Central South University: Science and Technology, 2007, 38(1): 133-137. (in Chinese)

(Edited by DENG Lü-xiang)

Foundation item: Project(60873081) supported by the National Natural Science Foundation of China; Project(NCET-10-0787) supported by Program for New Century Excellent Talents in University; Project(11JJ1012) supported by the Natural Science Foundation of Hunan Province, China

Received date: 2011-06-13; Accepted date: 2011-09-28

Corresponding author: LONG Jun, Associate Professor, PhD; Tel: +86-18673197878; E-mail: jlong@csu.edu.cn