J. Cent. South Univ. (2017) 24: 1529-1536
DOI: 10.1007/s11771-017-3557-y
Statistical design and kinetic and thermodynamic studies of Ni(II) adsorption on bentonite
Bahareh Sadeghalvad, Amir Reza Azadmehr, Hassan Motevaliana
Department of Mining & Metallurgical Engineering, Amirkabir University of Technology, Tehran, Iran  Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: The adsorption of the bentonite toward Ni(II) from aqueous solution was studied to obtain optimum conditions, equilibrium model, thermodynamic and kinetic parameters. Statistical method was used to evaluate maximum amount of adsorbed Ni (II). In this work, pH of solution during stirring, contact time, initial Ni (II) concentration, particle size of bentonite and amount of bentonite were considered as effective parameters which should be examined. The increase of temperature has negative effect on the Ni(II) adsorption. The equilibrium data were correlated well with Freundlich and Dubinin–Radushkevich isotherm models the correlation coefficients of which are (R2) 0.994 and 0.971, respectively. This model indicates heterogeneous and chemical absorption or ion exchange process. The values of thermodynamic parameters such as ΔH°, ΔS° and ΔG° of nickel adsorption reveal that it is a spontaneous, exothermic and associative process. The experimental data fit the pseudo-second-order kinetic very well with correlation coefficient (R2) more than 0.995.
Key words: bentonite; adsorption; experimental design; optimum condition; equilibrium
1 Introduction
Nickel is one of the prominent toxic metal pollutants which is widely discharged into non- biodegradable environment by many industrial activities such as manufacture of super alloys, metal alloys, nickel batteries, steel factories, deposition of ash residues from coal combustion and disposal of municipal sewage sludge [1]. Despite Ni(II) are essential nutrients needed by the body in trace amounts, high concentration (more than 0.02 mg/L) can lead to birth defects, embolism, and chronic bronchitis, vomiting, chest pain, and cancer of lunges, noise and bones [2]. Thus, people suffering from nickel allergy are affected both through nickel-containing diets and skin exposure to nickel-containing materials [3]. It is essential to remove Ni from waste waters, accordingly many processes for Ni(II) removal have been studied, including precipitation, ion exchange, adsorption, coagulation, evaporation and reverse osmosis [4-7]. Generally, these methods have been proved to be costly and it can be produced sludge or mud, which requires proper disposal and confinement [8].
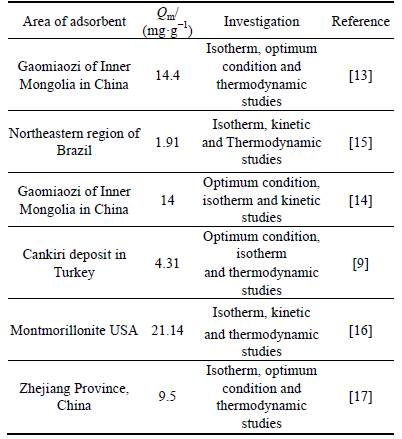
It is obvious that adsorption method especially by clay minerals is one of the significant methods to remove heavy metals from solution. Due to the characteristics of the clay minerals, such as high cation exchange capacity (90-120 meq/100 g), higher elasticity and plasticity, relative low cost, easy handling, abundance adsorbent and easily refine, it has been studied extensively under a wide range of experimental conditions [7, 9-13]. During the last two decades, the use of bentonite for adsorption and removal of Ni(II) ions from solutions have been attractive and many studies have been investigated on optimum conditions, thermodynamics, isotherm models and kinetics [9, 13-17]. The maximum removal of cadmium by bentonite from different places of the world has been summarized in Table 1. The best result is related to montmorillonite from USA with adsorbing 21 mg of nickel per one gram of adsorbent. It has not been observed a reliabile report about the removal of Ni (II) from aqueous solution by Iranian bentonite, therefore this work investigates another usage of Birjand bentonite for adsorption of heavy metals [18]. The main purpose of this work is to optimize adsorption parameters (namely initial Ni concentration, contact time, pH, particle size and mass of bentonite) on Ni uptake from aqueous solution by factorial experimental design, equilibrium models parameters, values of changes Enthalpy, Changes Entropy, Gibbs free energy of nickel adsorption and adsorption reaction order (kinetic study).
2 Methodology
2.1 Materials and methods
Thebentonite sample from the Birjand area in;southeastern of Iran was used without any chemical pretreatment. The samples were ground and sieved by ASTM standard sieves to separate the nominal particle size fractions of 300-400 μm and <150 μm. The Ni (II) concentration after adsorption was determined by means of atomic absorption spectrometry (AAS) of unicom 939. The Ni adsorption was calculated with respect to the amount of Ni in solution.
Table 1 Concise summary of Ni adsorption on bentonite
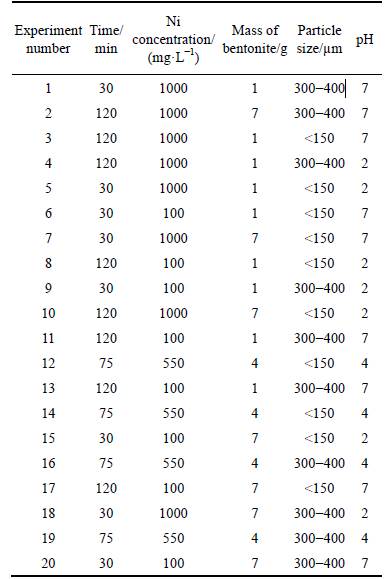
In order to investigate the effect of the initial Ni(II) concentration, contact time, pH, particle size and mass of bentonite Ni(II) adsorption, a factorial experimental designtechnique; using Dx 7 software was employed. 20 experiments recommended by this desgin are defined in Table 2.
Table 2 Experimental results of factorial design for study of five parameters on removal of Ni ions by bentonite
The adsorption isotherms models of Langmuir,Freundlich, Temkin, and Dubinin–Radushkevich (D-R), which their equations are repreasented in Table 3, were studied using 5 g of bentonite added to 100 mL of solution containing different concentrations of Ni, ranging from 10-4 to 2×10-3, contact time 30 min, strring speed of 500 r/m in and pH of 5.5. All of the solutions were immediately filtered after each test.
Table 3 Adsorption isotherm models and equations

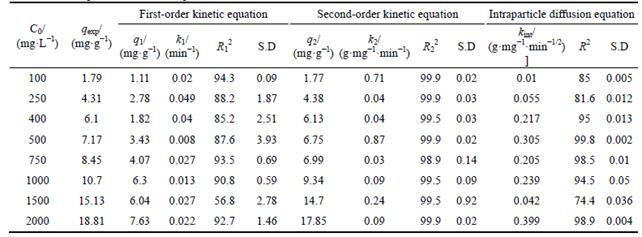
For the kinetic investigation, 5 g of bentonite was mixed with 100 mL of Ni at various concentrations of 100, 250, 400, 500, 750, 1000, 1500 and 2000 mg/L. Each batch test was conducted at various time intervals to determine the period required to reach the adsorption equilibrium and maximum removal of Ni. In order to find out effective processes regarding Ni adsorption onto bentonite, three kinetic equations, pseudo-first-order, pseudo-second-order, and intra-particle diffusion models were examined, as listed in Table 4.
For the thermodynamic investigation, 1, 2, 3, 4 and 5 g of bentonite was added to 100 mL of Ni solution at concentrations of 1000 mg/L and the amount of removed Ni was determined at various temperatures (330, 340, 350 and 360 K). The amount of Ni adsorbed onto bentonite was determined from the difference between the initial and remaining concentrations of solution after adsorption.
3 Result and discussion
3.1 Experimental design
The Design Expert Software was used for experiments design. Factorial design was applied to study and optimize the most important operating factors. Factorial design was used for researching response factors, and it is possible to evaluate their effects. Adsorption experiments were done randomly to avoid errors during data collection. The test conditions and their results are shown in Table 2. As seen in Table 2, time, initial nickel concentration, particle size, absorbent amount and pH are chosen as the six factors to be researched. Two-level factorial design was carried out first to determine which factors and their interactions are significant.
In the statistical design of experiments, the analysis of variance (ANOVA) is a powerful toll for examination of results. It is usual to identify important parameters, significance of their effects and their interactions using ANOVA. In this work, ANOVA shows the nickel concentration, absorbent amount and pH are the most important factors which influence nickel adsorption. The nickel adsorption is increased by increasing absorbent amount, pH and nickel concentration.
In order to visualize the combined effects of the two factors, three-dimensional (3D) plots were used, as shown in Fig. 1. Figure 1(a) shows the interactions between pH and Ni concentration. Nickel adsorption is increased by increasing both pH and nickel concentration. Figure 1(b) shows the effects of pH and solid amount on nickel adsorption. With higher solid amount, nickel adsorption increases and it can be concluded that the effects of solid amount on the nickel adsorption are positive.
In addition, higher solid to liquid ratio or solid content is unfriendly to the filtration. At lower values of solid content, the minimum nickel removal extraction occurs while maximum nickel removal takes place at the maximum solid content.
Table 4 Adsorption kinetic equations

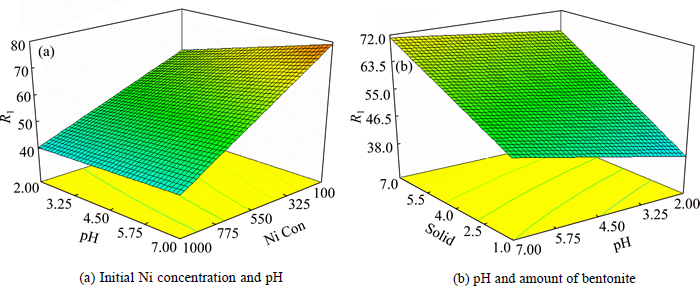
Fig. 1 Surface plot of effects of main variable interactions on Nickle adsorption onto bentonite As can be seen in Fig. 1(b), adsorption amount depends more on the solid amount rather than on pH, although both variables are important.
An optimization technique by design expert software was used for optimization nickel adsorption. In order to optimize this process, the optimum condition where all parameters simultaneously meet the desirable nickel adsorption was investigated. The results are shown in Table 5.
In order to compare model and predicted results, two additional tests are done applying the optimum conditions. The results show that nickel adsorption obtained from the experiments and the predicted values by models are in good agreement.
3.2 Adsorption isotherms
The adsorption isotherm model is used to evaluate the mechanism of adsorption by finding matematical relationship between the amount of nickel adsorbed(q) and nickel equlibrium concentration (Ce) after adsorption process. For this purpose, four different isotherm models (for multilayer and monolayer adsorption surfaces) belonging to category of two parameters are examined.
3.2.1 Langmuir isotherm
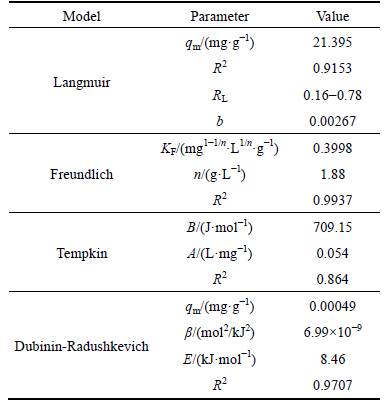
This model assumes that the adsorptive molecules interact with active sites on the bentonite surface which has identical energy that indicates the adsorption occurs onto a homogeneous (uniform) surface with a finite number of adsorption sites. The values of the Langmuir constants b and qm (mg/g) respectively determined by intercept and slope of plot are given in Table 6. The data shows that the maximum adsorptive capacity (21.395 mg/g) of the unmodified Iranian bentonite (from the Birjand area) is considerable according to the earlier workers [13-17]. The equation separation factor (RL) for Langmuir isotherm model is demonstrated in Table 3. It is a dimensionless constant [27, 28]. The range of separation factor (RL) is 0.16 to 0.78 for initial concentrations of Ni (II) between 10-4 and 2×10-3, indicating that isotherms adsorption is favorable because RL is between zero and one. Based on RL values, the adsorption process in high initial Ni(II) concentration is more favorable, but as seen in Fig. 2(a) the linear Langmuir plot with a correlation coefficient (R2) 0.9153 means that the Langmuir model is not able to describe; this adsorption process very well, in other words, experimental data does not prove nickel homogenous adsorption. Therefore, other models are examined to explain nickel adsorption on unmodified bentonite.
3.2.2 Freundlich isotherm
The Freundlich isotherm model describes processes of multilayer adsorption, which is employed to demonstrate heterogeneous system and assumes that the adsorption process is reversible. The slope of the plot of lgq vs lgCe gives the Freundlich isotherm parameter,1/n (l/g), which is described as the heterogeneity factor and n value indicates the degree of non-linearity between; nickel concentration in solution and nickel adsorbed as if 0Figure 2 shows the linear Freundlich plot with R2 of 0.994, indicating that this experimental data is fitted well with Freundlich model. The values of the Freunlich constants KF, n and correlation coefficient are listed in Table 6. The results generated from Freundlich isotherm model represent that nickel adsorption onto Iranian bentonite has been performed by heterogonous favorable adsorption process. 3.2.3 Tempkin isotherm
The linear form of this isotherm model is represented in Table 6. In this model, it is assumed that the binding energy of interaction between adsorbent– adsorbate is uniformly distributed, which causes a linear decrease in the heat of adsorption of all the molecules in the layers [21, 29]. The linear expression of Tempkins’s equation is presented in Table 3. As observed, A and B are determined from the intercept and slope of the linear plots of qe versus lnCe as listed in Table 6, but the correlation coefficient (R2) is 0.864, which demonstrates Tempkin model could not describe Ni(II) adsorption onto bentonite.
3.2.4 Dubinin–Radushkevich (D-R) isotherm
The Dubinin–Radushkevich isotherm describes both homogenous and heterogeneous surface adsorption [30]. So, it is more common than Langmuir and Freundlich isotherm models. It is employed to distinguish physical and chemical adsorptions of metal ions by following equation, which can be applied to calculate the free energy per molecule of adsorbate (E) [22].
Table 5 Verification experiments at optimum conditions

Table 6 Langmuir, Freundlich, Tempkin and Dubinin– Radushkevich isotherm constants for Ni adsorption onto bentonite
 (1)
(1)
If the value of adsorption energy (E) is less than 8 kJ/mol, physical adsorption governs the reaction; chemical absorption or ion exchange is most important if the adsorption energy is between 8 and 16 kJ/mol, and for E value more than 16 kJ/mol, particle diffusion dominates [22, 31].
Linear plots of lnqe versus ln2(1+c-1) with R2 of 0.971 are observed in Fig. 2. The conditions are pH 5.5, Ni concentration of 50 g/L, temperature of 298K, particle size<150 μm, stirring speed of 500 r/min, and contact time of 30 min. The parameters qm and Β are calculated from the intercepts and slopes, respectively. The adsorption free energy (E) is 8.46 kJ (Table 6), which means that adsorption of Ni(II) by bentonite is a chemical absorption or ion exchange process.
3.2.5 Evaluation of adsorption isotherm models of Ni onto bentonite
To sum up, in these four isotherm models, Freundlich and D-R isotherm models have the highest R2 value, so these two models cover the adsorption data better than Langmuir and Tempkin models, which proves that the adsorption of Ni(II) onto bentonite is a heterogeneous (multilayer surface) process and it is indicated that Ni(II) is adsorbed to bentonite through a chemical process.
The kinetic of adsorption process considering the effect of contact time and initial Ni(II) concentration to reach the equilibrium adsorption describes the reaction pathways and rate of adsorption [32].
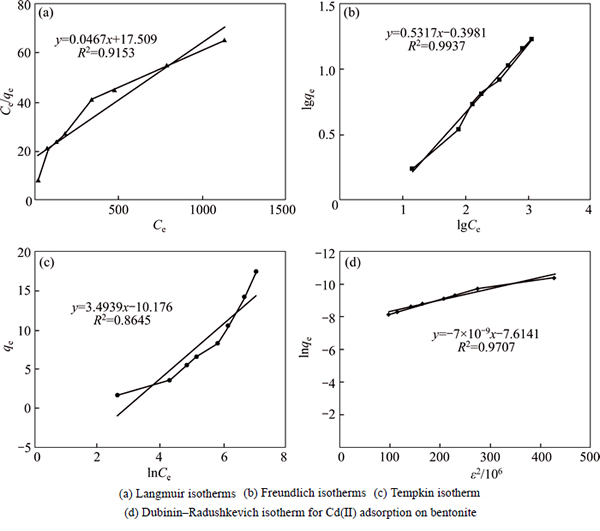
Fig. 2 Linear plots of lnqe versus ln2(1+c-1) with R2 of 0.971; Adsorption kinetics shows large dependence on the physical and/or chemical characteristics of the sorbent material, which also influences the adsorption mechanism.
In order to investigate the mechanism of Ni(II) adsorption onto Iranian bentonite according to Fig. 3, the amount of Ni (II) adsorbed in various initial Ni concentration versus contact time, has been examined. It shows that Ni (II) adsorbed increases with increasing contact time and reaches equilibrium (constant value) after 60 min. It is obvious that the physical and chemical characteristics of the bentonite greatly affect the nickel adsorption.
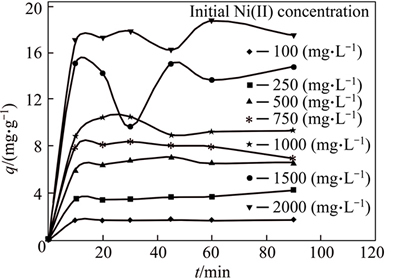
Fig. 3 Adsorption kinetics of Ni(II) on bentonite at different initial Ni(II) concentrations Three different models pseudo-first-order, pseudo-second-order, and intra-particle diffusion models have been studied to find the mechanism of nickel adsorption.
The pseudo-first order rate equation for the liquid-solid adsorption system was expressed by Lagergren’s original paper expressed in 1898 [23], the equation of which is represented in Table 4. The rate constant of adsorption is determined by slop of plot ln(qe-qt) versus t (time). Pseudo-second order reaction model is based on sorption equilibrium capacity [24], that both adsorbate and adsorbent have controlled the rate of adsorption. In intra particle diffusion model, the rate of adsorption is limited by diffusion of intra particles presented in 1963 by WEBER et al [33] to describe the adsorption on carbon particles. The intraparticle model is presented by plot of qt (amount of nickel adsorbed at time t) versus t1/2. All equations of these models are presented in Table 4.
Three different models have been examined to identify which model is fitted well, the experimental data of nickel ions adsorbed on bentonite and nickel ions adsorbed at equilibrium state calculated from linear expression of model equations are compared.
As seen in Table 7, the values of the different parameters of each model are calculated from the linear equations, where SD denotes standard deviation, subscript “exp” denotes experiment. With respect to the R2 values of plots (>99.5) describing for the experimental results at different initial Ni concentrations, the pseudo second-order adsorption mechanism is predominant in these experiments. In other words, the R2 and standard values for the pseudo-second- order equation are better than those of the pseudo- first-order and intra-particle diffusion models therefore the rate-controlling step is chemisorption interaction. This means that both the concentration of adsorbate (Ni(II) ions) and the number of active bentonite sites affect the adsorption mechanism and the rate of adsorption.
The thermodynamics measurements of Ni adsorption onto bentonite are performed in 1000 mg/L Ni(II) at 330, 340, 350 and 360 K. Thermodynamic parameters can be explained by [35]:
 (2)
(2) 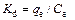 (3)
(3)
where qe (mg/g) is the amount of adsorbed Ni (II),
Table 7 Kinetic parameters for adsorption of Ni onto bentonite
C0(mg/L) is the initial Ni (II) concentration, Ce(mg/L) is the equilibrium Ni concentration in solution after Ni (II) absorbed by bentonite, m(g) is the mass of bentonite used and V(L) is the volume of solution . The distribution coefficient (Kd) values are used in the following equation to determine the Gibbs free energy of sorption process at different temperatures.
 (4)
(4) where ΔG° is the free energy change of Ni adsorption (kJ/mol), R is the universal gas constant (8.314 J/mol·K), and T is the absolute temperature of solution during adsorption process (K). The adsorption distribution coefficient may be expressed in terms of enthalpy change (ΔH°) which is the heat of adsorption (kJ/mol) and the standard entropy change of adsorption (ΔS°) (kJ/mol) which is a function of temperature [34, 35]:
 (5)
(5) According to Eq. (5), the values of ΔHo and ΔSo are determined from the slopes and intercept of the plot of lnKd vs (1/T) (Fig. 3) and demonstrated in Table 8. The negative value of ΔH° (-51.561 kJ/mol)) indicates exothermic nature of adsorption, which means that with increasing temperature, adsorption of Ni onto bentonite decreases. The literature survey ΔHo absolute value is 40-120 kJ/mol and otherwise these values occur chemisorptions and physisorption, respectively. Therefore, the heat of adsorption obtained from this process shows that Ni(II) adsorption onto Iranian betonite is chemical interaction. The negative value of entropy changes (ΔS°) reflects a decreasing solution interface during adsorption. In other words, it is associative interaction, of course the negative value of entropy changes (ΔS°) is logical because the adsorption process causes the numbers of ions in the solution to decrease. These enthalpy changes (ΔH°) and entropy changes (ΔS°) are considerable when compared with other research because against thermo dynamical values of this work, many researchers have reported that nickel; adsorption onto bentonite is endothermic and dissociative process [14-17] that this observation is an indication of Iranian bentonite with especial properties at nickel adsorption. The negative value of ΔG° at 330- 360 K indicates that nickel adsorption is spontaneous. In other words, no external energy (from outside of system) is required to perform adsorption process. As observed in Fig. 4, with increasing temperature, the value of ΔG° decreases indicating Ni(II) ion adsorption is less favorable at higher temperature which emphasizes that it is an exothermic process.
Table 8 Thermodynamic parameters for adsorption of Ni onto bentonite

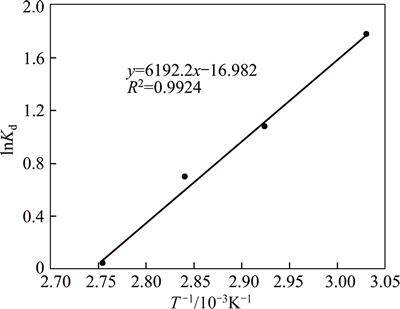
Fig. 4 Plot of lnKd vs 1/T to determine enthalpy and entropy of adsorption reaction 4 Conclusions
Iranian bentonite from Birjand area shows the ability for adsorption of Ni(II) that the maximum amount of adsorbed Ni(II) is obtained at conditions of pH of 6, solid to liquid ratio of 70 g/L, temperature of 298 K, particle size of <150 mm, stirring speed of 500 r/min, contact time of 30 min, which is determined by design expert. The results of experiment are fitted with Frendlich and Dubinin–Radushkevich (D-R) isotherm models correlation coefficient (R2) 0.904 and 0.971, respectively, indicating a maximum adsorption capacity of 21.39 mg/g. From ΔS° (entropy changes), ΔH° (enthalpy) and ΔG° (Gibbis free energy) values at 330-360 K, it can be concluded that exothermic, associative and spontaneous processes dominate in Ni(II) adsorption. The time data of adsorption follows the pseudo second order rate equation, indicating adsorption process rate on the surface of bentonite is controlled by rate-determining step.
References
[1] AJMAL M, RAO R A K, AHMAD R, AHMAD J. Adsorption studies on Citrus reticulata (fruit peel of orange): removal and recovery of Ni(II) from electroplating wastewater [J]. Journal of Hazardous Materials, 2000, 79(1): 117-131.
[2] KADIRVELU K, P SENTHILKUMAR, THAMARAISELVI K AND SUBBURAM V. Activated carbon prepared from biomass as adsorbent: Elimination of Ni(II) from aqueous solution [J]. Bioresource Technology, 2002, 81(1): 87-90.
[3] Mc GRATH S, SMITH S. Chromium and nickel [J]. Heavy Metals in Soils, 1995, 7: 152-178.
[4] AJMAL M, MOHAMMAD A, YOUSUF R, AHMAD A. Adsorption behaviour of cadmium, zinc, nickel and lead from aqueous solutions by Mangifera indica seed shell [J]. Indian Journal of Environmental Health, 1998, 40(1): 15-26.
[5] GUPTA V K, JAIN C, ALI I, SHARMA M, SAINI V. Removal of cadmium and nickel from wastewater using bagasse fly ash—A sugar industry waste [J]. Water Research, 2003, 37(16): 4038-4044.
[6] POPURI S R, VIJAYA Y, BODDU V M, ABBURI K. Adsorptive removal of copper and nickel ions from water using chitosan coated PVC beads [J]. Bioresource Technology, 2009, 100(1): 194-199.
[7] ABOLLINO O, ACETO M, MALANDRINO M, SARZANINI C, MENTASTI E. Adsorption of heavy metals on Na-montmorillonite: Effect of pH and organic substances [J]. Water Research, 2003, 37(7): 1619-1627.
[8] RHAZI M, DESBRIERES J, TOLAIMATE A, RINAUDO M, VOTTERO P, ALAGUI A. Contribution to the study of the complexation of copper by chitosan and oligomers [J]. Polymer, 2002, 43(4): 1267-1276.
[9] DONAT R, AKDOGAN A, ERDEM E, CETISLI H. Thermodynamics of Pb2+ and Ni2+ adsorption onto natural bentonite from aqueous solutions [J]. Journal of Colloid and Interface Science, 2005, 286(1): 43-52.
[10] TAHIR S, RAUF N. Thermodynamic studies of Ni (II) adsorption onto bentonite from aqueous solution [J]. The Journal of Chemical Thermodynamics, 2003, 35(12).
[11] FUTALAN C M, KAN C C, DALIDA M L, HSIEN K J, PASCUA C, WAN M W. Comparative and competitive adsorption of copper, lead, and nickel using chitosan immobilized on bentonite [J]. Carbohydrate Polymers, 2011, 83(2): 528-536.
[12] BHATTACHARYYA K G, GUPTA S S. Influence of acid activation on adsorption of Ni(II) and Cu(II) on kaolinite and montmorillonite: kinetic and thermodynamic study [J]. Chemical Engineering Journal, 2008, 136(1): 1-13.
[13] LIU Z R, ZHOU S Q. Adsorption of copper and nickel on Na-bentonite [J]. Process Safety and Environmental Protection, 2010, 88(1): 62-66.
[14] YANG S, LI J, LU Y, CHEN Y, WANG X. Sorption of Ni (II) on GMZ bentonite: Effects of pH, ionic strength, foreign ions, humic acid and temperature [J]. Applied Radiation and Isotopes, 2009, 67(9): 1600-1608.
[15] VIEIRA M, NETO A, GIMENES M, DA SILVA M. Sorption kinetics and equilibrium for the removal of nickel ions from aqueous phase on calcined Bofe bentonite clay [J]. Journal of Hazardous Materials, 2010, 177(1): 362-371.
[16] GUPTA S S, BHATTACHARYYA K G. Adsorption of Ni (II) on clays [J]. Journal of Colloid and Interface Science, 2006, 295(1): 21-32.
[17] XU D, ZHOU X, WANG X. Adsorption and desorption of Ni2+ on Na-montmorillonite: Effect of pH, ionic strength, fulvic acid, humic acid and addition sequences [J]. Applied Clay Science, 2008, 39(3): 133-141.
[18] SADEGHALVAD B, ARMAGHAN M, AZADMEHR A. Using iranian bentonite (Birjand Area) to remove cadmium from aqueous solutions [J]. Mine Water and the Environment: 1-10.
[19] LANGMUIR I. The adsorption of gases on plane surfaces of glass, mica and platinum [J]. Journal of the American Chemical society, 1918, 40(9): 1361-1403.
[20] THAMILARASU P, KARUNAKARAN K. Kinetic, equilibrium and thermodynamic studies on removal of Cr (VI) by activated carbon prepared from Ricinus communis seed shell [J]. The Canadian Journal of Chemical Engineering, 2013. 91(1): 9-18.
[21] CRINI G, PEINDY H N, GIMBERT F, ROBERT C. Removal of CI Basic Green 4 (Malachite Green) from aqueous solutions by adsorption using cyclodextrin-based adsorbent: Kinetic and equilibrium studies [J]. Separation and Purification Technology, 2007, 53(1): 97-110.
[22] OZCAN A S, ERDEM B, OZCAN A. Adsorption of Acid Blue 193 from aqueous solutions onto BTMA-bentonite [J]. Colloids and Surfaces-A-Physiochemical and Engineering Aspects, 2005, 266(1-3): 73-81.
[23] YUH-SHAN H. Citation review of Lagergren kinetic rate equation on adsorption reactions. [J]. Scientometrics, 2004, 59(1): 171-177.
[24] HO Y S, Mc KAY G. Pseudo-second order model for sorption processes [J]. Process Biochemistry, 1999, 34(5): 451-465.
[25]  Equilibrium and kinetic modelling of adsorption of phosphorus on calcined alunite [J]. Adsorption, 2003, 9(2): 125-132.
Equilibrium and kinetic modelling of adsorption of phosphorus on calcined alunite [J]. Adsorption, 2003, 9(2): 125-132.
[26] JUANG R S, TSENG R L, WU F C, LEE S H. Adsorption behavior of reactive dyes from aqueous solutions on chitosan [J]. Journal of Chemical Technology and Biotechnology, 1997, 70(4): 391-399.
[27] FREUNDLICH H. Over the adsorption in solution [J]. J phys Chem, 1906, 7(385471): 1100-1107.
[28] TEMKIN M, PYZHEV V. Kinetics of ammonia synthesis on promoted iron catalysts [J]. Acta Physiochim, URSS, 1940, 12(3): 217-222.
[29] KIM Y, KIM C, CHOI I, RENGARAJ S, YI J. Arsenic removal using mesoporous alumina prepared via a templating method [ Environmental science & technology, 2004. 38(3): 924-931.
[30] SHAHWAN T, ERTEN H. Temperature effects in barium sorption on natural kaolinite and chlorite-illite clays [J]. Journal of Radioanalytical and Nuclear Chemistry, 2004, 260(1): 43-48.
[31] ONYANGO M S, KOJIMA Y, AOYI O, BERNARDO E C, MATSUDA H. Adsorption equilibrium modeling and solution chemistry dependence of fluoride removal from water by trivalent- cation-exchanged zeolite F-9 [J]. Journal of Colloid and Interface Science, 2004, 279(2): 341-350.
[32]  ,
,  , KARA S. Kinetic and equilibrium studies in removing lead ions from aqueous solutions by natural sepiolite [J]. Journal of Hazardous Materials, 2004, 112(1): 115-122.
, KARA S. Kinetic and equilibrium studies in removing lead ions from aqueous solutions by natural sepiolite [J]. Journal of Hazardous Materials, 2004, 112(1): 115-122.
[33] WEBER W, MORRIS J. Kinetics of adsorption on carbon from solution [J]. J Sanit Eng Div Am Soc Civ Eng, 1963, 89(17): 31-60.
[34] JAMAN H, CHAKRABORTY D, SAHA P. A study of the thermodynamics and kinetics of copper adsorption using chemically modified rice husk [J]. CLEAN–Soil, Air, Water, 2009. 37(9): 704-711.
[35] HO Y S. Removal of copper ions from aqueous solution by tree fern [J]. Water Research, 2003, 37(10): 2323-2330.
(Edited by FANG Jing-hua)
Cite this article as: Bahareh Sadeghalvad, Amir Reza Azadmehr, Hassan Motevalian. Statistical design and kinetic and thermodynamic studies of Ni (II) adsorption on bentonite [J]. Journal of Central South University, 2017, 24(7): 1529-1536. DOI: 10.1007/s11771-017-3557-y.
Received date: 2016-03-08; Accepted date: 2016-12-23; Corresponding author: Amir Reza Azadmehr; Tel: +98-9124195819; E-mail: A_azadmehr@aut.ac.ir