文章编号：1004-0609(2007)03-0446-07

高拉速连铸结晶器的非正弦振动振幅

孟祥宁¹，朱苗勇¹，程乃良²，江中块²

(1. 东北大学 材料与冶金学院，沈阳 110004;

2. 上海宝钢集团 梅山钢铁股份有限公司，南京 210039)

摘  要：利用结晶器传热模型、热/应力模型和现场数据，建立了结晶器内液体摩擦力计算模型，利用该模型分析了某钢厂2.0 m/min拉速下结晶器非正弦振动振幅对液体摩擦力的影响，给出了振幅选取原则和确定方法。结果表明：拉速一定时采用小振幅振动可限制最大液体摩擦力，增大保护渣耗量，减小负滑脱时间，随拉速提高应适当增大振幅，以改善振动效果；结合现场工艺，确定拉速2.0 m/min时的适宜振幅为±4 mm，拉速升至2.2 m/min，振幅相应增至±4.5 mm；保护渣膜厚度计算结果符合生产实际，为研究结晶器内润滑机理提供了条件。

关键词：连铸结晶器；非正弦振动；振幅；液体摩擦力；保护渣膜；润滑

中图分类号：TF 777　　     文献标识码：A

Non-sinusoidal oscillation amplitude for continuous casting mold with high casting speed

MENG Xiang-ning¹, ZHU Miao-yong¹, CHENG Nai-liang², JIANG Zhong-kuai²

(1. School of Materials and Metallurgy, Northeastern University, Shenyang 110004, China;

2. Meishan Iron and Steel Co. Ltd., Shanghai Baosteel Co., Nanjing 210039, China)

Abstract: A mathematical model to the represent liquid flux friction in mold was established by heat-transfer model, heat-stress model and actual data. The effect of non-sinusoidal oscillation amplitude on liquid friction force was analyzed at casting speed of 2.0 m/min, the selection principle and determination method of amplitude were also introduced. The results show that the small amplitude application at certain casting speed can restrict the maximal liquid friction force, increase the flux consumption and decrease the negative strip time. The amplitude should be suitably increased with casting speed to improve the ameliorate oscillation effect. Combined with the casting production, the optimum amplitudes casting speed of 2.0 m/min and 2.2 m/min are obtained as ±4 mm and ±4.5 mm, respectively. The flux film thickness that accords with the practical condition commendably provides guidance to study the mold lubrication mechanism.

Key words: continuous casting mold; non-sinusoidal oscillation; amplitude; liquid friction force; flux film; lubrication

连铸结晶器内摩擦力对生产率和铸坯质量影响显著，而结晶器非正弦振动作为实施高效连铸的关键技术，可有效改善润滑、减小摩擦，因此对结晶器振动参数的研究值得关注。研究表明^[1-7]：结晶器内摩擦力分为液体渣膜中由黏性牛顿流体产生的液体摩擦力和结晶器壁与固体渣膜间库仑摩擦产生的固体摩擦力，总摩擦力为二者之和；结晶器不同部位摩擦状况不同，上部以液体摩擦为主，下部以固体摩擦为主；弯月面初凝壳较薄，是振痕和表面缺陷发生源；固体摩擦力与钢水静压力成正比，连铸过程中变化不大；摩擦力变化规律与结晶器振动波形一致；优化振动参数能改善振动效果。在此基础上，结合李宪奎等^[8]提出的振动参数的确定应是随拉速变化的动态选择，利用建立的结晶器传热模型、热/应力模型和实际数据建立了液体摩擦力计算模型，利用该模型分析了非正弦振动振幅对液体摩擦力的影响，给出振幅选取原则和确定方法，确定了适合生产的最佳振幅，阐明了振幅随拉速提高的变化规律，为优化振动参数、建立振动同步控制关系和最大限度发挥连铸机潜能提供依据。

1  液体摩擦力计算模型

1.1  结晶器传热模型

结晶器热面温度通过传热模型计算得到。图1所示为结晶器结构示意图，x，y，z轴分别平行于结晶器宽面、窄面和拉坯方向，坐标原点位于结晶器出口。

铸坯、铜板和冷却水间传热非常复杂，计算中作以下假设：1) 铜板导热系数为各向同性，密度和比热容为常数；2) 介质间为稳态传热；3) 结晶器内传热对称；4) 忽略水缝冷却水的核态沸腾。

结晶器内传热控制方程为^[9]

其中，对流换热系数由以下经验式确定^[10-11]：

1.2  结晶器热/应力模型

结晶器铜板变形量由热/应力模型计算，坐标系如图1。假设：1) 铜板与背板结合紧密，忽略螺栓对铜板作用力；2) 铜板和背板的力学和热性能为各向同性；3) 背板温度低，刚性强于铜板，考虑背板和铜板分别具有弹性和弹塑性。

图1  结晶器结构示意图

Fig.1  Schematic diagrams of mold structure (mm): (a) Transverse plane of wide face; (b) Longitudinal plane of water slots

热弹性应力/应变方程为

1.3  气隙宽度的计算

计算结晶器内气隙作假设：1) 铸坯垂直拉坯方向为稳态传导传热，沿拉坯方向传热为零；2) 坯壳温度沿传热方向线性分布；3) 忽略凝固相变引起的坯壳力学行为；4) 坯壳为不可压缩材料，不考虑钢水静压力；5) 弯月面受传热和渣道压力影响稳定，形状不变。

弯月面下h处的气隙宽度为^[13-14]

铸坯表面温度由现场仿真系统采集，h处坯壳节点温度由式(6)和(7)计算，取n′=10。

1.4  液体渣膜厚度的计算

渣道宽度一般在10^-2~10^-1­­­ mm范围内^[15]，随结晶器往复振动渣道内产生一定压力，而结晶器下部固体渣膜增厚，以固体摩擦为主，液体渣膜厚度增幅小，同时结晶器热面温度由冷却水温差建立的热平衡关系求得，与导热系数无关，则为计算简便，忽略实际存在的微小气隙，假设保护渣充满整个气隙，渣膜内温度线性分布。

h处渣膜内温度梯度和液体渣膜厚度为

1.5  液体摩擦力的计算

假设保护渣熔化速度满足消耗且稳定流动，h处单位面积液体摩擦力为^{[5, 16]}

v_m遵循图2中具有最佳振动模式特点的非正弦振动波形^[17]，波形曲线由直线段bc、抛物线段cd、余弦曲线段deg、抛物线段gj和直线段jl依次光滑连接，解析式如式(11)所示，式(12)~(15)为过程参数表达式。

图2  非正弦振动速度曲线

Fig.2  Non-sinusoidal oscillation speed curve

2  计算结果及分析

图2所示曲线具有对称性，只计算v_m遵循bc段、cd段和de段规律时振幅对液体摩擦力的影响，钢种为实际生产的SPHC(C含量小于0.08%)，数据见表1、表2。

表1  金属材料及冷却水热属性

Table 1  Thermal properties of metal materials and cooling water

表2  工艺操作和物性参数

Table 2  Operating parameters and flux properties

2.1  渣膜厚度计算结果

图3所示为渣膜厚度计算结果。线性收缩系数δ_h在h为130 mm(1 300 ℃)处的较大变化使d_l和d_z陡增，导致图4~6中p_l值均有明显改变；d_l和d_z在弯月面区为较薄的0.06~0.09 mm和0.20~0.32 mm，d_z受铸坯表面温度影响大，受较低的结晶器热面温度影响小，沿拉速方向d_z不断增厚，到结晶器出口达5.0 mm，与结晶器窄面226 mm、冷坯210 mm的实际情况吻合；h小于320 mm，初凝区坯壳与冷却水温差大，坯壳收缩产生气隙，热阻增大，温度较高，d_l呈上升趋势，而h在260~300 mm范围内，铜板变形量u_c较大，传热状况改变，d_l变化不明显，h大于320 mm，铸坯表面温度降低是d_l下降的主要原因；d_l/d_z值为0.08~0.30，总体呈下降趋势，主要受铸坯表面温度的影响，只在u_c波动较大、h为300~320 mm时略为上升。

图3  渣膜厚度计算结果

Fig.3  Results of liquid and total flux film thickness

2.2  直线段液体摩擦力

图4所示为bc段液体摩擦力计算结果。结晶器以速度v上振，沿拉速方向，d_l增大，使p_l下降，结晶器上部以液体摩擦为主，相同h处，随振幅增加，p_l增大，初凝区振幅由1 mm增至10 mm，p_l可由100 Pa增至340 Pa，采用小振幅可限制p_l增大，小振幅还能加大保护渣耗量，改善润滑，有利于减少因拉速提高引起的表面缺陷。

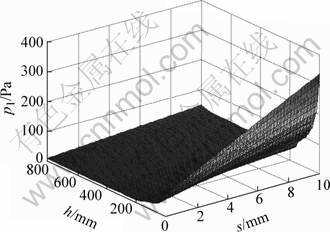
图4  bc段液体摩擦力

Fig.4  Liquid friction force in bc section

2. 3  抛物线段瞬态液体摩擦力

抛物线周期f₁^-1由振动频率决定，振频145 min^-1时，t_cd为0.052 s，t_cd内液体摩擦力变化与振动波形一致，呈下降趋势，取进入曲线cd段后0.03 s作为研究振幅与液体摩擦力关系的瞬态时刻。图5所示为cd段的液体摩擦力计算结果。图中振幅与瞬态液体摩擦力的关系与图4所示一致，只是相同h处的p_l值稍小，采用小振幅可限制液体摩擦力和改善润滑状况。

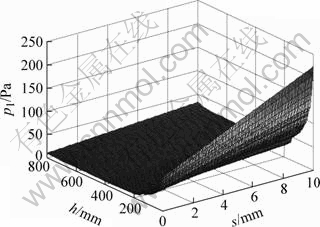
图5  cd段瞬态液体摩擦力

Fig.5  Transient liquid friction force in cd section

2.4  余弦曲线段瞬态液体摩擦力

v_m按de段规律变化，振动经历正滑脱dp段和负滑脱pe段，振频145 min^-1时，0.009 3 s≤t_de-0.5t_N≤0.056 5 s，取进入de段后0.005 s和0.065 s分别作为研究正、负滑脱段振幅对液体摩擦力影响的瞬态时刻。图6(a)中p_l为正值，振动处于正滑脱段，v_m和v_c方向一致，相同h处，振幅增加使p_l值下降，范围较小，为20~70 Pa；拉速提高时，仍可采用小振幅，限制正滑脱相对速度差v_d增大，同时正滑脱时间增加，润滑改善。图6(b)中p_l为负值，振动进入负滑脱段，铸坯表面承受压应力，初凝区p_l变化明显，振幅由2 mm增至10 mm，p_l由20 Pa增至400 Pa，负滑脱量也明显增大，但随振幅增大，负滑脱时间和v_d增加，正滑脱时间减少，不利于改善振动效果，应在保证合适负滑脱段压应力和负滑脱量前提下，采用小振幅。

图6  de段瞬态液体摩擦力

Fig.6  Transient liquid friction force in de section: (a) In dp section; (b) In pe section

2.5  振幅的确定

振动采用小振幅能增加保护渣耗量，限制最大液体摩擦力和正滑脱相对速度差，减小负滑脱时间，但也降低了负滑脱量和负滑脱段铸坯表面压应力，而铸坯表面缺陷主要由正滑脱段液体摩擦力引起，负滑脱段给予的愈合只是补救。因此，降低正滑脱液体摩擦力、增加保护渣耗量，兼顾负滑脱时间和负滑脱量应是选取最佳振幅的基本原则。

现场适宜保护渣耗量为0.32~0.39 kg/m²，由经验式(16)得振幅选取范围为1.98~9.76 mm。

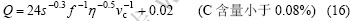
为控制振痕深度并维持一定负滑脱量，合理低碳钢负滑脱时间为0.1~0.12s。由式(12)负滑脱时间0.1 s和0.12 s分别对应振幅3.02 mm和4.19 mm，根据预防为主原则，选取小振幅±4 mm。由图4和图6(b)可知，该振幅下正滑脱最大液体摩擦力小于180 Pa，瞬态负滑脱压应力近120 Pa，铸坯表面承受一定压应力，此时保护渣耗量、负滑脱时间、负滑脱量和正滑脱相对速度差分别为0.361 kg/m²、0.118 s、3.267 mm和4.25 m/min。

拉速提高导致保护渣耗量、负滑脱时间和负滑脱量均下降，采用小振幅虽可限制最大液体摩擦力，增大正滑脱时间，增加保护渣耗量，却使负滑脱时间进一步减少，为表征负滑脱时间引入控制参量Z(Z=2s/v_c)，得图7所示的非正弦振动因素0.2时的负滑脱时间曲线族，拉速2.0 m/min时，Z值为4，为保证拉速升至2.2 m/min后负滑脱时间稳定，即Z值恒定，应使振幅增至±4.5 mm。此时保护渣耗量、负滑脱量和正滑脱相对速度差为0.344 kg/m²、3.774 mm和4.73 m/min，保护渣耗量控制在合适范围，负滑脱量显著增大，有利于铸坯脱模和裂纹愈合。若所得振幅不理想，则重复上述过程，直至合适。值得指出，这里正滑脱相对速度差有所增大，实际操作中可通过其他措施补偿(降低振频f或增大非正弦振动因素α)，振幅选取还应结合振频和非正弦振动因素等综合考虑。

图7  负滑脱时间曲线

Fig.7  Negative strip time curves

3  结论

1) 一定拉速下，结晶器采用小振幅振动可限制最大液体摩擦力，增大保护渣耗量，减小负滑脱时间，有利于改善铸坯表面质量。随拉速提高振幅应适当增加，以维持一定的负滑脱时间，增大负滑脱量，并控制保护渣耗量在合理范围。

2) 振幅选取原则和确定方法为指导生产提供了依据。结合现场实际，选取拉速2.0 m/min时最佳振幅±4 mm，拉速升至2.2 m/min，振幅增至±4.5 mm。选定振幅下保护渣耗量、负滑脱时间均控制在合适范围。

3) 渣膜厚度受铸坯表面温度和铜板变形量等因素影响，在结晶器不同部位呈现不同的变化趋势。渣膜厚度计算结果符合生产实际，为深入研究结晶器内润滑机理提供了条件。

REFERENCES

[1] 干 勇，陈栋梁，杨文改. 连铸结晶器瞬态摩擦阻力的实验研究[J]. 钢铁，1999，34(4): 16-19.

GAN Yong, CHEN Dong-liang, YANG Wen-gai. The experimental study of the mould dynamic friction force in continuous casting of steel[J]. Iron and Steel, 1999, 34(4): 16-19.

[2] 姚 曼，王文华，魏树立，等. 板坯连铸结晶器摩擦力计算与影响因素研究[J]. 大连理工大学学报，2002，42(2): 195-199.

YAO Man, WANG Wen-hua, WEI Shu-li, et al. Study of calculation and affecting parameters of mold friction in slab continuous casting[J]. Journal of Dalian University of Technology, 2002, 42(2): 195-199.

[3] Edward S. Overview of mold oscillation in continuous casting[J]. Iron and Steel Engineer, 1996, (7): 29-37.

[4] Darle T, Mouchette A, Nadif M, et al. Hydraulic oscillation of the CC slab mold at sollac florange: First industrial results, future developments[J]. Steelmaking Conference Proceedings, 1993: 209-218.

[5] 李宪奎，张德明. 连铸结晶器振动技术[M]. 北京：冶金工业出版社，2000.

LI Xian-kui, ZHANG De-ming. Continuous Casting Mold Oscillation Technology[M]. Beijing: Metallurgical Industry Press, 2000.

[6] Kwon O D, Choi J, Lee I R, et al. Optimization of mold oscillation pattern for the improvement of surface quality and lubrication in slab continuous casting[J]. Steelmaking Conference Proceedings, 1991: 561-568.

[7] Araki T, Ikeda M. Optimization of mold oscillation for high speed casting—New criteria for mold oscillation[J]. Canadian Metallurgical Quarterly, 1999, 38(5): 295-300.

[8] 李宪奎，于敏之，赵红雁. 结晶器反向振动同步控制模型[J]. 重型机械，2001(2): 16-19.

LI Xian-kui, YU Min-zhi, ZHAO Hong-yan. Inverse oscillation synchro-control model[J]. Heavy Machinery, 2001(2): 16-19.

[9] Thomas B G, Li G, Moitra A, et al. Analysis of thermal and mechanical behavior of copper molds during continuous casting of steel slabs[J]. Steelmaking Conference Proceedings, 1997, 80: 183-201.

[10] Akira Y, Toshihiko E, Seshadri S. A Mathematical model for prediction of thickness of mould flux film in continuous casting mould[J]. ISIJ International, 2002, 42(10): 1084-1093.

[11] Joong K P, Indira V S, Brian G T, et al. Analysis of thermal and mechanical behavior of copper mould during thin slab casting[J]. Steelmaking Conference Proceedings, 2000, 83: 9-21.

[12] Thomas B G. Issues in thermal-mechanical modeling of casting processes[J]. Iron and Steel Institute of Japan International, 1995, 35(6): 737-743.

[13] 张玉文，朱立光，丁伟中. 连铸保护渣润滑行为的数学模拟[J]. 钢铁研究学报，2002，14(4): 21-25.

ZHANG Yu-wen, ZHU Li-guang, DING Wei-zhong. Mathematical simulation on lubrication behavior of mold flux[J]. Journal of Iron and Steel Research, 2002, 14(4): 21-25.

[14] 朱立光，王硕明，金山同. 连铸结晶器内保护渣渣膜状态的数学模拟[J]. 北京科技大学学报，1999，21(1)：13-16.

ZHU Li-guang, WANG Shuo-ming, JIN Shan-tong. Mathematical simulation for state film in C.C. mold[J]. Journal of University of Science and Technology Beijing, 1999, 21(1): 13-16.

[15] 雷作胜，任忠鸣，阎勇刚，等. 软接触结晶器电磁连铸保护渣道的动态压力[J]. 金属学报，2004，40(5)：546-550.

LEI Zuo-sheng, REN Zhong-ming, YAN Yong-gang, et al. Mold flux channel dynamic pressure in electromagnetic continuous casting[J]. Acta Metallurgica Sinica, 2004, 40(5): 546-550.

[16] 王子亮，郭世宝，王广林，等. 非正弦振动在板坯连铸机上的应用[J]. 钢铁，2005，40(1)：31-34.

WANG Zi-liang, GUO Shi-bao, WANG Guang-lin, et al. Application of non-sinuous oscillation on slab caster[J]. Iron and Steel, 2005, 40(1): 31-34.

[17] 孟祥宁，朱苗勇. 高拉速连铸结晶器非正弦振动波形[J]. 过程工程学报，2006，6(增刊)：91-94.

MENG Xiang-ning, ZHU Miao-yong. Non-sinusoidal oscillation profile for continuous casting mold with high casting speed[J]. The Chinese Journal of Process Engineering, 2006, 6(suppl.): 91-94.

收稿日期：2006-04-17；修订日期：2006-12-21

通讯作者：朱苗勇，教授；电话: 024-83686995；E-mail: myzhu@mail.neu.edu.cn, xn_meng@126.com

(编辑　龙怀中)