
Computer simulation for precipitation process of θ (Ni3V) and γ′ (Ni3Al) with microscopic phase-field method
HOU Hua(侯 华)1, XU Hong(徐 宏)2, ZHAO Yu-hong(赵宇宏)2
1. College of Materials Science and Technology,North University of China, Taiyuan 030051, China;
2. College of Materials Science and Technology,Taiyuan University of Technology, Taiyuan 030024, China
Received 20 April 2006; accepted 30 June 2006
Abstract: With the microscopic phase-field model, the precipitation process of aged alloys was explored by computer simulation, which could clarify some discussional views on the precipitation mechanisms of alloys. The precipitation process of Ni75Al2.5V22.5 alloy was studied. From the simulated atomic pictures, calculated order parameters and volume fraction of different precipitates, it’s found that the θ ordered phase precipitates earlier than γ′ ordered phase by congruent ordering+spinodal decomposition mechanism and thus produces a nonstoicheometric θ single ordered phase. Then, the nonstoicheometric γ′ phase is precipitated by a non-classical nucleation and growth mechanism at the APBS of θ phases. Meanwhile, both of them transform to stoicheometric ordered phases.
Key words: Ni3V; Ni3Al; phase-field model; precipitation process; computer simulation
1 Introduction
The microscopic phase-field model was used for the aged alloy system with high concentration gradient, any prior assumption on the precipitate and mechanism is not necessary, which can describe the atom clustering, ordering, growth and coarsening of precipitates simult- aneously. So the model is of great importance for studying aging process.
Many experimental and theoretical studies have been made to explored the early precipitation mechanism of Ni-Al based alloys [1-6], yet due to the limitations of apparatus employed, this view was still on discussion now. Therefore, in this paper, we researched the early precipitation mechanism systematically of Ni75Al2.5V22.5 alloy using the microscopic phase-field model.
2 Model
The diffusion relaxation of atoms between lattice sites is described by the ?nsager equation [7], which is the microscopic form of Chan-Hilliard equation. For binary substituted alloy, it’s given by:
 (1)
(1)
where the function P(r, t) characterizes a single site occupation probability on the site r at time t, it can describe the morphology of precipitate. L(r-r′) is a constant matrix related to probabilities of elementary diffusion jumps from r to r′. T is the absolute temperature, kB is the Boltzmann’ s constant. c0 is the average composition. F is the total free energy of the system.
For a ternary system, the atomic configurations and the morphologies are described by the single-site occupation probability functions PA(r, t), PB(r, t) and PC(r, t), and which represent the probabilities of finding an A, B and C at a given lattice site r and a given time t. Since PA(r, t)+PB(r, t)+PC(r, t)=1, only two equations are independent at each lattice site. Assuming the independent variables are PA(r, t) and PB(r, t), the microscopic diffusion equations for ternary systems can be written as [8]:
 (2)
(2)
where Lαβ(r-r′) are the exchange probabilities between a pair of atoms α and β at lattice site r and r′ per unit time, αβ=A, B, and C.
In the single-site approximation, the Nonequilibri-
um free energy F for a ternary system is given by[9]
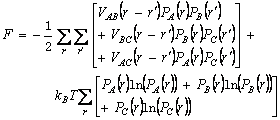 (3)
(3)
and
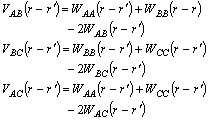 (4)
(4)
where Vαβ(r-r′) and Wαβ(r-r′) are respectively the effective and factual interaction energies between a pair of atoms α and β at lattice site r and r′. Here a fourth-neighbor interaction model was employed.
Substituting Eqn.(3) into Eqn.(2), the differential term in Eqn.(2) could be written as
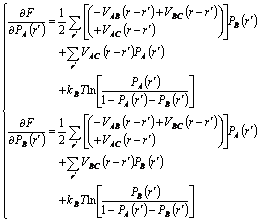 (5)
(5)
Fourier transforming both side of Eqn.(2), and then the precipitation kinetic Eqn.(6), for a ternary alloy system in the reciprocal space, was obtained:
 (6)
(6)
where k is the lattice site vector in the reciprocal space;
 ,
,
VAB(k), VBC(k) and VAC(k) are the Fourier transforms of the corresponding functions. It’s convenient and even computationally advantageous to solve the kinetic equations in the reciprocal space.
The Euler method was used to solve Eqn.(6), and then the inverse Fourier transformation was carried out; finally the relationships between occupation probability and time were obtained [10]. The periodical boundary condition was applied automatically.
3 Results
The atom occupation probability is the solution of phase-field equation, from which the order parameter profiles across any an ordered phase can be obtained, then we can conclude the precipitation mechanism of alloys. The simulated Ni75Al2.5V22.5 alloy is aged at 1 050 K, the simulated atomic pictures at different time are shown in Fig.1, and in which 128×128 grids are calculated.
In Fig.1(a), there is still the disordered Ni matrix supersaturated solid solution, and no composition fluctuation occurs. From Fig.1 (b), we can see some θ(Ni3V) zones with DO22 ordered structures appear, and they are linked by some transitional ordered structures. In Fig.1 (c), nearly single θ phases form and some Al atoms appear at their boundaries. In Fig.1 (d), few γ′ (Ni3Al) phases with L12 ordered structures form mainly

Fig.1 Temporal evolution of occupation probabilities at 1 050 K for CAl=0.025: (a) t=2 ks; (b) t=4 ks; (c) t=6 ks;(d) t=100 ks
at the corners of some connected θ phases and then grow and coarsen further.
According to Fig.1, the θ phase appears as linked zones and γ′ phase form from small nuclei, it seems that we should speculate that the θ phase is precipitated by spinodal decomposition, and the γ′ phase by nucleation and growth mechanism. However, it is not convincing for predicting precipitation mechanism only from the morphology, so the composition order parameters and long-range order parameters of the two kinds of ordered phases (see Figs.2 and 3, respectively) are calculated to explore the precipitation process further.
From Fig.2, it can be seen that the profile curves of both composition and long-range order parameters are almost unchanged, the former is close to the equilibrium value and the latter is close to 1. There is no question that the θ phase is precipitated by a congruent ordering + spinodal decomposition mechanism.
From Fig.3, the γ′ phase appears as small nuclei initially and becomes bigger gradually, and the interface between the two kinds of phases is diffuse. So it can be concluded that the γ′ phase is precipitated by a non-classical nucleation and growth mechanism.
Finally, the volume fraction of the two kinds of ordered phases at different time is calculated, as shown in Fig.4.
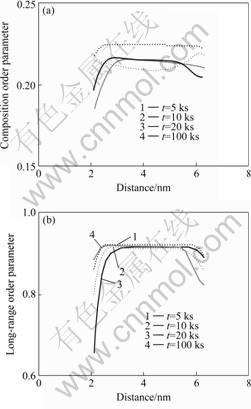
Fig.2 Order parameter profiles across θ phase for CAl=0.025 at different time: (a) Composition order parameter; (b) Long- range order parameter
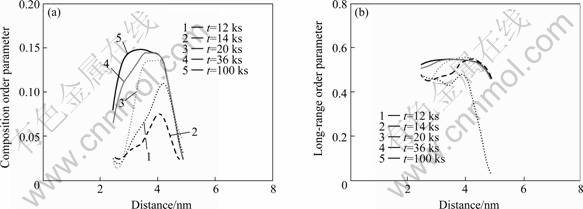
Fig.3 Order parameter profiles across γ′ phase for CAl=0.025 at different time: (a) Composition order parameter; (b) Long-range order parameter
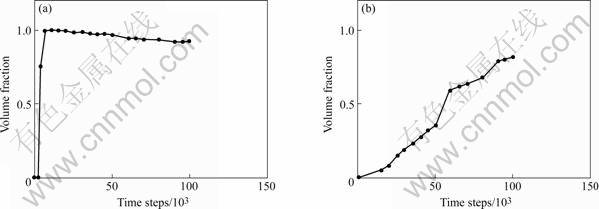
Fig.4 Variation in volume fraction of ordered phases with time for Ni75Al2.5V22.5: (a) θ phases with DO22 structure; (b) γ′ phases with L12 structure
In Fig.4 (a), the volume fraction of θ phase mounts up to the maximum value close to 1 quickly, that’s corresponded to the congruent ordering stage. Then it begins to decline gradually, that’s because the occurrence of spinodal decomposition.
In Fig.4 (b), during the time studied, the volume fraction of γ′ phase increases all the while, because the system hasn’t get it’s equilibrium, still at the nucleation and growth stage.
Therefore, the volume fraction also presents strong support for above discussion of the precipitation mechanism.
So, for Ni75Al2.5V22.5 alloy aged at 1 050 K, the precipitation mechanism can be summarized as shown in Fig.5.
In Fig.5, the nonstochiometric order phase means that the alloy system is still not arrive at the equilibrium state, and the precipitated phases are undergoing the transform process, this can be seen from the color depth of gray map, or the value of order parameters which do not get to its’ equilibrium value.
The authors have simulated the same aged alloy system with different Al compositions [11, 12], it
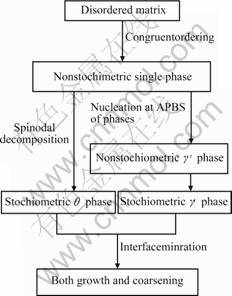
Fig.5 Precipitate process of Ni75Al2.5V22.5 alloy
shows that it is believable and promising to research the precipitation process by employing the microscopic phase-field model.
4 Conclusions
1) The microscopic phase-field model is proved to be a powerful tool for simulating the precipitation process of aged alloys.
2) For Ni75Al2.5V22.5 alloy, θ ordered phase is precipitates earlier than γ′ ordered phase by congruent ordering+spinodal decomposition mechanism and thus produces a nonstoicheometric θ single ordered phase. Then, the nonstoicheometric γ′ phase is precipitated by a non-classical nucleation and growth mechanism at the APBS of θ phases. Meanwhile, both of them transform to stoicheometric ordered phases.
References
[1] WENDT H, HASSEN P. Nucleation and Growth of γ′ Precipitates in Ni-14%Al[J]. Acta Metal, 1993, 31(10): 1649-1659.
[2] BANERJEE D, BANERJEE R, WANG Y. Formation of split patterns of γ′ precipitates in Ni-Al via particle aggregation[J]. Scripta Materialia, 1999, 41(9): 1023-1030.
[3] ARDELL A J, MAHESHWARI A. Coherent equilibrium in alloys containing spherical precipitates[J]. Acta Metall Mater, 1995, 43(5): 1825-1835.
[4] STARON P, KAMPMANN R. Early-stage decomposition kinetics in Ni-Al alloys(Ⅰ): Small and wide-angle neutron scattering investigation on Ni-13% Al and cluster dynamic modeling[J]. Acta Mater, 2000, 48: 701-712.
[5] STARON P, KAMPMANN R. Early-stage decomposition kinetics in Ni-Al alloys(Ⅱ): Cluster dynamic modeling of former experimental results[J]. Acta Mater, 2000, 48: 713-720.
[6] SUSUMA O, NORIKO K, TOSHIYUKI F, MASAHARU K. Simplified energy analysis on the equilibrium shape of coherent γ′ precipitates in matrix with a super spherical shape approximation[J]. Intermetallics, 2002, 10: 343-346.
[7] KHACHATURYAN A G. Theory of Structural Transformations in Solids[M]. New York: Wiley, 1983. 139.
[8] CHEN L Q, KHACHATURYAN, A G. Computer simulation of decomposition reactions accompanied by a congruent ordering of the second kind[J]. Scripta Metallurgica et Materialia, 1991, 25: 61-66.
[9] CHEN L Q. Computer simulation of spinodal decomposition in ternary systems[J]. Acta Metall Mater, 1994, 42(10): 3503-3513.
[10] CHEN L Q, KHACHATURYAN A G. Computer simulation of structural transformations during precipitation of an ordered intermetallic phase[J]. Acta Metall Mater, 1991, 39(11): 2533-2551.
[11] ZHAO Y H, HOU H, XU H, et al. Atomic- scale computer simulation for early precipitation process of Ni75Al9V16 alloy[J]. Journal of Material Science and Technology, 2003, 19(S1): 17-19.
[12] ZHAO Y H, CHEN Z, WANG Y X, et al. Atomic-scale computer simulation for early precipitation process of Ni75Al10V15 alloy[J]. Progress in Natural Science, 2004, 14(3): 241-246.
(Edited by HE Xue-feng)
Corresponding author: HUA Hua; Tel: +86-351-3921264; Fax: +86-351-3924442; E-mail: houhua@263.net