基于模糊网络分析法的维修策略决策
彭安华1, 2，肖兴明2，岳睿2
(1. 淮海工学院 工程训练中心，江苏 连云港，222005；
2. 中国矿业大学 机电工程学院，江苏 徐州，221116)
摘要：维修策略决策过程中考虑的因素众多，并且各因素之间存在不同程度的相互关联，因此是一个典型的关联多属性决策问题。网络分析法作为层次分析法的推广，是处理关联多属性决策问题一种常用的方法。为描述决策过程中的模糊性和不确定性，利用三角模糊数构造判断矩阵。然后采用对数最小二乘法求出模糊权重，利用面积重心法将模糊数转化为精确数。以热电厂发电设备维修方案决策为例，阐明该决策过程，最终从3种常见的备选方案中选出计划维修方案为该企业当前应执行的方案。最后将网络分析法得出的结论与层次分析法得出的结论对比，进一步说明网络分析和的可行性和优越性。
关键词：维修策略；模糊网络分析；对数最小二乘法；超矩阵；面积重心法
中图分类号：TH133.33；TD421 文献标志码：A 文章编号：1672-7207(2014)03-0783-07
Maintenance strategy decision making using fuzzy analytic network process (FANP)
PENG Anhua1, 2, XIAO Xingming2, YUE Rui2
(1. Engineering Training Center, Huaihai Institute of Technology, Lianyungang 222005, China;
2. School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, China)
Abstract: Since decision making for maintenance strategy needs to simultaneously take into account too many attributes which, more often than not, depend on each other, the decision making of maintenance strategies belongs to classical multi-attribute one in the presence of relationships (RMADM). FANP (Fuzzy Analytic Network Process) as the generalization of FAHP ((Fuzzy Analytic Hierarchical Process) is a widely used method to deal with RMADM. Fuzzy weights are derived by using the logarithmic least square method (LLSM) from fuzzy judgment matrices in which the compared values between any two criteria are expressed in triangular fuzzy numbers (TFN), so as to capture fuzziness and uncertainness of the judgments of decision makers, and then are translated into exact numbers using the method of centre of area (COA). Taking maintenance strategy decision making for power generation equipments in a thermal power plant for example, the procedure is detailed and the scheduled maintenance strategy is selected as the best maintenance strategy among the three alternatives: corrective, scheduled, and condition-based maintenance. Finally, the feasibility and advantages of FANP are further illustrated through the conclusion comparison between using FAHP and FANP.
Key words: maintenance strategy; fuzzy analytic network process (FANP); logarithmic least square method (LLSM); super matrices; centre of area (COA)
维修工作对于保证生产设备的可靠性和可用度、保证设备的安全水平具有重要作用，然而一直以来没有像项目管理和产品质量一样受到研究人员的重视[1]。Al-Najjar等[2]指出，维修不当和维修过剩将造成维修费用浪费。目前，关于维修的研究成果逐渐增多，维修的角色也从“必要但讨厌的工作”转变为“利润发动机”，甚至是“企业获得世界竞争力的伙伴”。在设备维修工作中主要有故障后维修(corrective maintenance, CM)、计划维修(scheduled maintenance, SM)、视情维修(condition-based maintenance, CBM) 3种维修策略。故障后维修的特点是“不坏不修，坏了再修”，最大优点是充分利用了零部件的使用寿命，但缺乏灵活性和主动性，浪费了较多的剩余修理，当停机损失较小，只需调整或更换易损件即可排除故障时，或者对随机故障(无法事前预知或避免的故障)采用故障后维修比较经济。计划维修也称周期性预防维修，当对产品失效的物理规律具有准确或较准确把握条件下，为降低设备的故障发生率和零部件的功能衰退、性能劣化，根据预先确定的时间间隔或指定的标准执行维修，其优点是降低了功能性故障发生率、减少了停机时间，便于设备计划管理，有利于保持产品的可靠性水平，但计划维修很难解决修理时间的固定性与设备使用状况随机性之间的矛盾，从而不可避免地会造成维修过剩或维修不足。视情维修也称为状态监测维修，是应用监测手段在对产品“健康”状态实时把握情况下，从避免故障或事故角度所采取的维修活动，是提高产品安全性的关键。其优点是维修的针对性强，能够充分利用零部件的工作寿命，又能有效排除故障，使停机损失降到最低，大大提高了维修的有效性、经济性和及时性。但开展状态维修工作，企业需要安装在线检测设备，组建状态监测中心，配备相应数量的专业技术人员，配齐必要的监测仪器、仪表、设备等，而且有的故障模式比较难以监测定位，致使有的数据不稳定或不真实，以致本来有可能及时发现的缺陷却未能及时检测出。3种维修策略各有其优缺点、各有其适用范围决不能相互替代。夏良华等[3]指出：关键设备优先考虑状态维修，主要设备优先考虑计划维修，次要设备优先考虑故障后维修，但有些设备尽管关键，由于其故障模式特征的识别在技术上存在困难，也不宜采用状态维修。合理维修策略应该在考虑多种因素的基础上综合决策，例如故障可能产生的危害、各种维修方式产生的费用、附加效益和技术可行性等，使得最少的维修资源消耗取得最佳的维修效果。关于维修策略决策在国内外吸引了很多学者的注意。李常有等[4-5]分别提出了在权重已知和未知情况下基于ELECTRE(消去与选择法)的混合数据决策法。Bashiri等[6]提出了运用交互式线性分配法的决策方法。Bertolini等[7-9]提出了运用层次分析(AHP)的决策方法。AHP能帮助决策人员将问题的几个重要方面构建类似于系谱树的层次结构，通过两两比较得到判断矩阵，从而对准则和备选方案评分。但现有的大部分关于维修决策方面的文献都存在一个主要问题，即认为各属性之间相互独立，从而影响了决策的可靠性。而实际上维修决策考虑的各因素之间往往是相互影响和制约，一般来讲，故障危害大的维修费用相应也高些，技术可靠性好的维修方案则员工易于接受。所以维修方案的决策是因素之间关联的多属性决策。基于关联的决策方法主要有2种：一种是采用模糊积分的方法，另一种是网络分析(ANP)法[10]。采用模糊积分方法存在模糊测度难以确定的问题，采用λ模糊测度的方法虽然可以降低确定模糊测度的难度，但确定出的模糊测度只能表示各因素之间的一类交互作用，即要么全部存在正的交互作用，要么全部存在负的交互作用，减弱了模糊测度的表达能力。ANP是基于AHP并考虑到因素之间的相互关联而提出了一种多因素综合评价方法。由于该方法考虑到了属性之间的关联，因此能够比较逼真地刻画了客观事物的复杂性，近年来在合作伙伴决策[11]、风险评估[12]等方面得到广泛的应用。但这些文献在由判断矩阵求权重时都是采用特征根的方法确定权重，即由最大特征根对应的特征向量作为权重向量，实际上当判断矩阵的阶数较高时，往往很难达到一致性的要求。本文作者采用对数最小二乘法由模糊判断矩阵得出模糊权重，再由面积重心法将模糊权重转化为精确权重，并将该方法运用于发电设备维修方案决策。
1 模糊网络分析法
AHP方法首先建立如图1所示的递阶层次结构，目标层决定准则层，准则层决定子准则层，子准则层决定方案层，各层之间不存在反馈，各层内部元素之间是相互独立的。ANP方法首先建立如图2所示的网络结构图，在网络结构图中准则层、方案层都视为元素组，各子准则、各方案都视为元素，各元素组之间、各元素组内部各元素之间都相互影响与制约。模糊网络分析法的步骤如下：
1.1 构建未加权超矩阵
假设网络结构中有n个元素组E1, E2, …, Ei, …, En，任一元素组Ei中含有ni个元素，分别表示为ei1, ei2, …, eini。现以元素ejl作为比较准则，在元素组Ei中找出由ejl影响或制约的元素，然后将这些元素两两比较，构造模糊判断矩阵，由模糊判断矩阵求出权重列向量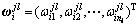
，注意权重列向量中不受ejl影响或制约的元素对应在权重向量的权重直接赋为0，由于l=1, 2, …, nj则由nj个列向量组成矩阵
。
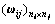(1)
矩阵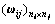中每一列表达了以元素组Ej中的任一元素ejl (l=1, 2, …, nj)为比较准则，元素组Ei中元素之间的权重列向量。由于j=1, 2, …, n，i=1, 2, …, n则以矩阵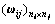为块，则组成了未加权的超矩阵
…
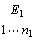
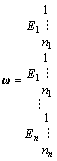
(2)
图1 AHP递阶层次结构
Fig. 1 Hierarchy structure
图2 ANP中的网络结构
Fig. 2 Nonlinear network structure
1.2 构建加权超矩阵
以元素组Ej为比较准则，在元素组Ei(i=1, 2, …, n)中找出由Ej影响或制约的元素组，将这些元素组两两比较构造模糊判断矩阵，再由模糊判断矩阵求出权重向量
,注意权重列向量中不受Ej影响或制约的元素组对应在权重向量的权重值直接赋为零。分别将(j=1, 2, …, n)与未加权超矩阵按下式的方式相乘构成加权超矩阵
，加权超矩阵是列随即矩阵，即每列的和为1。
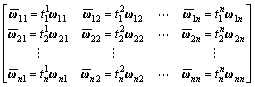(3)
1.3 求极限超矩阵
加权超矩阵体现的只是直接优势度，而不能体现间接优势度。例如元素A影响元素B，而元素B又影响元素C，B相对于A的优势度、C相对于B的优势度就是直接优势度，既然元素A影响元素B，而元素B又影响元素C，元素A影响元素肯定也影响元素C，则C相对于A的优势度就是间接优势度，而加权超矩阵无法直接体现。对加权超矩阵求平方
，则体现了第二步间接优势度。为了求出稳定的权重，从加权超矩阵出发，依次求二次方，即
当第1次出现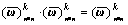
，
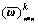就是稳定的权重，即极限超矩阵。每自乘必须进行列归一化处理，以保证加权超矩阵是列随机矩阵。文献[13]已证明极限超矩阵的每一列都相同，即是相对于任意元素的极限相对优势度，即权重。
1.4 求模糊权重
设
是模糊互反判断矩阵
的排序向量，其中
，
表示三角模糊数的下界，
表示中值(并不一定为下界和上界的均值)，
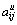表示上界，满足
,
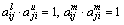。如果模糊互反判断矩阵是完全一致性的，则
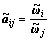(4)
由于决策者在实际决策时所给出的模糊互反判断矩阵往往是不同程度具有非一致性，所以上式一般不成立，为此引入偏差项
(5)
合理的权重向量应该是下列目标函数的最优解
(6)
这种方法称为对数最小二乘法(LLSM)，根据文献[14]，可得权重
，
， 
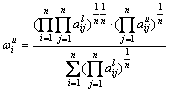(7)
1.5 模糊权重精确化
模糊数的排序不仅要考虑“均值”，还要考虑模糊数的散布程度，采用面积重心法(COA, Center of Area)将三角模糊数转化为一个精确数。面积重心法就是求出模糊数隶属函数曲线和横坐标包围区域面积的重心，选这个重心对应的横坐标值，作为三角模糊数的精确数的精确值。该方法直观合理、言之有据，但计算过程略显繁杂。设一个三角模糊数
，隶属度函数图如图3所示，其隶属函数表示如下：
图3 三角模糊数的隶属度函数
Fig. 3 Membership function for triangular fuzzy number
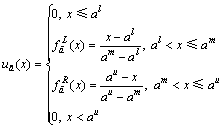(8)
式中：
：
；
：
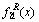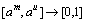，则三角模糊数
的重心横坐标，也即精确值a为
(9)
2 发电设备维修方式决策
杭联热电设备是一个小型热电厂。为了保证用户供电的连续性，设备的突发性故障概率应可能降低，当前主要采取“定期强制保养，计划预防维修”的维修理念，维修效果不是很理想，但开展状态维修工作需要初始费用投入很高，又担心投入产出比不合算。因此，试图针对不同设备或部件选择最恰当的维修方式，而不是为所有设备都选用最先进的维护方式。本应用实例主要是对热电厂的发电设备选择恰当的维修方式。该实例来自文献[15]，在该文献中采用模糊层次分析法决策，最终决定采用状态维修策略，但该方法没有考虑到因素之间的关联，因此结果受到质疑。本文拟采取网络分析法进一步考虑该问题。
2.1 确定元素组及元素之间的关联
确定元素组及元素之间的关联主要有经验法与定性和定量相结合的方法，解释结构模型ISM (Interpretive Structural Modeling)是主要的定性和定量相结合的方法[16]，本文采用ISM和通过征询热电厂相关专家的意见，建立如图4所示的网络结构。除了方案组内各元素之间相对独立之外，其他元素组内的元素之间都存在不同程度的关联。2个元素组之间只要有1对元素之间关联，则这2个元素组之间关联。
2.2 求出未加权超矩阵
一个元素(元素组)i与另一个元素(元素组) j的相对于准则的重要度大致差不多，则
；一个元素(元素组)i相对于准则的重要度大约是另一个元素(元素组)j的x倍，则
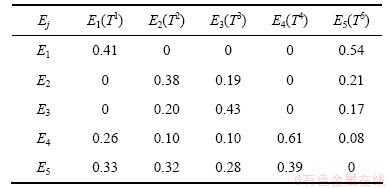
；一个元素(元素组)i相对于准则的重要度大约是另一个元素(元素组)j的y倍到z倍之间，则
。根据这些办法再根据判断矩阵的互反性，依次针对网络结构图中的每一个元素ejl(j=1, 2, …, 5; l=1, 2, …, nj)构造模糊互反判断矩阵。例如相对元素人员e11，需要构造3个模糊判断矩阵：在元素组安全性E1中元素环境e12和设备e13之间两两比较构造一个2阶模糊判断矩阵，在元素组可行性E4中员工接受性e41和技术可靠性e42之间两两比较构造一个2阶模糊判断矩阵，在方案组E5中3个方案之间两两比较构造一个3阶模糊判断矩阵。这样总共需要构造40个模糊判断矩阵，然后依次按式(7)和(9)求出模糊判断矩阵导出的精确权重向量。限于篇幅，本文直接把得到的精确权重值列于表1中，即未加权超矩阵。
图4 维修策略决策网络结构图
Fig. 4 Network structure for decision making on maintenance strategies
2.3 求加权超矩阵
分别以元素组Ej(j=1, 2, 3, 4, 5)作为比较准则，其他元素组相对于Ej(j=1, 2, 3, 4, 5)的重要性两两比较构造模糊互反判断矩阵，注意如果一个元素组内元素之间存在关联，则相对于该元素组构造模糊互反判断矩阵时，该元素组自身也是一个两两比较对象；反之，如果一个元素组内元素之间不存在关联，则相对于该元素组构造模糊互反判断矩阵时，两两比较对象不包括该元素组自身。例如以元素组E2为比较准则，则元素组E2，E3，E4和E5两两比较构造一个4阶互反模糊判断矩阵；以元素组E5为比较准则，则元素组E1，E2，E3和E4两两比较构造的是一个4阶模糊判断矩阵。相对于元素组为准则，元素组之间两两比较需要构造5个模糊判断矩阵。现以元素组E5为比较准则，构造的4阶模糊判断矩阵为例阐明如何确定精确权重的步骤。
(1) 构造模糊互反判断矩阵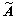
。
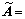
(2) 求出模糊权重。根据式(7)分别求出三角模糊权重如下
，
，
，
。
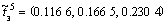(3) 求精确权重并归一化。利用式(9)将三角模糊数转化为精确数并保留2位有效数字可得，
，
，
，
，因为方案组E5自身元素之间不存在关联，即方案组不影响方案组，所以在在权重列向量
中
直接赋值为0。所以权重列向量为
。同理可求得相对于E1，E2，E3和E4构造模糊判断矩阵的权重T1，T2，T3和T4列于表2中，与比较准则无关的元素组在对应权重列向量的对应位置直接赋0。最后按矩阵(3)的方式将元素组权重列向量分别乘以超矩阵对应的列矩阵块，即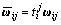
，构造加权超矩阵。
2.4 求极限超矩阵
经过3次自相乘，即
矩阵的每一列都相同，所以就是极限超矩阵，它的每一列都为
(0.077 4, 0.077 9, 0.108 8, 0.026 3, 0.024 3, 0.039 2, 0.015 4, 0.038 9, 0.019 6, 0.160 9, 0.153 5, 0.088 8, 0.109 7, 0.059 9)T，即为相对于任一元素的稳定权重。可知方案组3种方案之间的相对权重为 (0.088 8, 0.109 7, 0.059 9)，经过归一化处理可知3种维修方案的合成排序结果为：
，
，
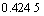。可见热电厂的发电设备选择仍应该选择计划维修方案。
表1 未加权超矩阵
Table 1 Un-weighted super-matrix
表2 元素组权矩阵
Table 2 Weight matrix for element clusters
2.5 结果讨论
网络分析法是层次分析法的推广，如果网络分析中不考虑元素及元素组之间的关联，则网络分析法退化为层次分析法，网络分析法中的自乘是为了从直接关联中找到元素之间的间接关联，而层次分析法中根本就不考虑元素之间的关联。根据文献[15]的结果，可见如果不考虑属性之间的关联，则应该采取视情维修策略。显然是本文决策更为合理，因为考虑属性之间的关联，更加符合现实情况。故障维修主要在节省费用和节省人员培训方面具有明显的优势，其他方面处于明显劣势；计划维修在员工接受性、技术可靠性和减少备件库存方面具有明显的优势，费用和人员培训方面的投入也不算多；视情维修有助于人员安全、故障识别和减少生产损失，但是却提高了费用而且技术可行性也较差，而且费用和可行性之间不仅相互影响而且影响到其他因素，极大地降低了视情维修策略的得分，采用层次分析却无法考虑这种影响。当然维修策略是动态的[17]，随着企业生产技术的进步，状态监测稳定性和可靠性的提高、费用的逐步降低，员工的素质逐渐提高，该企业可以逐步由当前的“定期强制保养、计划预防维修”的维修理念逐步过渡到视情维修的维修理念，以提高设备的安全性和减少生产损失。文献[18]介绍了“Super Decisions”超级决策软件，可以使得ANP决策过程简单化，但目前该决策软件只能处理由精确数构成的判断矩阵，无法处理模糊判断矩阵情况。实际上在Matlab软件中通过编程的方法计算也可使计算过程大为简化。
3 结论
(1) 网络分析法由于考虑了属性之间的关联，因此决策结果比传统的层次分析更为可靠。
(2) 采用网络分析需要建立判断矩阵的数量比层次分析法要多得多，本文总共建立了45个判断矩阵，而采用层次分析法则总共只需建立16个判断矩阵，因此提高了决策的复杂性。
(3) 决策结果的可靠性不仅取决于决策方法，而且还取决于因素选取的合理性和全面性，判断矩阵的构造准确性即判断的准确性。只有专家在全面分析调查的情况下，才能提高决策结果的可行性。
参考文献：
[1] Al-Najjar B, Aisyouf I. Selecting the most efficient maintenance approach using fuzzy multiple criteria decision making[J]. Int J Production Economics, 2003, 84(1): 85-100.
[2] Al-Najjar B. Total quality maintenance: An approach for continuous reduction in costs of quality products[J]. Int J Quality in Maintenance Engineering, 1996, 2(3): 4-20.
[3] 夏良华, 贾希胜, 徐英. 设备维修策略的合理选择与决策流程[J]. 火炮发射与控制学报, 2006(4): 63-67.
XIA Lianghua, JIA Xisheng, XU Ying. Procedures for decision making in equipment maintenance strategies[J]. Journal of Gun Launch and Control, 2006(4): 63-67.
[4] 李常有, 徐敏强, 郭耸, 等. 具有混合数据的维修策略决策方法[J]. 机械工程学报, 2008, 44 (10): 32-37.
LI Changyou, XU Minqiang, GUO Song, et al. Approach for maintenance strategy decision making with mixed data[J]. Chinese Journal of Mechanical Engineering, 2008, 44(10): 32-37.
[5] 李常有, 徐敏强, 郭耸, 等. 混合数据集未知权值下的维修策略决策方法[J]. 航空动力学报, 2008, 23(9): 1628-1632.
LI Changyou, XU Minqiang, GUO Song, et al. Decision making method for maintenance strategy with mixed data and unknown priority vector[J]. Journal of Aerospace Power, 2008, 23(9): 1628-1632.
[6] Bashiri M, Badri H, Hejazi T H. Selecting optimum maintenance strategy by fuzzy interactive linear assignment method[J]. Applied Mathematical Modeling, 2011, 35(1): 152-164.
[7] Bertolini M, Bevilacqua M. A combined goal programming -AHP approach to maintenance selection problem[J]. Reliability Engineering and System Safety, 2006, 91: 839-848.
[8] Bevilacqua M, Braglia M. The analytic hierarchy process applied to maintenance strategy selection[J]. Reliability Engineering & System Safety, 2000, 70: 71-83.
[9] 顾煜炯, 陈昆亮, 杨昆. 基于熵权和层次分析法的电站设备维修方式决策[J]. 华北电力大学学报, 2008, 35(6): 72-76.
GU Yujiong, CHEN Kunliang, YANG Kun. Maintenance mode decision making for power plant equipment based on entropy and analytic hierarchy process[J]. Journal of North China Electric Power University, 2008, 35(6): 72-76.
[10] 章玲, 周德群. 基于关联的多属性决策分析理论研究综述[J]. 管理评论, 2008, 20(5): 51-57.
ZHANG Lin, ZHOU Dequn. A review on theory research into multi-attribute decision making in the presence of relationships[J]. Management Review, 2008, 20(5): 51-57.
[11] Razmi J, Rafiei H, Hashemi M. Designing a decision support system to evaluate and select suppliers using fuzzy analytic network process[J]. Computer & Industrial Engineering, 2009, 57: 1282-1290.
[12] 张悍东, 严钟. 动态联盟风险评估的网络分析法及其应用[J]. 计算机集成制造系统, 2008, 14(1): 197-202.
ZHANG Handong, YAN Zhong. Risk evaluation in dynamic alliance and its application using analytic network process[J]. Computer Integrated Manufacturing Systems, 2008, 14(1): 197-202.
[13] 王莲芬. 网络分析法的理论与算法[J]. 系统工程理论与实践, 2001(3): 44-50.
WANG Lianfen. The theory and algorithm of analytic network process[J]. Systems Engineering-Theory and Practice, 2001(3): 44-50.
[14] 高会生, 冉静学, 孙逸群. 基于改进的FAHP电力通信网风险评估[J]. 系统工程理论与实践, 2008(3): 133-138.
GAO Huisheng, RAN Jingxue, SUN Yiqun. Risk evaluation of communication network of electric power based on improved FAHP[J]. Systems Engineering-Theory and Practice, 2008(3): 133-138.
[15] 彭安华, 王智明. 基于模糊层次分析法的维修方式群体决策模型[J]. 机械强度, 2012, 34(3): 403-409.
PENG Anhua, WANG Zhiming. Group decision making for maintenance strategies based on fuzzy analytic hierarchy process[J]. Journal of Mechanical Strength, 2012, 34(3): 403-409.
[16] Yang J L, Chiu H N, Tzeng G H, et al. Vendor selection by integrated fuzzy MCDM techniques with independent and interdependent relationships[J]. Information Science, 2008, 178(21): 4166-4183.
[17] Waeyenbergh G, Pintelon L. A framework for maintenance concept development[J]. International Journal of Production Economics, 2002, 77(3): 299-313.
[18] 孙宏才, 田平, 王莲芬. 网络层次分析法与决策科学[M]. 北京: 国防工业出版社, 2011, 1.
SUN Hongcai, TIAN Ping, WANG Lianfen. Analytic network process and decision making science[M]. Beijing: National Defense Industry Press, 2011, 1.
(编辑 陈爱华)
收稿日期：2013-03-04；修回日期：2013-05-18
基金项目：江苏省“六大人才高峰”项目(2011-ZBZZ-046)；江苏省高校科研成果产业化项目(JH10-58)
通信作者：肖兴明(1962-)，男，四川广汉人，教授，博士，从事矿山机械状态监测与故障诊断的研究；电话：13952299638；E-mail: xl6265@cumt.edu.cn
