DOI: 10.11817/j.issn.1672-7207.2017.07.024
水泥改良泥质板岩土动力特性试验
陈乐求1, 2,陈俊桦1,张家生1,陈积光2
(1. 中南大学 土木工程学院,湖南 长沙,410075;
2. 湖南理工学院 土木建筑工程学院,湖南 岳阳,414006)
摘要:针对未改良和水泥改良的泥质板岩砂土,利用振动三轴仪开展不同加载频率和围压作用下的循环振动加载试验,研究土的动弹性模量、阻尼比、动力强度和动力累积变形等参数的变化规律,对比改良土和未改良土的试验结果,分析和评价改良效果。研究结果表明:改良土的动应力与动应变关系骨干曲线为双曲线;改良土阻尼比随动应变幅值增大而增大,近似为双曲线函数关系;改良土初始动弹性模量随围压增大而增大,最大阻尼比随围压增大而减小;改良土初始动弹性模量随加载频率增大而增大,但加载频率对最大阻尼比的影响不大;改良土动应力强度和破坏振次的对数呈线性递减关系;水泥改良后,泥质板岩土的动力强度和初始动弹性模量显著提高,而最大阻尼比变化不大。改良土动力变形稳定性比未改良土的强。
关键词:土动力学;动三轴试验;动弹性模量;阻尼比;动应力强度;动力累积变形
中图分类号:TU41 文献标志码:A 文章编号:1672-7207(2017)07-1858-08
Test of dynamic properties of argillite-slate soil improved by cement
CHEN Leqiu1, 2, CHEN Junhua1, ZHANG Jiasheng1, CHEN Jiguang2
(1. School of Civil Engineering, Central South University, Changsha 410075, China;
2. Department of Construction & Engineering, Hunan Institute of Science and Technology, Yueyang 414006, China)
Abstract: Test of dynamic properties of argillite-slate soil and the soil improved by cement were carried out using dynamic triaxial compressive equipment under different conditions of loading frequency and confining pressure. The changes of dynamic elastic modulus, damping ratio, dynamic strength and cumulative strain were obtained by the test. The improvement effects were analyzed and evaluated by comparing the dynamic properties of the improved soil with that of the one unimproved. The results show that the stress-strain backbone curve of improved soil can be fitted with hyperbolar. The damping ratio increases with the increase of the amplitude of dynamic strain, and their relationship can also be fitted with hyperbolic curve. The initial value of dynamic elastic modulus increases with the increase of the confining pressure, while the maximum value of damping ratio has the opposite trend. The initial value of dynamic elastic modulus increases with the increase of the loading frequency, while there are little influences of loading frequency on the maximum damping ratio. The dynamic stress strength decreases linearly with the logarithm of cycle times. After the improvement, both the dynamic strength and the initial dynamic elastic modulus are enhanced significantly while the maximum damping ratio changes little. The dynamic deformation of the improved soil is more stable than that of the one unimproved.
Key words: soil dynamics; dynamic triaxial test; dynamic elastic modulus; damping ratio; dynamic stress strength; dynamic cumulative deformation
当土石料不能满足路基填筑要求时,需要对其进行物理改良或者化学改良。物理改良一般通过改变级配的方式改变土石料的强度和刚度等物理力学参数。对于物理改良效果不好的土料,如黄土、盐渍土等受水环境影响较大的不良土料,需要采用化学方法进行改良。化学改良通常是在不良填料中掺入石灰或者水泥等,利用化学反应加强土内部联结结构联系,从而增强土的力学稳定性和水稳性等。从内部结构看,化学改良土比物理改良土、普通土等要复杂。由于路面上车辆荷载作用是引起路基变形与破坏的主要原因,因此,化学改良土的动力性质是路基工程领域的研究热点之一[1-12]。例如,徐望国等[1]研究了水泥土动强度和变形特性等,李池龙[2]研究了石灰改良土的动弹性模量与阻尼比的特性。研究路基土动力性质的试验通常包括现场试验和室内试验。现场试验通常为现场波速试验,通过现场测试振动波的传播速度,以该物理参数反映路基填土的动力特性。室内试验通常包括共振柱试验[13]、离心机动力试验[14]、直剪试验[15-16]和振动三轴试验等[8-11]。目前,振动三轴试验是最为常用的研究方法。通常利用振动三轴试验研究土的动强度、动弹性模量、阻尼比和累积变形等力学参数的变化规律,得到土的动力特性。如贺建清等[8]利用振动三轴仪研究了石灰土填料的动弹性模量和阻尼比特性,毛成等[11]利用振动三轴仪研究了改良膨胀土的动强度和动力累积变形特性。泥质板岩遇水易软化、崩解,水稳性差,是一种较常见的软岩。泥质板岩破碎后形成的土料保留了母岩的物理化学性质,是需要化学改良的不良填料。泥质板岩在我国分布较广,不少公路和铁路路基的建设项目经过泥质板岩区域,因此,针对泥质板岩改良土动力性质的研究具有重要的工程意义。为此,本文作者利用振动三轴试验研究水泥改良后的泥质板岩土的动强度、动弹性模量、阻尼比和累积变形等,研究水泥改良泥质板岩土的动力特性。通过对比改良土样和未改良土样的试验结果,评价水泥改良效果,以期为泥质板岩改良土的工程应用提供参考。
1 泥质板岩改良土振动三轴试验方案
1.1 试验材料及制样
试验所取土样来自湖南岳阳市区。土样为褐黄色泥质板岩土。土中白云母与绿泥石等亲水矿物成分的质量分数较高,土遇水易软化,崩解,水稳性差。土样的天然含水率为5%~13%,密度为1.04~1.70 g/cm3。
试验设备为DDS-70微机控制电磁式振动三轴试验系统。试样为圆柱体,其直径为39.5 mm,高为80.0 mm。对于未改良试样,试样的压实度为96%,含水率为11%,干密度为2.20 g/cm3。试样的颗粒粒径小于2 mm,其中,细粒土质量分数约为10.4%。不均匀系数为5.2,曲率系数为1.1。土样的级配曲线见图1。根据GB/T 50145—2007“土的工程分类标准”,未改良试样为级配良好的含细粒土砂。改良试样的加固剂为普通硅酸盐P.O32.5。在一般情况下,当土中水泥质量分数≥4%时,改良土的强度和水稳性均可满足路基设计要求[17-18]。因此,从工程应用角度出发,本文试验在由图1所示级配曲线确定的未改良土中掺入质量分数为5%的水泥,以96%的压实度、11%的含水率和2.20 g/cm3的干密度制作改良试样。

图1 泥质板岩土的级配曲线
Fig. 1 Gradation curve of argillite-slate soil
1.2 试验设计
试验为循环振动加载试验,包括动弹性模量与阻尼比试验、动强度试验和动力累积变形试验。试样包括改良土样和未改良土样。
考虑到当标准养护龄期达到28 d后,水泥的强度逐渐步入稳定阶段,对试样进行标准养护。当养护龄期达到28 d时,对改良土样进行试验。
影响土的力学性质的因素很多,包括孔隙比、含水率、围压、加载动应力幅和加载频率等,其中,围压、加载动应力幅值以及加载频率是试验和工程中最常用的参数。本文主要的试验控制参数为围压、动应力幅值和加载频率。主要的试验条件及方法说明如下。
1) 动弹性模量与阻尼比试验等循环动力加载试验施加的振动荷载形式相同,如图2所示。振动荷载施加在试样轴向,为等幅值正弦波荷载,其表达式为
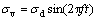 (1)
(1)
式中: 为轴向动应力;
为轴向动应力; 为动应力幅值;f为加载频率;t为作用时间。
为动应力幅值;f为加载频率;t为作用时间。
2) 对于动弹性模量与阻尼比试验,围压 分别为100,150和200 kPa,频率f为1,2和4 Hz。先采用等向固结方式施加静荷载,然后在不排水条件下,轴向逐级施加图2所示荷载。每一级为1个循环,循环次数N=5~10。各级动应力幅值计算为
分别为100,150和200 kPa,频率f为1,2和4 Hz。先采用等向固结方式施加静荷载,然后在不排水条件下,轴向逐级施加图2所示荷载。每一级为1个循环,循环次数N=5~10。各级动应力幅值计算为
 (2)
(2)
式中:k为动静应力比,k=0.1~0.8。对于动弹性模量与阻尼比试验,每一级循环对应1个k。

图2 动力荷载时程曲线
Fig. 2 Time-history curve of dynamic load
根据试验结果测定动弹性模量Ed和阻尼比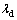 以及它们随应变幅值的变化规律。阻尼比
以及它们随应变幅值的变化规律。阻尼比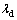 的具体计算过程和计算表达式见文献[9]。动应力—动应变骨干曲线关系式为
的具体计算过程和计算表达式见文献[9]。动应力—动应变骨干曲线关系式为
 (3)
(3)
式中: 为任意1个振次内的正弦波动应力幅值;
为任意1个振次内的正弦波动应力幅值; 为相应振次内的动应变幅值。
为相应振次内的动应变幅值。
3) 对于动强度试验,围压 分别为100,150和200 kPa。频率f为1Hz。先采用等向固结方式施加静荷载,然后在不排水条件下从轴向施加循环振动荷载。
分别为100,150和200 kPa。频率f为1Hz。先采用等向固结方式施加静荷载,然后在不排水条件下从轴向施加循环振动荷载。
动强度试验的破坏标准为:土中孔隙水压力等于围压。破坏时对应的应力为破坏强度 ,即
,即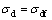 。相应的振次N为破坏振次Nf,即N=Nf。
。相应的振次N为破坏振次Nf,即N=Nf。
4) 对于动力累积变形试验,围压 为100 kPa,频率f为1 Hz。动应力幅值由式(2)确定。不同k对应不同的累积变形曲线。循环作用最大次数为2 000次, 在试验过程中不排水。
为100 kPa,频率f为1 Hz。动应力幅值由式(2)确定。不同k对应不同的累积变形曲线。循环作用最大次数为2 000次, 在试验过程中不排水。
2 试验结果及分析
2.1 动弹性模量试验结果及分析
2.1.1 应力-应变关系骨干曲线与动弹性模量
图3和图4所示为频率f=1 Hz时、不同围压下的应力应变骨干曲线和动弹性模量 与应变幅值
与应变幅值 的关系曲线。从图3可看出:改良土和未改良土的应力应变骨干曲线均近似为双曲线。从图4可以看出:改良土的动弹性模量随动应变幅值增大而减小,但这种减小程度随动应变幅值的增大而逐渐减小。这些结果与通常的非改良土(砂土、黏性土等)振动三轴试验揭示的规律一致[19]。本文试验中泥质板岩改良土的骨干曲线关系
的关系曲线。从图3可看出:改良土和未改良土的应力应变骨干曲线均近似为双曲线。从图4可以看出:改良土的动弹性模量随动应变幅值增大而减小,但这种减小程度随动应变幅值的增大而逐渐减小。这些结果与通常的非改良土(砂土、黏性土等)振动三轴试验揭示的规律一致[19]。本文试验中泥质板岩改良土的骨干曲线关系 -
- 、动弹性模量
、动弹性模量 和应变幅值
和应变幅值 之间的关系
之间的关系 -
- 可用如下的拟合关系式表示[19]:
可用如下的拟合关系式表示[19]:
 (4)
(4)
其中:
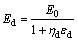 (5)
(5)
 (6)
(6)
 为初始动弹性模量;
为初始动弹性模量; ,
, 和
和 均为拟合参数;
均为拟合参数; 为参考压力,近似取
为参考压力,近似取 kPa。
kPa。
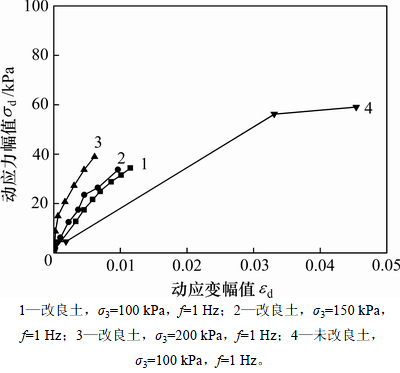
图3 土的骨干曲线
Fig. 3 Backbone curves of soil

图4 动弹性模量与动应变幅值的关系
Fig. 4 Relationship between the dynamic elastic modulus and amplitude of dynamic strain
由试验结果和式(4)~(6)拟合得到参数 ,
, ,
, 和
和 ,拟合结果见表1和表2。
,拟合结果见表1和表2。
表1 参数E0和ηd
Table 1 Parameters of E0 and ηd

表2 不同频率时的参数nE和mE
Table 2 Parameters of nE and mE at different frequencies

典型的改良土动弹性模量和动应变幅值之间的拟合关系曲线见图5。拟合关系式如下:
 (7)
(7)
拟合关系式的相关系数为0.94。

图5 动弹性模量与动应变幅值关系的拟合曲线
Fig. 5 Fitted curves of relationship between dynamic elastic modulus and amplitude of dynamic strain
由图5和拟合相关系数可知拟合效果良好,这表明式(4)~(6)适合描述改良土应力与应变骨干关系以及动弹性模量随应变幅值变化的规律。
2.1.2 加载频率和围压对初始动弹性模量的影响
初始动弹性模量E0和频率f以及围压σ3之间的关系曲线见图6。从图6可看出:在相同频率f作用下,改良土的初始动弹性模量E0随围压σ3的增大而增大;在同一围压σ3作用下,初始动弹性模量E0随加载频率f增大而增大。这表明围压和加载频率均对改良土的初始动弹性模量产生较大影响。经分析可知:围压越大,试样受到的侧向约束越大,其轴向越难产生变形,在相同动应力幅值作用下,根据式(4)计算得到E0也越大。在等幅循环荷载作用下,频率越高意味着加载速率越大[19]。而加载速率越大,岩土体材料表现出的黏性也越显著,此时,加载方向上的变形往往来不及产生,瞬时变形较小,宏观上表现为瞬时动弹性模量增大或者初始动弹性模量随加载频率增大而增大。

图6 初始动弹性模量、围压与加载频率之间的关系
Fig. 6 Relationship among initial dynamic elastic modulus, confining pressure and loading frequency
2.2 阻尼比试验结果及分析
2.2.1 阻尼比与动应变幅值的关系
图7所示为频率f=1 Hz时,阻尼比随动应变幅值变化的曲线。从图7可看出:阻尼比随动应变幅值的增大而增大,但增大速率逐渐变小并趋于稳定,曲线形态近似为双曲线形式。阻尼比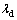 和应变幅值
和应变幅值 之间的拟合关系可用如下的双曲线函数式表示[19]:
之间的拟合关系可用如下的双曲线函数式表示[19]:
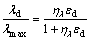 (8)
(8)
式中: 为最大阻尼比;
为最大阻尼比; 为拟合参数。
为拟合参数。
从图7可看出:当频率和动应变幅值相同时,围压越大,阻尼比越小。经分析可知:围压越大,试样颗粒间挤压越密实。从波动传播理论看,这有利于减少土颗粒间振动传递路径和时间,也减小了颗粒间产生摩擦滑移的可能性,从而减少了能量耗散,宏观上表现为黏性耗散机制退化,而材料的黏性耗散能力越强,阻尼比越大。
拟合参数 和
和 见表3,典型的改良土阻尼比随动应变幅值变化的拟合曲线见图8。拟合相关系数为0.98,拟合效果良好,拟合关系式为
见表3,典型的改良土阻尼比随动应变幅值变化的拟合曲线见图8。拟合相关系数为0.98,拟合效果良好,拟合关系式为
 (9)
(9)

图7 阻尼比与动应变幅值关系曲线
Fig. 7 Relationship between damping ratio and amplitude of dynamic strain
表3 不同频率时的参数 和
和
Table 3 Parameters of  and
and  for different frequencies
for different frequencies

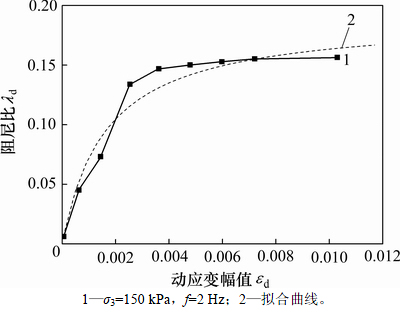
图8 阻尼比与动应变幅值的拟合关系
Fig. 8 Fitted relationship between damping ratio and amplitude of dynamic straing
2.2.2 围压和加载频率对阻尼比的影响
最大阻尼比与围压、加载频率的关系见图9。由图9和表3可知:当动应变幅值和频率相同时,最大阻尼比随围压增加而减小,而当动应变幅值和围压相同时,最大阻尼比随加载频率发生变化的幅度很小。与加载频率相比,围压是影响改良土最大阻尼比的主要因素。
2.3 动强度试验结果及分析
动应力强度 和相应的破坏振次
和相应的破坏振次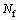 之间的关系见图10。从图10可看出:围压越大,相同破坏振次对应的动应力强度越大。即在相同围压下,破坏振次越大,动应力强度越小。
之间的关系见图10。从图10可看出:围压越大,相同破坏振次对应的动应力强度越大。即在相同围压下,破坏振次越大,动应力强度越小。
根据图10的变化规律,采用下式描述动应力破坏强度与破坏振次之间的关系:
 (10)
(10)

图9 最大阻尼比与加载频率以及围压之间的关系
Fig. 9 Relationship among damping ratio,confining pressure and loading frequency

图10 动应力强度与破坏振次的关系
Fig. 10 Relationship between dynamic stress failure strength and corresponding cycle times
式中: 和
和 为拟合参数。拟合参数
为拟合参数。拟合参数 和
和 见表4。从图10可看出:拟合结果和试验结果相差不大,即式(10)的拟合效果良好。
见表4。从图10可看出:拟合结果和试验结果相差不大,即式(10)的拟合效果良好。
2.4 动力累积变形试验结果及分析
当围压 kPa,频率
kPa,频率 Hz,动静应力比k为0.5, 0.6和0.8时,试样的轴向动力累积应变和循环作用次数的关系曲线见图11。
Hz,动静应力比k为0.5, 0.6和0.8时,试样的轴向动力累积应变和循环作用次数的关系曲线见图11。
从图11可看出:当围压和频率一定时,动静应力比越大,改良土和未改良土的累积应变越大;对于改良土,轴向累积动应变随振动次数增加而逐渐增加;随着振动次数增加,轴向累积动应变曲线逐渐变得平缓,即轴向累积应变速率逐渐减小。根据文献[20],本文试验中改良土的累积变形发展是稳定的。
表4 不同 时的参数
时的参数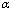 和
和
Table 4 Parameters of 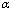 and
and  at different
at different 


图11 动力累积应变与循环作用次数的关系
Fig. 11 Relationship between dynamic cumulative strain and corresponding cycle times
2.5 改良效果评价
2.5.1 动弹性模量
从图3和图6可看出:当围压为100 kPa,频率为1 Hz时,改良土的动弹性模量均比未改良土的大。未改良土和改良土的初始动弹性模量分别为14.7 MPa和21.2 MPa。与未改良土相比,水泥改良泥质板岩土的初始动弹性模量增加44%,这表明经水泥改良后,泥质板岩土的刚度显著提高。
2.5.2 阻尼比
从图9可看出:当围压为150 kPa,频率分别为1,2和4 Hz时,未改良土最大阻尼比分别为0.29,0.28和0.29,而改良土的最大阻尼比分别为0.29,0.26和0.27,可见水泥改良对泥质板岩土的最大阻尼比影响不大。
2.5.3 动强度
从图10可看出:当围压为100 kPa,加载频率为1 Hz时,未改良土的动强度曲线均在改良土的下方。即在相同破坏振次作用下,改良土动力强度均比未改良土的大。因此,水泥改良后,泥质板岩土的强度显著提高。
2.5.4 动力累积变形
从图11可看出:当围压、频率以及动静应力比一定时,未改良土的累积应变比改良土的大,且两者间的差值随循环次数增加而显著增大。例如对于k = 0.6的试验,N=200时未改良土的累积应变达0.210,仍然比N=2 000时改良土的累积应变0.154大很多。这是因为未改良土的累积变形曲线在较低循环次数作用下快速上升,如对于k = 0.5的试验,当N由10增加到50时,累积变形由0.007增加到0.015,增加了约1倍;而当N=200时,累积变形快速增加到0.180,相对N=50时,累积变形增大了10倍以上。可见,未改良土的累积变形速率呈增大趋势。根据文献[20],本文试验中未改良土的累积变形发展是不稳定的。结合前面对改良土累积变形特点分析可知,水泥改良后,泥质板岩土动力变形显著减小,动力变形发展的稳性显著增强。
本文试验的泥质板岩砂土中主要含白云母、绿泥石等亲水矿物,不排水条件下土中矿物互层结构、颗粒定向结构等较容易破坏以及产生崩解现象。在循环动荷载反复作用下,土内部联结结构进一步变得松散、紊乱,颗粒间发生不可逆的滑移也进一步增大,同时,大颗粒逐渐变成小颗粒,矿物颗粒进一步发生崩解,土颗粒间的有效承载力急剧下降,这导致土体内产生的累积变形不断增大,且累积变形速率越来越大。因此,泥质板岩土的刚度、强度以及动力变形稳定性等均较差。而水泥改良土中土颗粒通常被水泥凝胶吸附包裹,同时土颗粒中的孔隙中填充于大量纤维状结晶中,构成了一定的水泥胶结网络格架作用,形成了水泥土骨架。由于水泥骨架的弹性模量、强度等较高,水泥胶结网又能有效抑制土中矿物颗粒的膨胀变形和崩解软化,因此,与未改良土相比,水泥改良泥质板岩土的刚度、强度以及动力变形稳定性均显著提高。
3 结论
1) 改良土应力应变骨干曲线关系为双曲线函数关系。动弹性模量随动应变幅值增加而减小。阻尼比随动应变幅值增加而增大,它们之间关系近似为双曲线函数关系。
2) 围压是影响改良土初始动弹性模量以及最大阻尼比的主要因素。初始动弹性模量随围压增大而增大,而最大阻尼的变化规律刚好相反。加载频率对初始动弹性模量有重要影响,对最大阻尼比的影响不大。初始动弹性模量随加载频率增大而增大。
3) 改良土的动应力强度随相应的破坏振次增加而降低,且动应力强度和破坏振次的对数之间的关系近似为线性递减关系。
4) 水泥改良效果良好。水泥改良后,泥质板岩土的刚度、强度以及变形稳定性均显著提高。
参考文献:
[1] 徐望国, 张家生, 贺建清, 等. 低灰量水泥土动力特性试验研究[J]. 湖南科技大学学报(自然科学版), 2007, 22(2): 52-56.
XU Wangguo, ZHANG Jiasheng, HE Jianqing, et al. Study on dynamic properties of cement improved soil with low cement content[J]. Journal of Hunan University of Science & Technology (Natural Science Edition), 2007, 22(2): 52-56.
[2] 李池龙. 石灰改良土动弹性模量与阻尼比的试验研究[J]. 路基工程, 2016, 187(4): 125-132.
LI Chilong. Experimental study on dynamic elastic modulus and damping ratio of lime-improved soil[J]. Subgrade Engineering, 2016, 187(4): 125-132.
[3] 雷胜友, 惠会清. 膨胀土及其改良土静动力特性对比分析[J]. 岩石力学与工程学报, 2004, 23(17): 3003-3008.
LEI Shengyou, HUI Huiqing. Dynamostatic analysis of properties of expansive soil and improved soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(17): 3003-3008.
[4] 张向东, 曹启坤, 潘宇. 二灰改良土动力特性试验研究[J]. 岩土力学, 2010, 31(8): 2560-2564.
ZHANG Xiangdong, CAO Qikun, PAN Yu. Experiment research of lime-fly ash Soil’s dynamics characteristics[J]. Rock and Soil Mechanics, 2010, 31(8): 2560-2564.
[5] 段俊彪. 水泥及石灰改良土填料动力特性试验分析[J]. 铁道勘察, 2006(4): 39-41.
DUAN Junbiao. Experimental analysis on dynamics characteristics of cement and lime improved soil refillings[J]. Railway Investigation and Surveying, 2006(4): 39-41.
[6] 王天亮, 刘建坤, 田亚护. 水泥及石灰改良土冻融循环后的动力特性研究[J]. 岩土工程学报, 2010, 32(11): 1733-1737.
WANG Tianliang, LIU Jiankun, TIAN Yahu. Dynamic properties of cement-and lime-improved soil subjected to freeze-thaw cycles[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1733-1737.
[7] 崔伟, 李华銮, 穆乃敏. 石灰改性膨胀土工程性质的试验研究[J]. 岩土力学, 2003, 24(4): 606-609.
CUI Wei, LI Hualuan, MU Naimin. Experimental research on engineering character of improved expansive soil with lime[J]. Rock and Soil Mechanics, 2003, 24(4): 606-609.
[8] 贺建清, 张家生. 石灰土填料动力特性试验研究[J]. 湖南科技大学学报(自然科学版), 2005, 20(4): 58-63.
HE Jianqing, ZHANG Jiasheng. Experimental study on dynamic properties of soft soil treated with lime cyclic loading[J]. Journal of Hunan University of Science & Technology (Natural Science Edition), 2005, 20(4): 58-63.
[9] 赵勇. 泥质粉砂岩化学改良土动力特性测试与分析[J]. 铁道工程学报, 2012, 162(3): 22-25.
ZHAO Yong. Test and analysis of dynamic character of chemical improved soil of argillaceous siltstone for subgrade of high-speed railway[J]. Journal of Railway Engineering Society, 2012, 162(3): 22-25.
[10] 顾欢达, 李翠, 薛国强. MSWI 混合土在动力荷载作用下的变形特性试验研究[J]. 重庆交通大学学报(自然科学版), 2016, 35(3): 38-42.
GU Huanda, LI Cui, XUE Guoqiang. Deformation properties of MSWI mixed soil under cyclic dynamic loading[J]. Journal of Chongqing Jiaotong University (Natural Science), 2016, 35(3): 38-42.
[11] 毛成, 邱延峻. 膨胀土与改性膨胀土的动力特性试验研究[J]. 岩石力学与工程学报, 2005, 24(10): 1783-1788.
MAO Cheng, QIU Yanjun. Testing study on dynamic properties of expansive soil and improved expansive soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(10): 1783-1788.
[12] 杨广庆. 水泥改良土的动力特性试验研究[J]. 岩石力学与工程学报, 2003, 22(7): 1156-1160.
YANG Guangqing. Study of dynamic performance of cement-improved soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(7): 1156-1160.
[13] 董全杨, 蔡袁强, 徐长节, 等. 干砂饱和砂小应变剪切模量共振柱弯曲元对比试验研究[J]. 岩土工程学报, 2013, 35(12): 2283-2289.
DONG Quanyang, CAI Yuanqiang, XU Changjie, et al. Measurement of small-strain shear modulus σmax of dry and saturated sands by bender element and resonant column tests[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(12): 2283-2289.
[14] 陈正发, 于玉贞. 土工动力离心模型试验研究进展[J]. 岩石力学与工程报, 2006, 25(S2): 4026-4033.
CHEN Zhengfa, YU Yuzhen. A review on development of geotechnical dynamic centrifugal model test[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S2): 4026-4033.
[15] 陈俊桦, 张家生, 李键. 考虑粗糙度的黏性土-结构接触面力学特性试验[J]. 四川大学学报(工程科学版), 2015, 47(4): 22-30.
CHEN Junhua, ZHANG Jiasheng, LI Jian. Experimental research on mechanical characteristics of cohesive soil-structure interface by considering its roughness[J]. Journal of Sichuan University (Engineering Science Edition), 2015, 47(4): 22-30.
[16] 陈俊桦, 张家生, 李键. 接触面粗糙度对红黏土-混凝土接触面力学性质的影响[J]. 中南大学学报(自然科学版), 2016, 47(5): 1682-1688.
CHEN Junhua, ZHANG Jiasheng, LI Jian. Influence of interface roughness on mechanical properties of red clay-concrete interface[J]. Journal of Central South University (Science and Technology), 2016, 47(5): 1682-1688.
[17] 贾厚华. 化学改良土无侧限抗压强度的试验研究[J]. 土工基础, 2010, 24(3): 84-87.
JIA Houhua. Experimental research on unconfined compressive strength for chemical-improved soil[J]. Soil Engineering and Foundation, 2010, 24(3): 84-87.
[18] 颜胜才. 水泥改良土的物理力学特性试验研究[J]. 铁道建筑, 2015(4): 107-109.
YANG Shengcai. Tests on physical and mechanical properties of cement-improved solid[J]. Railway Engineering, 2015(4): 107-109.
[19] 谢定义. 土动力学[M]. 北京: 高等教育出版社, 2011: 102-115.
XIE Dingyi. Soil dynamic[M]. Beijing: Higher Education Press, 2011: 102-115.
[20] 冷伍明, 周文权, 聂如松, 等. 重载铁路粗粒土填料动力特性及累积变形分析[J]. 岩土力学, 2016, 37(3): 728-736.
LENG Wuming, ZHOU Wenquan, NIE Rusong, et al. Analysis of dynamic characteristics and accumulative deformation of coarse-grained soil filling of heavy-haul railway[J]. Rock and Soil Mechanics, 2016, 37(3): 728-736.
(编辑 陈灿华)
收稿日期:2016-10-12;修回日期:2016-12-22
基金项目(Foundation item):国家自然科学基金资助项目(51308210) (Project(51308210) supported by the National Natural Science Foundation of China)
通信作者:陈乐求,博士,副教授,从事岩土工程、路基工程研究;E-mail: 365148895@qq.com