自适应基因表达式程序设计研究及应用
贾丽媛1,张弛2
(湖南城市学院 信息科学与工程学院,湖南 益阳,413000)
摘要:针对基因表达式程序设计(GEP)是基于基因型和表现型的新型遗传算法,它综合了遗传算法(GA)和遗传程序设计(GP) 的优点,但在解决具体问题时有收敛速度较慢、易陷入局部最优和拟合度不高等缺陷,提出一种自适应基因表达式程序设计算法(AGEP),它将差分突变搜索、混沌重组和变异操作、灾变算子运用于GEP中;最后将其应用于实例中,并将其所得结果与传统的基因表达式程序设计结果进行比较。研究结果表明:该算法不仅提高了算法的精度和收敛速度,而且有效地克服了不成熟收敛,理论证明该算法全局收敛;改进的基因表达式程序设计性能良好。
关键词:基因表达式程序设计;差分突变搜索;混沌重组和变异;全局收敛
中图分类号:TN919.81 文献标志码:A 文章编号:1672-7207(2012)06-2210-05
Research and application of an adaptive gene expression programming (AGEP)
JIA Li-yuan1, ZHANG Chi2
(School of Information Science and Engineering, Hunan City University, Yiyang 413000, China)
Abstract: The gene expression programming is a new generic algorithm based on genome and phenomena with many GA (Genetic algorithm) and GP (Genetic programming) merits, but there are many deficiencies, specially its convergence speed is slow, it is easy to fall in local best and its fitting degree is low. An adaptive gene expression programming algbrithm (AGEP) was presented, whose chaos recombination, mutation operation and cataclysm operator were used in GEP. It was used in an application example and its results were compared with those obtained by traditional GEP and an improved GEP. The results show that the new method (AGEP) can overall convergence and it not only increases its precision and convergence speed, but also overcomes premature convergence. Improved AGEP performed better than traditional GEP and an improved GEP.
Key words: gene expression programming; differential mutation search; chaos recombination and mutation; global convergence
基因表达式程序设计(Gene expression programming,GEP)是Ferreira[1]提出的一种基于基因型(Genome)和表现型(Phenomena)的新型遗传算法。GEP的个体是由多个长度固定不定的基因组成的线性串,然后,这些个体被表示成表达式树(Expression trees, ET)。它综合了Genetic algorithm (GA)和Genetic programming(GP)的优点,具有染色体简单、线性和紧凑、易于进行遗传操作等到优点。 它在符号回归、分类和时间序列问题预测中得到广泛应用[2-6],成为一个非常有力的数据挖掘工具。染色体由若干个基因(Gene )通过连接运算符连接组成。Gene由头部(hail)和尾部(tail)组成,hail包含了函数集(Op)和终结符集(Data)元素。设头部长度为h,尾部长度为t,函数中的最大目数为n。
t=h(n-1)+1 (1)
向量xi用于存贮函数集Op和终结符集Data向量的元素,其存贮形式为:
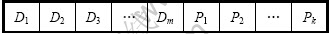
其中:Di∈data;i=1,2,…,m;Pi∈Op ,i=1,2,…,k;Data和Op集合的个数为m+k;数据集Data的个数为m;单基因染色体长度gene_len为h+1。
为方便差分操作向量xi中的m维Data向量,它们用二维数组D[NP][m]保存(其中:NP为种群个数)。
GEP进化过程与传统的遗传算法[2]很相似,每一代通过遗传算子(选择算子、变异算子、倒位算子、重组、变换算子)进化。文献[3]描述了GEP算法的基本框架。
在GEP算法中,根据适应度函数选择出的双亲基因非常接近,因而所产生的后代相对双亲也必然比较接近,所期待的改善程度就较小,这样,基因模式的单一性不仅减慢进化历程,而且可能导致进化停滞,过早收敛于局部最优点,导致算法搜索性能不高。
1 自适应基因表达式程序设计(AGEP)
1.1 基于差分突变的搜索技术
差分演化算法(Differential evolution,DE)是Strom和Price[7]共同提出的,是一种快速的演化算法。它采用实数编码,并利用个体间的差分信息来引导搜索产生新个体。对于差分演化算法,为了区分其方法,使用符号“DE/a/b/c”。其中:DE为算法;a为突变的向量(可以是随机或最佳向量);b为差分向量的个数;c为指交叉方案(二项式或指数)。变异策略“DE/rand/1” 是一个经典的战略[7],按下列方式产生中间向量vi:
vi=xr1+F·(xr2-xr3) (2)
在方程(2)中,r 1,r 2,r3∈{ 1,…,NP };r1≠r2≠r3≠i;xr2-xr3为差分向量,在进化过程中,它能够自适应地调整搜索方向和搜索步长;F为缩放因子。然而,若能够更多地启发式控制搜索方向,则差分进化性能可以明显提高。为此,提出一个新的搜索技术。获得di,j的方法如下:
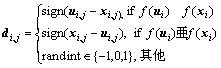 (3)
(3)
其中:di,j为第i个目标向量的第j维搜索向量;sign(·)为向量的搜索控制符号函数,同时randint∈{1,0,1 }意味着di,j从{-1,0,1 }中随机生成。di,j=1表明从正方向搜索,di,j=-1表明从负方向搜索,di,j=0表明仍停留在它的基向量第j维方向;ui为目标向量的试验向量(不同于xi)。式(3)表明:当试验向量优于其目标向量时,将获得好的搜索方向;若试验向量劣于其目标向量,则下一代搜索方向相反。结合di为目标向量的搜索向量,修改式(2)如下:
vi=xr1+F·di·|xr2-xr3| (4)
为了控制GEP的搜索方向,对每个目标向量的Vi采用方程(4)方法进行。注意向量Vi中第j维的搜索向量di,j初始化值取集合{1,0,1}中元素。
1.2 混沌(Logistic映射)重组和变异算子
传统的基因重组和变异操作在算法整个搜索过程中都保持不变,这不利于算法性能的提高。为此,把混沌理论运用到基因重组和变异操作中,通过混沌序列动态地控制基因重组和变异操作,将提高基因重组和交叉操作的效率。在初始阶段,适应度低于平均适应度,说明该个体性能不好,对它采用较大的基因重组概率pr和变异概率pm;在后期阶段,适应度高于或接近平均适应度,说明该个体性能优良,对它采用较小的pr和pm。利用Logistic映射作为混沌信号发生器,产生一个迭代序列[8],pr序列初始、中期和后期阶段分别在[0.5,0.7],[0.3,0.5]和[0.1,0.2]之间变化,pm序列初始、中期和后期阶段分别在[0.06,0.07],[0.03,0.06]和[0.02,0.03]之间变化。同时,也用混沌序列来控制基因重组点和变异点的选择。
1.3 灾变算子
GEP算法的局部搜索能力较强,但是,很容易陷入局部极值。灾变的思想是[9]:在进化过程中,往往有前途的个体(全局是最优个体)适应度小于当前最佳适应度,容易被淘汰。所以,要跳出局部极值就必须杀死当前部分优秀个体,从而让远离当前极值的点有充分的进化余地。在种群适应度保持在稳定值一段时间后,发生灾变,杀掉最优秀的个体,这样才可能产生更优秀的物种。AGEP进行灾变时用灾变倒计数的概念,倒计数的长度取决于进化的速度,进化速度越慢,倒计数长度越长。当倒计数完毕还没有新的最优值时,便认为局部搜索已经充分,就发生灾变[10-15]。若若干次灾变后产生的个体的适应度与没灾变前的一样,则停止灾变。
1.4 算法设计
算法如下:
PROCEDURE AGEP算法
Begin
随机初始化种群P(0),同时初始化dij;
计算P(0)中个体xi的适应度;
t:=0;
repeat;
按式(10)执行差分突变搜索产生中间个体vi ,组成P(t)一部分;
执行混沌重组、变异操作来重组P(t);
执行IS和RIS变换操作来重组P(t);
计算P(t) 中个体的适应度;
根据选择策略从P(t) 中选择生成下一代父体P(t+ 1);
执行灾变操作
t:= t+ 1;
until 满足停止条件;
用P(t)中的最好个体进行系统预测;
End
2 实验及结果
2.1 实验参数设置
针对本文改进的AGEP在函数优化中的应用数据,以VC++和Matlab为实验平台。输入一组回归数据,具有2个输入变量x和y以及1个输出变量z。算法通过已知的输入输出数据进行建模,再利用建立的模型算出预测值,计算真实值与预测值的相对误差。分别对常规GEP算法、改进GEP算法[11]和本文的AGEP算法进行检验,比较和分析其结果。
设置进化算子:进化代数为1 000,种群大小为50,基因数为5,头部长度为6,IS和RIS变换率为0.1,单点重组、2点重组率pr和变异率pm采用混沌概率;函数集为{+,-,*,/,sqrt,ln,sin,cos,tan};适应度函数:均方差,随机数取值范围为[-10, 10]。差分突变算子中的Fi和CRi采用文献[8]中的参数。
2.2 实验
由AGEP 对表1数据计算多次得到的较好模型为:
Z=9.346((tan(xy)-((2x)))+(3.689 7)×(5.920 26)+
2(((cos(t(((-0.368 97)+y2))))1/2×(-5.179 27))/
(2.446 67))–sin(x2+2.590y)-(ln(2.314 56+x)-
3.622 08)/sin(cos(x+y))+(7.526 4)×
tan(((cos(sin(((4.23x)+y)))×(5.178 0))/(x+y/x))+
3.698 7sin(tan((y-2.23176))))
将AGEP算法运算后得到的预测值与GEP和文献[11]中改进的GEP进行对比实验,结果如表2所示。
表1 实验参数
Table 1 Experimental parameters
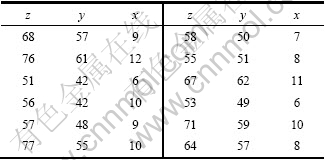
表2 AGEP和GEP、改进的GEP[11]实验结果比较
Table 2 Comparison of experimental results among GEP and improved GEP[11] and AGEP
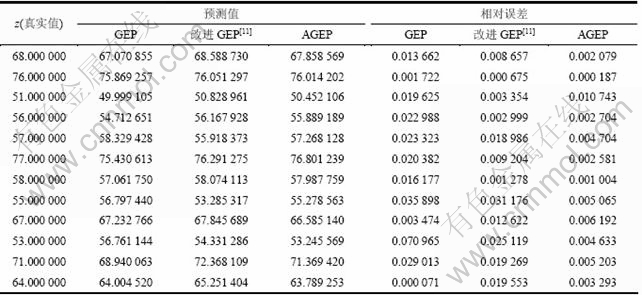
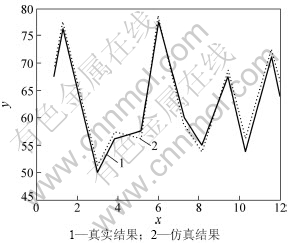
图1 AGEP算法的运算结果
Fig.1 Operational results of AGEP
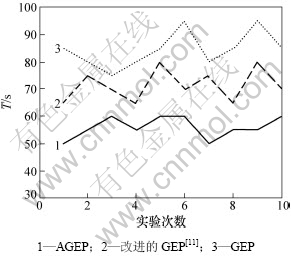
图2 AGEP和GEP与改进的GEP[11]的时耗比较
Fig.2 Comparison of time consumption among GEP and improved GEP[11] and AGEP
从表2可见:GEP比GEP和文献[11]中改进的GEP算法性能要好,AGEP算法的平均误差约为文献[11]中改进的GEP算法的1/5,约为基本GEP算法的1/20。从图2可见:在10次实验中AGEP每次的收敛速度都比文献[11]中的GEP和GEP的收敛速度快,说明AGEP算法具有更好的收敛性能、鲁棒性和更高的运算精度。
3 结论
(1) 提出一种自适应基因表达式程序设计算法(AGEP),设计了适合基因表达式特点的差分突变搜索、混沌重组、变异算子和灾变算子。
(2) 此方法能提高算法的收敛速度、精度,有效克服算法陷入局部最优,以达到全局最优。
参考文献:
[1] Ferreira C. Gene expression programming a new adaptive algorithm for solving problems[J]. Complex Systems, 2001, 13(2): 87-129.
[2] 周明, 孙树栋. 遗传算法原理及应用[M]. 北京: 国防工业出版社, 1999: 123-166.
ZHOU Ming, SUN Shu-dong. The principle and application of genetic algorithm[M]. Beijing: National Defense Industrial Press, 1999: 123-166.
[3] 龚文引, 蔡之华. 基因表达式程序设计在复杂函数自动建模中的应用[J]. 系统仿真学报, 2006, 18(6): 1450-1454.
GONG Wen-yin, CAI Zhi-hua. Automatic modeling of complex functions based on gene expression programming[J]. Journal of system simulation, 2006, 18(6): 1450-1454.
[4] 李康顺, 黄浩华, 张文生. 一种基于GEP的多层物流网络Prufer编码优化算法[J]. 系统仿真学报, 2012, 24(3): 594-602.
LI Kang-shun, HUANG Hao-hua, ZHANG Wen-sheng. Prufer code optimization algorithm for muti-layer logistic networks based on gene expression programming[J]. Journal of system simulation, 2012, 24(3): 594-602.
[5] 谷琼, 蔡之华, 朱莉. 基于PCA-GEP算法的边坡稳定性预测[J]. 岩土力学, 2009, 30(3): 758-761.
GU Qiong, CAI Zhi-hua, ZHU Li. Slope stability prediction based on PCA-GEP algorithm[J]. Rock and Soil Mechanics, 2009, 30(3): 758-761.
[6] 王卫红, 阮薇, 李曲. 基于差分演化的GEP决策树算法[J]. 计算机工程, 2011, 37(1): 182-183.
WANG Wei-hong, RUAN Wei, LI Qu. Decision tree algorithm by gene expression programming based on differential evolution[J]. Computer Engineering, 2011, 37(1): 182-183.
[7] Storn R, Price K. Differential evolution—A simple and ef?cient heuristic for global optimization over continuous spaces[J]. J of Global Optim, 1997, 11(4): 341-359.
[8] Bezdek J C. What is computational intelligence computational intelligence imitationg life[M]. New York: IEEE Press, 1994: 202-205.
[9] Russell S, Norvig P. 人工智能现代方法[M]. 姜哲, 等译. 北京: 人民邮电出版社, 2004: 105-106.
Russell S, Norvig P. A artificial intelligence modern approach[M]. JIANG Zhe, et al, trans. Beijing: The People Post and Telecommunications Press, 2004: 105-106.
[10] Cai Z. Disciplinary frame and general features for intelligence science[C]// Proc 1st China-Korea Joint Workshop on Intelligent Systems. Korea, 2002: 214-219.
[11] 张春潜, 王洪亮, 武江伟. 一种改进的GEP算法在函数优化中的运用[J]. 兵工自动化, 2010, 29(4): 90-94.
ZHANG Chu-qian, WANG Hong-liang, WU Jiang-wei. Application of an improved GEP algorithm on function optimization[J]. Ordnance Industry Automation, 2010, 29(4): 90-94.
[12] Brest J, Greiner S, Boskovic B, et al. Adapting control parameters in differential evolution: A comparative study on numerical benchmark problems[J]. IEEE Trans on Evol Comput, 2006, 10(6): 646-657.
[13] 朱红求, 阳春华, 桂卫华. 一种带混沌变异的粒子群优化算法[J]. 计算机科学, 2010, 37(3): 216-218.
ZHU Hong-qiu, YANG Chun-hua, GUI Wei-hua. Particle swarm optimization with chaotic mutation[J]. Computer Science, 2010, 37(3): 216-218.
[14] 毛润宇, 王小平, 薛小平. 一种自适应差分演化算法[J]. 计算机应用与软件, 2008, 25(12): 7-26.
MAO Run-yu, WANG Xiao-ping, XUE Xiao-ping. An adaptive differential evolution algorithm[J]. Computer Applications and Software, 2008, 25(12): 7-26.
[15] 郭俊, 桂卫华, 阳春华. 改进差分进化算法在铝电解多目标优化中的应用[J]. 中南大学学报: 自然科学版, 2012, 33(1): 45-48.
GUO Jun, GUI Wei-hua, YANG Chun-hua. An improved hybrid differential evolution algorithm used for multi-objective optimization of aluminum[J]. Journal of Central South University: Science and Technology, 2012, 33(1): 45-48.
(编辑 陈灿华)
收稿日期:2011-07-15;修回日期:2011-09-28
基金项目:湖南省科技计划项目(2011FJ3016);湖南省教育厅教改项目([2009]321)
通信作者:贾丽媛(1972-),女,湖南益阳人,硕士,副教授,从事人工智能和演化计算研究;电话:13607371186;E-mail:jia_4211003@126.com