DOI: 10.11817/j.issn.1672-7207.2016.07.014
基于集成固有时间尺度分解和谱峭度的滚动轴承故障检测
向玲,鄢小安
(华北电力大学 机械工程系,河北 保定,071003)
摘要:针对固有时间尺度分解(ITD)方法中固有旋转分量存在局部波动的问题,提出一种集成固有时间尺度分解,将其结合谱峭度法,提高轴承故障检测的准确度。首先运用3次样条插值拟合基线控制点,实现振动信号的自适应频带划分,获得若干个固有旋转分量;然后根据K-L散度准则选取真实分量进行信号重构,使用谱峭度法确定带通滤波器的最优参数;最后分析滤波处理结果的包络谱,得到振动信号的特征信息。研究结果表明:与经验模式分解和单纯包络谱分析方法相比,采用集成固有时间尺度分解和谱峭度的包络方法(EITD-SK)能更好地提取滚动轴承故障特征信息,实现轴承故障的准确检测,结果与实际相符。
关键词:固有时间尺度分解;谱峭度;K-L散度;滚动轴承;故障检测
中图分类号:TH17 文献标志码:A 文章编号:1672-7207(2016)07-2273-08
Fault detection of rolling bearing based on ensemble intrinsic time-scale decomposition and spectral kurtosis
XIANG Ling, YAN Xiaoan
(School of Mechanical Engineering, North China Electric Power University, Baoding 071003, China)
Abstract: Aimed at the problems of local fluctuations of proper rotation component in intrinsic time-scale decomposition (ITD), an ensemble intrinsic time-scale decomposition (EITD) method was proposed. Combining this method and spectral kurtosis (EITD-SK), the precision of bearing fault detection was improved. Firstly, the frequency band of vibration signal was adaptively separated and several proper rotation components was achieved by using cubic spline interpolation to fit baseline control points. Then the real proper rotation components selected by K-L divergence criterion were used to reconstruct the faulty signal, and the optimal band-pass filter parameters were determined by using spectral kurtosis method. Finally, envelope spectrum of the filtered reconstruction signal was analyzed to obtain the characteristic information of the vibration signal. The results show that the proposed method (EITD-SK) performs better in extracting the bearing fault feature information and detecting the bearing fault type than the empirical mode decomposition (EMD) and pure spectral envelope analysis. The analysis result can better agree with the practice.
Key words: intrinsic time-scale decomposition; spectral kurtosis; K-L divergence; rolling bearing; fault detection
滚动轴承作为现代机械设备关键支撑构件,其工作状态与机械传递系统的性能联系紧密。当滚动轴承存在局部损伤时,会受到周期循环振动冲击的影响,其特征通常呈现为非平稳特征,在很大程度上影响着设备的正常工作,甚至带来灾难性事故。因此,有效检测轴承局部缺陷并识别故障类型对机械设备安全稳定工作具备重要现实意义[1]。FREI等[2]提出一种固有时间尺度分解(intrinsic time-scale decomposition, ITD)方法,其能够实现非线性非平稳信号的自适应划分,得到若干个瞬时特征意义明确的单分量信号,即固有旋转分量(proper rotation component, PRC)。文献[2]分析了ITD与典型经验模式分解(empirical mode decomposition,EMD)[3]之间的差异性,经研究发现,ITD较EMD在边界处理和计算效率等方面更具优势,但ITD运用线性变换法进行振动信号频域划分,致使PR分量的波形幅值发生局部波动现象,有失准确性。针对这一缺陷,融合3次样条插值和ITD中的线性变换法,提出一种集成固有时间尺度分解(ensemble intrinsic time-scale decomposition, EITD)方法,该方法能有效抑制边界飞翼现象,克服了PR分量的局部波动缺陷,提高了振动信号分解的准确度和计算效率。谱峭度法(spectral kurtosis, SK)最早由DWYER提出,用来检测含噪信号中的瞬态成分,后来被引用到故障诊断领域[4]。目前国内外学者对谱峭度法开展了一定研究工作。比如,SAWALHI等[5]运用最小熵解卷积剔除原信号噪声干扰,并引入谱峭度法对轴承损伤进行增强检测。蔡艳平等[6]采用EMD和谱峭度相结合的包络解调法提取滚动轴承故障特征,从而判断故障类型。石林锁等[7]将基于WVD的谱峭度法作为检测工具提取滚动轴承的振动特征。上述方法虽然丰富了谱峭度在故障诊断中的应用,但对于低信噪比信号的故障诊断仍无能为力[8]。包络分析法是目前滚动轴承故障诊断中常用的振动信号分析方法[9],但其带通滤波器参数的选取是1个难题。针对上述问题,本文作者将EITD方法和谱峭度相结合,根据K-L散度准则选取PR分量并进行重构,利用重构信号的快速谱峭图构造最优带通滤波器,克服了单纯包络分析法带通滤波器参数选取的难题。采用的方法与经验模态分解(EMD)和单纯包络解调分析相比,能增强并突出轴承微弱冲击特征,提高轴承故障检测的精确度。
1 EITD方法
1.1 ITD方法
ITD具备类似经验模式分解的自适应频带划分性能。若某个非平稳振动信号为Xt,ITD法能实现Xt自高频至低频的逐步分解,得到若干个瞬时特征意义明确的单分量信号,即固有旋转PR分量。ITD的定义如下[10]。
1) 首先运用算子L得出低频基线信号(L为变量,在分解过程中会随着原信号Xt的局部极值点的变化而变化),将原信号与基线信号的差值运算结果当作得到的1个PR分量,非平稳振动信号Xt的1次分解为
 (1)
(1)
式中:Lt为基线信号;Ht为PR分量。
2) 提取信号{Xt, t≥0}的局部极值点Xk及相应时刻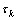 {k=1, 2, …, M},M为极值点总数,设置
{k=1, 2, …, M},M为极值点总数,设置 。
。
3) 在连续极点间隔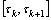 上定义分段线性基线提取算子L为
上定义分段线性基线提取算子L为
 (2)
(2)
 (3)
(3)
式中:0< <1。为提高分解质量,取
<1。为提高分解质量,取 。
。
4) 同样设置1个PR分量提取算子,则 是分解得到的第1个PR分量(即高频振动分量)。将基线信号视为给定信号,重复上述步骤,直至基线信号变为单调函数或常函数。至此,给定信号被划分为
是分解得到的第1个PR分量(即高频振动分量)。将基线信号视为给定信号,重复上述步骤,直至基线信号变为单调函数或常函数。至此,给定信号被划分为

 (4)
(4)
式中: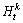 为第
为第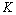 个PR分量;
个PR分量;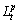 为残余成分。
为残余成分。
1.2 EITD方法
ITD主要运用线性变换原理提取基线信号,将引起PR分量的局部波动,有失分解的准确性。EMD采用插值拟合包络的方法得到若干分解分量,但其具备过包络、欠包络等不足。针对以上问题,本文提出一种集成固有时间尺度分解(ensemble intrinsic time-scale decomposition, EITD)方法,其实现步骤如下:
1) 提取信号Xt全部局部极值点,参考ITD法中的式(2)和式(3)得到各基线控制点Lk。
2) 运用镜像对称法处理信号Xt的边界数据,得到左、右两边界极值点 ,
, ,取k分别为0和
,取k分别为0和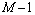 ,参考式(2)和式(3) 得到
,参考式(2)和式(3) 得到 与
与 取值。然后运用3次样条插值拟合全部
取值。然后运用3次样条插值拟合全部 ,获取基线信号
,获取基线信号 。
。
3) 将基线信号与给定信号作差值运算获得 ,即
,即
 (5)
(5)
 为EITD分解时得到的第1个PR分量,即
为EITD分解时得到的第1个PR分量,即 =
= ,若
,若 不符合PR分量条件,即基线
不符合PR分量条件,即基线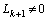 ,则把
,则把 当作给定信号重复上述步骤,循环k次,直至
当作给定信号重复上述步骤,循环k次,直至 为第1个固有旋转分量为止,即
为第1个固有旋转分量为止,即 =
= ,为提高计算效率,需设置1个变量
,为提高计算效率,需设置1个变量 使得满足
使得满足 ≤
≤ 时迭代停止。
时迭代停止。
4) 将 与给定信号作差值运算获得第1个新信号
与给定信号作差值运算获得第1个新信号 ,即
,即
 (6)
(6)
5) 再将 作为给定信号重复上述步骤,得到
作为给定信号重复上述步骤,得到 满足PRC条件的第2个分量
满足PRC条件的第2个分量 ,继续循环
,继续循环 次,获得
次,获得 符合PRC要求的n个PR分量即
符合PRC要求的n个PR分量即 ,直至
,直至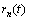 呈现单调趋势或常值为止,最终给定信号
呈现单调趋势或常值为止,最终给定信号 被自适应划分为n个固有旋转分量
被自适应划分为n个固有旋转分量 和1个单调函数
和1个单调函数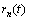 之和,即
之和,即
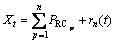 (7)
(7)
EITD中存在1个关键问题,即如何选择合适的迭代停止准则 ,这与EITD的分解质量及计算效率精密相连,目前存在的停止准则主要包括标准差法、三参数法[11]等。为获得瞬时特征具有明确物理意义的PR分量,本文运用三参数法得到
,这与EITD的分解质量及计算效率精密相连,目前存在的停止准则主要包括标准差法、三参数法[11]等。为获得瞬时特征具有明确物理意义的PR分量,本文运用三参数法得到 的准确值。经相关研究发现[12],当
的准确值。经相关研究发现[12],当 小于某区间数值(式中
小于某区间数值(式中 表示第
表示第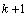 个基线控制点,
个基线控制点, 表示第
表示第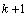 个极值点),即
个极值点),即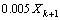 <
< <
< 时,EITD迭代筛选的分量满足PR分量条件,此时获得的分解分量更贴近真实单分量信号。
时,EITD迭代筛选的分量满足PR分量条件,此时获得的分解分量更贴近真实单分量信号。
为考察EITD的分解性能,构造仿真信号 为
为

 (8)
(8)
仿真信号x(t)是调幅-调频分量和余弦函数的混合叠加,其时域波形如图1所示。图2和图3所示分别是信号x(t)经ITD和EITD分解得到的结果。其中前2分量对应信号x(t)中的真实分量,最后1个分量为残余项。
从图2和图3可见:EITD分解结果与信号x(t)的真实单分量相吻合,而ITD分解结果中第2个PR分量存在波形局部波动现象,偏离实际曲线,有失准确性。经比较分析,EITD融合3次样条插值法进行曲线拟合,既能提高波形分解质量,又能克服ITD基于线性变换法计算基线而致使PR分量局部波动的缺陷。因此,EITD能准确揭示多分量信号中单组分的瞬时物理意义,具有较好的工程应用价值。

图1 信号x(t)的时域波形
Fig. 1 Time-domain waveform form of the signal x(t)

图2 信号x(t)经ITD分解的结果
Fig. 2 Results of the signal x(t) obtained by ITD
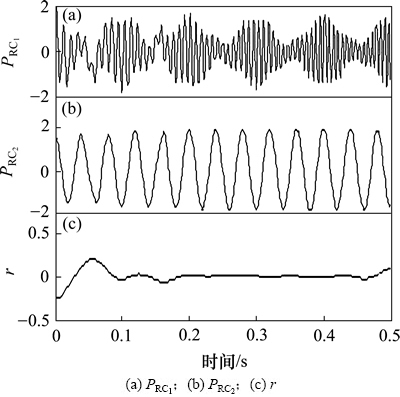
图3 信号x(t)经EITD分解的结果
Fig. 3 Results of the signal x(t) obtained by EITD
1.3 K-L散度准则
信号经EITD分解处理时,存在一定的插值拟合误差。随着分解迭代过程的继续,误差也将逐步累积,从而引起分解过程中产生虚假分量的缺陷,此时需要一种方法来剔除虚假分量,提取有用的真实分量。K-L散度[13]又称相对熵,用来度量2个概率分布的差别。基于此,本文将K-L散度用来衡量各PR分量与原信号的紧密程度。K-L散度越小,表示PR分量与原信号关系越紧密,反之,表示PR分量与原信号越疏远,因此,本文设定1个阈值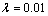 ,将K-L散度小于
,将K-L散度小于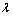 的PR分量视为真实分量,予以保留;K-L散度大于
的PR分量视为真实分量,予以保留;K-L散度大于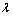 的PR分量视为虚假分量,予以剔除。K-L散度的具体定义如下[14]。
的PR分量视为虚假分量,予以剔除。K-L散度的具体定义如下[14]。
假设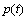 和
和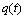 分别为2信号的概率分布,则两者的K-L距离为
分别为2信号的概率分布,则两者的K-L距离为
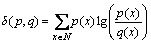 (9)
(9)
由式(9)可定义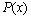 和
和 的散度为
的散度为
 (10)
(10)
2 基于EITD和谱峭度的滚动轴承故障检测
在采用谱峭度分析之前对信号进行一些预处理可以对故障诊断得更精确。比如,苏文胜等[15]采用EMD降噪的预处理方法,提高了谱峭度法的诊断精度。彭畅等[16]采用EEMD降噪的预处理方法,验证了预处理后谱峭度法诊断的有效性。本文利用EITD方法对信号进行预处理,并结合谱峭度法实现滚动轴承故障的有效检测。图4所示为所提方法的整体框架流程图,其具体过程可描述如下:
1) 利用EITD方法对故障信号分解。
2) 分别计算分解得到的各PR分量与原故障信号的互相关系数和各自的K-L散度。
3) 采用相关性准则和K-L散度准则相结合的方法自动提取敏感PR分量重构原故障信号。
4) 计算重构信号的快速峭度图,将其最大峭度处的载波频率和带宽当作滤波器的最优滤波参数对重构信号进行降噪处理。
5) 对滤波后的重构信号进行平方包络谱分析。
6) 将包络谱中峰值频率与滚动轴承故障特征频率进行比较,从而判断故障类型。
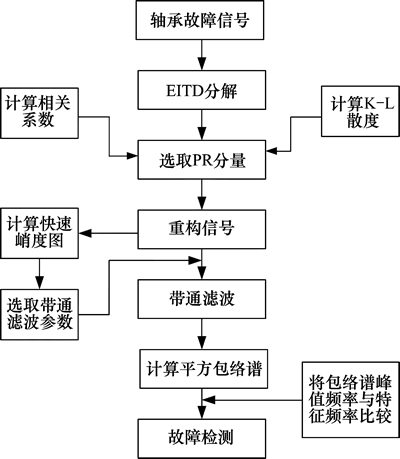
图4 滚动轴承故障检测的框架流程图
Fig. 4 Flow chart of rolling bearing fault diagnosis
3 仿真信号分析
采用滚动轴承故障仿真模型[17]模拟轴承内圈故障信号,利用 来仿真轴承内圈故障时受到的周期脉冲力。设
来仿真轴承内圈故障时受到的周期脉冲力。设 为单位脉冲力下系统的振动响应,
为单位脉冲力下系统的振动响应, 为时间间隔为0.01s的脉冲信号,
为时间间隔为0.01s的脉冲信号,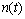 为信噪比为-6 dB的白噪声,采样频率为10 240 Hz,采样点数N=819 2个,转频为12 Hz,内圈故障频率为100 Hz,共振频率为1 000 Hz,
为信噪比为-6 dB的白噪声,采样频率为10 240 Hz,采样点数N=819 2个,转频为12 Hz,内圈故障频率为100 Hz,共振频率为1 000 Hz,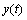 为添加白噪声后的轴承内圈故障信号,具体表达式如下:
为添加白噪声后的轴承内圈故障信号,具体表达式如下:
 (11)
(11)
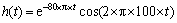 (12)
(12)
 (13)
(13)
图5所示为滚动轴承内圈故障仿真信号,图6所示为滚动轴承内圈故障含噪仿真信号 。首先对信号
。首先对信号 进行EITD分解,分解后的前8个PR分量如图7所示。计算前5个PR分量的相关系数和K-L散度,结果见表1。从表1可见:前3个PR分量的互相关系数较大,且K-L散度小于0.01。根据相关性和K-L散度选取原则,挑选前3个PR分量重构原轴承故障信号,结果如图8所示,计算重构信号的快速峭度图如图9所示。利用谱峭度法选择带通滤波器的最优参数,对滤波后的重构信号进行包络谱分析,分析结果如图10所示。从图10可见:辨识转频(12 Hz)、内圈故障特征频率(100 Hz)及其倍频成分(200,300和400 Hz)等众多特征信息,此外,图10中位于特征频率及倍频处的转频调制边带(88和112 Hz)表现非常明显。
进行EITD分解,分解后的前8个PR分量如图7所示。计算前5个PR分量的相关系数和K-L散度,结果见表1。从表1可见:前3个PR分量的互相关系数较大,且K-L散度小于0.01。根据相关性和K-L散度选取原则,挑选前3个PR分量重构原轴承故障信号,结果如图8所示,计算重构信号的快速峭度图如图9所示。利用谱峭度法选择带通滤波器的最优参数,对滤波后的重构信号进行包络谱分析,分析结果如图10所示。从图10可见:辨识转频(12 Hz)、内圈故障特征频率(100 Hz)及其倍频成分(200,300和400 Hz)等众多特征信息,此外,图10中位于特征频率及倍频处的转频调制边带(88和112 Hz)表现非常明显。
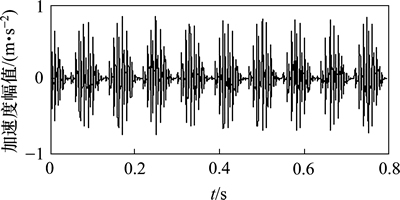
图5 滚动轴承内圈故障仿真信号
Fig. 5 Bearing inner ring fault simulated signal

图6 滚动轴承内圈故障含噪仿真信号
Fig. 6 Bearing inner ring fault simulated signal with noise
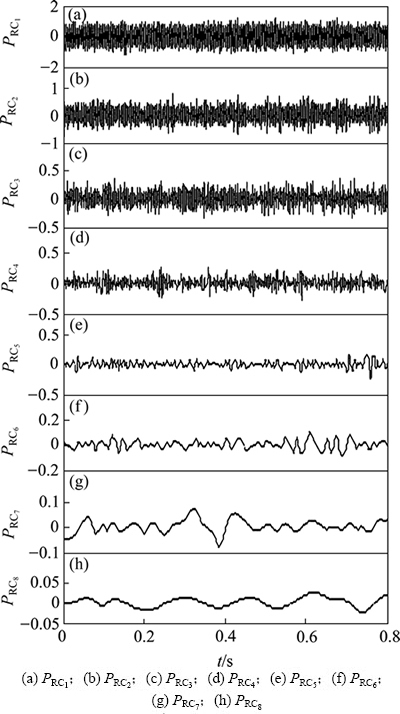
图7 仿真信号y(t)的EITD结果
Fig. 7 EITD results generated from the simulated signal y(t)
表1 相关系数和K-L散度
Table 1 Correlation coefficient and K-L divergence
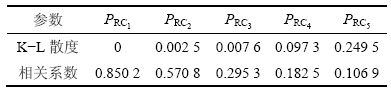

图8 重构信号的时域波形
Fig.8 Time-domain waveform of the reconstruction signal

图9 重构信号的快速峭度图
Fig. 9 Fast kurtogram of the reconstruction signal
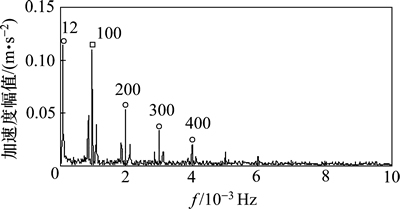
图10 重构信号滤波后的平方包络谱
Fig. 10 Squared envelope spectrum of the filtered reconstruction signal
为验证本文方法的有效性,将滚动轴承内圈故障含噪仿真信号分别经文献[15]中的EMD-SK方法和Hilbert包络解调分析方法[18]处理,所得结果分别如图11和图12所示。虽然从图11和图12中均能辨识出故障特征频率(100 Hz)及转频(12 Hz),但与图10中的计算结果相比较发现,本文所述的方法能够增强故障冲击特征,降低噪声干扰,分析效果更明显。

图11 仿真信号经EMD-SK处理后的包络谱
Fig.11 Envelope spectrum of the simulated signals after EMD-SK processing
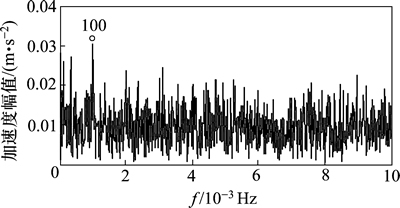
图12 仿真信号的传统包络谱
Fig.12 Traditional envelope spectrum of the simulated signals
4 实验信号分析
以QPZZ实验台为测试对象,在N205轴承内圈上用电火花加工出坑点来模拟点蚀故障。实验台主要由电机、转子、加载器及轴承组成,实验平台与滚动轴承局部损伤图如图13所示。实验中,采样频率为12 800 Hz,工作转速为1 440 r/min,经计算得到内圈故障频率为172 Hz,转频为24 Hz。轴承内圈故障信号的时域波形及频谱如图14所示。
图14中存在峰值很明显的干扰频率成分(239.1 Hz),轴承内圈故障特征频率(172 Hz)不清楚,需要进一步对故障特征进行识别。根据流程图4对故障信号进行分析。首先轴承振动信号经EITD分解得到5个PR分量,各PR分量的相关系数和K-L散度见表2。根据表2选取符合相关性准则且K-L散度小于0.01的PR分量重构轴承故障信号,结果如图15所示。从图15可见:噪声干扰得以减少,共振成分更加突出。图16所示为重构信号的快速峭度图,图16中分解层数为1.5的频带[2 133.33, 4 066.66] Hz范围内谱峭度最大,从而选取带通滤波器的中心频率为3 200 Hz,带宽为2 133.33 Hz,对重构信号进行滤波处理。最终得重构信号经滤波处理后的平方包络谱如图17所示。图17中存在24 Hz的轴转频及其倍频,并且在172 Hz的内圈故障特征频率及其倍频处具有明显峰值,这与实际轴承振动信号的特征分布相吻合,由此验证了本文方法的有效性。

图13 实验平台与滚动轴承局部损伤图
Fig.13 Experimental platform and Partial damage of rolling bearing

图14 内圈故障信号时域波形及频谱图
Fig. 14 Time and spectral diagram of inner-race fault signal
表2 相关系数和K-L散度
Table 2 Correlation coefficient and K-L divergence


图15 重构故障信号的时域波形
Fig.15 Time-domain waveform of the reconstruction signal

图16 重构信号的快速峭度图
Fig. 16 Fast kurtogram of the reconstruction signal
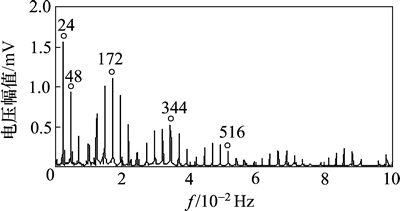
图17 重构信号滤波后的平方包络谱
Fig. 17 Square envelope spectrum of the filtered reconstruction signal
从图17可知:滚动轴承振动信号经EITD分解所得的敏感固有旋转分量保留了丰富的故障频率信息,可以获得滚动轴承振动信号的故障特征。结合EITD和谱峭度法能够使滚动轴承故障特征更加突出,特征信息更加丰富,克服了单纯包络分析法带通滤波器参数选取的难题。
5 结论
1) 针对ITD方法中PR分量出现局部波动的问题,提出一种EITD方法。该方法具有端点效应小、计算速度快、信号分解精度高等优点。
2) 采用EITD与谱峭度相结合的方法提取滚动轴承的故障特征信息,解决了单纯包络分析法带通滤波器参数选取的难题。
3) 仿真和实验结果验证了基于EITD和谱峭度的方法在轴承故障检测中的有效性和优越性,该方法为滚动轴承故障诊断提供了一种新手段。
参考文献:
[1] XIANG Ling, HU Aijun. New feature extraction method for the detection of defects in rolling element bearings[J]. Journal of Engineering for Gas Turbines and Power. 2012, 134(8): 501-507.
[2] FREI M G, OSORIO I. Intrinsic time-scale decomposition: time-frequency-energy analysis and real-time filtering of non-stationary signals[J]. Proceedings of the Royal Society of London A, 2007, 463(2078): 321-342.
[3] HUANG N E, SHEN Z, LONG S R, et al. The Empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London A, 1998, 454: 903-994.
[4] ANTONI J. The spectral kurtosis: a useful tool for characterising non-stationary signals[J]. Mechanical Systems and Signal Processing, 2006, 20(2): 282-307.
[5] SAWALHI N, RANDALL R B, ENDO H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis[J]. Mechanical Systems and Signal Processing, 2007, 21(6): 2616-2633.
[6] 蔡艳平, 李艾华, 石林锁, 等. 基于 EMD 与谱峭度的滚动轴承故障检测改进包络谱分析[J]. 振动与冲击, 2011, 30(2): 167-172.
CAI Yanping, LI Aihua, SHI Linsuo, et al. Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum kurtosis[J]. Journal of Vibration and Shock, 2011, 30(2): 167-172.
[7] 石林锁, 张亚洲, 米文鹏. 基于 WVD 的谱峭度法在轴承故障诊断中的应用[J]. 振动、测试与诊断, 2011, 31(1): 27-31.
SHI Linsuo, ZHANG Yazhou, MI Wenpeng. Application of wigner-ville-distribution-based spectral kurtosis algorithm to fault diagnosis of rolling bearing[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(1): 27-31.
[8] WANG D, PETER W T, TSUI K L. An enhanced Kurtogram method for fault diagnosis of rolling element bearings[J]. Mechanical Systems and Signal Processing, 2013, 35(1): 176-199.
[9] 刘金朝, 丁夏完, 王成国. 自适应共振解调法及其在滚动轴承故障诊断中的应用[J]. 振动与冲击, 2007, 26(1): 38-41.
LIU Jinzhao, DING Xiawan, WANG Chengguo. Adaptive resonanced demodulation method and its applocation to fault diagnosis of freight car rolling bearings[J]. Journal of Vibration and Shock, 2007, 26(1): 38-41.
[10] 罗颂荣, 程军圣, 杨宇. 基于本征时间尺度分解和变量预测模型模式识别的机械故障诊断[J]. 振动与冲击, 2013, 32(13): 43-48.
LUO Songrong, CHENG Junsheng, YANG Yu. Machine fault diagnosis method using ITD and variable predictive model-based class discrimination[J]. Journal of Vibration and Shock, 2013, 32(13): 43-48.
[11] 郑近德, 程军圣, 杨宇. 基于改进的 ITD 和模糊熵的滚动轴承故障诊断方法[J]. 中国机械工程, 2012, 23(19): 2372-2377.
ZHENG Jinde, CHENG Junsheng YANG Yu. A rolling bearing fault diagnosis method based on improved ITD and fuzzy entropy[J]. China Mechanical Engineering, 2012, 23(19): 2372-2377.
[12] 向玲, 鄢小安. 基于小波包的 EITD 风力发电机组齿轮箱故障诊断[J]. 动力工程学报, 2015, 35(3): 205-212.
XIANG Ling, YAN Xiaoan. Fault diagnosis of wind turbine gearbox based on EITD-WPT method[J].Journal of Chinese Society of Power Engineering, 2015, 35(3): 205-212.
[13] 傅祖芸. 信息论[M]. 北京: 电子工业出版社, 2001: 24-27.
FU Zuyun. Information theory[M]. Beijing: Publishing House of Electronics Industry, 2001: 24-27.
[14] 韩中合, 朱霄珣, 李文华. 基于 K-L 散度的 EMD 虚假分量识别方法研究[J]. 中国电机工程学报, 2012, 32(11): 112-117.
HAN Zhonghe, ZHU Xiaoxun, LI Wenhua. A false component identification method of EMD based on kullback-leibler divergence[J]. Proceedings of the CSEE, 2012, 32(11): 112-117.
[15] 苏文胜, 王奉涛, 张志新, 等. EMD 降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]. 振动与冲击, 2010, 29(3): 18-21.
SU Wensheng, WANG Fengtao, ZHANG Zhixin, et al. Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings[J]. Journal of Vibration and Shock, 2010, 29(3): 18-21.
[16] 彭畅, 柏林, 谢小亮. 基于 EEMD, 度量因子和快速峭度图的滚动轴承故障诊断方法[J]. 振动与冲击, 2012, 31(20): 143-146.
PENG Chang, BO Lin, XIE Xiaoliang. Fault diagnosis method of rolling element bearings based on EEMD, measure-factor and fast kurtogram[J]. Journal of Vibration and Shock, 2012, 31(20): 143-146.
[17] 周福昌. 基于循环平稳信号处理的滚动轴承故障诊断方法研究[D]. 上海: 上海交通大学机械与动力工程学院, 2006: 88-89.
ZHOU Fuchang. Research on the fault diagnosis method of rolling element bearing based on cyclostationary signal processing[D]. Shanghai: Shanghai Jiao Tong University. School of Mechanical Engineering, 2006: 88-89.
[18] 黄中华, 谢雅. 基于 Hilbert 变换的滚动轴承内环和外环故障诊断[J]. 中南大学学报(自然科学版), 2011, 42(7): 1992-1996.
HUANG Zhonghua, XIE Ya. Fault diagnosis of roller bearing with inner and external fault based on Hilbert transformation[J]. Journal of Central South University (Science and Technology), 2011, 42(7): 1992-1996.
(编辑 罗金花)
收稿日期:2015-07-19;修回日期:2015-09-19
基金项目(Foundation item):国家自然科学基金资助项目(51475164);河北省自然科学基金资助项目(E2013502226) (Project(51475164) supported by the National Natural Science Foundation of China; Project(E2013502226) supported by Natural Science Foundation of Hebei Province)
通信作者:向玲,博士,教授,从事机械状态监测与故障诊断研究;E-mail: ncepuxl@163.com