文章编号:1004-0609(2008)03-0523-06
钛-氢体系晶体结构和能量的第一原理计算
韩秀丽1,王 清1,孙东立1,张红星2
(1. 哈尔滨工业大学 材料科学与工程学院,哈尔滨 150001;
2. 吉林大学 理论化学计算国家重点实验室,长春 130023)
摘 要:采用基于密度泛函理论的第一原理赝势平面波方法研究了不同钛-氢摩尔比的α-Ti-H和β-Ti-H晶体的稳态几何结构,进行了稳态晶体的总能量计算。结果表明:氢引起α-Ti和β-Ti晶格点阵畸变,晶体体积膨胀。计算得到的不同钛-氢摩尔比的α-Ti-H和β-Ti-H晶体结合能分别小于α-Ti和β-Ti晶体结合能,表明氢原子降低了α-Ti和β-Ti晶体的结合能。氢原子在β-Ti晶体中的占位随氢含量变化,低氢含量时易占据四面体间隙位置,高氢含量时倾向于占据八面体间隙位置。
关键词:钛-氢体系;第一原理;晶体结构;结合能;溶解热
中图分类号:TG 111 文献标识码:A
First-principles calculation of crystal structures and
energies of Ti-H system
HAN Xiu-li1, WANG Qing1, SUN Dong-li1, ZHANG Hong-xing2
(1. School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China;
2. State Key Laboratory of Theoretical and Computational Chemistry, Jilin University, Changchun 130023, China)
Abstract: The equilibrium structures and total energies of α-Ti-H and β-Ti-H crystals with different mole ratios of Ti to H were calculated with the first-principles method based on plane-wave pseudopotential and density function theory. The calculated results show that hydrogen causes the lattice distortion and volume expansion of α-Ti and β-Ti crystals. The calculated binding energies of α-Ti-H and β-Ti-H crystals with different mole ratios of Ti to H are less than those of pure α-Ti and β-Ti crystals, respectively. It reveals that hydrogen atom reduces the binding energies of α-Ti and β-Ti crystals. The calculation results show that the site preference of hydrogen in β-Ti crystal varies with hydrogen content varyiing. Hydrogen is inclined to enter the tetrahedral interstitial site in β-Ti-H crystal with low hydrogen content, and hydrogen is disposed to occupy the octahedral site in β-Ti-H crystal with high hydrogen content.
Key words: Ti-H system; first-principles; crystal structure; binding energy; solution heat
氢是非常敏感的化学元素,很容易与金属发生强烈的发应[1]。长期以来,氢一直被认为是钛合金中的有害元素,由于微量的氢就会使材料产生氢脆和氢致延迟开裂等破坏,因此关于氢在钛合金中行为的研究多集中在氢脆方面[2-4]。然而,近年来大量的研究结果表明[5-11],采用氢处理技术,在钛合金中加入适量氢,可使其热塑性提高,热加工性能得到明显改善。同时,氢处理有助于细化钛合金的显微组织,提高钛合金的综合力学性能。有关钛合金的氢处理工艺、氢处理对钛合金的力学性能、加工性能以及组织结构的影响方面,取得了很多研究成果。由于氢在钛及钛合金中的高活性使得氢在钛合金中的作用机理十分复杂,国内外学者从不同角度和层次对氢致钛合金热塑性机理进行了研究。在早期的研究中,KERR等[12]提出在两相(α+β)钛合金中,氢使塑性较好的β相体积分数增加,从而降低了合金的流变应力。SENKVO等[13]基于钛合金于20~1 100 ℃的弹性模量的实验结果提出了氢致α相软化,氢致β相硬化观点。SONG等[14]采用基于局域密度近似的离散变分方法研究了H、B、C、N和O等元素对α-Ti弹性模量和理论强度的影响。结果表明:氢减小了α相的体模量和理论强度。目前,人们对氢在钛及钛合金中的作用机理仍缺乏系统了解,需要进一步深入研究。利用计算机模拟方法,可以直接从微观角度、电子和原子尺度研究氢在钛中的作用机理,但国内外关于这方面的研究报道甚少。本文作者采用第一原理方法对Ti-H体系的晶体结构和能量进行了计算,研究了氢对钛晶体结构和能量的影响,尝试从原子层面揭示氢在钛晶体中的行为和作用,以期充实和完善现有氢处理理论,揭示氢的作用机理。
1 计算模型与方法
1.1 晶体结构及模型
钛具有两种同素异构体,在882.5 ℃以下为密排六方结构(hcp)的α-Ti晶体,在882.5 ℃至熔点之间为体心立方结构(bcc)的β-Ti晶体。α-Ti的理论晶格常数为:a=0.295 06 nm,c=0.467 88 nm,20 ℃时实验测得的晶格常数为:a=0.295 11 nm,c=0.468 43 nm;β-Ti在900 ℃时实验测得的晶格常数为:a=0.330 65 nm,外推至20 ℃的晶格常数为:a=0.328 2 nm。α-Ti和β-Ti晶格中均存在八面体间隙(O)和四面体间隙(T) 两种类型的间隙位置。已有研究结果表明[14],α-Ti中间隙氢原子占据八面体间隙位置,并引起晶格的四面体发生畸变。本文作者采用超晶胞(Supercell)方法构建了钛与氢摩尔比分别为32?1、16?1和8?1的3种α-Ti-H晶体模型(见图1)。3种超晶胞分别由2×4×2、2×2×2和2×2×1的α-Ti单胞组成,H原子均位于八面体间隙位置,β-Ti中间隙H原子占据何种间隙位置目前尚无定论。本文作者构建了两类β-Ti-H晶体结构模型:第一类模型中H原子位于四面体间隙,钛与氢摩尔比分别为4?1和2?1,超晶胞分别由1×1×2和1×1×1的β-Ti单胞组成(见图2);第二类模型中H原子位于八面体间隙, Ti与H摩尔比同样分别为4?1和2?1(见图3)。
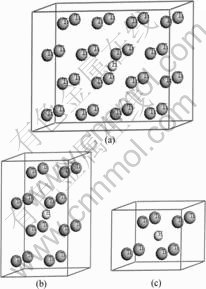
图1 H原子位于八面体间隙的α-Ti-H晶体结构模型
Fig.1 Crystal structure models of α-Ti-H with one H atom at octahedral site: (a) Mole ratio of Ti to H 32?1; (b) Mole ratio of Ti to H 16?1; (c) Mole ratio of Ti to H 8?1

图2 H原子位于四面体间隙的β-Ti-H晶体结构模型
Fig.2 Crystal structure models of β-Ti-H with one H atom at tetrahedral site: (a) Mole ratio of Ti to H 4?1; (b) Mole ratio of Ti to H 2?1

图3 H原子位于八面体间隙的β-Ti-H晶体结构模型
Fig.3 Crystal structure models of β-Ti-H with one H atom at octahedral site: (a) Mole ratio Ti to H 4?1; (b) Mole ratio of Ti to H 2?1
1.2 计算方法
本文作者采用基于密度泛函理论的第一原理计算从头算量子力学程序CASTEP (Cambridge Sequential Total Energy Package)[15]。计算中采用周期边界条件,选取超软赝势和平面波基组展开晶体波函数,平面波截止能量设为310 eV。交换关联能函数采用广义梯度近似(GGA)中的PW91(Perdew-Wang91)形式;布里渊区的k点取样采用Monkhorst-Pack网格,k点取样值为0.4 nm-1;应用高斯能带展宽方法计算费米能,高斯能带展宽值为0.1 eV。
本文作者首先采用BFGS(Broyden Flecher Goldfarb Shanno)算法对构建的α-Ti、β-Ti、α-Ti-H和β-Ti-H晶体结构模型进行全几何优化得到了各晶体的稳态结构。几何优化自洽计算时,体系总能量收敛精度为20 μV/atom,每个原子上的力收敛精度为0.5 eV/nm,位移收敛精度为0.1 fm,应力收敛精度为100 MPa。最后,计算了各稳态晶体的总能量,能量计算时的收敛精度为2 μeV/atom。
2 结果与讨论
2.1 晶格常数和晶体结构
α-Ti和不同Ti与H摩尔比的α-Ti-H晶体完全弛豫后的稳态结构的晶格常数和晶体结构见表1。由于各模型选取的晶胞大小不同,为了便于比较,将计算结果均化为含2个Ti原子的晶胞来处理,同时表中列出了不同Ti与H摩尔比对应的氢含量(质量分数)。由表1可见,几何优化得到的α-Ti晶体的平衡晶格常数为a=0.295 15 nm、c=0.466 66 nm,与文献报道的理论值和实验值吻合很好,相对误差在0.3%以内。几何优化得到的α-Ti-H晶体平衡结构在低氢含量(Ti与H摩尔比为32?1)时仍为密排六方结构,较高氢含量时为稍微变形的密排六方结构,位于八面体间隙的H原子使α-Ti晶格发生畸变,但畸变程度不大。不同Ti与H摩尔比的α-Ti-H晶体的平衡晶格常数a、b、c均大于α-Ti晶体的晶格常数,晶体体积发生膨胀,Ti与H摩尔比为32?1、16?1和8?1的α-Ti-H晶体的体积膨胀率分别为0.12%、0.29%和0.75%。比较不同氢含量的α-Ti-H晶体的计算结果发现,氢含量越高,晶格畸变程度越大,晶体体积膨胀越大,这可在一定程度上解释氢在α-Ti中的有限固溶度问题。由于间隙氢原子溶入α-Ti中后引起晶格畸变和晶体体积膨胀,导致晶体畸变能升高,且α-Ti中溶入的氢原子越多,其畸变能越高,因此,当α-Ti中固溶的氢原子超过一定值后,晶体畸变能过大,晶体结构不稳,从而可能向结构更稳定的钛氢化合物转变。
表1 α-Ti和α-Ti-H晶体的晶格常数和晶体结构的计算结果
Table 1 Calculated results of lattice constants and crystal structures of α-Ti and α-Ti-H crystals

β-Ti和不同Ti与H摩尔比的β-Ti-H晶体完全弛豫后的稳态结构的晶格常数和晶体结构见表2,计算结果同样化为含2个Ti原子的晶胞来处理。由表2可见,几何优化得到的β-Ti平衡晶格常数为a=0.328 18 nm,与外推得到的20 ℃时的晶格常数值一致。几何优化得到的H原子位于四面体间隙的β-Ti-H晶体的平衡结构仍为体心立方结构,平衡晶格常数a、b和c均大于β-Ti的平衡晶格常数。位于四面体间隙的H原子使β-Ti晶体体积膨胀,并随着氢含量的增加,体积膨胀率增大,Ti与H摩尔比为2?1的β-Ti-H晶体的体积膨胀率高达4.20%。几何优化得到的H原子位于八面体间隙的β-Ti-H-晶体的平衡晶体结构和晶格常数与β-Ti晶体相比均发生改变。晶体结构转变为体心四方结构(bct),平衡晶格常数a和b减小,而c增大。并随着氢含量的增加,a和b减小的幅度和c增大的幅度均变大。位于八面体间隙的H原子使β-Ti晶体体积膨胀,但膨胀率比H位于四面体间隙时的小。
表2 β-Ti和β-Ti-H晶体的晶格常数和晶体结构的计算结果
Table 2 Calculated results of lattice constants and crystal structures of β-Ti and β-Ti-H crystals

根据晶体结构理论,在体心立方结构晶体中,四面体间隙大于八面体间隙。如β-Ti晶体的八面体间隙rx(晶体中间隙大小的度量,也称间隙半径)为0.027 78 nm,四面体间隙rx为0.042 78 nm,因而,间隙原子应占据四面体间隙位置。但另一方面,由于体心立方结构晶体的八面体间隙是不对称的,即使间隙原子占据八面体间隙位置,也只引起距间隙中心a/2的两个原子显著偏离平衡位置,其余4个原子则不会显著地偏离平衡位置,因而,总的点阵畸变不大。因此,在体心立方金属中,间隙原子既可能占据四面体间隙位置(如碳在钼中),也可能占据八面体间隙位置(如碳在α铁中)。比较本研究几何优化得到的H位于不同间隙位置的β-Ti-H晶体的平衡晶格常数和晶体结构可见,H原子占据八面体间隙引起距间隙中心a/2的两个Ti原子显著偏离平衡位置,导致c增大;而其余4个Ti原子则向间隙中心偏移,引起晶格沿a和b轴方向收缩,因而晶体总的点阵畸变不大,晶体体积膨胀较小,这与上述理论相符。此外,氢含量越高,位于八面体间隙的氢原子引起晶格沿a和b轴方向收缩越大,因而,随着氢含量的增加,晶体的体积膨胀率反而减小。而H原子占据四面体间隙则使β-Ti晶体点阵产生较大畸变,晶体体积膨胀率明显比H原子占据八面体间隙时的高。单纯从晶格畸变程度的角度来考虑,根据计算结果,氢原子在β-Ti晶体中最可能的占位为八面体间隙位置,但还不能由此断言在β-Ti晶体中间隙H原子必定位于八面体间隙。由于除了畸变能外,氢原子与金属原子之间可能会形成一定的化学键使体系的能量降低,两种能量竞争的结果决定氢原子在金属中的占位[16-17],因此,氢原子在β-Ti晶体中的占位仍需要结合晶体能量进行进一步分析。
2.2 晶体结合能
晶体的结合能可以用来表征晶体的键合强度,比较晶体结合力。晶体结合能定义为

为了计算α-Ti-H和β-Ti-H晶体的结合能,本文作者首先计算了自由Ti原子和H原子的能量,分别为-1 601.012 eV和-13.310 eV。α-Ti和α-Ti-H晶体的总能量和结合能计算结果如表3所列。由表3可见,计算得到的α-Ti晶体的结合能(5.256 3 eV/atom)略大于实测结果(4.84 eV/atom)[18]。计算得到的不同Ti与H摩尔比的α-Ti-H晶体的结合能均小于α-Ti晶体的结合能,且随着氢含量的增加而减少。β-Ti和β-Ti-H晶体的结合能计算结果如表4所列。β-Ti晶体结合能为5.148 0 eV/atom,略大于实测值(4.77 eV/atom)[18]。氢原子位于不同间隙位置的β-Ti-H晶体的结合能均小于β-Ti晶体的结合能,且随着氢含量的增加而减少。根据TROIANO[19]提出的弱键理论(Decohesion Theory),当氢溶入过渡族元素后,由于过渡族元素的3d电子层未填满,氢原子的电子即进入金属的3d电子层,因而增加了d层电子的浓度,增加了原子间的排斥力,即降低了晶格的结合能。本研究的计算结果表明,氢降低了α-Ti和β-Ti晶体平均到单个原子的结合能,与氢致弱键理论相符。
2.3 氢在钛晶体中的溶解热
钛及钛合金的渗氢过程就是氢在钛及钛合金中的溶解扩散过程。吸附在钛表面的氢气分子首先分解成氢原子,氢原子通过扩散进入钛晶体内成为固溶氢原子。氢由气态到固溶态时的能量变化即为氢在Ti晶体中的溶解热,由于氢溶解在钛中属放热反应,故氢在钛晶体中的溶解热为负值,可由下式计算:

利用氢在钛晶体中的溶解热可以对钛-氢体系相结构的稳定性进行估计和预测,即氢在钛中的溶解热绝对值越大,则相结构越稳定。
本文计算得到的自由氢分子的能量为-31.642 41 eV,根据式(2)计算得到的氢在α-Ti和β-Ti晶体中的溶解热分别见表3和4。由表3可见,氢在钛-氢摩尔比为32?1和16?1的α-Ti-H超晶胞中的溶解热基本相同,约为-0.59~-0.58 eV。而在钛-氢摩尔比为8?1的α-Ti-H超晶胞中,氢的溶解热的绝对值比前两者小,表明Ti与H摩尔比为8?1的α-Ti-H晶体结构的稳定性比前两者差,这与前面晶体结构优化分析结果一致。
表3 α-Ti和α-Ti-H晶体的能量计算结果
Table 3 Calculated energies of α-Ti and α-Ti-H crystals
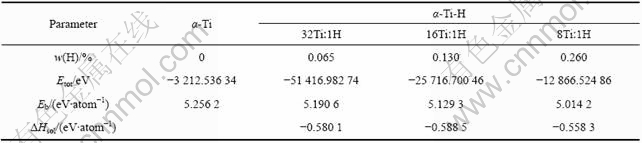
表4 β-Ti和β-Ti-H晶体的能量计算结果
Table 4 Calculated energies of β-Ti and β-Ti-H crystals
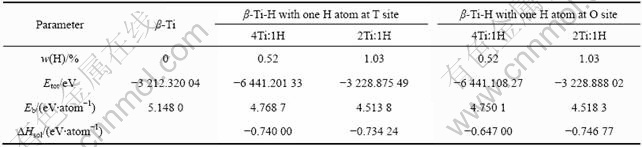
比较表4中各β-Ti-H晶体中氢的溶解热计算结果可知,在Ti与H摩尔比为4?1的β-Ti-H晶体中,H原子位于四面体间隙时的溶解热的绝对值比位于八面体间隙时高约0.1 eV;而在Ti与H摩尔比为2?1的β-Ti-H晶体中,H原子位于八面体间隙的溶解热的绝对值比位于四面体间隙时高约0.01 eV。由本研究的计算结果可知,若单纯根据氢在β-Ti晶体中溶解热来确定氢原子的占位,则在Ti与H摩尔比为4?1的β-Ti-H晶体中,H原子应占据四面体间隙位置,而在Ti与H摩尔比为2?1的β-Ti-H晶体中,H原子倾向于占据八面体间隙位置。
从晶格畸变程度和能量的角度综合分析,认为H原子在β-Ti-H晶体中的占位可能是不固定的,且随着氢含量变化。当氢含量较低时(如Ti与H的摩尔比为4?1),氢原子占据β-Ti晶体的四面体间隙时,其溶解热绝对值比氢在八面体间隙时要高得多,而晶格畸变程度仅比在八面体间隙时略大(体积膨胀率分别为1.21%和0.81%)。此时,氢原子的占位应主要由溶解热决定,因此,氢原子易于占据四面体间隙位置;当氢含量较高时(如Ti与H摩尔比为2?1),氢原子占据β-Ti晶体的八面体间隙时,其溶解热绝对值比在四面体间隙的稍高,而晶格畸变程度比在四面体间隙小很多(体积膨胀率分别为0.58%和4.2%),因此,氢原子更倾向于占据八面体间隙位置。
3 结论
1) 位于间隙位置的氢原子引起α-Ti和β-Ti晶格点阵发生畸变,晶体体积膨胀。钛晶体中的氢含量越高,晶格畸变程度越高,晶体体积膨胀越大。
2) 计算得到的不同钛与氢摩尔比的α-Ti-H和β-Ti-H晶体结合能分别小于α-Ti和β-Ti晶体结合能,表明氢原子降低了α-Ti和β-Ti晶体的结合能。
3) H原子在β-Ti-H晶体中的占位随着氢含量的变化而变化。当氢含量较低时(如Ti与H摩尔比为4?1),氢易于占据四面体间隙位置,而氢含量较高时(如Ti与H摩尔比为2?1),氢原子倾向于占据八面体间隙位置。
REFERENCES
[1] ELIAS R J, CORSO H L, GERVASONI J L. Fundamental aspects of the Ti-H system: theoretical and experimental behaviour[J]. International Journal of Hydrogen Energy, 2002, 27(1): 91-97.
[2] SHIH D S, ROBERTSON I M. Hydrogen embrittlement of alpha titanium[J]. Acta Metall, 1988, 36(1): 111-124.
[3] BRIANT C L, WANG Z F, CHOLLOCOOP N. Hydrogen embrittlement of commercial purity titanium[J]. Corrosion Science, 2002, 44(8): 1875-1888.
[4] 曹建玲, 沈保罗, 高升吉. Ti-Al-Zr合金的氢致延迟断裂行为[J]. 中国有色金属学报, 2002, 12(S1): 74-77.
CAO Jian-ling, SHEN Bao-luo, GAO Sheng-ji. Hydrogen induced delayed fracture behavior of Ti-Al-Zr alloy[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(S1): 74-77.
[5] SENKOV O N, FROES F H. Thermohydrogen processing of titanium alloys[J]. International Journal of Hydrogen Energy, 1999, 24(6): 565-576.
[6] ILYIN A A, SKVORTSOVA S V, MAMONOV A M, PERMYAKOVA G V, KUMIKOV D A. Effect of thermohydrogen treatment on the structure and properties of titanium alloy castings[J]. Met Sci Heat Treat, 2002, 44(5/6): 185-189.
[7] YOSHIMURA H, NAKAHIGASHI J. Ultra-fine-grain refinement and superplasticity of titanium alloys obtained through protium treatment[J]. International Journal of Hydrogen Energy, 2002, 27(7/8): 769-774.
[8] MURZINOVA M A, SALISHCHEV G A, AFONICHEV D D. Formation of nanocrystalline structure in two-phase titanium alloy by combination of thermohydrogen processing with hot working[J]. International Journal of Hydrogen Energy, 2002, 27(7/8): 775-782.
[9] 侯红亮, 李志强, 王亚军, 关 桥. 钛合金热氢处理技术及其应用前景[J]. 中国有色金属学报, 2003, 13(3): 533-549.
HOU Hong-liang, LI Zhi-qiang, WANG Ya-jun, GUAN Qiao. Technology of hydrogen treatment for titanium alloy and its application prospect[J]. The Chinese Journal of Nonferrous Metals, 2003, 13(3): 533-549.
[10] ZONG Y Y, SHAN D B, L? Y, GUO B. Effect of 0.3 wt%H addition on the high temperature deformation behaviors of Ti-6Al-4V Alloy[J]. International Journal of Hydrogen Energy, 2007, 32(16): 3936-3940.
[11] CHEN Y X, WAN X J, LI F, WANG Q J, LIU Y J. The behavior of hydrogen in high temperature titanium alloy Ti-60[J]. Mat Sci Eng A, 2007, 466(1/2): 156-159.
[12] KERR W R. The effect of hydrogen as a temporary alloying element on microstructure and tensile properties of Ti-6Al-4V[J]. Metall Trans A, 1981, 16A: 1077-1087.
[13] SENKOV O N, DUBOIS M, JONAS J J. Elastic module of titanium-hydrogen alloys in the temperature range 20 ℃ to 1 100 ℃[J]. Metallurgical and Materials Transactions A, 1996, 27(12): 3963-3970.
[14] SONG Y, GUO Z X, YANG R. Influence of interstitial elements on the bulk modulus and theoretical strength of α-titanium: a first-principles study[J]. Philosophical Magazine A, 2002, 82(7): 1345-1359.
[15] SEGALL M D, LINDAN P, PROBERT M J. First-principles simulation: ideas, illustrations and the CASTEP code[J]. J Phys: Condens Matter, 2002, 14(11): 2717-2744.
[16] HEMPELMANN R, RICHTER D, STRITZKER B. Optic phonon modes and super-conductivity in α phase (Ti, Zr)-(H, D) alloy[J]. J Phys F, 1982, 12(1): 79-82.
[17] PANIN A V, RYBIN V V, USHKOV S S, KAZACHENOK M S. Effect of hydrogen treatment on mechanical behavior of titanium with various structural states[J]. Physical Mesomechanics, 2003, 6(1): 17-24.
[18] KING H W. Crystal structures of the elements at 25[J]. Bullitin of Alloy Diagram, 1981, 2(4): 402-407.
[19] TROIANO A R. The role of hydrogen and other interstitial in the mechanical behavior of metals[J]. Trans ASM, 1960, 52(1): 54-80.
基金项目:国家自然科学基金资助项目(50671028)
收稿日期:2007-06-06;修订日期:2007-11-29
通讯作者:孙东立,教授,博士;电话:0451-86418635;E-mail: sundl1958@hit.edu.cn
(编辑 李艳红)