舰船周围铁磁物体对其磁场的影响

姚振宁，刘大明，朱兴乐

(海军工程大学 电气与信息工程学院，湖北 武汉，430033)

摘要：舰船与周围铁磁物体相互磁化产生附加的感应磁场，影响舰船磁场的磁感应强度的测量，针对此问题提出一种求解附加感应磁场的磁感应强度的计算方法。该方法以舰船与铁磁物体的磁偶极子阵列作为磁场数学模型，以系数矩阵条件数为目标函数的蚁群算法来优化磁偶极子的分布位置，并把物体的磁化等效为其磁模型中各磁偶极子的磁化，借助于均匀地磁场对舰船、铁磁物体磁化产生的感应磁场的磁感应强度来求解出各自的附加感应磁场强度，最终得到舰船磁场的磁感应强度。实验结果表明：该计算方法可行，且计算精度较高。

关键词：舰船磁场；附加感应磁场；磁感应强度；磁模型；磁偶极子

中图分类号：TM153.1             文献标志码：A         文章编号：1672-7207(2014)05-1491-05

Effect of ferromagnetic objects on magnetic field of vessel

YAO Zhenning, LIU Daming, ZHU Xingle

(College of Electrical and Information Engineering, Naval University of Engineering, Wuhan 430033, China)

Abstract: As additional induction field which is produced by magnetization between a vessel and ferromagnetic objects and affects magnetic measurement, a calculating method for additional induction field intensity was proposed. Magnetic dipole array model for a vessel and ferromagnetic objects was gotten, and ant colony algorithm whose objective function is condition number of the coefficient matrix was used to optimize the location of magnetic dipoles. Based on the assumption that an object’s magnetization is equivalent to each magnetic dipole’s magnetization in magnetic model, additional induction field and the vessel’s magnetic field intensity were worked out by recurring to the vessel’s and ferromagnetic object’s magnetization in symmetrical geomagnetic field. The results of a model experiment show that the method is feasible and has high accuracy.

Key words: vessel’s magnetic field; additional induction field; magnetic induction; magnetic model; magnetic dipole

在舰船磁性防护领域，通过测量舰船周围空间磁场的磁感应强度，检测舰船磁性状态以及评估舰船磁性防护水平。对于钢铁建造成的舰船，若周围没有其他铁磁物体，则其空间磁场只由舰船的固定磁场和被地磁场磁化产生的感应磁场组成。若舰船周围存在如拖船、铁磁设备等铁磁物体且距离较近，则舰船与这些铁磁物体相互磁化，产生附加的感应磁场，因而舰船周围空间磁场的磁感应强度测量值并不等于舰船磁场与铁磁物体磁场的磁感应强度的叠加。由于附加感应磁场的存在，空间磁场的磁感应强度测量值不能如实反映舰船磁性，如何由空间磁场的磁感应强度测量值计算舰船磁场的磁感应强度成为舰船磁防护工作中可能碰到的技术难题，解决这个问题必须求出附加感应磁场的磁感应强度。目前，许多文献通过有限元法或积分方程法对磁性物体的感应磁场的磁感应强度计算进行了大量研究^[1-7]，这2种方法需要对物体或场域进行剖分，剖分一般较复杂，且剖分的疏密程度直接影响计算精度。另外，这些研究大多是计算地磁场磁化产生的感应磁场的磁感应强度，由物体间相互磁化产生的附加感应磁场的磁感应强度计算研究却很少。为此，本文作者考虑附加感应磁场的影响，建立磁模型，再把物体的磁化等效为其磁模型中各磁偶极子的磁化，给出一种求解附加感应磁场的磁感应强度的计算方法。

1  基于磁体模拟法的磁场数学模型

舰船与铁磁物体形状不规则、磁化不均匀，难以用解析法求解其磁场的磁感应强度。一般采用磁体模拟法建立磁模型，即用若干个具有特定磁矩的磁性模拟体(磁偶极子、旋转椭球体)所产生的磁场模拟不规则物体的磁场，然后由磁性模拟体计算场域空间的磁场的磁感应强度^[8]。这里采用磁偶极子阵列进行建模。

假设磁偶极子数为n，舰船在第j个测量点产生磁场三分量为h_xj，h_yj和h_zj，则有方程组：

      (1)

式中：m_xi，m_yi和m_zi分别为第i个磁偶极子沿x，y和z轴方向的磁矩分量；f_xji，f_yji，f_zji，g_xji，g_yji，g_zji，e_xji，e_yji和e_zji为与测量点坐标、磁偶极子位置有关的常数，由它们组成了方程组的系数矩阵。在实际舰船磁场的磁感应强度测量中，在舰船下方某个平面测量磁场的磁感应强度，根据式(1)组成矛盾方程组，求其最小二乘解可得各个磁偶极子的磁矩，进而可求场域空间磁场的磁感应强度，即建立了磁模型。

磁偶极子原则上可以布设在所模拟物体区域的任何位置，为了简便，一般布设在水线面上。为了提高模型精度，一般将磁偶极子个数取得较多，但太多的磁偶极子使系数矩阵列相关性增强，其条件数变得非常大，以上方程组将呈现病态，因而模型不再稳定。系数矩阵条件数与磁偶极子位置有关，为了建立稳定的磁模型，可以利用智能优化算法来确定磁偶极子的分布位置^[9-11]。

本文以系数矩阵条件数作为目标函数，利用改进的蚁群算法-蚁群系统^[12-14]对磁偶极子位置进行优化，如图1所示，考虑实际舰船与吃水线相交情况，把舰船水线面形状近似看作椭圆，假设其磁偶极子个数为M, 将水线面沿长度方向也分成M等分，则第i个磁偶极子在阴影范围内优化取值(i=1, 2, …, M)。对于舰船周围铁磁物体，其磁偶极子位置的优化按照此方法进行。

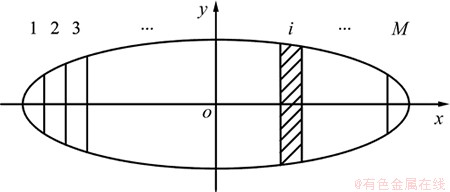
图1  磁偶极子位置的优化

Fig. 1  Magnetic dipoles’ optimization

2  周围有铁磁物体存在时的舰船磁场的磁感应强度计算

2.1  基本思想

当舰船周围有铁磁物体存在时，它们之间相互磁化产生各自的附加感应磁场。在实际的舰船磁场的磁感应强度测量中，如果只能测得其下方某一测量面上总磁场的磁感应强度h与铁磁物体磁场的磁感应强度h₂，假设舰船磁场磁感应强度为h₁，则有

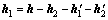              (2)

式中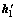：为舰船的附加感应磁场的磁感应强度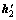；为铁磁物体的附加感应磁场的磁感应强度。可见，由于舰船与铁磁物体相互磁化产生了附加感应磁场，总磁场的磁感应强度与铁磁物体磁场的磁感应强度之差并不等于真实的舰船磁场的磁感应强度。

由式(2)可知，要得到真实的舰船磁场的磁感应强度必须计算出附加感应磁场的磁感应强度。一个物体的附加感应磁场是由另一物体对其磁化产生的，这种磁化是非均匀磁场对非规则物体的非均匀磁化，无法直接用解析式进行磁场的磁感应强度计算，所以必须等效为对规则物体的均匀磁化。结合磁模型，不妨认为对物体的磁化等效为对其磁模型中各磁偶极子的磁化，这样就可以直接用解析法计算磁场的磁感应强度。

2.2  附加感应磁场的磁感应强度的计算

设舰船磁模型中磁偶极子的三分量磁矩为m_xj，m_yj，m_zj(用M个磁偶极子模拟，j=1, 2, …, M)，设铁磁物体磁模型中磁偶极子的三分量磁矩为m_xj，m_yj，m_zj(用N-M个磁偶极子模拟，j=M+1, M+2, …, N)，则铁磁物体对舰船的第i个磁偶极子产生的附加磁化场三分量为(i=1, 2, …, M)

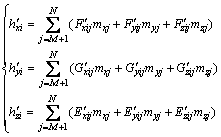      (3)

舰船对铁磁物体的第i个磁偶极子产生的附加磁化场三分量为(i=M+1, M+2, …, N)

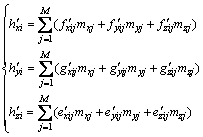       (4)

舰船、铁磁物体的第i个磁偶极子的附加感应磁矩三分量为(i=1, 2, …, N)

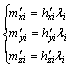                 (5)

式中：λ_i为第i个磁偶极子的附加感应磁矩与其附加磁化场之间所设的比例常数。式(4)中舰船磁偶极子的磁矩由h-h₂根据式(1)近似求出，式(3)中铁磁物体磁偶极子的磁矩由h₂根据式(1)求出。

比例常数λ_i可借助于均匀地磁场对舰船、铁磁物体的磁化而求出，即

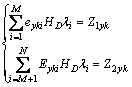            (6)

式中：H_D为地磁场的磁感应强度水平分量；Z_1yk和Z_2yk分别为舰船、铁磁物体在第k个测量点由H_D横向磁化产生的感应磁场的磁感应强度垂直分量，一般通过测量计算求出，作为已知数据。将Z_1yk和Z_2yk代入式(6)即可组成关于λ_i的矛盾方程组，求其最小二乘解可得λ_i。

根据式(3)~(6)可得附加感应磁矩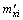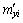，和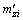，进而可得附加感应磁场的磁感应强度为

    (7)

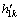式中：和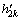分别为舰船、铁磁物体在第k个测量点的附加感应磁场。求出附加感应磁场强度后，由式(2)可求得舰船磁场磁感应强度。

3  计算实例

为了检验上述舰船磁场计算方法的可行性，利用磁场的磁感应强度测量值进行计算验证。实验磁场模型如图2所示。铁质的舰船模型长4.8 m、最大宽度0.54 m，其水线面近似为椭圆形，铁磁物体为1个长2.1 m、半径0.2 m的铁质空心圆筒，其水线面为长方形，坐标原点取船模水线面中心。在下方测量平面放置高精度的磁通门传感器阵列(对应船模左舷外、左舷、龙骨、右舷、右舷外正下方5条测量线，每条测量线31个测量点)，传感器纵向间距0.24 m、横向间距0.27 m。首先，测量船模与圆筒在一起的总磁场的磁感应强度以及船模不存在时的圆筒磁场的磁感应强度，然后，根据上述算法计算船模磁场的磁感应强度；最后，测量船模磁场的磁感应强度，将其测量值与计算值进行比较。

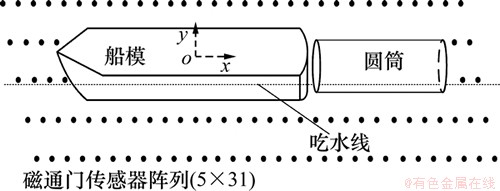
图2  实验磁场模型示意图

Fig. 2  Sketch map of experimental magnetic model

取磁偶极子所在水线面宽度为实际的1/4。用30个磁偶极子模拟船模磁场，用15个磁偶极子模拟圆筒磁场，则磁偶极子通过蚁群算法优化后的分布位置如图3所示。

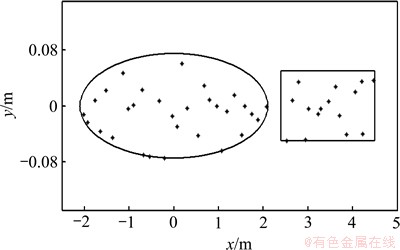
图3  磁偶极子分布位置

Fig. 3  Distribution of magnetic dipoles

在实际的舰船磁性检测站，通常只分析研究舰船磁场的磁感应强度的垂直分量。图4所示为船模磁场的磁感应强度垂直分量在左舷、龙骨、右舷下方的测量值与2种计算值的对比，其中直接计算值由总磁场的磁感应强度直接减去圆筒磁场的磁感应强度求出，且磁感应强度已经过归一化处理。由图4可见：算法计算值与测量值吻合较好，相对均方差为2.0%，最大相对误差为5.4%，说明该计算方法能够有效地计算有其他铁磁物体干扰时的舰船磁场的磁感应强度；而不考虑附加感应磁场的磁感应强度的直接计算值在(1,3)区段误差较大，相对均方差为5.2%，最大相对误差为13.4%，这是因为船模与圆筒接触区域的相互磁化比较严重，在其正下方(1,3)区段产生的附加感应磁场的磁感应强度较大。

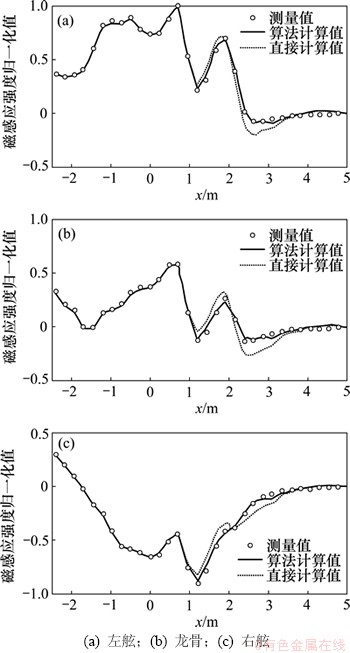
图4  船模磁场测量值与计算值对比

Fig. 4  Comparisons between calculated magnetic field and measured one

从上述计算过程来看，该计算方法也存在一定误差：磁偶极子的附加磁化场是由下方测量面磁场的磁感应强度换算得到，且磁场的磁感应强度测量数据有限，这属于远场到近场的换算问题^[15-16]，磁偶极子的附加磁化场存在误差；另外，该算法把物体的磁化近似等效为其磁模型中各磁偶极子的磁化，没有考虑磁偶极子之间相互干扰，导致磁偶极子的附加感应磁矩与其附加磁化场之间的比例常数λ_i存在误差。但是，由计算结果可知：以上2种误差并不大，总的来说本文所提算法是有效可行的。

4  结论

(1) 提出了一种舰船与铁磁物体在一起时的舰船磁场计算方法。

(2) 该算法首先分别建立舰船与铁磁物体的磁模型，并利用蚁群算法优化磁偶极子的分布位置，然后把物体的磁化等效为其磁模型中各磁偶极子的磁化，求出附加感应磁场的磁感应强度，进而得出真实的舰船磁场的磁感应强度。测试结果表明该计算方法可行。

参考文献：

[1] Bartusek K, Fiala P, Mikulka J. Numerical modeling of magnetic field deformation as related to susceptibility measured with an MR system[J]. Radioengineering, 2008, 17(4): 113-118.

[2] Nguyen T S, Guichon J M, Chadebec O, et al. Ships magnetic anomaly computation with integral equation and fast multipole method[J]. IEEE Transactions on Magnetics, 2011, 47(5): 1414-1417.

[3] 郭成豹, 张晓锋, 肖昌汉, 等. 地磁场中空心铁磁圆柱体纵向磁化状态数值分析[J]. 哈尔滨工程大学学报, 2006, 27(6): 886-890.

GUO Chengbao, ZHANG Xiaofeng, XIAO Changhan, et al. The numerical simulation of the longitudinal magnetic state of a hollow ferromagnetic cylinder in the geomagnetic field[J]. Journal of Harbin Engineering University, 2006, 27(6): 886-890.

[4] 周国华, 肖昌汉, 闫辉, 等. 一种弱磁作用下铁磁物体感应磁场的计算方法[J]. 哈尔滨工程大学学报, 2009, 30(1): 91-95.

ZHOU Guohua, XIAO Changhan, YAN Hui, et al. A method to calculate the induced magnetic field of ferromagnetic objects in a weak magnetic field[J]. Journal of Harbin Engineering University, 2009, 30(1): 91-95.

[5] Le Dorze F, Bongiraud J P. Modeling of degaussing coils effects in ships by the method of reduced scalar potential jump[J]. IEEE Transactions on Magnetics, 1998, 34(5): 2477-2480.

[6] Pechenkov A N. A mathematical algorithm for solving the inverse problem of magnetostatic flaw detection[J]. Russian Journal of Nondestructive Testing, 2005, 41(11): 714-718.

[7] Pechenkov A N. Numerical simulation of an inverse problem of magnetostatic flaw detection[J]. Russian Journal of Nondestructive Testing, 2005, 41(11): 719-723.

[8] 周耀忠, 张国友. 舰船磁场分析计算[M]. 北京: 国防工业出版社, 2004: 135-136.

ZHOU Yaozhong, ZHANG Guoyou. Analysis and computing of marine vessels’ magnetic field[M]. Beijing: National Defense Industry Press, 2004: 135-136.

[9] 刘胜道, 刘大明, 肖昌汉, 等. 基于遗传算法的磁性目标磁模型[J]. 武汉理工大学学报, 2008, 32(6): 1017-1020.

LIU Shengdao, LIU Daming, XIAO Changhan, et al. Magnetic model for magnetic objects based on genetic algorithm[J]. Journal of Wuhan University of Technology, 2008, 32(6): 1017-1020.

[10] 徐杰, 刘大明, 周国华, 等. 一种基于遗传优化算法的潜艇高空磁场换算方法[J]. 舰船科学技术, 2009, 31(1): 156-159.

XU Jie, LIU Daming, ZHOU Guohua, et al. Application of genetic algorithm in continuation of magnetic field of submarines in high areas[J]. Ship Science and Technology, 2009, 31(1): 156-159.

[11] 张朝阳, 肖昌汉, 徐杰. 基于微粒群优化算法的舰船磁模型分析[J]. 华中科技大学学报, 2010, 38(11): 124-128.

ZHANG Zhaoyang, XIAO Changhan, XU Jie. Analysis of magnetic model for ships using particle swarm optimization method[J]. Journal of Huazhong University of Science and Technology, 2010, 38(11): 124-128.

[12] Dorigo M, Gambardella L M. Ant colony system: A cooperative learning approach to the traveling salesman problem[J]. IEEE Trans on Evolutionary Computation, 1997, 1(1): 53-56.

[13] Dorigo M, Caro G D, Gambardella L M. Ant algorithms for discrete optimization[J]. Artificial Life, 1999, 5(2): 137-172.

[14] 付宇. 蚁群优化算法的改进及应用[D]. 上海: 上海海事大学物流工程学院, 2006: 20-22.

FU Yu. The improvement and application of ant colony optimization[D]. Shanghai: Shanghai Maritime University. College of Logistics Engineering, 2006: 20-22.

[15] 徐世浙. 地球物理中的边界单元法[M]. 北京: 科学出版社, 1995: 40-75.

XU Shizhe. BEM in geophysics[M]. Beijing: Science Press, 1995: 40-75.

[16] 闫辉, 肖昌汉, 殷克全, 等. 递推算法在船舶磁场远场向近场换算中的应用[J]. 兵工学报, 2010, 31(9): 1200-1203.

YAN Hui, XIAO Changhan, YIN Kequan, et al. The application of recursive algorithm on ship’s magnetic field extrapolation[J]. Acta Armamentarii, 2010, 31(9): 1200-1203.

(编辑  赵俊)

收稿日期：2013-05-06；修回日期：2013-08-28

基金项目：国家自然科学基金资助项目(51277176)

通信作者：姚振宁(1987-)，男，河南商丘人，博士研究生，从事舰船磁场测量与计算研究；电话：18986067954；E-mail: yaozhenning1987@163.com