基于Bishop法假定的边坡临界滑动场方法及应用

李亮¹，杨小礼²，禇雪松¹，于广明¹，路世豹¹

(1. 青岛理工大学 土木工程学院，山东 青岛，266033；

2. 中南大学 土木工程学院，湖南 长沙，410075)

摘要：针对边坡临界滑动场方法一般选取剩余力作为控制指标的局限，基于简化Bishop法假定，在给定安全系数下，对圆弧滑动面和非圆弧滑动面分别选用剩余力矩(滑动力矩与抗滑力矩之差)和剩余法向力力作为控制指标，从众多的可行滑动面中选择控制指标最大的那个滑动面作为给定安全系数下的危险滑动面，不断变化安全系数直至找到控制指标最大值等于零的危险滑动面作为边坡临界滑动面，形成基于Bishop法假定的边坡临界滑动场方法。将该新方法应用于2个典型土坡的稳定性分析中，通过比较分析证明该方法与常规的Bishop法得到了一致的结果。

关键词：岩土工程；边坡稳定；临界滑动场方法；Bishop法；安全系数

中图分类号：TU441        文献标志码：A         文章编号：1672-7207(2011)09-2848-05

Critical slip field algorithm with Bishop method

assumption and its application

LI Liang¹, YANG Xiao-li², CHU Xue-song¹, YU Guang-ming¹, LU Shi-bao¹

 (1. School of Civil Engineering, Qingdao Technological University, Qingdao 266033, China;

2. School of Civil Engineering, Central South University, Changsha 410075, China)

Abstract: The control index of residual force is usually adopted in the general critical slip field method, in order to extend the critical slip field in terms of control index, the control index of residual moment which is defined as the difference between the sliding moment and anti-sliding moment for the circular slip surface and residual normal force at the exit point for the non-circular are used based on the Bishop method assumption at given factor of safety. The dangerous slip surface can be located from many potential slip surfaces having maximum value of control index at given factor of safety. The given factor of safety is altered to find critical slip surface which is the dangerous slip surface with zero maximum value of control index. This critical slip field algorithm with Bishop method is used to assess the stability of two typical slopes and the comparison to general Bishop method shows that this new algorithm is feasible and valid.

Key words: geotechnical engineering; slope stability analysis; critical slip field; Bishop method; factor of safety

边坡稳定的极限平衡条分法已历经五六十年甚至更长的发展时间，其在二维边坡稳定分析中的应用已日趋成熟与完善。目前水利水电工程边坡设计规范明确规定该法作为边坡稳定分析的基本与首要方法，对任意形状的滑动面，推荐采用摩根斯顿—普莱斯方法计算其安全系数，而对于圆弧滑动面，建议使用简化Bishop法^[1]计算相应的安全系数，对于圆弧滑动面，Bishop法的结果与摩根斯顿-普莱斯方法基本一致。朱大勇等^[2]对简化Bishop法的“严格”本质进行了论证，证明了简化Bishop法与摩根斯顿-普莱斯方法等“严格”方法是一致的。张鲁渝等^[3-4]针对简化Bishop法只能适用于圆弧滑动面进行了扩展，提出了扩展简化Bishop法，并对取矩中心的影响进行了详尽探讨。可以看出，简化Bishop法在极限平衡方法的应用与发展过程中起到了不可忽视的作用。对于给定滑动面，简化Bishop法需要进行简单迭代以求出其安全系数，对于荷载组合较简单的情况，不存在收敛性问题，但对于复杂何荷载以及地震力作用下，有可能出现收敛性问题。为此，本文作者将朱大勇等^[5-10]提出的基于剩余推力的临界滑动场方法扩展至剩余力矩范畴，通过算例比较分析证明了该方法的有效性。

1  基于Bishop法的剩余力矩与剩余法向力

1.1  剩余力矩

图1所示为简化Bishop法示意图。简化Bishop法仅考虑了垂直方向的力平衡条件与整体力矩平衡条件来确定安全系数，其相应的计算公式为：

       (1)

图1及式(1)中：W_i和Q_i分别为土条自重和水平方向外力；E_i和T_i分别为第i-1条块与第i条块之间的法向力和剪切力；E_i+1和T_i+1分别为第i条块与第i+1条块之间的法向力和剪切力；n为划分的条块数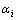；为土条底面的倾角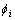；为土条底面上土体的摩擦角；C_i为土条底面上土体黏聚力之和；F_s为安全系数；N_i，S_i和U_i分别为条底的法向力和剪切力以及孔隙水压力。由式(1)可以发现F_s的求解需要经过迭代，变换式(1)得到剩余力矩M_r表达式：

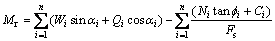  (2)

式(2)中给定安全系数F_s后，M_r很容易得到。本文在实际计算中发现，随着F_s的增大，M_r也随之增大，这与文献[5-10]中推力最大原理，“只要条间力方向与条块底面倾角组合在合理范围内，滑出端剩余推力始终随F_s增加而单调增加”类似。所以，类似地，也可推断出：只要条间力方向与条块底面倾角组合在合理范围内，基于Bishop法圆弧滑动面的剩余力矩始M_r终随F_s增加而单调增加。这样，在边坡问题中，M_r具有极大值，F_s最小化问题可转化为M_r最大化问题(约束条件为M_r=0)，也就是说，确定安全系数最小的临界滑动面等价于确定剩余力矩最大且为零的滑动面。

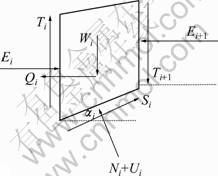
图1  简化Bishop法示意图

Fig.1  Illustration of simplified Bishop method

1.2  剩余法向力

对于非圆弧滑动面而言，取矩中心的选取对安全系数的影响不容忽视，文献[4]已经对该问题进行了探讨。为避开取矩中心的影响，本文采用滑出端的法向力E₁作为剩余法向力E_r，其计算公式为：

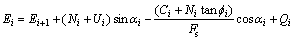  (3)

类似地，做如下推断：只要条间力方向与条块底面倾角组合在合理范围内，基于Bishop法非圆弧滑动面的滑出端剩余法向力E_r随F_s增加而单调增加。

2  基于Bishop法的边坡临界滑动场方法

同基于剩余推力的边坡临界滑动场方法类似，本文提出的基于Bishop法的临界滑动场方法共分2个计算步骤。

(1) 对于圆弧滑动面：

步骤1  首先假定安全系数F_s的初始值F₀ (可取1.0或者更小)。在假定安全系数F₀下，计算所有可行圆弧滑动面的M_r，从中选择M_r最大的圆弧滑动面作为F₀下，边坡的危险滑动面。

步骤2  逐步增大安全系数，假定一安全系数迭代增量?F_s (一般取一较小值如0.01)，在新的安全系数下去执行步骤1的操作，找到相应于新安全系数的危险滑动面。

步骤3  绘制安全系数与相应危险滑动面的剩余力矩M_r曲线，通过插值得到边坡最小安全系数和临界滑动面。

(2) 对于非圆弧滑动面：

步骤1  首先假定安全系数F_s的初始值F₀(可取1.0或者更小)。在假定安全系数F₀下，计算所有可行非圆弧滑动面的E_r，从中选择E_r最大的非圆弧滑动面作为F₀下，边坡的危险滑动面。

步骤2  逐步增大安全系数，假定一安全系数迭代增量?F_s(一般取一较小值如0.01)，在新的安全系数下去执行步骤1的操作，找到相应于新安全系数的危险滑动面。

步骤3  绘制安全系数与相应危险滑动面的剩余力矩E_r曲线，通过插值得到边坡最小安全系数和临界滑动面。

需要说明的是：在非圆弧滑动面的步骤1中，计算所有可行滑动面的剩余力矩或者剩余法向力的实现离不开优化算法，利用Geem等^[11]提出的和声算法进行危险滑动面的搜索。该法是一种简单有效的启发式算法，因参数少、易实现等优点已在许多领域成功应用。其基本原理及实现方法见文献[11]。此外，滑动面的构造方法采用少量点的直线连接来初步形成滑动面，然后采用样条函数细化的方法，该法具有减少优化变量个数的作用^[12]。文献[13]对其在模拟过程中的注意事项进行了探讨。

3  算例分析

3.1  均质土坡

拟采用2个算例来验证本文方法的有效性。首先给出一均匀土坡，坡角为45°，土的强度参数黏聚力c=40 kN/m²，内摩擦角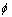=20°，容重γ=20 kN/m³。对于圆弧滑动面，采用剩余力矩与剩余法向力2个控制指标来模拟临界滑动场方法，其极大剩余力矩随安全系数的变化曲线见图2，其极大剩余法向力随安全系数的变化曲线见图3。由图2可以插值得到：极大剩余力矩等于零的安全系数为1.268，此即边坡最小安全系数。相应的临界滑动面见图4。由图3可以插值得出：边坡的最小安全系数为1.222，其临界滑动面也示于图4以便比较。

文献[14]给出了常见极限平衡条分法对该均匀土坡的计算结果，如表1所示。由表1可见：常规Bishop法的结果为1.266，本文基于剩余力矩控制指标的结果1.268与其基本一致，基于剩余法向力的结果1.222略小，与瑞典法结果接近。

图2  极大剩余力矩随安全系数的变化曲线

Fig.2  Variation curve of maximum residual moment with different values of factor of safety

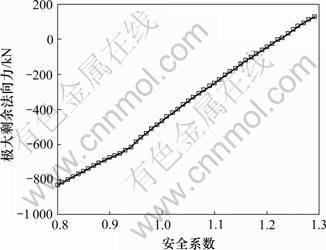
图3  极大剩余法向力随安全系数的迭代曲线

Fig.3  Variation curve of maximum residual normal force with different values of factor of safety

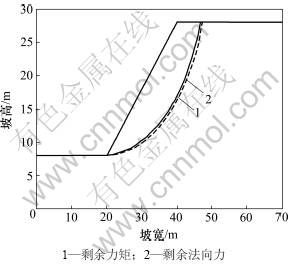
图4  临界滑动面比较

Fig.4  Different critical slip surfaces by different  control indexes

表1  均匀土坡的安全系数计算结果

Table 1  Results of factor of safety of homogeneous slope

3.2  非均质土坡

第2个土坡为非均质土坡，Zolfaghari等^[15]利用摩根斯顿-普莱斯方法来计算给定滑动面的安全系数，利用遗传算法来搜索最小安全系数，其结果为1.240。该土坡的剖面如图5所示，计算参数如表2   所示。

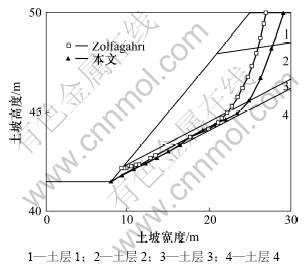
图5  非均质土坡的剖面及临界滑动面比较

Fig.5  Cross-section for on-homogeneous slope and critical slip surfaces

表2  Zolfaghari土坡计算参数

Table 2  Parameters of Zolfaghari slope

采用基于剩余法向力的边坡临界滑动场方法，非圆弧滑动面的计算结果见图6，从其剩余法向力随安全系数的迭代曲线可插值得到最小安全系数为1.116，与Zolfaghari等^[15]的结果1.240相差较大，本文的临界滑动面与Zolfaghari等^[15]的结果进行了对比(见图5)。将本文搜索得到的临界滑动面利用Slope2000重新计算(摩根斯顿-普莱斯法)得到安全系数为1.120，这说明Zolfaghari等^[15]采用的遗传算法有可能陷入局部最优值，没有发现最小的安全系数。从图5也可发现：本文滑动面较多部分位于软弱层内。该算例证明了本文基于剩余法向力的临界滑动场方法的有效性。

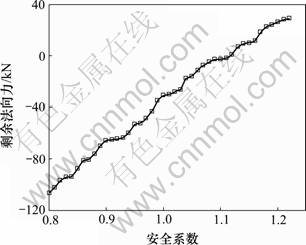
图6  极大剩余法向力随安全系数变化曲线

Fig.6  Variation curve of maximum residual normal force with different values of factor of safety

4  结论

(1) 基于简化Bishop法假定，针对圆弧滑动面和非圆弧滑动面，分别提出利用剩余力矩与剩余法向力2个控制指标来实现临界滑动场方法的扩展，通过在均质土坡和非均质土坡算例比较分析证明了本文方法的可行性。

(2) 对于圆弧滑动面，采用剩余力矩和剩余法向力2个控制指标得到的结果相差小于5%，临界滑动面位置基本一致；基于剩余力矩控制指标得到的安全系数与常规Bishop法得到的安全系数一致。

(3) 对于非圆弧滑动面，为避开取矩中心对计算的影响，最好采用剩余法向力控制指标进行。

参考文献：

[1] Bishop A W. The use of the slip circle in the stability analysis of slopes[J]. Geotechnique, 1955, 5(1): 7-17.

[2] 朱大勇, 邓建辉, 台佳佳. 简化Bishop法严格性的论证[J]. 岩石力学与工程学报, 2007, 26(3): 455-458.
ZHU Da-yong, DENG Jian-hui, TAI Jia-jia. Theoretical verification of rigorous nature of simplified bishop method[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 455-458.

[3] 张鲁渝, 郑颖人. 简化Bishop法的扩展及其在非圆弧滑面中的应用[J]. 岩土力学, 2004, 25(6): 927-929.
ZHANG Lu-yu, ZHENG Ying-ren. An extension of simplified Bishop method and its application to non-circular slip surface for slope stability analysis[J]. Rock and Soil Mechanics, 2004, 25(6): 927-929.

[4] 张鲁渝, 郑颖人. 扩展简化Bishop法的取矩中心对安全系数的影响[J]. 岩土力学, 2004, 25(8): 1239-1243.
ZHANG Lu-yu, ZHENG Ying-ren. Effect of moment axis on safety factors by extended simplified Bishop method[J]. Rock and Soil Mechanics, 2004, 25(8): 1239-1243.

[5] 朱大勇. 边坡临界滑动场及其数值模拟[J]. 岩土工程学报, 1997, 19(1): 63-69.
ZHU Da-yong. Critical slip field of slope and its numerical simulation[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(1): 63-69.

[6] 朱大勇, 姜弘道. 边坡临界滑动场方法与应用. Ⅰ: 理论基础[J]. 水利水电科技进展, 2000, 20(3): 63-66.
ZHU Da-yong, JIANG Hong-dao. Slope critical slip field method and its application. Ⅰ: Theoretical base[J]. Advances in Science and Technology of Water Resources, 2000, 20(3): 63-66.

[7] 朱大勇, 姜弘道. 边坡临界滑动场方法与应用. Ⅱ: 数值模拟[J]. 水利水电科技进展, 2000, 20(4): 65-68.
ZHU Da-yong, JIANG Hong-dao. Slope critical slip field method and its application. Ⅱ: Numerical simulation[J]. Advances in Science and Technology of Water Resources, 2000, 20(4): 65-68.

[8] 朱大勇, 姜弘道. 边坡临界滑动场方法与应用. Ⅲ: 工程应用[J]. 水利水电科技进展, 2000, 20(6): 64-67.
ZHU Da-yong, JIANG Hong-dao. Slope critical slip field method and its application. Ⅲ: Engineering application[J]. Advances in Science and Technology of Water Resources, 2000, 20(6): 64-67.

[9] 朱大勇, 周早生. 边坡全局临界滑动场(GCSF)理论及工程应用[J]. 土木工程学报, 1999, 32(3): 66-72.
ZHU Da-yong, ZHOU Zao-sheng. Theory of globally critical slip field of slopes and its application to practical engineering[J]. China Civil Engineering Journal, 1999, 32(3): 66-72.

[10] 朱大勇. 土体稳定性分析方法—临界滑动场方法[D]. 南京: 南京工程兵工程学院地下工程系, 1999: 48-89.
ZHU Da-yong. A method for soil stability analysis—CSF method[D]. Nanjing: Nanjing Engineering Institute. Department of Underground Engineering, 1999: 48-89.

[11] Geem Z W, Kim J H, Loganathan G V. Harmony search[J]. Simulation, 2001, 76(2): 60-68.

[12] Chen Z, Shao C. Evaluation of minimum factor of safety in slope stability analysis[J]. Canadian Geotechnical Journal, 1983, 25(4): 735-748.

[13] 李亮, 王秋生. 样条函数模拟土坡滑动面的效率分析[J]. 岩土工程技术, 2008, 22(3): 113-118.
LI Liang, WANG Qiu-sheng. Performance study on the generation of slip surface by spline function in the slope stability analysis[J]. Geotechnical Engineering Technique, 2008, 22(3): 113-118.

[14] 关立军. 基于强度折减的土坡稳定分析方法研究[D]. 大连: 大连理工大学土木水利学院, 2003: 55-60.
GUAN Li-jun. Research on the soil slope stability analysis method based on strength reduction method[D]. Dalian: Dalian University of Technology. School of Civil and Hydraulic Engineering, 2003: 55-60.

[15] Zolfaghari A R, Heath A C, McCombie P F. Simple genetic algorithm search for critical non-circular failure surface in slope stability analysis[J]. Computers and Geotechnics, 2005, 32(3): 139-152.

(编辑 杨幼平)

收稿日期：2010-08-23；修回日期：2010-11-29

基金项目：国家自然科学基金资助项目(51008167)；高等学校博士学科点专项科研基金资助项目(20103721120001)；山东省高等学校科技计划项目(J10LE07)

通信作者：李亮(1977-)，男，山东济南人，博士，副教授，从事道路边坡稳定分析研究；电话：0532-85071278；E-mail: liangli14@yahoo.com.cn