DOI：10.19476/j.ysxb.1004.0609.2017.04.022
采用密度泛函方法研究铜铅分离的抑制机理
张行荣，刘崇峻，朱阳戈，郑桂兵，尚衍波，韩 龙，艾 晶
(北京矿冶研究总院 矿物加工科学与技术国家重点实验室，北京 100160)
摘 要：为了从微观层面揭示巯基乙酸钠用于黄铜矿和方铅矿浮选分离的作用机理，从量子化学计算入手，利用密度泛函方法对黄铜矿与方铅矿晶体及表面电子结构进行研究。结果表明：黄铜矿与方铅矿表面原子的电子结构性质(如能带结构、态密度、Mulliken布居等)的差异是直接影响其可浮性的根本原因。根据前线轨道理论，从能量角度比较两种矿物与药剂之间的相互作用能，揭示巯基乙酸钠可用于铜铅浮选分离的实质。
关键词：密度泛函；黄铜矿；方铅矿；抑制剂；分离
文章编号：1004-0609(2017)-04-0843-07 中图分类号：TD923 文献标志码：A
铜铅金属广泛应用于汽车工业、国防、航天科技、建筑以及电子工业等各个领域，在国民经济建设中发挥着重要作用。铜铅锌多金属硫化矿作为提取铜铅的主要矿物，通常采用浮选的方法进行回收利用。但是铜铅锌多金属硫化矿往往致密共生，嵌布关系复杂，同时又由于铜矿物与铅矿物的可浮性相近，因此浮选时通常采用铜铅混选再分离工艺技术，但这也导致后续选别作业中铜铅分离的困难[1-3]。铜铅分离一直是国内外研究的难点和热点，传统的铜铅分离方法主要为氰化物抑铜法[4]和重铬酸盐抑铅法[5]，但是这两种方法或因溶解少量贵金或因产生严重的环境污染而逐渐被淘汰，为了适应新时代条件下的经济可持续发展及环保要求，人们逐渐发展了组合抑制剂和有机抑制剂[6]。有机抑制剂，如多糖类、纤维素类、栲胶等，由于来源广泛、低毒、价格低廉等优点得到了广泛应用而成为研究热点[7-8]。巯基乙酸钠在硫化矿浮选分离中是研究最多、生产应用较为成熟的一种有机抑制剂[9-10]，主要用作铜钼分离，国内外对巯基乙酸钠抑制黄铜矿的机理已有较多的研究[11]，而对铜铅分离的抑制机理尚且不多。密度泛函方法是近年来发展较为迅速的一种模拟计算方法，其在硫化矿浮选中的应用较为广泛和相对成熟。早在1993年，TOSSELL等[12]首次用从头算的方法研究了黄药、双黄药、金属离子黄药及相关化合物的分子轨道和电子结构，解释了它们的一些实验光谱差异；EDELBRO等[13]用密度泛函方法计算了黄铜矿的电子和能带结构，用理论计算结果讨论了矿物浮选特性和表面性质的关系。国内陈建华研究团队[14-17]利用第一性原理研究了黄铜矿、黄铁矿、方铅矿、闪锌矿等硫化矿的表面特性，指出硫化矿表面晶格缺陷是导致矿物可浮性差异的主要原因，并深入探讨了捕收剂分子、水分子等在硫化矿矿物表面的相互作用[18-20]。本研究的目的在于利用密度泛函理论研究铜铅矿物晶体电子结构性质，利用前线分子轨道理论分析巯基乙酸钠在铜铅分离中的作用机理，为将来新型铜铅分离抑制剂的研发提供理论参考。
1 计算模型及方法
根据文献[13-21]可知，黄铜矿晶格参数为a=b=5.24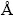 
，c=10.32 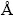，α=β=γ=90°；方铅矿晶格参数为a=b=c=5.93 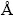。基于密度泛函理论(Density functional theory，DFT)，利用Materials Studio(MS)软件中Dmol3模块，采用广义梯度近似(Generalized gradient approximation，GGA)方法[23]对铜铅硫化矿晶体的电子结构性质进行模拟计算[22]，考察不同交换函数对其晶格参数的影响(见表1)。在计算电荷密度和体系总能量时，采用Monkhorst-pack (MP)方案对Brillouin Zone内的积分进行计算，其中黄铜矿采用3×3×1的k点网络，方铅矿采用2×2×2的k点网络。为保证体系的收敛性能，精度设为Fine，基组设为DNP 3.5，自洽收敛标准设为1.0×10-6 eV/atom，所有计算均采用了自旋极化。
表1 不同交换函数对黄铜矿和方铅矿晶格参数的影响
Table 1 Effects of functionals on crystal lattice parameters of CuFeS2 and PbS
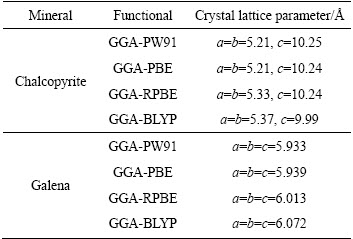
表1结果表明，对于黄铜矿和方铅矿两种硫化矿晶体，采用GGA-PW91(Perdew-Wang 1991)[24]修正函数计算出的晶格参数与实验值最为接近。因此，针对铜铅两种矿物在计算时选取的交换关联函数均为GGA-PW91。
2 结果与讨论
2.1 能带和态密度分析
黄铜矿和方铅矿晶体的能带结构及原子分态密度图如图1和2所示。
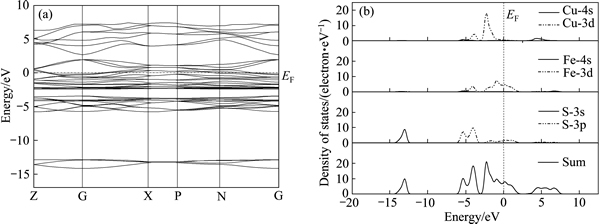
图1 黄铜矿的能带结构和各原子分态密度
Fig. 1 Band structure(a) and partial density of states (PDOS)(b) of chalcopyrite
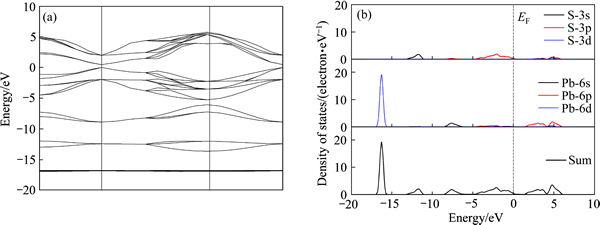
图2 方铅矿的能带结构和各原子分态密度
Fig. 2 Band structure(a) and partial density of states (PDOS)(b) of galena
由图1(a)可以看出：黄铜矿能带符合直接带隙p型半导体的特征，即价带极大值和导带极小值都位于高对称点G；模拟计算得到黄铜矿的禁带宽度为0.98 eV，与文献[25]中报道的非常接近。如图1(b)所示，黄铜矿的导带能级由Cu-4s轨道和Fe-4s轨道组成；而价带能级由两部分组成，其中-15.0~-12.4 eV的深部价带主要由S-3s轨道贡献，-6.4~2.5 eV的顶部价带由Cu-3d，Fe-3d和S-3p轨道组成，其中Cu-3d轨道成分最多，价带顶主要由Cu-3d轨道组成，导带底主要由Cu-4s和和S-3p轨道共同杂化组成，Cu-4s轨道贡献更大。
由图2(a)可看出，方铅矿也是一种直接带隙p型半导体；计算得到的方铅矿能隙为0.459 eV，与实验值0.410 eV相比稍有差距[26]，但这并不影响对其电子结构的分析。通过图2(b)可以看出，在费米能级附近，主要由S-3p轨道和Pb-6p轨道构成，其中S-3p贡献最大，因此理想方铅矿的天然可浮性较好。但当方铅矿暴露于空气中时，矿物表面会慢慢被氧化，使其可浮性变差，而经磨矿再处理后，方铅矿表面会形成新的解理面，疏水性能得以恢复。
矿物晶体内部离子、原子或分子可以相互结合，使得键能得到平衡，而裸露的矿物晶体表面常因键的断裂而具有与其内部结构不同的微观特性，如键的不饱和特性、原子的荷电情况等，正是因为这些微观的差异决定了其可浮性。
图3和4所示为黄铜矿和方铅矿解理面上各原子与晶体内部原子分态密度的对比图。通过图3可以看出，黄铜矿解理后，其(101)表面上的S、Fe、Cu原子分态密度与晶格内部原子相比，其分态密度均发生了较大的变化，这说明黄铜矿(101)表面的原子微观特性由于解理面的形成而产生了差异。在费米能级附近，(101)表面的Cu-3d和Fe-3d轨道贡献相对较大，以Cu-3d轨道贡献最多，这说明(101)表面Cu原子较Fe原子更为活泼。
由图4可看出，方铅矿沿(100)面解理后，由于键的断裂，表面原子分态密度也发生了变化。(100)表面S和Pb原子分态密度在费米能级附近分布有所增多，主要由S-3p轨道和Pb-6p轨道贡献，以S-3p轨道为多，所以，在(100)表面S原子和Pb原子都可以作为活性位点。
2.2 Mulliken布居分析
Mulliken布居是MULLIKEN等[27]在1955年提出的一种用于表示一体系中各组成原子的电荷分布与转移及各原子之间的成键性质的方法。根据键的Mulliken布居数大小，可以解释各原子之间的电荷转移及成键的强弱。键的Mulliken布居数越大，原子间成键的共价性越强；键的Mulliken布居数越小，成键的离子性越强。在同一基组条件下，黄铜矿与方铅矿的原子Mulliken布居数见表2，键的Mulliken布居数见表3。
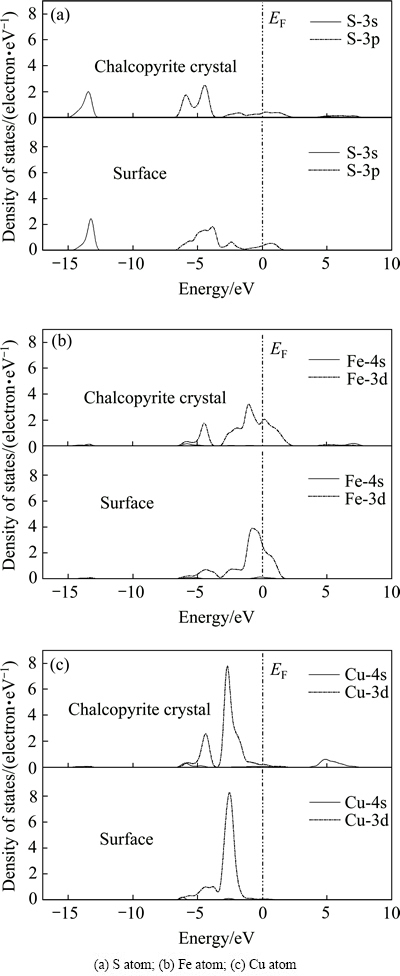
图3 黄铜矿(101)解理面上各原子的分态密度对比
Fig. 3 Comparison of PDOS of atoms on chalcopyrite (101) surface
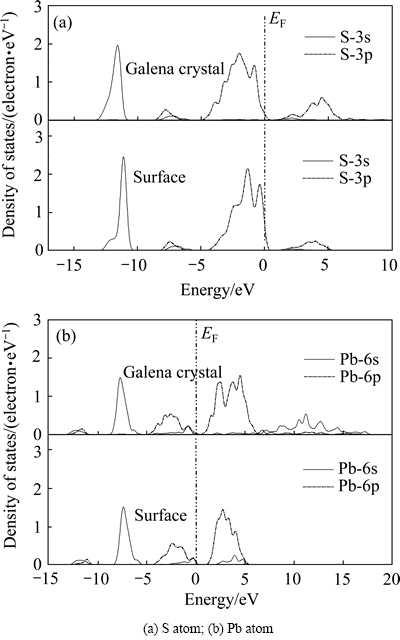
图4 方铅矿晶体与(100)表面原子分态密度比较
Fig. 4 Comparison of PDOS of atoms on galena (100) surface
表2 黄铜矿和方铅矿原子的Mulliken布居数
Table 2 Mulliken atomic population of chalcopyrite and galena
表3 黄铜矿和方铅矿原子间键的Mulliken布居数
Table 3 Mulliken bond population of chalcopyrite and galena
通过表2可以看出，优化后黄铜矿晶体中定域在S原子上的电子数为6.19，其中主要是p轨道得到电子，s轨道失去电子，电子共计得到0.19e，为电子受体；Fe原子上电子数为7.82，其中s轨道失去1.63e，d轨道得到0.91e，p轨道得到0.53e，共计失去0.19e；Cu原子上电子数为10.81，其中s轨道失去0.42e，d轨道失去0.27e，p轨道得到0.50e，共计失去0.19e。方铅矿经优化后，定域在S原子上的电子数为6.67，其中s轨道失去0.07e，p轨道得到0.74e，共计得到0.67e；Pb原子上的电子数为13.33，其中s轨道失去0.09e，p轨道失去0.58e，共计失去0.67e。表3所列为黄铜矿和方铅矿原子间键的Mulliken布居数，黄铜矿中S—Cu、S—Fe和方铅矿中S—Pb键的布居值分别为0.31、0.48、0.42，这说明在黄铜矿晶体中，S—Cu键较S—Fe键呈现出较强的离子性，因此在黄铜矿晶体中，Cu离子更具活泼性。而方铅矿中S—Pb键则主要更倾向于表现出共价键特性。
2.3 前线轨道理论分析
FUKUI等[28]提出的前线轨道理论认为分子的许多性质主要由分子中的前线轨道决定，即最高占据分子轨道(HOMO)和最低空轨道(LUMO)决定。该理论指出一个反应物的最高占据分子轨道(HOMO)与另一个反应物最低空轨道(LUMO)的能量之间的差值的绝对值(ΔE)越小越利于分子之间发生相互作用。把优化好的黄铜矿、方铅矿矿物晶体和巯基乙酸钠分子 (TGA)提交MS软件下的 Dmol3模块，从能量(Energy)角度对分子轨道性质进行模拟计算，模拟计算得到铜铅硫化矿物及TGA分子的前线轨道能量(见表4)。模拟计算时，关联函数选为GGA-PW91，收敛精度设为Fine，k-points选为Gamma，其他参数选择默认值。
表4 矿物和巯基乙酸钠前线轨道能量分析
Table 4 Frontier orbital energy of mineral and thioglycolic acid
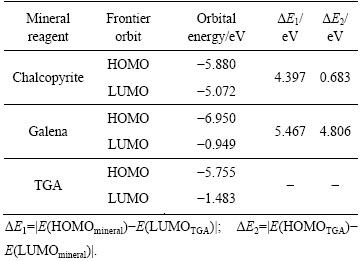
表4结果表明：药剂HOMO轨道与矿物LUMO轨道的能量差值绝对值(ΔE2)都小于矿物HOMO轨道与药剂LUMO轨道作用的能量差值绝对值(ΔE1)，根据福井谦一的前线轨道理论，药剂的HOMO轨道和矿物的LUMO轨道发生相互作用，这说明电子从TGA的HOMO轨道转移至矿物的LUMO轨道，TGA是给电子体，矿物是电子受体。对比TGA与方铅矿轨道能量差ΔE1和ΔE2，两者相差不大，这也间接体现了方铅矿中S—Pb呈现较强的共价键的特性，这与Mulliken布居分析一致。对比TGA的HOMO轨道与黄铜矿和方铅矿的LUMO轨道之间的两个能量差ΔE2，发现TGA的HOMO与黄铜矿LUMO之间的轨道能量差明显小于与方铅矿LUMO之间的轨道能量差。根据能量差越小，反应越容易进行的原则，说明当巯基乙酸钠与矿物作用时，TGA的电子更易于转移至黄铜矿的LUMO，从而发生相互作用。因此，采用巯基乙酸钠作为黄铜矿抑制剂来实现铜铅分离理论上是可行的，实验也证实了这一点[29]。
2.4 费米能级讨论
表5所列为经MS软件模拟计算后得到的黄铜矿、方铅矿和TGA离子费米能级。
表5 矿物和巯基乙酸离子的费米能级
Table 5 Fermi energies of mineral and thioglycolic acid
通过表5可以看出，黄铜矿的费米能级要远低于TGA离子的费米能级，这说明，反应时，电子易于从TGA离子转移至黄铜矿，从而使得黄铜矿表面的双黄药发生还原解析，从而得到抑制。而对比方铅矿和TGA离子的费米能级发现，两者非常接近，所以在反应时两者之间发生电子的转移较为困难。因此，从费米能级角度考虑，TGA易于优先同黄铜矿发生作用，这与前线轨道分析一致。
3 结论
1) 通过密度泛函模拟计算方法，得到了黄铜矿和方铅矿的能带结构和态密度，能带结构表明黄铜矿和方铅矿均为直接带隙p型半导体。
2) 黄铜矿费米能级附近主要由Cu-3d和 Fe-3d轨道贡献组成，其中Cu-3d的贡献最多，Fe-3d的次之，两者都具有较高的活性，Mulliken布居表明Cu—S键与Fe—S键相比更趋于离子性；方铅矿费米能级附近主要由Pb-6p和 S-3p轨道组成，Mulliken布居表明两者呈共价键结合。黄铜矿(101)表面和方铅矿(100)表面裸露原子的分态密度与其内部原子相比均出现了明显的变化，解理面的形成使得表面原子活性增强。
3) 利用前线轨道理论计算了黄铜矿、方铅矿与巯基乙酸钠的相互作用能。结果表明：黄铜矿较方铅矿更易于优先与巯基乙酸钠结合，在理论上解释了巯基乙酸钠在铜铅分离中的可行性，这为进一步认识铜铅分离实质及新型抑制剂的研发提供了理论依据和参考。
REFERENCES
[1] 卜勇杰, 刘润清, 孙 伟, 孟庆波. 新型组合抑制剂在低品位铜铅硫化矿浮选分离中的应用[J]. 矿冶工程, 2013, 33(5): 50-52.
BU Yong-jie, LIU Run-qing, SUN Wei, MENG Qing-bo. Application of combined depressant in separation of Cu/Pb in low-grade sulfide ore[J]. Mining and Metallurgical Engineering, 2013, 33(5): 50-52.
[2] 刘润清, 孙 伟, 胡岳华. 铜铅分离有机抑制剂FCLS的研究[J]. 矿冶工程, 2009, 29(3): 29-32.
LIU Run-qing, SUN Wei, HU Yue-hua. Study on organic depressant FCLS for separation of chalcopyrite and galena[J]. Mining and Metallurgical Engineering, 2009, 29(3): 29-32.
[3] 魏明安, 孙传尧. 硫化铜、铅矿物浮选分离研究现状及发展趋势[J]. 矿冶, 2008, 17(2): 6-16.
WEI Ming-an, SUN Chuan-yao. Review and development tendency of the copper and lead sulfides flotation separation[J]. Mining & Metallurgy, 2008, 17(2): 6-16.
[4] 杜延雷, 李成必. 新型有机抑制剂用于硫化铜铅矿物浮选分离的研究[J]. 有色金属(选矿部分), 2013, 6: 86-89.
DU Yan-lei, LI Cheng-bi. Research on the separation of copper-lead ores with a new type of organic depressants by flotation[J]. Nonferrous Metals (Mineral Processing Section), 2013, 6: 86-89.
[5] 迟晓鹏, 王纪镇, 邓海波, 印万忠. 铜铅分离新型铅抑制剂研究[J]. 金属矿山, 2013(11): 56-59.
CHI Xiao-peng, WANG Ji-zhen, DENG Hai-bo, YIN Wan-zhong. Study on a new-type lead depressant for copper and lead separation[J]. Metal Mine, 2013(11): 56-59.
[6] 米丽平, 孙春宝, 李 青, 徐 涛, 刘欣伟. 用组合抑制剂实现铜铅高效分离的试验研究[J]. 金属矿山, 2009(8): 53-56.
Mi Li-ping, SUN Chun-bao, Li Qing, XU Tao, LIU Xin-wei. Experimental study on copper-lead separation with the combinatorial depressant[J]. Metal Mine, 2009(8): 53-56.
[7] BOLIN N J, LASKOWSKI J S. Polysaccharides in flotation of sulfides, PartⅡ: copper/lead separation with dextrin and sodium hydroxide[J]. International Journal of Mineral Processing, 1991, 33: 235-241.
[8] 王中生, 郭月琴. CMC在铜铅分离浮选中的应用[J]. 矿产保护与利用, 2002(1): 30-32.
WANG Zhong-sheng, GUO Yue-qin. Application of CMC in flotation separation of Cu-Pb[J]. Conservation and Utilization of Mineral Resources, 2002(1): 30-32.
[9] AGAR G E. Sulphide depression with thioglycollate of trithiocarbonate[J]. CIM Bull, 1984, 77: 43.
[10] NAGARAJ D R, WANG S S, AVOTINS P V. Copper depressants: Correlation between structure and activity[C]// 112th SME-AIME Annual Meeting. USA: Spring, 1982: 89-93.
[11] POLING G W, LIU Qi. 硫基乙酸浮选抑制黄铜矿的研究[J]. 国外金属矿选矿, 1989(4): 30-36.
POLING G W, LIU Qi. Studies on the flotation depression of chalcopyrite by thioglycollic acid[J]. Metallic Ore Dressing Abroad, 1989(4): 30-36.
[12] TOSSELL J A, VAUGHAN D J. Theoretical studies of xanthates, dixanthogen, metal xanthates and related compounds[J]. Journal of Colloid Interface Science, 1993, 155(1): 98-107.
[13] EDELBRO R, SANDSTROM A, PAUL J. Full potential calculations on electron band structures of sphalerite, pyrite and chalcopyrite[J]. Applied Surface Science, 2003, 206(1/4): 300-313.
[14] 陈建华, 王进明, 龙贤灏, 郭 进. 硫化铜矿物电子结构的第一性原理研究[J]. 中南大学学报(自然科学版), 2011, 42(12): 3612-3617.
CHEN Jian-hua, WANG jin-ming, LONG Xian-hao, GUO Jin. First-principle theory on electronic structure of copper sulfides[J]. Journal of Central South University (Science and Technology), 2011, 42(12): 3612-3617.
[15] ZHAO Cui-hua, CHEN Jian-hua, WU Bo-zeng, LONG Xian-hao. Density functional theory study on natural hydrophobicity of sulfide surfaces[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(2): 491-498.
[16] CHEN Jian-hua, WANG Lei, CHEN Ye, GUO Jin. A DFT study of the effect of natural impurities on the electronic structure of galena[J]. International Journal of Mineral Processing, 2011, 98: 132-136.
[17] CHEN Ye, CHEN Jian-hua, GUO Jin. A DFT study on the effect of lattice impurities on the electronic structures and floatability of sphalerite[J]. Minerals Engineering, 2010, 23: 1120-1130.
[18] CHEN Jian-hua, LAN Li-hong, CHEN Ye. Computational simulation of adsorption and thermodynamic study of xanthate, dithiophosphate and dithiocarbamate on galena and pyrite surfaces[J]. Minerals Engineering, 2013, (46/47): 136-143.
[19] ZHAO Cui-hua, CHEN Jian-hua, LONG Xian-hao, GUO Jin. Study of H2O adsorption on sulfides surfaces and thermokinetic analysis[J]. Journal of Industrial and Engineering Chemistry, 2014, 20: 605-609.
[20] CHEN Jian-hua, LONG Xian-hao, CHEN Ye. Comparison of multilayer water adsorption on the hydrophobic galena (PbS) and hydrophilic pyrite (FeS2) surfaces: A DFT study[J]. J Phys Chem C, 2014, 118(22): 11657-11665.
[21] von OERTZEN G U, JONES R T, GERSON A R. Electronic and optical properties of Fe, Zn and Pb sulfides[J]. J Electron Spectrosc, 2005, 144/147(6): 1245-1247.
[22] JONES R O, GUNNARSSON O. The density functional formalism, its application and prospects[J]. Review of Modern Physics, 1989, 61(3): 689-746.
[23] PERDEW J P, BURKE K, ERNEZERHOF M. Generalized gradient approximation made simple[J]. Phys Rev Lett, 1996, 77(18): 3865-3868.
[24] PERDEW J P, WANG Y. Accurate and simple analytic representation of the electron-gas correlation energy[J]. Phys Rev B, 1992, 45: 13244-13249.
[25] 张 麟. 铜录山铜矿浮选基础研究与应用[D]. 长沙: 中南大学, 2009.
ZHANG Lin. Basic researches on flotation of copper minerals of Tonglunshan Mine and application[D]. Changsha: Central South University, 2009.
[26] 陈建华, 王 檑, 陈 晔, 李玉琼, 郭 进. 空位缺陷对方铅矿电子结构及浮选行为影响的密度泛函理论[J]. 中国有色金属学报, 2012, 20(9): 1815-1821.
CHEN Jian-hua, WANG Lei, CHEN Ye, LI Yu-qiong, GUO Jin. Density functional theory of effects of vacancy defects on electronic structure and flotation of galena[J]. The Chinese Journal of Nonferrous Metals, 2012, 20(9): 1815-1821.
[27] MULLIKEN R S. Electronic population analysis on LCAO-MD molecular wave functions[J]. J Chem Phys, 1955, 23: 1833-1840.
[28] FUKUI K, KOGA N, FUJIMOTO H. Interaction frontier orbitals[J]. J Am Chen Soc, 1981, 103(1): 196-197.
[29] 陈慧杰, 蒋升国, 李吉云, 张 莉. 巯基乙酸钠在铜铅分离中的应用研究[J]. 矿业研究与开发, 2011, 31(6): 68-70.
CHEN Hui-jie, JIANG Sheng-guo, LI Ji-yun, ZHANG Li. Application research on flotation separation of copper-lead with sodium thioglycollate[J]. Mining R&D, 2011, 31(6): 68-70.
Depressing mechanism of copper-lead separation by density functional theory method
ZHANG Xing-rong, LIU Chong-jun, ZHU Yang-ge, ZHENG Gui-bing, SHANG Yan-bo, HAN Long, AI Jing
(State Key Laboratory of Mineral Processing, Beijing General Research Institute of Mining and Metallurgy, Beijing 102600, China)
Abstracts: In order to discuss the separation mechanism of copper-lead ore, the crystal and surface electronic structures of chalcopyrite and galena were studied, by density functional theory (DFT), based on quantum chemistry. The results show that differences of the electronic structure of chalcopyrite and galena could directly affect their floatabilities, such as band structure, density of states, Mulliken populations, and so on. And the frontier orbitals of chalcopyrite and galena were also calculated, from which the interaction energies between minerals and TGA were obtained and compared. So, the essence of flotation separation of copper and galena were well revealed.
Key words: density functional theory; chalcopyrite; galena; depressant; separation
Foundation item: Project(2013AA064101) supported by the National High Research Development Program of China; Project(2015DFA60330) supported by the National Science and Technology Cooperation of China
Received date: 2016-03-11; Accepted date: 2016-07-07
Corresponding author: ZHU Yang-ge; Tel: +86-10-59069508; E-mail: zhuyangge@bgrimm.com
(编辑 王 超)
基金项目：国家高技术研究发展计划资助项目(2013AA064101)；国家国际科技合作专项项目(2015DFA60330)
收稿日期：2016-03-11；修订日期：2016-07-07
通信作者：朱阳戈，高级工程师，博士；电话：010-59069508；E-mail: zhuyangge@bgrimm.com
