Robust range-parameterized cubature Kalman filter for bearings-only tracking
来源期刊:中南大学学报(英文版)2016年第6期
论文作者:吴昊 陈树新 杨宾峰 罗玺
文章页码:1399 - 1405
Key words:bearings-only tracking; nonlinearity; cubature Kalman filter; numerical integration; equivalent weight function
Abstract: In order to improve tracking accuracy when initial estimate is inaccurate or outliers exist, a bearings-only tracking approach called the robust range-parameterized cubature Kalman filter (RRPCKF) was proposed. Firstly, the robust extremal rule based on the pollution distribution was introduced to the cubature Kalman filter (CKF) framework. The improved Turkey weight function was subsequently constructed to identify the outliers whose weights were reduced by establishing equivalent innovation covariance matrix in the CKF. Furthermore, the improved range-parameterize (RP) strategy which divides the filter into some weighted robust CKFs each with a different initial estimate was utilized to solve the fuzzy initial estimation problem efficiently. Simulations show that the result of the RRPCKF is more accurate and more robust whether outliers exist or not, whereas that of the conventional algorithms becomes distorted seriously when outliers appear.
J. Cent. South Univ. (2016) 23: 1399-1405
DOI: 10.1007/s11771-016-3192-z
WU Hao(吴昊), CHEN Shu-xin(陈树新), YANG Bin-feng(杨宾峰), LUO Xi(罗玺)
Information and Navigation College, Air Force Engineering University, Xi’an 710077, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: In order to improve tracking accuracy when initial estimate is inaccurate or outliers exist, a bearings-only tracking approach called the robust range-parameterized cubature Kalman filter (RRPCKF) was proposed. Firstly, the robust extremal rule based on the pollution distribution was introduced to the cubature Kalman filter (CKF) framework. The improved Turkey weight function was subsequently constructed to identify the outliers whose weights were reduced by establishing equivalent innovation covariance matrix in the CKF. Furthermore, the improved range-parameterize (RP) strategy which divides the filter into some weighted robust CKFs each with a different initial estimate was utilized to solve the fuzzy initial estimation problem efficiently. Simulations show that the result of the RRPCKF is more accurate and more robust whether outliers exist or not, whereas that of the conventional algorithms becomes distorted seriously when outliers appear.
Key words: bearings-only tracking; nonlinearity; cubature Kalman filter; numerical integration; equivalent weight function
1 Introduction
The bearings-only passive tracking plays an important role in many fields, such as navigation and military applications [1-3]. It is a typical nonlinear filtering problem to estimate the position and velocity of a moving target through bearing measurements from a single platform [4].
In the Bayesian framework, solutions to the nonlinear problem can be classified into two categories. The first category contains filters that are suitably applied to the non-Gaussian systems, such as the particle filter (PF) [5-7] and the Gaussian mixture filter [8-10]. They require no prior assumption of the posterior probability density but suffer from enormous computational complexity. Based on the Gaussian assumption of posterior probability density, the filters in the second category can be executed simply and quickly. They mainly include the extended Kalman filter (EKF) [11-12], the unscented Kalman filter (UKF) [13-16], and the cubature Kalman filter (CKF) [17-18]. Among these filters, the CKF approximates the posterior density according to the third-degree spherical radial cubature rule and has drawn much attention in recent years. Compared with the EKF, the CKF is a derivative-free filter and preforms higher accuracy. On the other hand, the CKF shows better numerical stability and lower computational demands than the UKF in the high dimension [19-20]. As a consequence, the CKF is more suitable for bearings-only tracking.
Theoretically, if measurements are reliable, the CKF will provide an accurate and stable tracking result. Unfortunately, the measurement noises are not always strictly following Gaussian distribution, and the measurements can be easily polluted by outliers in military application or in other bad conditions. PESONEN and PICHE [21] showed that the probability of outliers in measurements is about 1%-10%. For the case when uncertain outliers appear, the tracking result will become unreliable. Some pre-processing methods, such as the threshold setting, may work in some situations. However, they generally require the statistical property of unknown interference distribution. Even worse, the “hard decision” methods can easily fail when outliers are close to the threshold. Thus, an effective robust filter is needed. In addition, the CKF-based algorithms are sensitive to the initial estimate, and bad initial estimate may also lead to poor tracking accuracy [22].
Considering the problems, the robust range- parameterized cubature Kalman filter (RRPCKF) algorithm was proposed in this paper. The pollution distribution was first introduced to the standard CKF, and the innovation covariance matrix was modified through the improved equivalent weight function which can identify outliers and reduce the weights of the outliers. To solve the fuzzy initial estimation problem, the range-parameterized (RP) strategy which consists a series of weighted sub-filters with different initial estimates can be paralleled [22], where the weights of those with better initial estimates were increased. Low weighted sub-filters were then removed according to the threshold which was set to reduce the computational complexity. Moreover, the equivalent weight and the weight delay strategy were introduced to make the RP trackers calculable when outliers appear.
2 Cubature Kalman filter for bearings-only tracking
2.1 Tracking model
As shown in Fig. 1, we assume that the target is in uniform linear motion with acceleration disturbance, so that the state vector at time index k can be expressed by 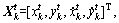 where
where  is the position and
is the position and 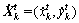 is the velocity vector. Here, k=1, 2, …, n, where n is measurement times. The true state of the observation platform is
is the velocity vector. Here, k=1, 2, …, n, where n is measurement times. The true state of the observation platform is  and the state vector in the relative own-ship reference at time index k can be defined as
and the state vector in the relative own-ship reference at time index k can be defined as
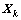



Fig. 1 tracking model
The dynamic model is written as
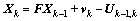 (1)
(1)
where Uk-1,k is the deterministic input and F is the state transition matrix, which can be given by


△t is the measurement interval, and vk represents the process noise vector which is generally assumed independent and identically distributed zero mean Gaussian noise with a covariance matrix as
 (2)
(2)
where q represents the intensity of the process noise, and Γ is noise drive matrix:

The measurement model is denoted as
 (3)
(3)
where ek is generally assumed to be zero mean Gaussian measurement noise, and the standard deviation is σz.
2.2 Cubature Kalman filter
The cubature Kalman filter uses the third-degree spherical-radial rule to numerically approximate the multi-dimensional integral involved in Bayesian filtering. The cubature points and their weights can be obtained from the spherical-radial rule:
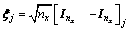 (4)
(4)
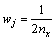 (5)
(5)
where nx is the state dimension;  is the identity matrix with the dimension of nx; and [·]j represents the jth column of [·], j=1, 2, …, 2nx.
is the identity matrix with the dimension of nx; and [·]j represents the jth column of [·], j=1, 2, …, 2nx.
At the time update stage, the dynamic model is linear, so the predicted state and corresponding predicted covariance can be described as
 (6)
(6)
 (7)
(7)
At the beginning of the measurement update stage, the predicted covariance is factorized as
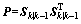 (8)
(8)
Then evaluate the cubature points:
 (9)
(9)
In order to approximate the posterior density, the cubature points are propagated according to the measurement equation:
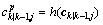 (10)
(10)
Accordingly, the predicted measurement can be estimated as
 (11)
(11)
The Kalman gain is given by
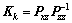 (12)
(12)
where the innovation covariance matrix and the cross covariance matrix are:
 (13)
(13)
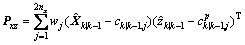 (14)
(14)
Therefore, the predicted state and the corresponding covariance can be updated as
 (15)
(15)
 (16)
(16)
3 Robust range-parameterized cubature Kalman filter
3.1 Robust CKF
In practical applications, whether measurement noises follow Gaussian distribution exactly cannot be guaranteed. The outliers may lead to inaccurate performance in bad conditions. Thus, the pollution distribution is introduced as [23]
 (17)
(17)
where Fd is the dominated distribution, Qd is the interference distribution, and ε is the rate of the polluted measurements in all the measurements. In order to obtain an accurate and robust result, both Fd and Qd should be considered.
The residual at time index k can be expressed as
 (18)
(18)
which represents the error in measurement. When outlier occurs, the residual will become abnormal so that it can be utilized to identify the outlier. Then the weight of polluted measurement can be reduced by improving the innovation covariance:
 (19)
(19)
where  and
and  is the equivalent weight factor at time index k. Equation (19) shows that the unknown outlier is regarded as the noise coming from the interference distribution Qd, where the covariance is equivalent to
is the equivalent weight factor at time index k. Equation (19) shows that the unknown outlier is regarded as the noise coming from the interference distribution Qd, where the covariance is equivalent to 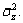 Obviously, the method according to the pollution distribution is more reasonable than some pre-processing methods.
Obviously, the method according to the pollution distribution is more reasonable than some pre-processing methods.
Afterwards, the equivalent Kalman gain, the equivalent state and the corresponding covariance can be given by
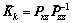 (20)
(20)
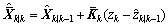 (21)
(21)
 (22)
(22)
The above discussion implies that the key to reduce the effect of outliers is the designing of the equivalent weight function. It generally consists of two parts: the division of measurement residual and the corresponding weight of each interval. It is called two piecewise weight method when the measurement residual is divided into normal information and abnormal information, such as the division in Huber method and Danish method [21, 24]. Moreover, the abnormal information can be divided into available information and harmful information, then the weight of the available information can be reduced and that of the harmful information can be eliminated, i.e. Turkey weight function [21] is:
 (23)
(23)
In the CKF, if wm(k) is zero or close to zero, Pzz will become infinite, and the tracking result may be distorted or even divergent. In fact, the effect of outliers on tracking is limited because bearings are bounded. Hence improved Turkey weight function is presented to avoid  being close to zero when outliers are large:
being close to zero when outliers are large:
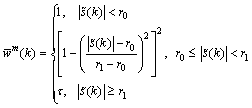 (24)
(24)
where  is the standard residual, and τ is a small positive number. r0 and r1 represent the sensitivity of the weight function to outliers. In general, the appropriate r0 and r1 are related to the confidence coefficient of the pollution distribution. If less prior information is utilized, the experience value
is the standard residual, and τ is a small positive number. r0 and r1 represent the sensitivity of the weight function to outliers. In general, the appropriate r0 and r1 are related to the confidence coefficient of the pollution distribution. If less prior information is utilized, the experience value  will also make the result robust.
will also make the result robust.
3.2 Robust range-parameterized CKF
The initial estimate may be far away from the true value, and then the above robust CKF will also provide poor performance, which is partly due to the lack of range information in bearings-only tracking. Following this, a series of weighted robust CKFs with different initial values can be utilized for tracking, where their weights are determined by the accuracy of the initial estimates.
Assume that the interval of initial estimate range is (rmin, rmax), and they are divided into NF subinterval with geometric progression [22]. The common ratio of the geometric progression is:
 (25)
(25)
So the mean and standard deviation of the range prior in each subintervals are:
 (26)
(26)
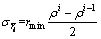 (27)
(27)
where i=1, 2, …, NF. At time index k, the state and covariance of each independent robust CKF tracker are updated according to Eqs. (6)-(16). In addition, the weight of the sub-filter is updated using the Bayesian theorem, which can be calculated as
 (28)
(28)
where  is the measurement likelihood of the ith robust CKF tracker at time index k. It is given by:
is the measurement likelihood of the ith robust CKF tracker at time index k. It is given by:
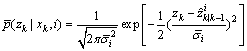 (29)
(29)
where 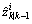 is the predicted measurement for the ith filter, and
is the predicted measurement for the ith filter, and  is its equivalent innovation covariance.
is its equivalent innovation covariance.
Therefore, the estimated state and covariance at time index k can be obtained by:
 (30)
(30)
 (31)
(31)
where  and
and  are the estimated state and covariance of the ith filter at time index k, respectively.
are the estimated state and covariance of the ith filter at time index k, respectively.
In most cases, the weights of some sub-filters rapidly decrease and are close to zero. It is also necessary to remove those trackers which have become unstable. Thus a weight threshold γ is set to control the quantity of sub-filters. When 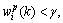
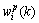 can be set to zero, and the weights of remaining filters can be recalculated according to Eq. (28). It not only reduces the calculation, but also improves the accuracy and stability of the RRPCKF tracker.
can be set to zero, and the weights of remaining filters can be recalculated according to Eq. (28). It not only reduces the calculation, but also improves the accuracy and stability of the RRPCKF tracker.
Outliers also affect the stability of measurement likelihood. If measurement likelihood become abnormal, the weight of corresponding sub-filter will become incalculable. Actually, the equivalent innovation covariance can improve measurement likelihood effectively according to Eqs. (28) and (29). Otherwise, if  is still incalculable,
is still incalculable, 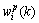 can be set the same as previous weight at time index k-1 to keep the RRPCKF tracker robust. The method is called the weight delay strategy.
can be set the same as previous weight at time index k-1 to keep the RRPCKF tracker robust. The method is called the weight delay strategy.
4 Simulation
4.1 Initialization
It is assumed that the target is in uniform linear motion with acceleration disturbance, where the process noise intensity q is 10-12 km2/s3 and measurement interval △t=1 min. Although the motion of the observation platform is important for tracking, we focus on the filtering algorithms in this work. Thus, the observation platform is also assumed to be in uniform linear motion, where the initial position is (0, 0), the speed is 5 km/h, and the course is 100°.
The position root mean square error (RMSEpos) at time index k is defined as
 (32)
(32)
where L is Monte Carlo times, which is set to 200 here. Similarly, the RMSE in velocity (RMSEvel) can be easily written according to the RMSEpos.
In the Monte Carlo test, the target begins at the same state every time for fair comparison. The scale parameter κ of the UKF is set as 3-nx, and the algorithms (the UKF and the CKF) are set as the same initial conditions. The initial range estimate follows 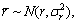 where r is the true range. The initial bearing follows
where r is the true range. The initial bearing follows  , where z0 is the true bearing. Similarly, the initial velocity estimate
, where z0 is the true bearing. Similarly, the initial velocity estimate  where s is the true initial target velocity. The target course estimate follows
where s is the true initial target velocity. The target course estimate follows 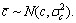 The parameters in simulation scenario are shown in Table 1.
The parameters in simulation scenario are shown in Table 1.
In the RPCKF [22], NF=5 independent CKFs are utilized, and the initial range interval is given by rmin=r-3σr and rmax=r+3σr. When r-3σr<0, we set rmin=0.1r. The initial weight of each filter is 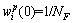 (i=1, 2, …, NF). Other parameters are initialized similar to the CKF.
(i=1, 2, …, NF). Other parameters are initialized similar to the CKF.
In the RRPCKF, the weight threshold γ=0.01 and the improved Turkey function is used to resist outliers, where r0=1.8, r1=6, and τ=10-3. When outliers appear, the RP tracker will be seriously unstable, hence the equivalent innovation covariance  and the weight delay strategy are both used. Other initializations are the same as those of the RPCKF.
and the weight delay strategy are both used. Other initializations are the same as those of the RPCKF.
Table 1 Parameters of tracking

4.2 Simulation and analysis
Simulation experiment 1: no outliers in the measurements. The RMSEs in position and velocity are shown in Fig. 2.
Simulation experiment 2: continuous outliers in the measurements. They appear in 26-30 min, with the intensity of 4σz. The RMSEs in position and velocity are shown in Fig. 3.
Simulation experiment 3: Large outlier in the measurement. It appears in 30min, with the intensity of 60σz. The RMSEs in position and velocity are shown in Fig. 4.

Fig. 2 RMSEs of algorithms when no outliers:
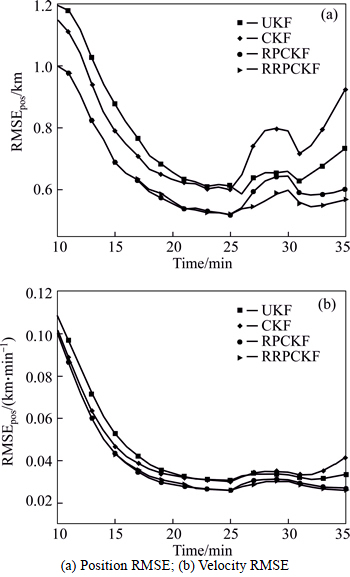
Fig. 3 RMSEs of algorithms when continuous outliers exist:

Fig. 4 RMSEs of algorithms when large outliers exist:
As shown in Fig. 2(a), when there are no outliers in the measurements, all algorithms are close to convergent with the measurement times increasing. By the end of the Monte Carlo test, the CKF-based algorithms outperform the UKF. One explanation is that the negative κ may lead to non-positive definiteness of the covariance matrices. In addition, the RPCKF and RRPCKF perform more accuracy than other algorithms. This is because the RP strategy in the RPCKF and improved version in the RRPCKF can improve the weight of the sub-filter whose initial range estimate matches the target range. It can be seen in the Fig. 2(a) that the curves of the RRPCKF and RPCKF almost overlap, which illustrate that appropriate equivalent weight function is hardly affecting the accuracy of the RRPCKF when there are no outliers. The RRPCKF keeps higher efficiency and less computational complexity than the RPCKF. The same conclusions can be obtained according to Fig. 2(b).
When the measurements are subject to the pollution of continuous small outliers and large outlier (26-30 min in Fig. 3 and 30 min in Fig. 4, respectively), the results of the UKF, CKF and RPCKF become obviously distorted, whereas that of the RRPCKF still keeps accurate comparatively. This is because the improved Turkey function of the RRPCKF reduces the weights of the inaccurate measurements according to the residuals and bounds the bad effect effectively. On the contrary, other algorithms regard outliers as normal measurements, and they do not in accord with real situations. What is worse, the UKF and the CKF tend to divergent after the outliers’ interference, on account of the deterioration of covariance matrices. Additionally, it is noteworthy that the large outlier makes the likelihood function infinite in the traditional RP strategy and it is the reason why the RPCKF becomes incalculable.
5 Conclusions
1) To deal with the inaccuracy caused by outliers in bearings-only tracking, the robust estimation theory is introduced to the CKF framework. Furthermore, the new equivalent weight function called the improved Turkey function is presented. It can identify the outliers automatically and reduce the weights of the continuous small outliers and large outliers efficiently.
2) The improved RP strategy is constructed to solve the fuzzy initial estimation problem. Setting the weight threshold further reduces the calculation, and the equivalent likelihood in conjunction with the weight relay strategy makes the weights of sub-filters calculable when outliers appear.
3) Simulation shows that the proposed algorithm can greatly guarantee both the accuracy and robustness of the tracking, and it is potentially applied to the nonlinear filter problem in bad conditions.
References
[1] WANG S Y, FENG J C, TSE C K. Analysis of the characteristic of the Kalman gain for 1-D chaotic maps in cubature Kalman filter [J]. IEEE Signal Processing Letters, 2013, 20(3): 229-232.
[2] SON H S, PARK J B, JOO Y H. Fuzzy c-means clustering-based smart tracking model for three-dimensional manoeuvring target including unknown acceleration input [J]. IET Radar, Sonar and Navigation, 2013, 7(6): 623-634.
[3] ITO K, XIONG K Q. Gaussian filters for nonlinear filtering problems [J]. IEEE Transactions on Automatic Control, 2000, 45(5): 910-927.
[4] JAUFFRET C, PILLON D, PIGNOL A C. Bearings-only maneuvering target motion analysis from a nonmaneuvering platform [J]. IEEE Transactions on Aerospace Electronic Systems, 2010, 46(4): 1934-1949.
[5] YANG T, MEHTA P G, MEYN S P. Feedback particle filter [J]. IEEE Transactions on Automatic Control, 2013, 58(10): 2465-2480.
[6] DOUCET A, GADSILL S, ANDRIEU C. On sequential Monte Carlo sampling methods for Bayesian filtering [J]. Statistics and Computing, 2000, 50(2): 736-746.
[7] ZUO J Y. Dynamic resampling for alleviating sample impoverishment of particle filter [J]. IET Radar, Sonar & Navigation, 2013, 7(9): 968-977.
[8] MACAGNANO D, de ABREU G T F. Adaptive gating for multitarget tracking with Gaussian mixture filters [J]. IEEE Transactions on Signal Processing, 2012, 60(3): 1533-1538.
[9] BILIK I, TABRIKIAN J. Maneuvering target tracking in the presence of glint using the nonlinear Gaussian mixture Kalman filter [J]. IEEE Transactions on Aerospace Electronic Systems, 2010, 46(1): 240-262.
[10] CLARK J M C, KOUNTOURIOTIS P A, VINTER R B. A Gaussian mixture filter for range-only tracking [J]. IEEE Transactions on Automatic Control, 2011, 56(3): 602-613.
[11] AHMED N U, RADAIDEH S M. Modified extended Kalman filtering [J]. IEEE Transactions on Automatic Control, 1994, 36(6): 1322-1326.
[12] LIU C, SHUI P, LI S. Unscented extended Kalman filter for target tracking [J]. Journal of Systems Engineering and Electronics, 2011, 22(2): 188-192.
[13] JULIER S J, UHLMANN J K. A new method for the nonlinear transformation of means and covariances in filters andestimators [J]. IEEE Transactions on Automatic Control, 2000, 45(3): 477-482.
[14] JULIER S J, UHLMANN J K. Unscented filtering and nonlinear estimation [J]. Proceedings of the IEEE , 2004, 93(3): 401-422.
[15] CHANG G B. Marginal unscented kalman filter for cross-correlated process and observation noise at the same epoch [J]. IET Radar, Sonar & Navigation, 2014, 8(1): 54-64.
[16] LIU Kai-Zhou, LI Jing, GUO Wei, ZHU Pu-qiang, WANG Xiao-hui. Navigation system of a class of underwater vehicle based on adaptive unscented Kalman filter algorithm [J]. Journal of Central South University, 2014, 21(2): 550-557.
[17] ARASARATNAM I, HAYKIN S. Cubature Kalman filters [J]. IEEE Transactions on Automatic Control, 2009, 54(06): 1254-1269.
[18] JIA B, XIN M, CHENG Y. High-degree cubature Kalman filter [J]. Automatica, 2013, 49(2): 510-518.
[19] ARASARATNAM I, HAYKIN S. Cubature Kalman smoothers [J]. Automatica, 2011, 47(10): 2245-2250.
[20] PESONEN H, PICHE’ R. Cubature-based Kalman filters for positionin [M]. IEEE 2010 7th Workshop on Positioning, Navigation and Communication. 2010: 45-49.
[21] YANG Y X. Adaptive navigation and kinematic positioning [M]. Beijing, China: Surveying and Mapping Press, 2006. (in Chinese)
[22] LEONG P H, ARULAMPALAM S, LANAHEWA T A, ABHAYAPALA T D. A Gaussian-sum based cubature Kalman filter for bearings-only tracking [J]. IEEE Transactions on Aerospace Electronic Systems, 2013, 49(2): 1161-1176.
[23] TUKEY J W. A survey of sampling from contaminated distributions in contributions to probability and statistics [M]. Stanford Calif: Stanford University Press, 1960.
[24] LI W, LIU M H, DUAN D P. Improved robust Huber-based divided difference filtering [J]. Proceedings of the Institution of Mechanical Engineers. Part G, Journal of Aerospace Engineering, 2014, 228(11): 2123-2129.
(Edited by DENG Lü-xiang)
Foundation item: Projects(51377172, 51577191) supported by the National Natural Science Foundation of China
Received date: 2015-03-25; Accepted date: 2015-09-23
Corresponding author: WU Hao, PhD Candidate; Tel: +86-29-84791523; E-mail: wuhaostudy@163.com

