DOI： 10.11817/j.issn.1672-7207.2020.02.026

裂隙岩体渗流-传热的时域半解析计算方法

刘东东,项彦勇

（北京交通大学 土木建筑工程学院，北京，100044）

摘要:针对饱和裂隙岩体渗流-传热问题，提出一种时域半解析计算方法。首先利用三维热传导方程的基本解建立岩石温度的时空域边界积分方程，通过对时间进行卷积积分将其简化为空间域的积分方程；应用有限单元法离散裂隙水的热对流方程，建立线性代数方程组，经过迭代计算直接得到裂隙水和岩石的温度。最后，通过1个核废处置库裂隙岩体渗流-传热算例,验证本文方法的有效性。研究结果表明：相比于拉氏变换半解析方法，本文方法具有计算过程更简单和计算结果更精确的特点，能用于分析稀疏裂隙系统中的水流-传热问题;裂隙水将核废物释放的热量传输至下游，有利于降低处置库温度。

关键词:裂隙岩体；饱和渗流；三维传热；时域半解析方法

中图分类号:P314      文献标志码:A                开放科学(资源服务)标识码(OSID)

文章编号:1672-7207（2020）02-0523-09

Temporal semi-analytical method for water flow and heat transfer in fractured rocks

LIU　Dongdong, XIANG　Yanyong

(School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China)

Abstract: In view of the water flow and heat transfer in fractured-rock matrix, a temporal semi-analytical method was proposed. First, a boundary integral equation of rock temperature in spatial-temporal domain was established by using the fundamental solution of the three-dimensional heat conduction, and then the equation was simplified into a spatial domain equation by implementing convolution integral over time. Then, linear algebraic equations were formulated by combining the finite element equation of thermal convection in fracture water and previous boundary integral equation of rock temperature. Finally, the temperature of fracture water and rock matrix was solved by manipulating an iterative calculation. A numerical example of water flow and heat transfer in a nuclear waste repository was provided to verify the effectiveness of the proposed method. The results show that compared with the existing Laplace transformation semi-analytical method, the poroposed method in the paper is simpler and more accurate, and applicable to heat transfer problems of fractured-rock matrix with multiple parallel fractures distributed. The fracture water transfers the heat that is emitted from nuclear waste downstream, which contributes to the decline of repository temperature.

Key words: fractured rock; saturated seepage; three dimensional heat transfer; temporal semi analytical method

对于高放废物的处置，建造地下处置设施进行隔离是目前国际上普遍接受且技术上可行的方案^[1]。处置系统的安全性取决于工程屏障系统(废物体、废物罐、缓冲材料和回填材料等子系统)和天然屏障系统(近场、远场、地下水、生物圈和环境等子系统)的综合阻隔能力。其中，地下水子系统由岩体中的孔隙水和裂隙水组成，是核污染物运移的主要载体。在处置系统运行期间，高放废物会在较长时间内发生衰变并产生很高的热量，使得近场围岩温度升高，改变其物理、化学性质，可能形成传热(T)、渗流(H)、应力(M)及化学反应(C)的多场耦合作用，降低多重屏障系统的隔离功能。作为中国高放废物处置库首预选区，甘肃北山的主岩为致密的花岗岩，其孔隙极不发育，但有稀疏裂隙分布^[2]，因此，裂隙水流场成为影响北山处置库阻滞能力的关键因素之一。要评价处置主岩的性能，需要研究渗流-传热耦合条件下近场裂隙岩体的响应。一般而言，裂隙岩体渗流-传热过程涉及非线性的数学问题，通常采用数值方法求解。例如，对于单一孔隙介质，张玉军^[3]建立了适合饱和与非饱和孔隙介质的二维THM耦合方程并给出了相应的有限元求解方法，对高放废物处置库近场围岩TMH耦合过程进行了初步模拟研究，分析了温度、饱和度和孔隙水压力随时间的变化趋势，并把二维分析拓展到三维分析^[4]；对于双重孔隙介质，张玉军等^[5]建立了二维THM耦合方程及其有限元计算方式。但是，上述计算方式不能很好地处理岩石渗透率极低而岩体却有稀疏裂隙分布的渗流-传热问题。鉴于此，基于二维等效孔隙介质模型，柴军瑞^[6]建立了考虑温度和渗流双向耦合作用的有限元数学模型，但由于温度与渗透系数的关系是通过经验公式来表述，因而，该方法对于裂隙网络介质的求解存在一定的局限性；刘学艳等^[7]利用积分有限差分程序TOUGH2模拟了规则裂隙米尺度岩体的加热/注水试验，进一步分析了恒定热源作用下岩体中TH耦合特征的演化规律，但没有考虑热源强度随时间的变化。对于离散裂隙网络模型，王如宾等^[8-9]假定裂隙水流温度沿流动方向呈线性变化，采用解析法和FEPG有限元软件分别计算了单裂隙水流对岩体温度场的影响，实质上施加了裂隙水流温度已知的边界条件。此外，由于需要对整个物理模型进行离散，现有的商用软件被用于高放废物处置库的多场耦合分析时对计算机的存储能力和计算性能要求很高。为了更加有效地描述多场耦合过程，学者们采用了半解析方法对高放废物处置裂隙岩体多场耦合的简化模型进行了求解。例如，项彦勇等^[10]考虑岩石中的二维热传导，建立了单裂隙岩体二维渗流-传热模型，提出了岩石和裂隙水温度的拉氏变换半解析方法，通过数值拉氏逆变换得到时间域上的解答，之后把二维分析拓展到了三维分析^[11-12]。拉氏变换半解析方法虽然避免了对时间积分，但存在计算过程复杂和计算精度较低等问题。为此，本文作者将裂隙岩体中的水-岩热交换集度视作虚拟热源，利用瞬时热源作用下岩石温度的基本解，建立关于时间和空间的边界积分方程，通过卷积积分将其简化为空间域上的积分方程，应用有限元方法离散裂隙水的热对流方程，建立线性代数方程组，经过迭代计算直接得到任意时刻裂隙水和岩石的温度，称之为时域半解析计算方法。本文先计算无内热源时裂隙水的温度，并与拉氏变换半解析解进行对比，最后分析衰变热源作用下裂隙岩体的渗流-传热过程。

1 概念模型与控制微分方程

本研究基于以下假定条件^[9]：

1) 视岩体为无限大介质，忽略岩石本体的渗透性，地下水仅在裂隙内流动；

2) 将裂隙视为平行板状窄缝，裂隙长度远大于隙宽；

3) 岩石和裂隙的热物理性质都不随温度变化而改变，其中裂隙内水流为稳定不可压层流。

图1　单裂隙岩体三维渗流-传热模型

Fig. 1　Three dimensional water flow and heat transfer model of single planar fractured rocks

单裂隙岩体三维渗流-传热模型如图1所示。图1中，裂隙面A的边界可以为任意形状，裂隙开度为w；裂隙水的单宽流量为q，质量密度为ρ_w，比热容为c_w、导热系数为λ_w；裂隙两侧岩石Ω的质量密度为ρ_r，比热容为c_r、导热系数为λ_r；岩石内部存在线热源Γ，其强度为；裂隙水入流截面A_w上的温度为T^*；裂隙水和岩石的初始温度、岩体无穷远处的温度都为T₀。

假设裂隙平行于x-y平面。由于裂隙开度很小，取平面为水-岩交界面。采用水-岩局部热平衡假定，忽略热存储、热传导和热流散效应，则裂隙水的热能守恒方程为^[13]

(1)

式中：；▽₂为二维哈密尔顿算子；h为水-岩热交换集度；t为时间；T为温度。

考虑三维热传导，则岩石的热能守恒方程为^[14]

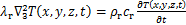(2)

式中：为三维拉普拉斯算子。

模型的初始条件和边界条件为

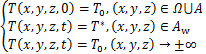(3)

2 积分方程

2.1　时空域边界积分方程

根据三维热传导理论，t'时刻位于岩石基点处的单位点热源在时刻岩石场点处产生的温增为^[14]

             (4)

式中：。

将水-岩热交换集度视为虚拟热源，并考虑线热源放出的热量，则点X的温度为

(5)

式中：=()，为线热源上某一点的坐标。

2.2　时间域离散

把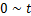离散为N个间隔，认为水-岩热交换集度和线热源强度在每个间隔期间保持不变，则

式(5)可表示为

(6)

式中：，；h (X, t_n)和(, t_n)分别为期间的水-岩热交换集度和线热源强度。

对式(6)中的t'运用卷积积分，则有

(7)

式中：为在上的积分，即；为余误差函数；为岩石的热扩散系数。

2.3　空间域离散

2.3.1　关于裂隙面的积分　

裂隙面网格划分如图2所示，把裂隙面A离散为M个四边形等参单元，共包含K个节点。

图2　裂隙面网格划分

Fig. 2　Meshing of the fracture planar

根据双线性插值理论，单元内部的物理量可以由节点值近似表示为^[15]

(8)

式中：下标m和l分别为单元编号和单元节点编号；N_l，，和分别为l节点对应的插值形函数、裂隙水温度、水-岩热交换集度和裂隙单宽水流量。

插值形函数取Lagrange多项式，即^[15]

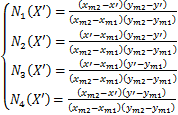(9)

将式(8)和式(9)代入式(7)，则有：

(10)

式中：A_m表示第m个单元的区域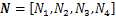；，为插值形函数横向量；，为单元节点水-岩热交换集度列向量。

令

(11)

(12)

式中：，为所有节点水-岩热交换集度列向量；Ｘ_k为第k个节点的坐标。由于矩阵C₁和C₂中的核函数含有1/r，当r →0时积分出现奇异，需要用特殊方法进行处理。

1) 不包含奇点的单元积分。坐标变换如图3所示。当计算点(x, y)位于m单元外时，利用式(13)^[15]把全局坐标系下的A_m区域转换成局部坐标系下的区域。

图3　坐标变换示意图

Fig. 3　Diagram of coordinate transformation

    (13)

采用高斯数值法^[15]，则矩阵C₁和C₂中关于不包含奇点单元的积分为

(14)

式中：；；，为Ｘ的局部坐标；为高斯点的坐标；φ_i和φ_j为高斯点Ψ_ij的权重；N_ξ和N_η分别为ξ和η的不同取值数。

2) 包含奇点的单元积分。若为计算点，则该点为奇点，以此为例说明矩阵C₁和C₂中的奇异积分。

包含奇点的单元再划分如图4所示。以(x_m1, y_m1)为圆心、r_c为半径，将m单元划分为扇形区域A¹ _m和不规则区域A² _m这2个部分。

图4　包含奇点的单元再划分

Fig. 4　Remeshing an element including a singular point

矩阵C₁和C₂中关于奇点单元的积分为

(15)

在极坐标系下，式(15)中关于A¹ _m的积分为

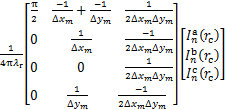(16)

式中：；；；。

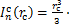
根据式(13)，区域A² _m的y取值范围Y(ξ)在局坐标系下为

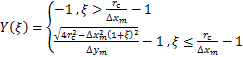(17)

对式(15)关于A² _m的积分进行高斯数值计算^[15]：

(18)

对于矩阵C₁和C₂在其他包含奇点单元的积分，可以采用上述类似的方法计算。

2.3.2　关于线热源的积分　

把线热源Γ进行F等分，用对节点依次编号。根据Simpson积分，各节点的权重为^[10]

    (19)

把式(19)代入式(7)，则有：

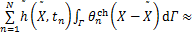
(20)

式中：下标，为曲线节点编号；_f为节点f的坐标；为节点f放热强度。

令

(21)

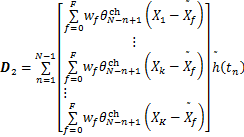(22)

式中：为节点放热强度列向量。

将式(7)应用于裂隙面上的所有节点，则有

(23)

式中：和分别为节点t时刻温度列向量和节点初始温度列向量。

3 数值求解

3.1　有限元方程

令

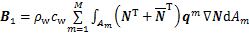(24)

(25)

式中：为单元节点单宽裂隙水流量列向量；为修正系数，用以减小对流占优问题存在的数值振荡。

修正系数为^[16]

(26)

式中：Δx_k为单元沿x_k方向的边长；为单元中心x_k方向的单宽裂隙水流量；k_w为水力扩散率。

对式(1)进行有限元离散（裂隙面网格划分同2.3.1节），则有

(27)

3.2　迭代计算

将式(23)代入式(27)可得

(28)

采用高斯赛德尔迭代计算式(28)（取容差为1%），得到不同时刻的水-岩热交换集度，再代入式(23)，即可求出任意时刻裂隙水和岩石的温度。对于稀疏裂隙岩体系统，亦可采用同样的思路进行求解。

4 算例分析

4.1　方法验证

单一矩形裂隙岩体渗流-传热模型如图5所示，长L、宽W的矩形裂隙沿x-y平面延伸；裂隙水沿x轴方向均匀流动，其入流温度恒为20℃；裂隙水和岩石的初始温度均为90℃；其他参数见表1。当无线热源时，本文采用时域半解析法计算裂隙水温度，与一维解析解^[17]和三维拉氏变换半解析解^[11]作对比以验证该方法的可靠性。选择图5中线段l_f(x=800 m，y=40 m，m)为观察对象，定义量纲一温差为。3种方法的计算结果如图6所示。

表1　计算参数

Table 1　Calculation parameters

由图6可见，时域半解析解与解析解的吻合程度比拉氏变换半解析解的高。原因在于这二种方法的计算格式不同：拉氏变换半解析解需要通过数值逆变换得到时间域上的解答，但数值逆变换存在一定的计算精度问题^[18]；而时域半解析解是时间域上的解答，避免了数值拉氏逆变换过程。因此，时域半解析方法的计算结果更精确，计算过程也更简单。

图5　单一矩形裂隙岩体渗流-传热模型^[11]

Fig. 5　Water flow and heat transfer model in rocks with a rectangular-shaped fracture^[11]

图6　裂隙水的量纲一温差分布

Fig. 6　Normalized water temperature difference distribution in the fracture

4.2　核废处置库近场温度

在图5中，设废物罐线热源沿Γ(x=50~100 m，y=40 m，z=5 m)均匀分布，其放热强度(t)为^[19]

(29)

在衰变热源作用下，观测线l_f的裂隙水温度和l_r(x=0~800 m，y=40 m，z=10 m)的岩石温度分别如图7和图8所示，图中热源温差表示有热源和无热源2种工况时温度的差值。由图7和图8可见，裂隙水和岩石的温度曲线都往裂隙水流方向倾斜，即上游热量经裂隙水传输至下游，加快了核废处置库近场热量向远场传递。由于废物罐的放热功率不断减小，裂隙水和岩石的温度增幅都随时间的推进而降低。

图7　裂隙水温度随衰变热源的变化

Fig. 7　Change of water temperature with varying heat source

图8　岩石温度随衰变热源的变化

Fig. 8　Change of rock temperature with varying heat source

4.3　增强型地热系统温度

将单裂隙对井增强型地热概念模型^[20]扩展至图9所示的多裂隙系统，假设岩体中含有M'个完全相同的平行圆状裂隙，回灌井和生产井都穿过每个裂隙的同1条直径，两井关于裂隙圆心对称。

图9　平行圆状裂隙对井地热系统模型

Fig. 9　Dipole-well geothermal model with parallel disc-shaped fractures

根据单一圆状裂隙的水流方程^[20]，图9中每个裂隙的单宽水流量为

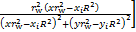(30)

(31)

式中：q_x(X)和q_y(X)分别为x方向和y方向的单宽裂隙水流量；Q_i为作业井的注水量，以注水为正抽水为负，其中i为作业井数；(x_i, y_i) 为i作业井圆心的平面坐标；r_w为作业井半径。

为了分析裂隙空间分布对裂隙水流温度的影响，设注水量Q_in和抽水量Q_ex都为0.05 m³/s，回灌井与生产井的半径都为0.1 m，两井相距60 m，裂隙数为2条，裂隙半径都为50 m，裂隙开度都为0.001 m，3种工况的裂隙间距分别为20，35和50 m，其他参数同表1。由于该系统为对称问题，任一工况裂隙中的水流-传热响应相同。在同步回灌和抽采下，系统运行至10 a时3种工况的裂隙水流温度分布如图10所示。

图10　运行至10 a时3种工况的裂隙水温度分布

Fig. 10　Temperature distributions in different fracture planes at the operation time of 10 years

由图10可见：随着裂隙间距增大，裂隙水流低温区范围逐渐缩小并且收缩速度逐渐下降，这是因为多裂隙内的水-岩热交换过程存在着相互影响，且影响程度与裂隙间距呈负相关。

5 结论

1) 相比于拉氏变换半解析方法，时域半解析方法避免了数值拉氏逆变换及该变换过程存在的误差，具有计算结果更精确和计算过程更简单的特点，还能用于分析含有平行稀疏裂隙岩体的水流-传热，其适用范围更广泛。

2) 裂隙水将上游核废物释放的热量传输至下游，加快了处置库近场热量向远场传递，有利于降低近场温度。因此，对核废处置库近场温度进行预测时，有必要考虑裂隙水流的影响。

参考文献：

[1] 王驹, 陈伟明, 苏锐, 等. 高放废物地质处置及其若干关键科学问题[J]. 岩石力学与工程学报, 2006, 25(4):801-812.

WANG Ju, CHEN Weiming, SU Rui, et al. Geological disposal of high-level radioactive waste and its key scientific issues[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(4): 801-812.

[2] 郭永海, 苏锐, 季瑞利, 等. 高放废物处置库甘肃北山预选区综合水文地质研究[J]. 世界核地质科学, 2014, 31(4): 587-593.

GUO Yonghai, SU Rui, JI Ruili, et al. Synthetic hydrogeological study on Beishan preselected area for high-level radioactive waste repository in China[J]. World Nuclear Geoscience, 2014, 31(4): 587-593.

[3] 张玉军. 核废料处置概念库近场热-水-应力耦合模型及数值分析[J]. 岩土力学, 2007, 28(1): 17-22, 44.

ZHANG Yujun. Coupled thermo-hydro-mechanical model and relevant numerical analysis for near field of conceptual nuclear waste repository[J]. Rock and Soil Mechanics, 2007, 28(1): 17-22, 44.

[4] 张玉军. 核废物地质处置中热-水-应力耦合对迁移影响的三维有限元模拟[J]. 岩土力学, 2009, 30(7): 2126-2132.

ZHANG Yujun. 3D finite element simulation for influence of thermo-hydro-mechanical coupling on migration in geological disposal of nuclear waste[J]. Rock and Soil Mechanics, 2009, 30(7): 2126-2132.

[5] 张玉军, 徐刚, 杨朝帅. 裂隙刚度随应力变化对双重孔隙介质热-水-应力耦合影响的有限元分析[J]. 岩土力学, 2012, 33(11): 3426-3432.

ZHANG Yujun, XU Gang, YANG Chaoshuai. Finite element analysis of influence of fracture stiffness changing with stress on thermo-hydro-mechanical coupling in dual-porosity medium[J]. Rock and Soil Mechanics, 2012, 33(11): 3426-3432.

[6] 柴军瑞. 混凝土坝渗流场与稳定温度场耦合分析的数学模型[J]. 水力发电学报, 2000, 19(1):27-35.

CHAI Junrui. On mathematical model for coupled seepage and temperature field in concrete dam[J]. Journal of Hydroelectric Engineering, 2000, 19(1):27-35.

[7] 刘学艳, 项彦勇. 米尺度裂隙岩体模型水流-传热试验的数值模拟分析[J]. 岩土力学, 2012, 33(1): 287-294.

LIU Xueyan, XIANG Yanyong. Numerical modeling of water flow and heat transfer in a meter-scale physical model of fractured rocks[J]. Rock and Soil Mechanics, 2012, 33(1): 287-294.

[8] 王如宾, 柴军瑞, 陈兴周, 等. 单裂隙水流稳定温度场理论分析[J]. 人民黄河, 2006, 28(5):17-19.

WANG Rubin, CHAI Junrui, CHEN Xingzhou, et al. Analysis of steady temperature field of single fracture flow[J]. Yellow River, 2006, 28(5):17-19.

[9] 王如宾, 柴军瑞. 单裂隙水流作用下岩体稳定温度场理论模型与有限元数值模拟[J]. 水利水电技术, 2006, 37(9):17-19.

WANG Rubin, CHAI Junrui. Theoretical model of rock mass steady temperature field under single fissure flow and numerical simulation with finite element method[J]. Water Resources and Hydropower Engineering, 2006, 37(9):17-19.

[10] 项彦勇, 郭家奇. 分布热源作用下裂隙岩体渗流-传热的拉氏变换-格林函数半解析计算方法[J]. 岩土力学, 2011, 32(2): 333-340.

XIANG Yanyong, GUO Jiaqi. A Laplace transform and Green function method for calculation of water flow and heat transfer in fractured rocks[J]. Rock and Soil Mechanics, 2011, 32(2): 333-340.

[11] 张勇, 项彦勇. 分布热源作用下单裂隙岩体三维水流-传热的半解析计算方法[J]. 岩土力学, 2013, 34(3): 685-695.

ZHANG Yong, XIANG Yanyong. A semi-analytical method for calculation of three-dimensional water flow and heat transfer in single-fracture rock with distributed heat sources[J]. Rock and Soil Mechanics, 2013, 34(3): 685-695.

[12] 张勇, 项彦勇.饱和稀疏裂隙岩体三维水流-传热过程中位移和应力的一种半解析计算方法[J].岩土力学, 2016, 37(12):3481-3490.

ZHANG Yong, XIANG Yanyong. A semi-analytical method for calculation of displacement and stress in processes of 3D water flow and heat transfer in a saturated sparsely fractured rock mass[J]. Rock and Soil Mechanics, 2016, 37(12):3481-3490.

[13] GHASSEMI A, ZHOU X. A three-dimensional thermo-poroelastic model for fracture response to injection/extraction in enhanced geothermal systems[J]. Geothermics, 2011, 40(1): 39-49.

[14] 项彦勇. 地下水力学概论[M]. 北京:科学出版社, 2011: 280-281.

XIANG Yanyong. Fundamental theory of groundwater mechanics[M]. Beijing: Science Press, 2011: 280-281.

[15] 梁国平, 周永发. 有限元语言及其应用[M]. 北京:科学出版社, 2013:582-603.

LIANG Guoping, ZHOU Yongfa. Finite element language and its applications[M]. Beijing: Science Press, 2013: 582-603.

[16] BROOKS A N, HUGHES T J R. Streamline upwind/PetrovGalerkin formulations for convection dominated flows with particular emphasis on the incompressible NavierStokes equations[J]. Computer Methods in Applied Mechanics and Engineering, 1982, 32(1/2/3): 199-259.

[17] LAUWERIER H A. The transport of heat in an oil layer caused by the injection of hot fluid[J]. Applied Scientific Research, 1955, 5(2/3): 145-150.

[18] CHENG A H D, SIDAURUK P, ABOUSLEIMAN Y. Approximate inversion of the Laplace transform[J]. The Mathematica Journal, 1994, 4(2): 76-82.

[19] HOKMARK H, CLAESSON J. Use of an analytical solution for calculating temperatures in repository host rock[J]. Engineering Geology, 2005, 81(3): 353-364.

[20] GHASSEMI A, TARASOVS S, CHENG A H D. An integral solution for threedimensional heat extraction from planar fracture in hot dry rock[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27(12): 989–1004.

（编辑 伍锦花）

收稿日期： 2019 -03 -18; 修回日期： 2019 -05 -18

基金项目(Foundation item)：国家自然科学基金资助项目(51378055)；中央高校基本科研业务费专项资金资助项目(2018YJS104) (Project(51378055) supported by the National Natural Science Foundation of China; Project(2018YJS104) supported by the Fundamental Research Funds for the Central Universities)

通信作者：刘东东，博士研究生，从事裂隙岩体多场耦合研究；E-mail：dongliu@bjtu.edu.cn